Decimal
This article has an unclear citation style. (January 2011) |
This article needs additional citations for verification. (January 2011) |
- This article aims to be an accessible introduction. For the mathematical definition, see Decimal representation.
| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
The decimal numeral system (also called base ten or occasionally denary) has ten as its base. It is the numerical base most widely used by modern civilizations.[1][2]
Decimal notation often refers to a base-10 positional notation such as the Hindu-Arabic numeral system; however, it can also be used more generally to refer to non-positional systems such as Roman or Chinese numerals which are also based on powers of ten.
Decimals also refer to decimal fractions, either separately or in contrast to vulgar fractions. In this context, a decimal is a tenth part, and decimals become a series of nested tenths. There was a notation in use like 'tenth-metre', meaning the tenth decimal of the metre, currently an Angstrom. The contrast here is between decimals and vulgar fractions, and decimal divisions and other divisions of measures, like the inch. It is possible to follow a decimal expansion with a vulgar fraction; this is done with the recent divisions of the troy ounce, which has three places of decimals, followed by a trinary place.
Decimal notation
Decimal notation is the writing of numbers in a base-10 numeral system. Examples are Roman numerals, Brahmi numerals, and Chinese numerals, as well as the Hindu-Arabic numerals used by speakers of many European languages. Roman numerals have symbols for the decimal powers (1, 10, 100, 1000) and secondary symbols for half these values (5, 50, 500). Brahmi numerals have symbols for the nine numbers 1–9, the nine decades 10–90, plus a symbol for 100 and another for 1000. Chinese numerals have symbols for 1–9, and fourteen additional symbols for higher powers of 10, which in modern usage reach 1044.
However, when people who use Hindu-Arabic numerals speak of decimal notation, they often mean not just decimal numeration, as above, but also decimal fractions, all conveyed as part of a positional system. Positional decimal systems include a zero and use symbols (called digits) for the ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent any number, no matter how large or how small. These digits are often used with a decimal separator which indicates the start of a fractional part, and with a symbol such as the plus sign + (for positive) or minus sign − (for negative) adjacent to the numeral to indicate whether it is greater or less than zero, respectively.
Positional notation uses positions for each power of ten: units, tens, hundreds, thousands, etc. The position of each digit within a number denotes the multiplier (power of ten) multiplied with that digit—each position has a value ten times that of the position to its right. There were at least two independent sources of positional decimal systems in ancient civilization: the Chinese counting rod system and the Hindu-Arabic numeral system (the latter descended from Brahmi numerals).
Ten is the number which is the count of fingers and thumbs on both hands (or toes on the feet). The English word digit as well as its translation in many languages is also the anatomical term for fingers and toes. In English, decimal (decimus < Lat.) means tenth, decimate means reduce by a tenth, and denary (denarius < Lat.) means the unit of ten.
The symbols for the digits in common use around the globe today are called Arabic numerals by Europeans and Indian numerals by Arabs, the two groups' terms both referring to the culture from which they learned the system. However, the symbols used in different areas are not identical; for instance, Western Arabic numerals (from which the European numerals are derived) differ from the forms used by other Arab cultures.
Decimal fractions
A decimal fraction is a fraction whose denominator is a power of ten.
Decimal fractions are commonly expressed without a denominator, the decimal separator being inserted into the numerator (with leading zeros added if needed) at the position from the right corresponding to the power of ten of the denominator; e.g., 8/10, 83/100, 83/1000, and 8/10000 are expressed as 0.8, 0.83, 0.083, and 0.0008. In English-speaking and many Asian countries, a period (.) or raised period (·) is used as the decimal separator; in many other countries, a comma is used.
The integer part or integral part of a decimal number is the part to the left of the decimal separator (see also truncation). The part from the decimal separator to the right is the fractional part; if considered as a separate number, a zero is often written in front. Especially for negative numbers, we have to distinguish between the fractional part of the notation and the fractional part of the number itself, because the latter gets its own decimal sign. It is usual for a decimal number whose absolute value is less than one to have a leading zero.
Trailing zeros after the decimal point are not necessary, although in science, engineering and statistics they can be retained to indicate a required precision or to show a level of confidence in the accuracy of the number: Although 0.080 and 0.08 are numerically equal, in engineering 0.080 suggests a measurement with an error of up to one part in two thousand (±0.0005), while 0.08 suggests a measurement with an error of up to one in two hundred (see significant figures).
Other rational numbers
Any rational number with a denominator whose only prime factors are 2 and/or 5 may be precisely expressed as a decimal fraction and has a finite decimal expansion.[3]
- 1/2 = 0.5
- 1/20 = 0.05
- 1/5 = 0.2
- 1/50 = 0.02
- 1/4 = 0.25
- 1/40 = 0.025
- 1/25 = 0.04
- 1/8 = 0.125
- 1/125= 0.008
- 1/10 = 0.1
If the rational number's denominator has any prime factors other than 2 or 5, it cannot be expressed as a finite decimal fraction,[3] and has a unique infinite decimal expansion ending with recurring decimals.
- 1/3 = 0.333333… (with 3 repeating)
- 1/9 = 0.111111… (with 1 repeating)
100-1=99=9×11
- 1/11 = 0.090909… (with 09 repeating)
1000-1=9×111=27×37
- 1/27 = 0.037037037…
- 1/37 = 0.027027027…
- 1/111 = 0 .009009009…
also:
- 1/81= 0.012345679012… (with 012345679 repeating)
Other prime factors in the denominator will give longer recurring sequences; see for instance 1/7, and 1/13.
That a rational number must have a finite or recurring decimal expansion can be seen to be a consequence of the long division algorithm, in that there are only q-1 possible nonzero remainders on division by q, so that the recurring pattern will have a period less than q. For instance, to find 3/7 by long division:
0.4 2 8 5 7 1 4 ...
7 ) 3.0 0 0 0 0 0 0 0
2 8 30/7 = 4 r 2
2 0
1 4 20/7 = 2 r 6
6 0
5 6 60/7 = 8 r 4
4 0
3 5 40/7 = 5 r 5
5 0
4 9 50/7 = 7 r 1
1 0
7 10/7 = 1 r 3
3 0
2 8 30/7 = 4 r 2
2 0
etc.
The converse to this observation is that every recurring decimal represents a rational number p/q. This is a consequence of the fact the recurring part of a decimal representation is, in fact, an infinite geometric series which will sum to a rational number. For instance,
Real numbers
Every real number has a (possibly infinite) decimal representation; i.e., it can be written as
where
- sign() is the sign function, and
- ai ∈ { 0,1,…,9 } for all i ∈ Z are its decimal digits, equal to zero for all i greater than some number (that number being the common logarithm of |x|).
Such a sum converges as i increases, even if there are infinitely many non-zero ai.
Rational numbers (e.g., p/q) with prime factors in the denominator other than 2 and 5 (when reduced to simplest terms) have a unique recurring decimal representation.
Non-uniqueness of decimal representation
Consider those rational numbers which have only the factors 2 and 5 in the denominator, i.e., which can be written as p/(2a5b). In this case there is a terminating decimal representation. For instance, 1/1 = 1, 1/2 = 0.5, 3/5 = 0.6, 3/25 = 0.12 and 1306/1250 = 1.0448. Such numbers are the only real numbers which do not have a unique decimal representation, as they can also be written as a representation that has a recurring 9, for instance 1 = 0.99999…, 1/2 = 0.499999…, etc. The number 0 = 0/1 is special in that it has no representation with recurring 9.
This leaves the irrational numbers. They also have unique infinite decimal representations, and can be characterised as the numbers whose decimal representations neither terminate nor recur.
So in general the decimal representation is unique, if one excludes representations that end in a recurring 9.
The same trichotomy holds for other base-n positional numeral systems:
- Terminating representation: rational where the denominator divides some nk
- Recurring representation: other rational
- Non-terminating, non-recurring representation: irrational
A version of this even holds for irrational-base numeration systems, such as golden mean base representation.
Decimal computation
Decimal computation was carried out in ancient times in many ways, typically on sand tables or with a variety of abaci.
Modern computer hardware and software systems commonly use a binary representation internally (although many early computers, such as the ENIAC or the IBM 650, used decimal representation internally).[4] For external use by computer specialists, this binary representation is sometimes presented in the related octal or hexadecimal systems.
For most purposes, however, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; computer programs express literals in decimal by default. (123.1, for example, is written as such in a computer program, even though many computer languages are unable to encode that number precisely.)
Both computer hardware and software also use internal representations which are effectively decimal for storing decimal values and doing arithmetic. Often this arithmetic is done on data which are encoded using some variant of binary-coded decimal,[5] especially in database implementations, but there are other decimal representations in use (such as in the new IEEE 754 Standard for Floating-Point Arithmetic).[6]
Decimal arithmetic is used in computers so that decimal fractional results can be computed exactly, which is not possible using a binary fractional representation. This is often important for financial and other calculations.[7]
History
History of positional decimal system in China

Upper row vertical form
Lower row horizontal form
The earliest evidence of positional numeral system appeared in 13th century B.C in Shang dynasty in China, and it was more advanced[clarification needed] than contemporary Babylon and Egypt[8]
- In 1913, noted Japanese mathematics historian Yoshio Mikami wrote that counting rods were used since the year 542 BC. Counting rods (Y.Mikami called them "calculating pieces") are made of bamboo or wooden pieces of red and black colors, the red pieces representing positive numbers, and the black for negative numbers.[9] Archaeological evidence indicated that a full-fledged, positional decimal system of numerals, known as the rod calculus, consisting of "hardware" (the counting rods) and "software" (Chinese multiplication table) with the associated arithmetic operations of addition, subtraction, multiplication and division was fully developed in theSpring and Autumn period,[10] Artifacts include forty Spring and Autumn period bamboo calculating rods of 12 inch each from Hunan Chang Sha Zhuo Gong mountain area, and a bundle of well preserved animal bone calculating rods stored in a silk pouch, unearthed from a West Han era tomb from Shanxi Qian Yang county. Most importantly, in 2002, Chinese archaeologists unearthed a wood script from a two-thousand-year-old site from the Warring States period, on which is written "four eight thirty two, five eight forty, six eight forty eight." This is the earliest discovered instance of a Chinese multiplication table, which is a prerequisite piece of "software" for carrying out positional decimal calculation with counting rods. Unlike the multiplication tables of other civilizations, the Chinese multiplication table in use since the Warring States contains at most 81 terms, from 9x9 to 1x1, consistent with a positional decimal rod calculus system. A non positional decimal system would require a much larger multiplication table. Chinese artifacts never evidence the need for a multiplication table larger the 9x9 terms from the antiquity of rod calculus to the era of the abacus.
- Joseph Needham writes: "The Shang Chinese system, seems, then, the simplest of the ancient methods, and appeared two thousand years before the West inherited what are usually called the 'Arabic' numerals."[11]
Invention of positional decimal zero
There is no special counting rod symbol for decimal zero, the Chinese had no need for it, as null, or nothing is the natural result of subtraction, intrinsic to rod calculus, it is a blank position on the counting board. For instance subtract 2 from 32 (32 -2) is carried out on the board as: layout 三|| on the counting board, left hand side has higher rank than the right, literally take away 2 rods from the first position resulting in a blank in the first position, the result was "三BLANK",meaning 30. The "blank" on counting board was the symbol for zero.
In short, full fledged positional decimal numerals in the form of counting rods was in use more than one millennium before the advent of Hindu-Arabic numerals. This gave the Chinese great advantage in computation, for instance Zu Chongzhi obtained the most accurate approximation for π for over nine hundred years. . However, Zu Chongzhi did not calculate π at all, but arrived to the value by the same geometric method which the Greek polymath Archimedes had used centuries earlier in the first known computation of pi.[12]
China was the earliest civilization to adopt the concept of Hindu-Arabic numeral system[13]
Abacus

Rod calculus was the computing mechanism in China from antiquity up to Ming dynasty, when it was replaced by the more portable and much quicker abacus. However, the abacus retains all the main feature of counting rods, a rod became a bead, an overhead rod became an overhead bead top of a partion bar, there is exact 1 to 1 correspondence between a rod numeral and abacus numeral, In a sense, the counting rods mutated into abacus, in other words, the ancient Chinese positional decimal system took a new form and lives on in abacus. Like the counting rods, a blank on a position on abacus represents 0.
Possible Chinese origin of Hindu–Arabic numeral system

10th century Kushyar ibn Labban division, a replica of 5th century Sunsi division

[14]

Khwarizmi division of 825AD, completely identical to Sun Zi division algorithm
[15]
Comparison of the computation in Kitab al-Fusul fi al-Hisab al Hindi (925) by al-Uqlidisi, and another Latin translation of Arab manuscript written by the Persian mathematician Khwarizmi (825), uncovered almost identical algorithm for multiplication and division with the rod calculus described in Mathematical Classic of Sun Zi.[16]In the case of division, the algorithm described by Khwarizmi and algorithm described by Sun Zi four hundred years earlier, are completely identical to the last detail: exactly the same three tier layout, exactly the same assignemt of dividend to the middle row, the same assignment of smaller divisor to the bottom row, padded with blank(!) but not "0" to the right, and quotient to top row padded with blanks(!) but not "0"s;identical alignment of the most significant digit, exactly the same way of calculating from left to right, exactly the same way of shifting divisor to the right one position after each step, up to presentation of the remainder in the form of counting rod fraction.[17]Too identical to explained with independent development, further moving material rods on counting board to the right is a simple matter, on the other hand, moving written numbers right one step at each stage "is not conducive to a written system", as Lam Lay Yong put it[18]
10th century Persian mathematician Kushyar ibn Labban's division algorithm described in his book Principles of Hindu Reckoning is also identical to Sunzi division 500 hundred years earlier.[19] The similarity between ibn Labban's square root algorithm and Sunzi's square root algorithm is also "striking".[20]
Historian of mathematic Lam Lay Yong suggests that "The fact that Arabs and the Chinese had identical expression of fractions, identical arithmetic procedures and identical expression of numerals cannot be dismissed as mere coincidence. Given that the Chinese had evolved all these forms and procedures at a significant earlier date, this inevitably points to the Chinese origin of the Hindu Arabic numeral system."[21]
History of the Hindu-Arabic numeral system
Georges Ifrah claims that the modern numeral system format, known as the Hindu-Arabic numeral system, originated in Indian mathematics by the 5th century CE.[22] In the Lokavibhâga (The Parts of the Universe) uses both a concept of zero and also the place-value system. For example, "pañchabhyah khalu shûnyebhyah param dve sapta châmbaram ekam trîni cha rûpam cha" ("five voids, then two and seven, the sky, one and three and the form") is the expression of the number 13,107,200,000. This document, can be dated to the mid 5th century CE and is the oldest known Indian document to use these concepts.[23] According to this theory, the ideas were transmitted to Chinese mathematics and Islamic mathematics during and after that time.[24] It was notably introduced to the west through Khwārizmī's On the Calculation with Hindu Numerals.
History of decimal fractions
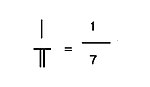
According to Joseph Needham, decimal fractions were first developed and used by the Chinese in the 1st century BC, and then spread to the Middle East and from there to Europe.[25] The written Chinese decimal fractions were non-positional.[25] However, counting rod fractions were positional.
Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by
- 寸
- 096644
Immanuel Bonfils invented decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them.[27]
The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century, though J. Lennart Berggren notes that positional decimal fractions were used five centuries before him by Arab mathematician Abu'l-Hasan al-Uqlidisi as early as the 10th century.[28]
Khwarizmi introducted fraction to Islamic countries in the early 9th century, his fraction presentation was taken from traditional Chinese mathematical fraction. This form of fraction with numerator on top and denomiator at bottom without a horizontal bar was also used by 10th century Abu'l-Hasan al-Uqlidisi and 15th century Jamshīd al-Kāshī's work "Arithmetic Key".
A forerunner of modern European decimal notation was introduced by Simon Stevin in the 16th century.[29]
Natural languages
A straightforward decimal rank system with a word for each order 10十,100百,1000千,10000万, and in which 11 is expressed as ten-one and 23 as two-ten-three, and 89345 is expressed as 8万9千3百4十5 is found in Chinese languages, and in Vietnamese with a few irregularities. Japanese, Korean, and Thai have imported the Chinese decimal system. Many other languages with a decimal system have special words for the numbers between 10 and 20, and decades. For example in English 11 is "eleven" not "ten-one".
Incan languages such as Quechua and Aymara have an almost straightforward decimal system, in which 11 is expressed as ten with one and 23 as two-ten with three.
Some psychologists suggest irregularities of the English names of numerals may hinder children's counting ability.[30]
Alternative bases
Some cultures do, or did, use other numeral systems, most notably
- pre-Columbian Mesoamerican cultures such as the Maya used a base 20 system (using all twenty fingers and toes) and
- the Babylonians used base 60.
In addition, it has been suggested that many other cultures developed alternative numeral systems (although the extent is debated):
- Many or all of the Chumashan languages originally used a base 4 counting system, in which the names for numbers were structured according to multiples of 4 and 16.[31]
- Many languages[32] use quinary number systems, including Gumatj, Nunggubuyu,[33] Kuurn Kopan Noot[34] and Saraveca. Of these, Gumatj is the only true "5-25" language known, in which 25 is the higher group of 5.
- Some Nigerians use base 12 systems[citation needed]
- The Huli language of Papua New Guinea is reported to have base 15 numerals.[35] Ngui means 15, ngui ki means 15×2 = 30, and ngui ngui means 15×15 = 225.
- Umbu-Ungu, also known as Kakoli, is reported to have base-24 numerals.[36][37] Tokapu means 24, tokapu talu means 24×2 = 48, and tokapu tokapu means 24×24 = 576.
- Base 27 is used in two natural languages, the Telefol language and the Oksapmin language of Papua New Guinea.[citation needed]
- Ngiti is reported to have a base 32 numeral system with base 4 cycles.[38]
See also
References
- ^ The History of Arithmetic, Louis Charles Karpinski, 200pp, Rand McNally & Company, 1925.
- ^ Histoire universelle des chiffres, Georges Ifrah, Robert Laffont, 1994 (Also: The Universal History of Numbers: From prehistory to the invention of the computer, Georges Ifrah, ISBN 0471393401, John Wiley and Sons Inc., New York, 2000. Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk)
- ^ a b Math Made Nice-n-Easy. Piscataway, N.J.: Research Education Association. 1999. p. 141. ISBN 0-87891-200-2.
- ^ Fingers or Fists? (The Choice of Decimal or Binary Representation), Werner Buchholz, Communications of the ACM, Vol. 2 #12, pp3–11, ACM Press, December 1959.
- ^ Decimal Computation, Hermann Schmid, John Wiley & Sons 1974 (ISBN 047176180X); reprinted in 1983 by Robert E. Krieger Publishing Company (ISBN 0898743184)
- ^ Decimal Floating-Point: Algorism for Computers, Cowlishaw, M. F., Proceedings 16th IEEE Symposium on Computer Arithmetic, ISBN 0-7695-1894-X, pp104-111, IEEE Comp. Soc., June 2003
- ^ Decimal Arithmetic - FAQ
- ^ Colin Ronan, The Shorter Science and Civilication in China, An Abridgement of Joseph Needham's original text, vol II, page 5
- ^ Yoshio Mikami, History of Mathematics in China and Japan, p27. Chelsea, New York
- ^ Wu Wen Jun ed The Grand Series of History of Chinese Mathematics, Vol I, p365-384
- ^ Colin A. Ronan and Joseph Needham, The Shorter Science & Civilization in China vol 2, Cambridge University Press, pp 5–6
- ^ David H. Bailey, Jonathan M. Borwein, Peter B. Borwein, Simon Plouffe: “The Quest for Pi”, Mathematical Intelligencer, Vol. 19, No. 1 (1997), pp. 50–57 (50f.)
- ^ Lam Lay Yong, A Chinese Genesis, Rewriting the history of our numeral system. Archive for History of Exact Sciences 38, 101-108.
- ^ Lam Lay Yong: "The Development of Hindu-Arabic and Traditional Chinese Arithmetic", Chinese Science 13 (1996) p45 diagram i to viii
- ^ Lam Lay Yong, "The Development of Hindu-Arabic and Traditional Chinese Arithmetic", Chinese Science, 1996 p38, Kurt Vogel notation
- ^ Lam Lay Yong, Fleeting Footsteps, p141
- ^ Lam Lay Yong, An Tian Se, Fleeting Footsteps, p42-44
- ^ Lam Lay Yong, Ang Tian Se, Fleeting Footsteps, p143 ISBN 981-02-3696-4
- ^ Lam Lay Yong, Ang Tian Se, Fleeting Footsteps, p44, diagram i thru v ISBN 981-02-3696-4
- ^ Lam Lay Yong, ibid ISBN 981-02-3696-4
- ^ Lam Lay Yong, Ang Tian Se, Fleeting Footsteps, Tracing the Conception of Arithmetic and Algebra in Ancient China ISBN 981-02-3696-4
- ^ Ifrah, p. 346
- ^ Ifrah, p.416
- ^ Britannica Concise Encyclopædia (2007). algebra
- ^ a b Joseph Needham (1959). "Decimal System". Science and Civilisation in China, Volume III, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press.
- ^ Jean-Claude Martzloff, A History of Chinesse Mathematics, Springer 1997 ISBN 3-540-33782-2
- ^ Gandz, S.: The invention of the decimal fractions and the application of the exponential calculus by Immanuel Bonfils of Tarascon (c. 1350), Isis 25 (1936), 16–45.
- ^ Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 518. ISBN 9780691114859.
- ^ B. L. van der Waerden (1985). A History of Algebra. From Khwarizmi to Emmy Noether. Berlin: Springer-Verlag.
- ^ Azar, Beth (1999). "English words may hinder math skills development". American Psychology Association Monitor. 30 (4). Archived from the original on 2007-10-21.
- ^ There is a surviving list of Ventureño language number words up to 32 written down by a Spanish priest ca. 1819. "Chumashan Numerals" by Madison S. Beeler, in Native American Mathematics, edited by Michael P. Closs (1986), ISBN 0-292-75531-7.
- ^ Harald Hammarström, Rarities in Numeral Systems: "Bases 5, 10, and 20 are omnipresent."
- ^ Harris, John (1982). Hargrave, Susanne (ed.). Facts and fallacies of aboriginal number systems (PDF). Vol. 8. pp. 153–181.
{{cite book}}:|journal=ignored (help) - ^ Dawson, J. "Australian Aborigines: The Languages and Customs of Several Tribes of Aborigines in the Western District of Victoria (1881), p. xcviii.
- ^ Cheetham, Brian (1978). "Counting and Number in Huli". Papua New Guinea Journal of Education. 14: 16–35.
- ^ Gordon, Raymond G., Jr., ed. (2005). "Umbu-Ungu". Ethnologue: Languages of the World (15 ed.). Retrieved 2008-03-16.
{{cite book}}: CS1 maint: multiple names: editors list (link) - ^ Bowers, Nancy; Lepi, Pundia (1975). "Kaugel Valley systems of reckoning" (PDF). Journal of the Polynesian Society. 84 (3): 309–324.
- ^ Hammarström, Harald (2006). "Proceedings of Rara & Rarissima Conference" (PDF).
{{cite web}}:|contribution=ignored (help)





