Elongated triangular cupola

Elongated triangular cupola
Type	Johnson J17 - J18 - J19
Faces	1+3 triangles 3x3 squares 1 hexagon
Edges	27
Vertices	15
Vertex configuration	6(42.6) 3(3.4.3.4) 6(3.43)
Symmetry group	C3v
Dual polyhedron	-
Properties	convex
Net

In geometry, the elongated triangular cupola is one of the Johnson solids (J₁₈). As the name suggests, it can be constructed by elongating a triangular cupola (J₃) by attaching a hexagonal prism to its base.

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.

Formulae

The following formulae for volume and surface area can be used if all faces are regular, with edge length a:

$V=({\frac {1}{6}}(5{\sqrt {2}}+9{\sqrt {3}}))a^{3}\approx 3.77659...a^{3}$

$A=(9+{\frac {5{\sqrt {3}}}{2}})a^{2}\approx 13.3301...a^{2}$

Dual polyhedron

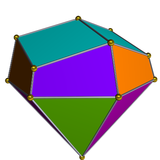
The dual of the elongated triangular cupola has 15 faces: 6 isosceles triangles, 3 rhombi, and 6 quadrilaterals.

Dual elongated triangular cupola	Net of dual

Related polyhedra and honeycombs

The elongated triangular cupola can form a tessellation of space with tetrahedra and square pyramids.

External links

• Weisstein, Eric W., "Elongated triangular cupola" ("Johnson solid") at MathWorld.