List of numeral systems
Appearance
| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
This is a list of numeral systems, that is, writing systems for expressing numbers.
By culture
| Name | Base | Sample | Approx. first appearance | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Babylonian numerals | 60 | 3100 BC | |||||||||||||||||
| Egyptian numerals | 10 |
or
|
3000 BC | ||||||||||||||||
| Aegean numerals | 10 | 𐄇 𐄈 𐄉 𐄊 𐄋 𐄌 𐄍 𐄎 𐄏 𐄐 𐄑 𐄒 𐄓 𐄔 𐄕 𐄖 𐄗 𐄘 𐄙 𐄚 𐄛 𐄜 𐄝 𐄞 𐄟 𐄠 𐄡 𐄢 𐄣 𐄤 𐄥 𐄦 𐄧 𐄨 𐄩 𐄪 𐄫 𐄬 𐄭 𐄮 𐄯 𐄰 𐄱 𐄲 𐄳 |
c1500 BC | ||||||||||||||||
| Maya numerals | 20 | <15th century | |||||||||||||||||
| Muisca numerals | 20 |  |
<15th century | ||||||||||||||||
| Indian Numerals | 10 | Tamil ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯
Devanagari 0 १ २ ३ ४ ५ ६ ७ ८ ९ |
750 BC – 690 BC | ||||||||||||||||
| Chinese numerals, Japanese numerals, Korean numerals (Sino-Korean) | 10 | 〇/零 一 二 三 四 五 六 七 八 九 十 | |||||||||||||||||
| Chinese rod numerals | 10 | 𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩 | 1st century | ||||||||||||||||
| Roman numerals | 10 | N Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ L C D M |
1000 BC | ||||||||||||||||
| Greek numerals | 10 | ō α β γ δ ε ϝ ζ η θ ι ο Αʹ Βʹ Γʹ Δʹ Εʹ Ϛʹ Ζʹ Ηʹ Θʹ |
Before 5th century BC | ||||||||||||||||
| Western Arabic numerals | 10 | 0 1 2 3 4 5 6 7 8 9 | 9th century | ||||||||||||||||
| Thai numerals | 10 | ๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙ | |||||||||||||||||
| John Napier's Location arithmetic | 2 | a b ab c ac bc abc d ad bd abd cd acd bcd abcd | 1617 in Rabdology, a non-positional binary system | ||||||||||||||||
| Hebrew numerals | 10 | א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ |
800 BC | ||||||||||||||||
| Abjad numerals | 10 | غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا |
By type of notation
Numeral systems are classified here as to whether they use positional notation (also known as place-value notation), and further categorized by radix or base.
Standard positional numeral systems
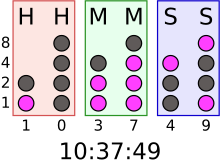
The common names are derived somewhat arbitrarily from a mix of Latin and Greek, in some cases including roots from both languages within a single name.[1]
| Base | Name | Usage |
|---|---|---|
| 2 | Binary | Digital computing |
| 3 | Ternary | Cantor set (all points in [0,1] that can be represented in ternary with no 1s); counting Tasbih in Islam; hand-foot-yard and teaspoon-tablespoon-shot measurement systems; most economical integer base |
| 4 | Quaternary | Data transmission and Hilbert curves; Chumashan languages, and Kharosthi numerals |
| 5 | Quinary | Gumatj, Nunggubuyu, Kuurn Kopan Noot, and Saraveca languages; common count grouping e.g. tally marks |
| 6 | Senary | Diceware, Ndom, Kanum, and Proto-Uralic language (suspected) |
| 8 | Octal | Charles XII of Sweden, Unix-like permissions, Squawk codes, DEC PDP-11, compact notation for binary numbers, Xiantian (I Ching, China) |
| 10 | Decimal | Most widely used by modern civilizations[2][3][4] |
| 11 | Undecimal | Jokingly proposed during the French Revolution to settle a dispute between those proposing a shift to duodecimal and those who were content with decimal |
| 12 | Duodecimal | Languages in the Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, and the Nimbia dialect of Gwandara; Chepang language of Nepal, and the Mahl dialect of Maldivian; dozen-gross-great gross counting; hours and months timekeeping; years of Chinese zodiac; foot and inch. |
| 13 | Tridecimal | Conway base 13 function |
| 14 | Tetradecimal | Programming for the HP 9100A/B calculator[5] and image processing applications[6] |
| 15 | Pentadecimal | Telephony routing over IP, and the Huli language |
| 16 | Hexadecimal | Base16 encoding; compact notation for binary data; tonal system |
| 20 | Vigesimal | Basque, Celtic, Maya, Muisca, Inuit, Yoruba, Tlingit, and Dzongkha numerals; Santali, and Ainu languages |
| 24 | Tetravigesimal | Kaugel language |
| 26 | Hexavigesimal | Base 26 encoding; sometimes used for encryption or ciphering.[7] |
| 27 | Heptavigesimal | Mapping the nonzero digits to the alphabet and zero to the space is occasionally used to provide checksums for alphabetic data such as personal names,[8] to provide a concise encoding of alphabetic strings,[9] or as the basis for a form of gematria.[10] |
| 30 | Trigesimal | The Natural Area Code |
| 32 | Duotrigesimal | Base32 encoding and the Ngiti language |
| 36 | Hexatrigesimal | Base36 encoding; use of letters with digits |
| 52 | Duoquinquagesimal | Base52 encoding, a variant of Base62 without vowels[11] |
| 56 | Hexaquinquagesimal | Base56 encoding, a variant of Base58[12] |
| 57 | Heptaquinquagesimal | Base57 encoding, a variant of Base62 excluding I, O, l, U, and u[13] |
| 58 | Octoquinquagesimal | Base58 encoding |
| 60 | Sexagesimal | Babylonian numerals; NewBase60 encoding, similar to Base62, excluding I, O, and l, but including _(underscore);[14] degrees-minutes-seconds and hours-minutes-seconds measurement systems; Ekari and Sumerian languages |
| 61 | Unsexagesimal | NewBase61 encoding, variant of NewBase60 with a space[15] |
| 62 | Duosexagesimal | Base62 encoding, using 0-9, A-Z, and a-z |
| 64 | Tetrasexagesimal | Base64 encoding, , I Ching in China |
| 65 | Pentasexagesimal | Base65 encoding, a variant of Base64[16] |
| 85 | Pentoctogesimal | Ascii85 encoding. This is the minimum number of characters needed to encode a 32 bit number into 5 printable characters in a process similar to MIME-64 encoding, since 855 is only slightly bigger than 232. Such method is 6.7% more efficient than MIME-64 which encodes a 24 bit number into 4 printable characters. |
| 91 | Unnonagesimal | Base91 encoding, using all ASCII except "-" (0x2D), "\" (0x5C), and "'" (0x27); one variant uses "\" (0x5C) in place of """ (0x22). |
| 92 | Duononagesimal | Base92 encoding, using all of ASCII except for "`" (0x60) and """ (0x22) due to confusability.[17] |
| 94 | Tetranonagesimal | Base94 encoding, using all of ASCII printable characters.[18] |
| 95 | Pentanonagesimal | Base95 encoding, a variant of Base94 with the addition of the Space character.[19] |
| 256 | Ducentahexaquinquagesimal | Base256 encoding, Ifá, Nigeria |
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base-1) | Tally marks |
| 10 | Bijective base-10 | |
| 26 | Bijective base-26 | Spreadsheet column numeration. Also used by John Nash as part of his obsession with numerology and the uncovering of "hidden" messages.[20] |
| Base | Name | Usage |
|---|---|---|
| 2 | Balanced binary (Non-adjacent form) | |
| 3 | Balanced ternary | Ternary computers |
| 5 | Balanced quinary | |
| 9 | Balanced nonary | |
| 10 | Balanced decimal | John Colson Augustin Cauchy |
The common names of the negative base numeral systems are formed using the prefix nega-, giving names such as:
| Base | Name | Usage |
|---|---|---|
| −2 | Negabinary | |
| −3 | Negaternary | |
| −10 | Negadecimal |
| Base | Name | Usage |
|---|---|---|
| 2i | Quater-imaginary base | |
| −1 ± i | Twindragon base | Twindragon fractal shape |
| Base | Name | Usage |
|---|---|---|
| φ | Golden ratio base | Early Beta encoder[21] |
| e | Base | Lowest radix economy |
Other
Non-positional notation
All known numeral systems developed before the Babylonian numerals are non-positional.[22]
Trivia
- In this Youtube video, Matt Parker jokingly invented a base-1082 system (From a Fermi estimate of the number of atoms in the universe). He uses this numeral system to describe how many atom carry-overs (i.e. number of parallel universes, or digits in this radix) it takes to have a hypothetical supercomputer generate all possible 256×256 grayscale images, when the root universe lasts 1017 seconds (another Fermi estimate). This turns out to be 1925.
See also
- Radix
- Radix economy
- Table of bases
- List of numbers in various languages (cardinal number names)
- Numeral prefix
References
- ^ For the mixed roots of the word "hexadecimal", see Epp, Susanna (2010), Discrete Mathematics with Applications (4th ed.), Cengage Learning, p. 91, ISBN 9781133168669.
- ^ The History of Arithmetic, Louis Charles Karpinski, 200pp, Rand McNally & Company, 1925.
- ^ Histoire universelle des chiffres, Georges Ifrah, Robert Laffont, 1994.
- ^ The Universal History of Numbers: From prehistory to the invention of the computer, Georges Ifrah, ISBN 0-471-39340-1, John Wiley and Sons Inc., New York, 2000. Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk
- ^ HP Museum
- ^ Free Patents Online
- ^ http://www.dcode.fr/base-26-cipher
- ^ Grannis, Shaun J.; Overhage, J. Marc; McDonald, Clement J. (2002), "Analysis of identifier performance using a deterministic linkage algorithm", Proc AMIA Symp., pp. 305–309, PMC 2244404, PMID 12463836.
- ^ Stephens, Kenneth Rod (1996), Visual Basic Algorithms: A Developer's Sourcebook of Ready-to-run Code, Wiley, p. 215, ISBN 9780471134183.
- ^ Sallows, Lee (1993), "Base 27: the key to a new gematria", Word Ways, 26 (2): 67–77.
- ^ "Base52". Retrieved 2016-01-03.
- ^ "Base56". Retrieved 2016-01-03.
- ^ "Base57". Retrieved 2016-01-03.
- ^ "NewBase60". Retrieved 2016-01-03.
- ^ "NewBase61". Retrieved 2016-01-03.
- ^ "Base65 Encoding". Retrieved 2016-01-03.
- ^ "Base92". Retrieved 2016-01-03.
- ^ "Base94". Retrieved 2016-01-03.
- ^ "base95 Numeric System". Retrieved 2016-01-03.
- ^ Nasar, Sylvia (2001). A Beautiful Mind. Simon and Schuster. pp. 333–6. ISBN 0-7432-2457-4.
- ^ Ward, Rachel (2008), "On Robustness Properties of Beta Encoders and Golden Ratio Encoders", IEEE Transactions on Information Theory, 54 (9): 4324–4334, doi:10.1109/TIT.2008.928235
- ^ Chrisomalis calls the Babylonian system "the first positional system ever" in Chrisomalis, Stephen (2010), Numerical Notation: A Comparative History, Cambridge University Press, p. 254, ISBN 9781139485333.

