Three-phase electric power

Three-phase electric power (abbreviated 3ϕ[1]) is a common type of alternating current (AC) used in electricity generation, transmission, and distribution.[2] It is a type of polyphase system employing three wires (or four including an optional neutral return wire) and is the most common method used by electrical grids worldwide to transfer power.
Three-phase electrical power was developed in the 1880s by several people. In three-phase power, the voltage on each wire is 120 degrees phase shifted relative to each of the other wires. Because it is an AC system, it allows the voltages to be easily stepped up using transformers to high voltage for transmission and back down for distribution, giving high efficiency.
A three-wire three-phase circuit is usually more economical than an equivalent two-wire single-phase circuit at the same line-to-ground voltage because it uses less conductor material to transmit a given amount of electrical power.[3] Three-phase power is mainly used directly to power large induction motors, other electric motors and other heavy loads. Small loads often use only a two-wire single-phase circuit, which may be derived from a three-phase system.
Terminology[edit]
The conductors between a voltage source and a load are called lines, and the voltage between any two lines is called line voltage. The voltage measured between any line and neutral is called phase voltage.[4] For example, for a 208/120-volt service, the line voltage is 208 volts, and the phase voltage is 120 volts.
History[edit]
Polyphase power systems were independently invented by Galileo Ferraris, Mikhail Dolivo-Dobrovolsky, Jonas Wenström, John Hopkinson, William Stanley Jr., and Nikola Tesla in the late 1880s.[5]

Three phase power evolved out of electric motor development. In 1885, Galileo Ferraris was doing research on rotating magnetic fields. Ferraris experimented with different types of asynchronous electric motors. The research and his studies resulted in the development of an alternator, which may be thought of as an alternating-current motor operating in reverse, so as to convert mechanical (rotating) power into electric power (as alternating current). On 11 March 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin.
Two months later Nikola Tesla gained U.S. patent 381,968 for a three-phase electric motor design, application filed October 12, 1887. Figure 13 of this patent shows that Tesla envisaged his three-phase motor being powered from the generator via six wires.
These alternators operated by creating systems of alternating currents displaced from one another in phase by definite amounts, and depended on rotating magnetic fields for their operation. The resulting source of polyphase power soon found widespread acceptance. The invention of the polyphase alternator is key in the history of electrification, as is the power transformer. These inventions enabled power to be transmitted by wires economically over considerable distances. Polyphase power enabled the use of water-power (via hydroelectric generating plants in large dams) in remote places, thereby allowing the mechanical energy of the falling water to be converted to electricity, which then could be fed to an electric motor at any location where mechanical work needed to be done. This versatility sparked the growth of power-transmission network grids on continents around the globe.
Mikhail Dolivo-Dobrovolsky developed a three-phase electrical generator and a three-phase electric motor in 1888 and studied star and delta connections. His three-phase three-wire transmission system was displayed in 1891 in Germany at the International Electrotechnical Exhibition, where Dolivo-Dobrovolsky used the system to transmit electric power at the distance of 176 km (110 miles) with 75% efficiency. In 1891 he also created a three-phase transformer and short-circuited (squirrel-cage) induction motor.[6][7] He designed the world's first three-phase hydroelectric power plant in 1891. Inventor Jonas Wenström received in 1890 a Swedish patent on the same three-phase system.[8] The possibility of transferring electrical power from a waterfall at a distance was explored at the Grängesberg mine. A 45 m fall at Hällsjön, Smedjebackens kommun, where a small iron work had been located, was selected. In 1893, a three-phase 9.5 kv system was used to transfer 400 horsepower a distance of 15 km (10 miles), becoming the first commercial application.[9]
Principle[edit]



In a symmetric three-phase power supply system, three conductors each carry an alternating current of the same frequency and voltage amplitude relative to a common reference, but with a phase difference of one third of a cycle (i.e., 120 degrees out of phase) between each. The common reference is usually connected to ground and often to a current-carrying conductor called the neutral. Due to the phase difference, the voltage on any conductor reaches its peak at one third of a cycle after one of the other conductors and one third of a cycle before the remaining conductor. This phase delay gives constant power transfer to a balanced linear load. It also makes it possible to produce a rotating magnetic field in an electric motor and generate other phase arrangements using transformers (for instance, a two-phase system using a Scott-T transformer). The amplitude of the voltage difference between two phases is times the amplitude of the voltage of the individual phases.
The symmetric three-phase systems described here are simply referred to as three-phase systems because, although it is possible to design and implement asymmetric three-phase power systems (i.e., with unequal voltages or phase shifts), they are not used in practice because they lack the most important advantages of symmetric systems.
In a three-phase system feeding a balanced and linear load, the sum of the instantaneous currents of the three conductors is zero. In other words, the current in each conductor is equal in magnitude to the sum of the currents in the other two, but with the opposite sign. The return path for the current in any phase conductor is the other two phase conductors.
Constant power transfer is possible with any number of phases greater than one. However, two-phase systems do not have neutral-current cancellation and thus use conductors less efficiently, and more than three phases complicates infrastructure unnecessarily. Additionally, in some practical generators and motors, two phases can result in a less smooth (pulsating) torque. [10]
Three-phase systems may have a fourth wire, common in low-voltage distribution. This is the neutral wire. The neutral allows three separate single-phase supplies to be provided at a constant voltage and is commonly used for supplying multiple single-phase loads. The connections are arranged so that, as far as possible in each group, equal power is drawn from each phase. Further up the distribution system, the currents are usually well balanced. Transformers may be wired to have a four-wire secondary and a three-wire primary, while allowing unbalanced loads and the associated secondary-side neutral currents.
Phase sequence[edit]
Wiring for three phases is typically identified by colors that vary by country and voltage. The phases must be connected in the correct order to achieve the intended direction of rotation of three-phase motors. For example, pumps and fans do not work as intended in reverse. Maintaining the identity of phases is required if two sources could be connected at the same time. A direct connection between two different phases is a short circuit and leads to flow of unbalanced current.
Advantages and disadvantages[edit]
As compared to a single-phase AC power supply that uses two current-carrying conductors (phase and neutral), a three-phase supply with no neutral and the same phase-to-ground voltage and current capacity per phase can transmit three times as much power by using just 1.5 times as many wires (i.e., three instead of two). Thus, the ratio of capacity to conductor material is doubled.[11] The ratio of capacity to conductor material increases to 3:1 with an ungrounded three-phase and center-grounded single-phase system (or 2.25:1 if both use grounds with the same gauge as the conductors). That leads to higher efficiency, lower weight, and cleaner waveforms.
Three-phase supplies have properties that make them desirable in electric power distribution systems:
- The phase currents tend to cancel out one another, summing to zero in the case of a linear balanced load, which allows a reduction of the size of the neutral conductor because it carries little or no current. With a balanced load, all the phase conductors carry the same current and so can have the same size.
- Power transfer into a linear balanced load is constant, which, in motor/generator applications, helps to reduce vibrations.
- Three-phase systems can produce a rotating magnetic field with a specified direction and constant magnitude, which simplifies the design of electric motors, as no starting circuit is required.
However, most loads are single-phase. In North America, single-family houses and individual apartments are supplied one phase from the power grid and use a split-phase system to the panelboard from which most branch circuits will carry 120 V. Circuits designed for higher powered devices such as stoves, dryers, or outlets for electric vehicles carry 240 V.
In Europe, three-phase power is normally delivered to the panelboard and further to higher powered devices.
Generation and distribution[edit]
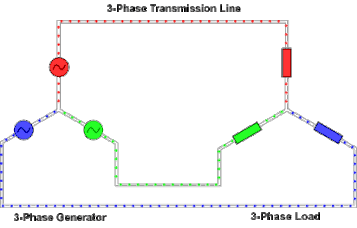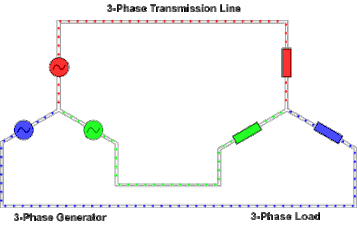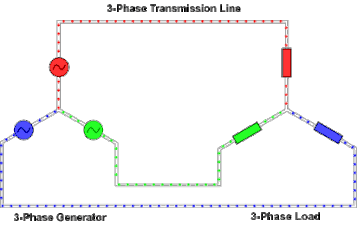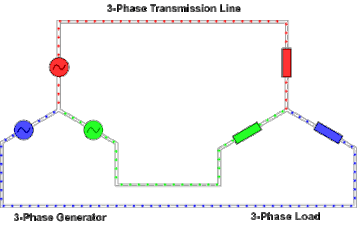
At the power station, an electrical generator converts mechanical power into a set of three AC electric currents, one from each coil (or winding) of the generator. The windings are arranged such that the currents are at the same frequency but with the peaks and troughs of their wave forms offset to provide three complementary currents with a phase separation of one-third cycle (120° or 2π⁄3 radians). The generator frequency is typically 50 or 60 Hz, depending on the country.
At the power station, transformers change the voltage from generators to a level suitable for transmission in order to minimize losses.
After further voltage conversions in the transmission network, the voltage is finally transformed to the standard utilization before power is supplied to customers.
Most automotive alternators generate three-phase AC and rectify it to DC with a diode bridge.[14]
Transformer connections[edit]
A "delta" (Δ) connected transformer winding is connected between phases of a three-phase system. A "wye" (Y) transformer connects each winding from a phase wire to a common neutral point.
A single three-phase transformer can be used, or three single-phase transformers.
In an "open delta" or "V" system, only two transformers are used. A closed delta made of three single-phase transformers can operate as an open delta if one of the transformers has failed or needs to be removed.[15] In open delta, each transformer must carry current for its respective phases as well as current for the third phase, therefore capacity is reduced to 87%. With one of three transformers missing and the remaining two at 87% efficiency, the capacity is 58% (2⁄3 of 87%).[16][17]
Where a delta-fed system must be grounded for detection of stray current to ground or protection from surge voltages, a grounding transformer (usually a zigzag transformer) may be connected to allow ground fault currents to return from any phase to ground. Another variation is a "corner grounded" delta system, which is a closed delta that is grounded at one of the junctions of transformers.[18]
Three-wire and four-wire circuits[edit]

There are two basic three-phase configurations: wye (Y) and delta (Δ). As shown in the diagram, a delta configuration requires only three wires for transmission, but a wye (star) configuration may have a fourth wire. The fourth wire, if present, is provided as a neutral and is normally grounded. The three-wire and four-wire designations do not count the ground wire present above many transmission lines, which is solely for fault protection and does not carry current under normal use.
A four-wire system with symmetrical voltages between phase and neutral is obtained when the neutral is connected to the "common star point" of all supply windings. In such a system, all three phases will have the same magnitude of voltage relative to the neutral. Other non-symmetrical systems have been used.
The four-wire wye system is used when a mixture of single-phase and three-phase loads are to be served, such as mixed lighting and motor loads. An example of application is local distribution in Europe (and elsewhere), where each customer may be only fed from one phase and the neutral (which is common to the three phases). When a group of customers sharing the neutral draw unequal phase currents, the common neutral wire carries the currents resulting from these imbalances. Electrical engineers try to design the three-phase power system for any one location so that the power drawn from each of three phases is the same, as far as possible at that site.[19] Electrical engineers also try to arrange the distribution network so the loads are balanced as much as possible, since the same principles that apply to individual premises also apply to the wide-scale distribution system power. Hence, every effort is made by supply authorities to distribute the power drawn on each of the three phases over a large number of premises so that, on average, as nearly as possible a balanced load is seen at the point of supply.

For domestic use, some countries such as the UK may supply one phase and neutral at a high current (up to 100 A) to one property, while others such as Germany may supply 3 phases and neutral to each customer, but at a lower fuse rating, typically 40–63 A per phase, and "rotated" to avoid the effect that more load tends to be put on the first phase.[citation needed]

Based on wye (Y) and delta (Δ) connection. Generally, there are four different types of three-phase transformer winding connections for transmission and distribution purposes:
- wye (Y) – wye (Y) is used for small current and high voltage,
- Delta (Δ) – Delta (Δ) is used for large currents and low voltages,
- Delta (Δ) – wye (Y) is used for step-up transformers, i.e., at generating stations,
- wye (Y) – Delta (Δ) is used for step-down transformers, i.e., at the end of the transmission.
In North America, a high-leg delta supply is sometimes used where one winding of a delta-connected transformer feeding the load is center-tapped and that center tap is grounded and connected as a neutral as shown in the second diagram. This setup produces three different voltages: If the voltage between the center tap (neutral) and each of the top and bottom taps (phase and anti-phase) is 120 V (100%), the voltage across the phase and anti-phase lines is 240 V (200%), and the neutral to "high leg" voltage is ≈ 208 V (173%).[15]
The reason for providing the delta connected supply is usually to power large motors requiring a rotating field. However, the premises concerned will also require the "normal" North American 120 V supplies, two of which are derived (180 degrees "out of phase") between the "neutral" and either of the center-tapped phase points.
Balanced circuits[edit]
In the perfectly balanced case all three lines share equivalent loads. Examining the circuits, we can derive relationships between line voltage and current, and load voltage and current for wye- and delta-connected loads.
In a balanced system each line will produce equal voltage magnitudes at phase angles equally spaced from each other. With V1 as our reference and V3 lagging V2 lagging V1, using angle notation, and VLN the voltage between the line and the neutral we have:[20]
These voltages feed into either a wye- or delta-connected load.
Wye (or, star; Y)[edit]

The voltage seen by the load will depend on the load connection; for the wye case, connecting each load to a phase (line-to-neutral) voltages gives[20]
where Ztotal is the sum of line and load impedances (Ztotal = ZLN + ZY), and θ is the phase of the total impedance (Ztotal).
The phase angle difference between voltage and current of each phase is not necessarily 0 and depends on the type of load impedance, Zy. Inductive and capacitive loads will cause current to either lag or lead the voltage. However, the relative phase angle between each pair of lines (1 to 2, 2 to 3, and 3 to 1) will still be −120°.

- Vab = (1∠α − 1∠α + 120°) √3 |V|∠α + 30°,
- Vbc = √3 |V|∠α − 90°,
- Vca = √3 |V|∠α + 150°
By applying Kirchhoff's current law (KCL) to the neutral node, the three phase currents sum to the total current in the neutral line. In the balanced case:
Delta (Δ)[edit]
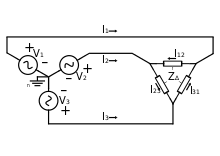
In the delta circuit, loads are connected across the lines, and so loads see line-to-line voltages:[20]
(Φv1 is the phase shift for the first voltage, commonly taken to be 0°; in this case, Φv2 = −120° and Φv3 = −240° or 120°.)
Further:
where θ is the phase of delta impedance (ZΔ).
Relative angles are preserved, so I31 lags I23 lags I12 by 120°. Calculating line currents by using KCL at each delta node gives
and similarly for each other line:
where, again, θ is the phase of delta impedance (ZΔ).

- Ia = Iab − Ica = √3 Iab∠−30°,
- Ib = Ibc − Iab,
- Ic = Ica − Ibc.
- S3Φ = 3VphaseI*phase.
Inspection of a phasor diagram, or conversion from phasor notation to complex notation, illuminates how the difference between two line-to-neutral voltages yields a line-to-line voltage that is greater by a factor of √3. As a delta configuration connects a load across phases of a transformer, it delivers the line-to-line voltage difference, which is √3 times greater than the line-to-neutral voltage delivered to a load in the wye configuration. As the power transferred is V2/Z, the impedance in the delta configuration must be 3 times what it would be in a wye configuration for the same power to be transferred.
Single-phase loads[edit]
Except in a high-leg delta system and a corner-grounded delta system, single-phase loads may be connected across any two phases, or a load can be connected from phase to neutral.[22] Distributing single-phase loads among the phases of a three-phase system balances the load and makes most economical use of conductors and transformers.
In a symmetrical three-phase four-wire wye system, the three phase conductors have the same voltage to the system neutral. The voltage between line conductors is √3 times the phase conductor to neutral voltage:[23]
The currents returning from the customers' premises to the supply transformer all share the neutral wire. If the loads are evenly distributed on all three phases, the sum of the returning currents in the neutral wire is approximately zero. Any unbalanced phase loading on the secondary side of the transformer will use the transformer capacity inefficiently.
If the supply neutral is broken, phase-to-neutral voltage is no longer maintained. Phases with higher relative loading will experience reduced voltage, and phases with lower relative loading will experience elevated voltage, up to the phase-to-phase voltage.
A high-leg delta provides phase-to-neutral relationship of VLL = 2 VLN , however, LN load is imposed on one phase.[15] A transformer manufacturer's page suggests that LN loading not exceed 5% of transformer capacity.[24]
Since √3 ≈ 1.73, defining VLN as 100% gives VLL ≈ 100% × 1.73 = 173%. If VLL was set as 100%, then VLN ≈ 57.7%.
Unbalanced loads[edit]
When the currents on the three live wires of a three-phase system are not equal or are not at an exact 120° phase angle, the power loss is greater than for a perfectly balanced system. The method of symmetrical components is used to analyze unbalanced systems.
Non-linear loads[edit]
With linear loads, the neutral only carries the current due to imbalance between the phases. Gas-discharge lamps and devices that utilize rectifier-capacitor front-end such as switch-mode power supplies, computers, office equipment and such produce third-order harmonics that are in-phase on all the supply phases. Consequently, such harmonic currents add in the neutral in a wye system (or in the grounded (zigzag) transformer in a delta system), which can cause the neutral current to exceed the phase current.[22][25]
Three-phase loads[edit]

An important class of three-phase load is the electric motor. A three-phase induction motor has a simple design, inherently high starting torque and high efficiency. Such motors are applied in industry for many applications. A three-phase motor is more compact and less costly than a single-phase motor of the same voltage class and rating, and single-phase AC motors above 10 hp (7.5 kW) are uncommon. Three-phase motors also vibrate less and hence last longer than single-phase motors of the same power used under the same conditions.[26]
Resistive heating loads such as electric boilers or space heating may be connected to three-phase systems. Electric lighting may also be similarly connected.
Line frequency flicker in light is detrimental to high-speed cameras used in sports event broadcasting for slow-motion replays. It can be reduced by evenly spreading line frequency operated light sources across the three phases so that the illuminated area is lit from all three phases. This technique was applied successfully at the 2008 Beijing Olympics.[27]
Rectifiers may use a three-phase source to produce a six-pulse DC output.[28] The output of such rectifiers is much smoother than rectified single phase and, unlike single-phase, does not drop to zero between pulses. Such rectifiers may be used for battery charging, electrolysis processes such as aluminium production and the electric arc furnace used in steelmaking, and for operation of DC motors. Zigzag transformers may make the equivalent of six-phase full-wave rectification, twelve pulses per cycle, and this method is occasionally employed to reduce the cost of the filtering components, while improving the quality of the resulting DC.

In many European countries electric stoves are usually designed for a three-phase feed with permanent connection. Individual heating units are often connected between phase and neutral to allow for connection to a single-phase circuit if three-phase is not available.[29] Other usual three-phase loads in the domestic field are tankless water heating systems and storage heaters. Homes in Europe have standardized on a nominal 230 V ±10% between any phase and ground. Most groups of houses are fed from a three-phase street transformer so that individual premises with above-average demand can be fed with a second or third phase connection.
Phase converters[edit]
Phase converters are used when three-phase equipment needs to be operated on a single-phase power source. They are used when three-phase power is not available or cost is not justifiable. Such converters may also allow the frequency to be varied, allowing speed control. Some railway locomotives use a single-phase source to drive three-phase motors fed through an electronic drive.[30]
A rotary phase converter is a three-phase motor with special starting arrangements and power factor correction that produces balanced three-phase voltages. When properly designed, these rotary converters can allow satisfactory operation of a three-phase motor on a single-phase source. In such a device, the energy storage is performed by the inertia (flywheel effect) of the rotating components. An external flywheel is sometimes found on one or both ends of the shaft.
A three-phase generator can be driven by a single-phase motor. This motor-generator combination can provide a frequency changer function as well as phase conversion, but requires two machines with all their expenses and losses. The motor-generator method can also form an uninterruptible power supply when used in conjunction with a large flywheel and a battery-powered DC motor; such a combination will deliver nearly constant power compared to the temporary frequency drop experienced with a standby generator set gives until the standby generator kicks in.
Capacitors and autotransformers can be used to approximate a three-phase system in a static phase converter, but the voltage and phase angle of the additional phase may only be useful for certain loads.
Variable-frequency drives and digital phase converters use power electronic devices to synthesize a balanced three-phase supply from single-phase input power.
Testing[edit]
Verification of the phase sequence in a circuit is of considerable practical importance. Two sources of three-phase power must not be connected in parallel unless they have the same phase sequence, for example, when connecting a generator to an energized distribution network or when connecting two transformers in parallel. Otherwise, the interconnection will behave like a short circuit, and excess current will flow. The direction of rotation of three-phase motors can be reversed by interchanging any two phases; it may be impractical or harmful to test a machine by momentarily energizing the motor to observe its rotation. Phase sequence of two sources can be verified by measuring voltage between pairs of terminals and observing that terminals with very low voltage between them will have the same phase, whereas pairs that show a higher voltage are on different phases.
Where the absolute phase identity is not required, phase rotation test instruments can be used to identify the rotation sequence with one observation. The phase rotation test instrument may contain a miniature three-phase motor, whose direction of rotation can be directly observed through the instrument case. Another pattern uses a pair of lamps and an internal phase-shifting network to display the phase rotation. Another type of instrument can be connected to a de-energized three-phase motor and can detect the small voltages induced by residual magnetism, when the motor shaft is rotated by hand. A lamp or other indicator lights to show the sequence of voltages at the terminals for the given direction of shaft rotation.[31]
Alternatives to three-phase[edit]
- Split-phase electric power
- Used when three-phase power is not available and allows double the normal utilization voltage to be supplied for high-power loads.
- Two-phase electric power
- Uses two AC voltages, with a 90-electrical-degree phase shift between them. Two-phase circuits may be wired with two pairs of conductors, or two wires may be combined, requiring only three wires for the circuit. Currents in the common conductor add to 1.4 times ( ) the current in the individual phases, so the common conductor must be larger. Two-phase and three-phase systems can be interconnected by a Scott-T transformer, invented by Charles F. Scott.[32] Very early AC machines, notably the first generators at Niagara Falls, used a two-phase system, and some remnant two-phase distribution systems still exist, but three-phase systems have displaced the two-phase system for modern installations.
- Monocyclic power
- An asymmetrical modified two-phase power system used by General Electric around 1897, championed by Charles Proteus Steinmetz and Elihu Thomson. This system was devised to avoid patent infringement. In this system, a generator was wound with a full-voltage single-phase winding intended for lighting loads and with a small fraction (usually 1/4 of the line voltage) winding that produced a voltage in quadrature with the main windings. The intention was to use this "power wire" additional winding to provide starting torque for induction motors, with the main winding providing power for lighting loads. After the expiration of the Westinghouse patents on symmetrical two-phase and three-phase power distribution systems, the monocyclic system fell out of use; it was difficult to analyze and did not last long enough for satisfactory energy metering to be developed.
- High-phase-order systems
- Have been built and tested for power transmission. Such transmission lines typically would use six or twelve phases. High-phase-order transmission lines allow transfer of slightly less than proportionately higher power through a given volume without the expense of a high-voltage direct current (HVDC) converter at each end of the line. However, they require correspondingly more pieces of equipment.
- DC
- AC was historically used because it could be easily transformed to higher voltages for long distance transmission. However modern electronics can raise the voltage of DC with high efficiency, and DC lacks skin effect which permits transmission wires to be lighter and cheaper and so high-voltage direct current gives lower losses over long distances.
Color codes[edit]
Conductors of a three-phase system are usually identified by a color code, to facilitate balanced loading and to assure the correct phase rotation for motors. Colors used may adhere to International Standard IEC 60446 (later IEC 60445), older standards or to no standard at all and may vary even within a single installation. For example, in the U.S. and Canada, different color codes are used for grounded (earthed) and ungrounded systems.
| Country | Phases[note 1] | Neutral, N[note 2] |
Protective earth, PE[note 3] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | ||||||||||
| Australia and New Zealand (AS/NZS 3000:2007 Figure 3.2, or IEC 60446 as approved by AS:3000) | Red, or brown[note 4] | White;[note 4] prev. yellow | Dark blue, or grey[note 4] | Black, or blue[note 4] | Green/yellow-striped (installations prior to 1966: green) | |||||||
| Canada | Mandatory[33] | Red[note 5] | Black | Blue | White, or grey | Green, perhaps yellow-striped, or uninsulated | ||||||
| Isolated systems[34] | Orange | Brown | Yellow | White, or grey | Green perhaps yellow-striped | |||||||
| European CENELEC (European Union and others; since April 2004, IEC 60446, later IEC 60445-2017), United Kingdom (since 31 March 2004), Hong Kong (from July 2007), Singapore (from March 2009), Russia (since 2009; GOST R 50462), Argentina, Ukraine, Belarus, Kazakhstan, South Korea (from Jan. 2021) | Brown | Black | Grey | Blue | Green/yellow-striped[note 6] | |||||||
| Older European (prior to IEC 60446, varied by country)[note 7] | ||||||||||||
| UK (before April 2006), Hong Kong (before April 2009), South Africa, Malaysia, Singapore (before February 2011) | Red | Yellow | Blue | Black | Green/yellow-striped (before c. 1970: green) | |||||||
| India | Red | Yellow | Blue | Black | Green, perhaps yellow-striped | |||||||
| Chile – NCH 4/2003 | Blue | Black | Red | White | Green, perhaps yellow-striped | |||||||
| Former USSR (Russia, Ukraine, Kazakhstan; before 2009), People's Republic of China[note 8] (GB 50303-2002 Section 15.2.2) | Yellow | Green | Red | Sky blue | Green/yellow-striped | |||||||
| Norway (before CENELEC adoption) | Black | White/grey | Brown | Blue | Yellow/green-striped; prev. yellow or uninsulated | |||||||
| United States[note 9] | 120, 208, or 240 V | Black | Red | Blue | White | Bare Conductor (no insulation) | ||||||
| 277 or 480 V | Brown | Orange | Yellow | Gray | Bare Conductor (no insulation) | |||||||
| Alternate Practices (Delta with tapped winding) | Black | Orange
(High-Leg[note 10]) |
Red | White | Green or Yellow/green-striped or no insulation | |||||||
| Blue | ||||||||||||
See also[edit]
Notes[edit]
- ^ Many labelling systems exist for phases, some having additional meaning, such as: H1, H2, H3; A, B, C; R, S, T; U, V, W; R, Y, B.
- ^ Also, grounded conductor.
- ^ Also, earth, or grounding conductor.
- ^ a b c d In Australia and New Zealand, active conductors can be any color except green/yellow, green, yellow, black, or light blue. Yellow is no longer permitted in the 2007 revision of wiring code ASNZS 3000. European color codes are used for all IEC or flex cables such as extension leads, appliance leads etc. and are equally permitted for use in building wiring per AS/NZS 3000:2007.
- ^ In Canada the high leg conductor in a high-leg delta system is always marked red.
- ^ The international standard green-yellow marking of protective-earth conductors was introduced to reduce the risk of confusion by color blind installers. About 7% to 10% of men cannot clearly distinguish between red and green, which is a particular concern in older schemes where red marks a live conductor and green marks protective earth or safety ground.
- ^ In Europe, there still exist many installations with older colors but, since the early 1970s, all new installations use green/yellow earth according to IEC 60446. (E.g. phase/neutral & earth, German: black/grey & red; France: green/red & white; Russia: red/grey & black; Switzerland: red/grey & yellow or yellow & red; Denmark: white/black & red.
- ^ Note that while China officially uses phase 1: yellow, phase 2: green, phase 3: red, neutral: blue, ground: green/yellow, this is not strongly enforced and there is significant local variation.
- ^ Since 1975, the U.S. National Electric Code has not specified coloring of phase conductors. It is common practice in many regions to identify 120/208 V (wye) conductors as black, red, and blue, and 277/480 V (wye or delta) conductors as brown, orange, yellow. In a 120/240 V delta system with a 208 V high leg, the high leg (typically B phase) is always marked orange, commonly A phase is black and C phase is either red or blue. Local regulations may amend the N.E.C. The U.S. National Electric Code has color requirements for grounded conductors, ground, and grounded-delta three-phase systems which result in one ungrounded leg having a higher voltage potential to ground than the other two ungrounded legs.
- ^ Must be the high leg, if it is present.
References[edit]
- ^ Saleh, S. A.; Rahman, M. A. (25 March 2013). "The analysis and development of controlled 3φ wavelet modulated AC-DC converter". 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES). pp. 1–6. doi:10.1109/PEDES.2012.6484282. ISBN 978-1-4673-4508-8. S2CID 32935308.
- ^ William D. Stevenson, Jr. Elements of Power System Analysis Third Edition, McGraw-Hill, New York (1975). ISBN 0-07-061285-4, p. 2
- ^ Terrell Croft, Wilford Summers (ed), American Electricians' Handbook, 11th ed., McGraw Hill, 1987 ISBN 0-07-013932-6 page 3-10 figure 3-23.
- ^ Brumbach, Michael (2014). Industrial maintenance. Clifton Park, NY: Delmar, Cengage Learning. p. 411. ISBN 9781133131199.
- ^ "AC Power History and Timeline". Edison Tech Center. Retrieved January 24, 2022.
- ^ Woodbank Communications Ltd.'s Electropaedia: "History of Batteries (and other things)"
- ^ Gerhard Neidhöfer: Michael von Dolivo-Dobrowolsky und der Drehstrom. Geschichte der Elektrotechnik VDE-Buchreihe, Volume 9, VDE VERLAG, Berlin Offenbach, ISBN 978-3-8007-3115-2.
- ^ Bergström och Nordlund, Lars (2002). Ellära- Kretsteknik och fältteori. Naturaläromedel. p. 283. ISBN 91-7536-330-5.
- ^ Hjulström, Filip (1940). Elektrifieringens utveckling i Sverige, en ekonomisk-geografisk översikt. [Excerpt taken from YMER 1941, häfte 2.Utgiven av Sällskapet för antropologi och geografi: Meddelande från Upsala univeristets geografiska institution, N:o 29, published by Esselte ab, Stockholm 1941 no. 135205]
- ^ von Meier, Alexandra (2006). Electric Power Systems. Hoboken, New Jersey: John Wiley & Sons, Inc. p. 160. ISBN 978-0-471-17859-0.
We also stated one rationale for this three-phase system; namely, that a three-phase generator experiences a constant torque on its rotor as opposed to the pulsating torque that appears in a single- or two-phase machine, which is obviously preferable from a mechanical engineering standpoint.
- ^ Cotton, H, Electrical Technology, 6th ed., Pitman, London, 1950, p. 268.
- ^ Hawkins Electrical Guide, Theo. Audel and Co., 2nd ed., 1917, vol. 4, Ch. 46: Alternating Currents, p. 1026, fig. 1260.
- ^ Hawkins Electrical Guide, Theo. Audel and Co., 2nd ed., 1917, vol. 4, Ch. 46: Alternating Currents, p. 1026, fig. 1261.
- ^ "A New Design for Automotive Alternators" (PDF). August 30, 2017. Archived from the original (PDF) on 2017-08-30.
- ^ a b c Fowler, Nick (2011). Electrician's Calculations Manual 2nd Edition. McGraw-Hill. pp. 3–5. ISBN 978-0-07-177017-0.
- ^ Gibbs, J. B. (April 27, 1920). "Three-Phase Power from Single-Phase Transformer Connections". Power. 51 (17). McGraw-Hill: 673. Retrieved 21 December 2012.
- ^ H. W. Beaty, D. G. Fink (ed.), Standard Handbook for Electrical Engineers Fifteenth Edition, McGraw-Hill, 2007, ISBN 0-07-144146-8, p. 10–11.
- ^ "Schneider" (PDF). Archived (PDF) from the original on 2022-10-09.
- ^ "Saving energy through load balancing and load scheduling" (PDF). Archived from the original (PDF) on 2014-09-11. Retrieved 2014-08-03.
- ^ a b c J. Duncan Glover; Mulukutla S. Sarma; Thomas J. Overbye (April 2011). Power System Analysis & Design. Cengage Learning. pp. 60–68. ISBN 978-1-111-42579-1.
- ^ "What is "Stray Voltage"?" (PDF). Utility Technology Engineers-Consultants (UTEC). August 10, 2015. Retrieved December 10, 2023.
- ^ a b Lowenstein, Michael. "The 3rd Harmonic Blocking Filter: A Well Established Approach to Harmonic Current Mitigation". IAEI Magazine. Archived from the original on 8 September 2013. Retrieved 24 November 2012.
- ^ The boy electrician by J. W. Sims M.I.E.E. (Page 98).
- ^ "Federal pacific". Archived from the original on May 30, 2012.
- ^ Enjeti, Prasad. "Harmonics in Low Voltage Three-Phase Four-Wire Electric Distribution Systems and Filtering Solutions" (PDF). Texas A&M University Power Electronics and Power Quality Laboratory. Archived from the original (PDF) on 13 June 2010. Retrieved 24 November 2012.
- ^ Alexander, Charles K.; Sadiku, Matthew N. O. (2007). Fundamentals of Electric Circuits. New York, NY: McGraw-Hill. p. 504. ISBN 978-0-07-297718-9.
- ^ Hui, Sun. "Sports Lighting – Design Considerations For The Beijing 2008 Olympic Games" (PDF). GE Lighting. Archived from the original (PDF) on 28 April 2015. Retrieved 18 December 2012.
- ^ Pekarek, Steven; Skvarenina, Timothy (November 1998). "ACSL/Graphic Modeller Component Models for Electric Power Education". IEEE Transactions on Education. 41 (4): 348. Bibcode:1998ITEdu..41..348P. doi:10.1109/TE.1998.787374.
- ^ "British and European practices for domestic appliances compared", Electrical Times, volume 148, page 691, 1965.
- ^ "Speeding-up Conventional Lines and Shinkansen" (PDF). Japan Railway & Transport Review. 58: 58. Oct 2011. Archived (PDF) from the original on 2022-10-09.
- ^ Steve Sentry, "Motor Control Fundamentals", Cengage Learning, 2012, ISBN 1133709176, page 70
- ^ Brittain, J. E. (2007). "Electrical Engineering Hall of Fame: Charles F. Scott". Proceedings of the IEEE. 95 (4): 836–839. doi:10.1109/JPROC.2006.892488.
- ^ C22.1-15—Canadian Electrical Code, Part I: Safety Standard for Electrical Installations (23rd ed.). Canadian Standards Association. 2015. Rule 4–038. ISBN 978-1-77139-718-6.
- ^ C22.1-15—Canadian Electrical Code, Part I: Safety Standard for Electrical Installations (23rd ed.). Canadian Standards Association. 2015. Rule 24–208(c). ISBN 978-1-77139-718-6.














