Jump to content

Wythoff symbol

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Tomruen (talk | contribs) at 15:58, 28 January 2007 (→‎References). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Example Wythoff construction triangles with the 7 generator points. Lines to the active mirrors are colored red, yellow, and blue with the 3 nodes opposite them as associated by the Wythoff symbol.

In geometry, a Wythoff symbol is a short-hand notation, created by mathematician Willem Abraham Wythoff, for naming the regular and semiregular polyhedra using a kaleidoscopic construction, by representing them as tilings on the surface of a sphere, Euclidean plane, or hyperbolic plane.

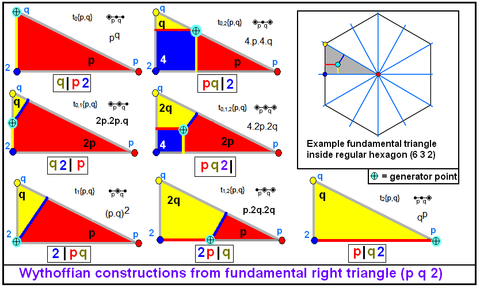
The Wythoff symbol gives 3 numbers p,q,r and a positional vertical bar (|) which separate the numbers before or after it. Each number represents the order of mirrors at a vertex of the fundamental triangle.

Each symbol represents one uniform polyhedron or tiling, although the same tiling/polyhedron can have different Wythoff symbols from different symmetry generators. For example, the regular cube can be represented by 3 | 4 2 with Oh symmetry, and 2 4 | 2 as a square prism with 2 colors and D4h symmetry, as well as 2 2 2 | with 3 colors and D2h symmetry.

Summary table

The 8 forms for the Wythoff constructions from a general triangle (p q r).

There are 7 generator points with each set of p,q,r: (And a few special forms)

General Right triangle (r=2)
Description Wythoff
symbol 		Vertex
configuration 		Wythoff
symbol 		Vertex
configuration
regular and
quasiregular 		q | p r (p.r)q q | p 2 pq
p | q r (q.r)p p | q 2 qp
r | p q (q.p)r 2 | p q (q.p)2
truncated and
expanded 		q r | p q.2p.r.2p q 2 | p q.2p.2p
p r | q p.2q.r.2q p 2 | q p.2q.2q
p q | r 2r.q.2r.p p q | 2 4.q.4.p
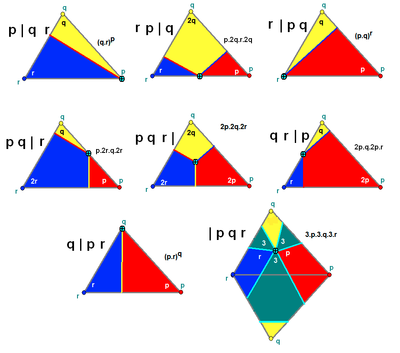
even-faced p q r | 2r.2q.2p p q 2 | 4.2q.2p
p q (r s) | 2p.2q.-2p.-2q p 2 (r s) | 2p.4.-2p.4/3
snub | p q r 3.r.3.q.3.p | p q 2 3.3.q.3.p
| p q r s (4.p.4.q.4.r.4.s)/2 - -

There are three special cases:

  • p q (r s) | - This is a mixture of p q r | and p q s |.
  • | p q r - Snub forms (alternated) are give this otherwise unused symbol.
  • | p q r s - A unique snub form for U75 that isn't Wythoff constructable.

Description

The p,q,r represent the shape of the fundamental triangle fo the symmetry, specifically each number is the number of reflectional mirrors that exist at each vertex. On the sphere there are 3 main symmetry types: (3 3 2), (4 3 2), (5 3 2), and one infinite family (p 2 2), for any p=2,3,... (All simple families have one right angle and so r=2)

The position of the vertical bar in the symbol is used to imply a specific forms (a categorical position of the generator point) within the fundamental triangle. The generator point can either be on or off each mirror, activated or not. This distinction creates 8 (23) possible forms, neglecting one where the generator point is on all the mirrors.

In this notation the mirrors are labeled by the reflection-order of the opposite vertex. The p,q,r values are listed before the bar if the corresponding mirror is active.

The one impossible symbol | p q r, which implies the the generator point is on all mirrors which is only possible if the triangle is generated to a point. This unused symbol is reassigned to mean something different. This symbols represents the case where all mirrors are active, but odd-numbered reflected images are ignored. This creates a rotational symmetry results.

This symbol is functionally similar to the more general Coxeter-Dynkin diagram which shows a triangle marked as p, q, r on the edges, and circles the nodes, representing the mirrors to imply whether the generator point was touching that mirror. (The Coxeter-Dynkin diagram is show as a linear graph when r=2 since there's no interacting reflections across a right angle.)

Symmetry triangles

There are 4 symmetry classes of reflection on the sphere, and two for the Euclidean plane, and infinitely many for the hyperbolic plane, the first:

  1. (p 2 2) dihedral symmetry p=2,3,4... (Order 4p)
  2. (3 3 2) tetrahedral symmetry (Order 24)
  3. (4 3 2) octahedral symmetry (Order 48)
  4. (5 3 2) icosahedral symmetry (Order 120)
  5. (4 4 2) - *442 symmetry - 45-45-90 triangle (Includes square domain (2 2 2 2))
  6. (3 3 3) - *333 symmetry - 60-60-60 triangle
  7. (6 3 2) - *632 symmetry - 30-60-90 triangle
  8. (7 3 2) - *732 symmetry (Hyperbolic plane)
Dihedral spherical Spherical
D2h D3h Td Oh Ih
*222 *322 *332 *432 *532

(2 2 2)
(3 2 2)
( 3 3 2)
(4 3 2)
(5 3 2)

The above symmetry groups only includes the integer solutions on the sphere. The list of Schwarz triangles includes rational numbers, and determine the full set of solutions of uniform polyhedrons.

Euclidean plane Hyperbolic
p4m p3m p6m  
*442 *333 *632 *732

(4 4 2)
(3 3 3)
(6 3 2)
(7 3 2)

In the tilings above, each triangle is a fundamental domain, colored by even and odd reflections.

Summary spherical and plane tilings

An selection of tilings created by the Wythoff construction are given below.

Spherical tilings (r=2)

(p q 2) Fund.
triangle 		Parent Truncated Rectified Bitruncated Birectified
(dual) 		Cantellated Omnitruncated
(Cantitruncated) 		Snub
Wythoff symbol q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Schläfli symbol t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Coxeter-Dynkin diagram
Vertex figure pq (q.2p.2p) (p.q.p.q) (p.2q.2q) qp (p.4.q.4) (4.2p.2q) (3.3.p.3.q)
Tetrahedral
(3 3 2)
{3,3} 		File:Uniform tiling 332-t01.png
(3.6.6) 		File:Uniform tiling 332-t1.png
(3.3a.3.3a)
(3.6.6)
{3,3}
(3a.4.3b.4)
(4.6a.6b)
(3.3.3a.3.3b)
Octahedral
(4 3 2)
{4,3}
(3.8.8)
(3.4.3.4)
(4.6.6)
{3,4}
(3.4.4a.4)
(4.6.8)
(3.3.3a.3.4)
Icosahedral
(5 3 2)
{5,3}
(3.10.10)
(3.5.3.5)
(5.6.6)
{3,5}
(3.4.5.4)
(4.6.10)
(3.3.3a.3.5)

Planar tilings (r=2)

One representative hyperbolic tiling is given, and shown as a Poincaré disk projection.

(p q 2) Fund.
triangle 		Parent Truncated Rectified Bitruncated Birectified
(dual) 		Cantellated Omnitruncated
(Cantitruncated) 		Snub
Wythoff symbol q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Schläfli symbol t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Coxeter-Dynkin diagram
Square tiling
(4 4 2)
{4,4}
4.8.8
4.4a.4.4a
4.8.8
{4,4}
4.4a.4b.4a
4.8.8
3.3.4a.3.4b
Hexagonal tiling
(6 3 2)
{6,3}
3.12.12
3.6.3.6
6.6.6
{3,6}
3.4.6.4
4.6.12
3.3.3.3.6
(Hyperbolic plane)
(7 3 2)
{7,3}
3.14.14
3.7.3.7
7.6.6
{3,7}
3.4.7.4
4.6.14
3.3.3.3.7

Planar tilings (r>2)

The Coxeter-Dynkin diagram is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.

Wythoff symbol
(p q r) 		Fund.
triangle 		q | p r r q | p r | p q r p | q p | q r p q | r p q r | | p q r
Coxeter-Dynkin diagram
Triangular
(3 3 3)
(3.3)3
3a.6.3b.6
(3.3)3
3a.6.3b.6
(3.3)3
3a.6.3b.6
6a.6b.6c
3.3a.3.3b.3.3c

Overlapping spherical tilings (r=2)

Tilings are shown as polyhedra. Some of the forms are degenerate, given with brackets for vertex figures, with overlapping edges or verices.

(p q 2) Fund.
triangle 		Parent Truncated Rectified Bitruncated Birectified
(dual) 		Cantellated Omnitruncated
(Cantitruncated) 		Snub
Wythoff symbol q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Schläfli symbol t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Coxeter-Dynkin diagram
Icosahedral
5/2-3-2 		 
{3,5/2}
(5/2.6.6)
(3.5/2)2
[3.10/2.10/2]
{5/2,3}
[3.4.5/2.4]
[4.10/2.6]
(3.3.3.3.5/2)
Icosahedral
5-5/2-2 		 
{5,5/2}
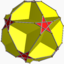(5/2.10.10)
(5/2.5)2
[5.10/2.10/2]
{5/2,5}
(5/2.4.5.4)
[4.10/2.10]
(3.3.5/2.3.5)

See also

References

  • Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
  • Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
  • Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50.
  • Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. pp. 9-10.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Wythoff_symbol&oldid=103854359"