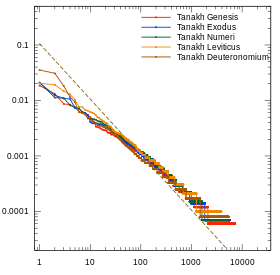Zipf's law


Zipf's law (/zɪf/, German: [t͡sɪpf]) is an empirical law that often holds, approximately, when a list of measured values is sorted in decreasing order. It states that the value of the nth entry is inversely proportional to n.
The best known instance of Zipf's law applies to the frequency table of words in a text or corpus of natural language: It is usually found that the most common word occurs approximately twice as often as the next common one, three times as often as the third most common, and so on. For example, in the Brown Corpus of American English text, the word "the" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place word "of" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "and" (28,852).[2] It is often used in the following form, called Zipf-Mandelbrot law:where are fitted parameters, with , and .[1]
This law is named after the American linguist George Kingsley Zipf,[3][4][5] and is still an important concept in quantitative linguistics. It has been found to apply to many other types of data studied in the physical and social sciences.
In mathematical statistics, the concept has been formalized as the Zipfian distribution: a family of related discrete probability distributions whose rank-frequency distribution is an inverse power law relation. They are related to Benford's law and the Pareto distribution.
Some sets of time-dependent empirical data deviate somewhat from Zipf's law. Such empirical distributions are said to be quasi-Zipfian.
History
[edit]In 1913, the German physicist Felix Auerbach observed an inverse proportionality between the population sizes of cities, and their ranks when sorted by decreasing order of that variable.[6]
Zipf's law has been discovered before Zipf,[a] by the French stenographer Jean-Baptiste Estoup' Gammes Stenographiques (4th ed) in 1916,[7] with G. Dewey in 1923,[8] and with E. Condon in 1928.[9]
The same relation for frequencies of words in natural language texts was observed by George Zipf in 1932,[4] but he never claimed to have originated it. In fact, Zipf did not like mathematics. In his 1932 publication,[10] the author speaks with disdain about mathematical involvement in linguistics, a. o. ibidem, p. 21: (…) let me say here for the sake of any mathematician who may plan to formulate the ensuing data more exactly, the ability of the highly intense positive to become the highly intense negative, in my opinion, introduces the devil into the formula in the form of . The only mathematical expression Zipf used looks like a.b2 = constant, which he "borrowed" from Alfred J. Lotka's 1926 publication.[11]
The same relationship was found to occur in many other contexts, and for other variables besides frequency.[1] For example, when corporations are ranked by decreasing size, their sizes are found to be inversely proportional to the rank.[12] The same relation is found for personal incomes (where it is called Pareto principle[13]), number of people watching the same TV channel,[14] notes in music,[15] cells transcriptomes,[16][17] and more.
In 1992 bioinformatician Wentian Li published a short paper[18] showing that Zipf's law emerges even in randomly generated texts. It included proof that the power law form of Zipf's law was a byproduct of ordering words by rank.
Formal definition
[edit]|
Probability mass function  Zipf PMF for N = 10 on a log–log scale. The horizontal axis is the index k. (The function is only defined at integer values of k. The connecting lines do not indicate continuity.) | |||
|
Cumulative distribution function 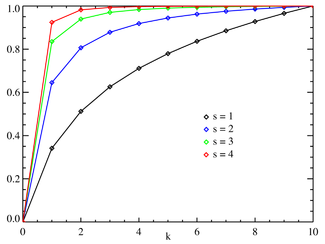 Zipf CDF for N = 10. The horizontal axis is the index k . (The function is only defined at integer values of k. The connecting lines do not indicate continuity.) | |||
| Parameters |
(real) (integer) | ||
|---|---|---|---|
| Support | |||
| PMF | where HN,s is the Nth generalized harmonic number | ||
| CDF | |||
| Mean | |||
| Mode | |||
| Variance | |||
| Entropy | |||
| MGF | |||
| CF | |||
Formally, the Zipf distribution on N elements assigns to the element of rank k (counting from 1) the probability
where HN is a normalization constant, the Nth harmonic number:
The distribution is sometimes generalized to an inverse power law with exponent s instead of 1.[19] Namely,
where HN,s is a generalized harmonic number
The generalized Zipf distribution can be extended to infinitely many items (N = ∞) only if the exponent s exceeds 1. In that case, the normalization constant HN,s becomes Riemann's zeta function,
If the exponent s is 1 or less, the normalization constant HN,s diverges as N tends to infinity.
Empirical testing
[edit]Empirically, a data set can be tested to see whether Zipf's law applies by checking the goodness of fit of an empirical distribution to the hypothesized power law distribution with a Kolmogorov–Smirnov test, and then comparing the (log) likelihood ratio of the power law distribution to alternative distributions like an exponential distribution or lognormal distribution.[20]
Zipf's law can be visuallized by plotting the item frequency data on a log-log graph, with the axes being the logarithm of rank order, and logarithm of frequency. The data conform to Zipf's law with exponent s to the extent that the plot approximates a linear (more precisely, affine) function with slope −s. For exponent s = 1, one can also plot the reciprocal of the frequency (mean interword interval) against rank, or the reciprocal of rank against frequency, and compare the result with the line through the origin with slope 1.[3]
Statistical explanations
[edit]Although Zipf's Law holds for most natural languages, and even some non-natural ones like Esperanto[21] and Toki Pona,[22] the reason is still not well understood.[23] Recent reviews of generative processes for Zipf's law include Mitzenmacher, "A Brief History of Generative Models for Power Law and Lognormal Distributions",[24] and Simkin, "Re-inventing Willis".[25]
However, it may be partly explained by statistical analysis of randomly generated texts. Wentian Li has shown that in a document in which each character has been chosen randomly from a uniform distribution of all letters (plus a space character), the "words" with different lengths follow the macro-trend of Zipf's law (the more probable words are the shortest and have equal probability).[26] In 1959, Vitold Belevitch observed that if any of a large class of well-behaved statistical distributions (not only the normal distribution) is expressed in terms of rank and expanded into a Taylor series, the first-order truncation of the series results in Zipf's law. Further, a second-order truncation of the Taylor series resulted in Mandelbrot's law.[27][28]
The principle of least effort is another possible explanation: Zipf himself proposed that neither speakers nor hearers using a given language wants to work any harder than necessary to reach understanding, and the process that results in approximately equal distribution of effort leads to the observed Zipf distribution.[5][29]
A minimal explanation assumes that words are generated by monkeys typing randomly. If language is generated by a single monkey typing randomly, with fixed and nonzero probability of hitting each letter key or white space, then the words (letter strings separated by white spaces) produced by the monkey follows Zipf's law.[30]
Another possible cause for the Zipf distribution is a preferential attachment process, in which the value x of an item tends to grow at a rate proportional to x (intuitively, "the rich get richer" or "success breeds success"). Such a growth process results in the Yule–Simon distribution, which has been shown to fit word frequency versus rank in language[31] and population versus city rank[32] better than Zipf's law. It was originally derived to explain population versus rank in species by Yule, and applied to cities by Simon.
A similar explanation is based on atlas models, systems of exchangeable positive-valued diffusion processes with drift and variance parameters that depend only on the rank of the process. It has been shown mathematically that Zipf's law holds for Atlas models that satisfy certain natural regularity conditions.[33][34]
Related laws
[edit]A generalization of Zipf's law is the Zipf–Mandelbrot law, proposed by Benoit Mandelbrot, whose frequencies are:
The constant C is the Hurwitz zeta function evaluated at s.
Zipfian distributions can be obtained from Pareto distributions by an exchange of variables.[19]
The Zipf distribution is sometimes called the discrete Pareto distribution[35] because it is analogous to the continuous Pareto distribution in the same way that the discrete uniform distribution is analogous to the continuous uniform distribution.
The tail frequencies of the Yule–Simon distribution are approximately
for any choice of ρ > 0.
In the parabolic fractal distribution, the logarithm of the frequency is a quadratic polynomial of the logarithm of the rank. This can markedly improve the fit over a simple power-law relationship.[36] Like fractal dimension, it is possible to calculate Zipf dimension, which is a useful parameter in the analysis of texts.[37]
It has been argued that Benford's law is a special bounded case of Zipf's law,[36] with the connection between these two laws being explained by their both originating from scale invariant functional relations from statistical physics and critical phenomena.[38] The ratios of probabilities in Benford's law are not constant. The leading digits of data satisfying Zipf's law with s = 1 satisfy Benford's law.
| Benford's law: |
||
|---|---|---|
| 1 | 0.30103000 | |
| 2 | 0.17609126 | −0.7735840 |
| 3 | 0.12493874 | −0.8463832 |
| 4 | 0.09691001 | −0.8830605 |
| 5 | 0.07918125 | −0.9054412 |
| 6 | 0.06694679 | −0.9205788 |
| 7 | 0.05799195 | −0.9315169 |
| 8 | 0.05115252 | −0.9397966 |
| 9 | 0.04575749 | −0.9462848 |
Occurrences
[edit]City sizes
[edit]Following Auerbach's 1913 observation, there has been substantial examination of Zipf's law for city sizes.[39] However, more recent empirical[40][41] and theoretical[42] studies have challenged the relevance of Zipf's law for cities.
Word frequencies in natural languages
[edit]
In many texts in human languages, word frequencies approximately follow a Zipf distribution with exponent s close to 1: that is, the most common word occurs about n times the nth most common one.
The actual rank-frequency plot of a natural language text deviates in some extent from the ideal Zipf distribution, especially at the two ends of the range. The deviations may depend on the language, on the topic of the text, on the author, on whether the text was translated from another language, and on the spelling rules used.[citation needed] Some deviation is inevitable because of sampling error.
At the low-frequency end, where the rank approaches N, the plot takes a staircase shape, because each word can occur only an integer number of times.
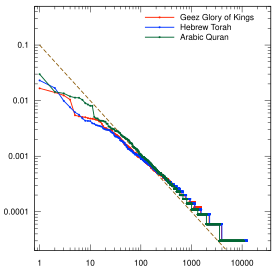
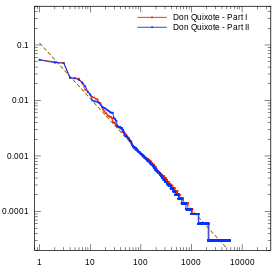
- Zipf's law plots for several languages
-
Biblical texts: Pentateuch from the Latin Vulgate and Russian Synodal Bible, the four Gospels from the Byzantine Greek Majority version
-
Cervantes's Don Quixote, Part I (1605) and Part II (1615)
-
First five books of the Old Testament (the Torah) in Hebrew, with vowels

In some Romance languages, the frequencies of the dozen or so most frequent words deviate significantly from the ideal Zipf distribution, because of those words include articles inflected for grammatical gender and number.[citation needed]
In many East Asian languages, such as Chinese, Lhasa Tibetan, and Vietnamese, each "word" consists of a single syllable; a word of English being often translated to a compound of two such syllables. The rank-frequency table for those "words" deviates significantly from the ideal Zipf law, at both ends of the range.[citation needed]
Even in English, the deviations from the ideal Zipf's law become more apparent as one examines large collections of texts. Analysis of a corpus of 30,000 English texts showed that only about 15% of the texts in it have a good fit to Zipf's law. Slight changes in the definition of Zipf's law can increase this percentage up to close to 50%.[43]
In these cases, the observed frequency-rank relation can be modeled more accurately as by separate Zipf–Mandelbrot laws distributions for different subsets or subtypes of words. This is the case for the frequency-rank plot of the first 10 million words of the English Wikipedia. In particular, the frequencies of the closed class of function words in English is better described with s lower than 1, while open-ended vocabulary growth with document size and corpus size require s greater than 1 for convergence of the Generalized Harmonic Series.[3]

When a text is encrypted in such a way that every occurrence of each distinct plaintext word is always mapped to the same encrypted word (as in the case of simple substitution ciphers, like the Caesar ciphers, or simple codebook ciphers), the frequency-rank distribution is not affected. On the other hand, if separate occurrences of the same word may be mapped to two or more different words (as happens with the Vigenère cipher), the Zipf distribution will typically have a flat part at the high-frequency end.[citation needed]
Applications
[edit]Zipf's law has been used for extraction of parallel fragments of texts out of comparable corpora.[44] Laurance Doyle and others have suggested the application of Zipf's law for detection of alien language in the search for extraterrestrial intelligence.[45][46]
The frequency-rank word distribution is often characteristic of the author and changes little over time. This feature has been used in the analysis of texts for authorship attribution.[47][48]
The word-like sign groups of the 15th-century codex Voynich Manuscript have been found to satisfy Zipf's law, suggesting that text is most likely not a hoax but rather written in an obscure language or cipher.[49][50]
See also
[edit]- 1% rule (Internet culture) – Hypothesis that more people will lurk in a virtual community than will participate
- Benford's law – Observation that in many real-life datasets, the leading digit is likely to be small
- Bradford's law – Pattern of references in science journals
- Brevity law – Linguistics law
- Demographic gravitation
- Frequency list – Bare list of a language's words in corpus linguistics
- Gibrat's law – Economic principle
- Hapax legomenon – Word that only appears once in a given text or record
- Heaps' law – Heuristic for distinct words in a document
- King effect – Phenomenon in statistics where highest-ranked data points are outliers
- Long tail – Feature of some statistical distributions
- Lorenz curve – Graphical representation of the distribution of income or of wealth
- Lotka's law – An application of Zipf's law describing the frequency of publication by authors in any given field
- Menzerath's law – Linguistic law
- Pareto distribution – Probability distribution
- Pareto principle – Statistical principle about ratio of effects to causes, a.k.a. the "80–20 rule"
- Price's law – Physicist and science historian (1922–1983)
- Principle of least effort – Idea that agents prefer to do what's easiest
- Rank-size distribution – distribution of size by rank
- Stigler's law of eponymy – Observation that no scientific discovery is named after its discoverer
- Letter frequency
- Most common words in English
Notes
[edit]References
[edit]- ^ a b c Piantadosi, Steven (March 25, 2014). "Zipf's word frequency law in natural language: A critical review and future directions". Psychon Bull Rev. 21 (5): 1112–1130. doi:10.3758/s13423-014-0585-6. PMC 4176592. PMID 24664880.
- ^ Fagan, Stephen; Gençay, Ramazan (2010), "An introduction to textual econometrics", in Ullah, Aman; Giles, David E. A. (eds.), Handbook of Empirical Economics and Finance, CRC Press, pp. 133–153, ISBN 9781420070361. P. 139: "For example, in the Brown Corpus, consisting of over one million words, half of the word volume consists of repeated uses of only 135 words."
- ^ a b c Powers, David M W (1998). Applications and explanations of Zipf's law. Joint conference on new methods in language processing and computational natural language learning. Association for Computational Linguistics. pp. 151–160. Archived from the original on 2015-09-10. Retrieved 2015-02-02.
- ^ a b George K. Zipf (1935): The Psychobiology of Language. Houghton-Mifflin.
- ^ a b c George K. Zipf (1949). Human Behavior and the Principle of Least Effort. Cambridge, Massachusetts: Addison-Wesley. p. 1.
- ^ Auerbach F. (1913) Das Gesetz der Bevölkerungskonzentration. Petermann’s Geographische Mitteilungen 59, 74–76
- ^ Christopher D. Manning, Hinrich Schütze Foundations of Statistical Natural Language Processing, MIT Press (1999), ISBN 978-0-262-13360-9, p. 24
- ^ Dewey, Godfrey. Relativ frequency of English speech sounds. Harvard University Press, 1923.
- ^ Condon, EDWARD U. "Statistics of vocabulary." Science 67.1733 (1928): 300-300.
- ^ George K. Zipf (1932): Selected Studies on the Principle of Relative Frequency in Language. Harvard, MA: Harvard University Press.
- ^ Zipf, George Kingsley (1942). "The Unity of Nature, Least-Action, and Natural Social Science". Sociometry. 5 (1): 48–62. doi:10.2307/2784953. ISSN 0038-0431. JSTOR 2784953. Archived from the original on 2022-11-20. Retrieved 2022-11-20.
- ^ Axtell, Robert L (2001): Zipf distribution of US firm sizes Archived 2023-10-17 at the Wayback Machine, Science, 293, 5536, 1818, American Association for the Advancement of Science.
- ^ Sandmo, Agnar (2015-01-01), Atkinson, Anthony B.; Bourguignon, François (eds.), Chapter 1 - The Principal Problem in Political Economy: Income Distribution in the History of Economic Thought, Handbook of Income Distribution, vol. 2, Elsevier, pp. 3–65, doi:10.1016/B978-0-444-59428-0.00002-3, ISBN 978-0-444-59430-3, archived from the original on 2023-10-29, retrieved 2023-07-11
- ^ M. Eriksson, S.M. Hasibur Rahman, F. Fraille, M. Sjöström, Efficient Interactive Multicast over DVB-T2 - Utilizing Dynamic SFNs and PARPS Archived 2014-05-02 at the Wayback Machine, 2013 IEEE International Conference on Computer and Information Technology (BMSB'13), London, UK, June 2013. Suggests a heterogeneous Zipf-law TV channel-selection model
- ^ Zanette, Damián H. (June 7, 2004). "Zipf's law and the creation of musical context". arXiv:cs/0406015.
- ^ Lazzardi, Silvia; Valle, Filippo; Mazzolini, Andrea; Scialdone, Antonio; Caselle, Michele; Osella, Matteo (2021-06-17). "Emergent Statistical Laws in Single-Cell Transcriptomic Data". bioRxiv: 2021–06.16.448706. doi:10.1101/2021.06.16.448706. S2CID 235482777. Archived from the original on 2021-06-17. Retrieved 2021-06-18.
- ^ Ramu Chenna, Toby Gibson; Evaluation of the Suitability of a Zipfian Gap Model for Pairwise Sequence Alignment Archived 2014-03-06 at the Wayback Machine, International Conference on Bioinformatics Computational Biology: 2011.
- ^ Li, Wentian (1992). "Random texts exhibit Zipf's-law-like word frequency distribution". IEEE Transactions on Information Theory. 38 (6): 1842–1845. doi:10.1109/18.165464 – via IEEE Xplore.
- ^ a b Adamic, Lada A. (2000). Zipf, power-laws, and Pareto - a ranking tutorial (Report). Hewlett-Packard Company. Archived from the original on 2023-04-01. Retrieved 2023-10-12. "originally published". www.parc.xerox.com. Xerox Corporation. Archived from the original on 2001-11-07. Retrieved 2016-02-23.
- ^ Clauset, A., Shalizi, C. R., & Newman, M. E. J. (2009). Power-Law Distributions in Empirical Data. SIAM Review, 51(4), 661–703. doi:10.1137/070710111
- ^ Bill Manaris; Luca Pellicoro; George Pothering; Harland Hodges (13 February 2006). Investigating Esperanto's statistical proportions relative to other languages using neural networks and Zipf's law (PDF). Artificial Intelligence and Applications. Innsbruck, Austria. pp. 102–108. Archived from the original (PDF) on 5 March 2016.
- ^ Skotarek, Dariusz (2020). Zipf's law in Toki Pona (PDF). ExLing Society. doi:10.36505/ExLing-2020/11/0047/000462. ISBN 978-618-84585-1-2.
- ^ Léon Brillouin, La science et la théorie de l'information, 1959, réédité en 1988, traduction anglaise rééditée en 2004
- ^ Mitzenmacher, Michael (January 2004). "A Brief History of Generative Models for Power Law and Lognormal Distributions". Internet Mathematics. 1 (2): 226–251. doi:10.1080/15427951.2004.10129088. ISSN 1542-7951. S2CID 1671059. Archived from the original on 2023-07-22. Retrieved 2023-07-25.
- ^ Simkin, M. V.; Roychowdhury, V. P. (2011-05-01). "Re-inventing Willis". Physics Reports. 502 (1): 1–35. arXiv:physics/0601192. Bibcode:2011PhR...502....1S. doi:10.1016/j.physrep.2010.12.004. ISSN 0370-1573. S2CID 88517297. Archived from the original on 2012-01-29. Retrieved 2023-07-25.
- ^ Wentian Li (1992). "Random Texts Exhibit Zipf's-Law-Like Word Frequency Distribution". IEEE Transactions on Information Theory. 38 (6): 1842–1845. CiteSeerX 10.1.1.164.8422. doi:10.1109/18.165464.
- ^ Belevitch V (18 December 1959). "On the statistical laws of linguistic distributions" (PDF). Annales de la Société Scientifique de Bruxelles. 73: 310–326. Archived (PDF) from the original on 15 December 2020. Retrieved 24 April 2020.
- ^ Neumann, Peter G. "Statistical metalinguistics and Zipf/Pareto/Mandelbrot", SRI International Computer Science Laboratory, accessed and archived 29 May 2011.
- ^ Ramon Ferrer i Cancho & Ricard V. Sole (2003). "Least effort and the origins of scaling in human language". Proceedings of the National Academy of Sciences of the United States of America. 100 (3): 788–791. Bibcode:2003PNAS..100..788C. doi:10.1073/pnas.0335980100. PMC 298679. PMID 12540826.
- ^ Conrad, B.; Mitzenmacher, M. (July 2004). "Power laws for monkeys typing randomly: the case of unequal probabilities". IEEE Transactions on Information Theory. 50 (7): 1403–1414. doi:10.1109/TIT.2004.830752. ISSN 1557-9654. S2CID 8913575. Archived from the original on 2022-10-17. Retrieved 2023-08-20.
- ^ Lin, Ruokuang; Ma, Qianli D. Y.; Bian, Chunhua (2014). "Scaling laws in human speech, decreasing emergence of new words and a generalized model". arXiv:1412.4846 [cs.CL].
- ^ Vitanov, Nikolay K.; Ausloos, Marcel; Bian, Chunhua (2015). "Test of two hypotheses explaining the size of populations in a system of cities". Journal of Applied Statistics. 42 (12): 2686–2693. arXiv:1506.08535. Bibcode:2015JApSt..42.2686V. doi:10.1080/02664763.2015.1047744. S2CID 10599428.
- ^ Ricardo T. Fernholz; Robert Fernholz (December 2020). "Zipf's law for atlas models". Journal of Applied Probability. 57 (4): 1276–1297. doi:10.1017/jpr.2020.64. S2CID 146808080. Archived from the original on 2021-01-29. Retrieved 2021-03-26.
- ^ Terence Tao (2012). "E Pluribus Unum: From Complexity, Universality". Daedalus. 141 (3): 23–34. doi:10.1162/DAED_a_00158. S2CID 14535989. Archived from the original on 2021-08-05. Retrieved 2021-03-26.
- ^ N. L. Johnson; S. Kotz & A. W. Kemp (1992). Univariate Discrete Distributions (second ed.). New York: John Wiley & Sons, Inc. ISBN 978-0-471-54897-3., p. 466.
- ^ a b Johan Gerard van der Galien (2003-11-08). "Factorial randomness: the Laws of Benford and Zipf with respect to the first digit distribution of the factor sequence from the natural numbers". Archived from the original on 2007-03-05. Retrieved 8 July 2016.
- ^ Eftekhari, Ali (2006). "Fractal geometry of texts: An initial application to the works of Shakespeare". Journal of Quantitative Linguistic. 13 (2–3): 177–193. doi:10.1080/09296170600850106. S2CID 17657731.
- ^ Pietronero, L.; Tosatti, E.; Tosatti, V.; Vespignani, A. (2001). "Explaining the uneven distribution of numbers in nature: The laws of Benford and Zipf". Physica A. 293 (1–2): 297–304. arXiv:cond-mat/9808305. Bibcode:2001PhyA..293..297P. doi:10.1016/S0378-4371(00)00633-6.
- ^ Gabaix, Xavier (1999). "Zipf's Law for Cities: An Explanation". The Quarterly Journal of Economics. 114 (3): 739–767. doi:10.1162/003355399556133. ISSN 0033-5533. JSTOR 2586883. Archived from the original on 2021-10-26. Retrieved 2021-10-26.
- ^ Arshad, Sidra; Hu, Shougeng; Ashraf, Badar Nadeem (2018-02-15). "Zipf's law and city size distribution: A survey of the literature and future research agenda". Physica A: Statistical Mechanics and Its Applications. 492: 75–92. Bibcode:2018PhyA..492...75A. doi:10.1016/j.physa.2017.10.005. ISSN 0378-4371. Archived from the original on 2023-10-29. Retrieved 2021-10-26.
- ^ Gan, Li; Li, Dong; Song, Shunfeng (2006-08-01). "Is the Zipf law spurious in explaining city-size distributions?". Economics Letters. 92 (2): 256–262. doi:10.1016/j.econlet.2006.03.004. ISSN 0165-1765. Archived from the original on 2019-04-13. Retrieved 2021-10-26.
- ^ Verbavatz, Vincent; Barthelemy, Marc (November 2020). "The growth equation of cities". Nature. 587 (7834): 397–401. arXiv:2011.09403. Bibcode:2020Natur.587..397V. doi:10.1038/s41586-020-2900-x. ISSN 1476-4687. PMID 33208958. S2CID 227012701. Archived from the original on 2021-10-29. Retrieved 2021-10-26.
- ^ Moreno-Sánchez, I.; Font-Clos, F.; Corral, A. (2016). "Large-scale analysis of Zipf's Law in English texts". PLOS ONE. 11 (1): e0147073. arXiv:1509.04486. Bibcode:2016PLoSO..1147073M. doi:10.1371/journal.pone.0147073. PMC 4723055. PMID 26800025.
- ^ Mohammadi, Mehdi (2016). "Parallel Document Identification using Zipf's Law" (PDF). Proceedings of the Ninth Workshop on Building and Using Comparable Corpora. LREC 2016. Portorož, Slovenia. pp. 21–25. Archived (PDF) from the original on 2018-03-23.
- ^ Doyle, Laurance R. (2016-11-18). "Why Alien Language Would Stand Out Among All the Noise of the Universe". Nautilus Quarterly. Archived from the original on 2020-07-29. Retrieved 2020-08-30.
- ^ Kershenbaum, Arik (2021-03-16). The Zoologist's Guide to the Galaxy: What Animals on Earth Reveal About Aliens--and Ourselves. Penguin. pp. 251–256. ISBN 978-1-9848-8197-7. OCLC 1242873084.
- ^ Frans J. Van Droogenbroeck (2016): Handling the Zipf distribution in computerized authorship attribution Archived 2023-10-04 at the Wayback Machine
- ^ Frans J. Van Droogenbroeck (2019): An essential rephrasing of the Zipf-Mandelbrot law to solve authorship attribution applications by Gaussian statistics Archived 2023-09-30 at the Wayback Machine
- ^ Boyle, Rebecca. "Mystery text's language-like patterns may be an elaborate hoax". New Scientist. Archived from the original on 2022-05-18. Retrieved 2022-02-25.
- ^ Montemurro, Marcelo A.; Zanette, Damián H. (2013-06-21). "Keywords and Co-Occurrence Patterns in the Voynich Manuscript: An Information-Theoretic Analysis". PLOS ONE. 8 (6): e66344. Bibcode:2013PLoSO...866344M. doi:10.1371/journal.pone.0066344. ISSN 1932-6203. PMC 3689824. PMID 23805215.
Further reading
[edit]- Alexander Gelbukh and Grigori Sidorov (2001) "Zipf and Heaps Laws’ Coefficients Depend on Language". Proc. CICLing-2001, Conference on Intelligent Text Processing and Computational Linguistics, February 18–24, 2001, Mexico City. Lecture Notes in Computer Science N 2004, ISSN 0302-9743, ISBN 3-540-41687-0, Springer-Verlag: 332–335.
- Kali R. (2003) "The city as a giant component: a random graph approach to Zipf's law," Applied Economics Letters 10: 717–720(4)
- Shyklo A. (2017); Simple Explanation of Zipf's Mystery via New Rank-Share Distribution, Derived from Combinatorics of the Ranking Process, Available at SSRN: https://ssrn.com/abstract=2918642.
- Clara Moskowitz, Jen Christiansen, and Ni-Ka Ford, "Cells by Count and Size: The larger a cell type is, the rarer it is in the body – and vice versa", Scientific American, vol. 330, no. 1 (January 2024), pp. 94–95. "'As you double the volume of a cell, the frequency of cells of that size is halved,'" ecologist Ian A. Hatton of McGill University and his fellow Zipf's-law researchers found, says Hatton. "Teensy, nonnucleated red blood cells are by far the most common cells in our bodies, whereas the comparatively gigantic muscle cells in our arms and legs are the scarcest. Being able to use a cell's size to estimate its frequency in the body could help doctors better understand certain body systems and hard-to-count cell types... The study suggests, for instance, that immune cells called lymphocytes are far more common than biologists realized." (p. 94.)
External links
[edit]- Strogatz, Steven (2009-05-29). "Guest Column: Math and the City". The New York Times. Archived from the original on 2015-09-27. Retrieved 2009-05-29.—An article on Zipf's law applied to city populations
- Seeing Around Corners (Artificial societies turn up Zipf's law)
- PlanetMath article on Zipf's law
- Distributions de type "fractal parabolique" dans la Nature (French, with English summary) Archived 2004-10-24 at the Wayback Machine
- An analysis of income distribution
- Zipf List of French words Archived 2007-06-23 at the Wayback Machine
- Zipf list for English, French, Spanish, Italian, Swedish, Icelandic, Latin, Portuguese and Finnish from Gutenberg Project and online calculator to rank words in texts Archived 2011-04-08 at the Wayback Machine
- Citations and the Zipf–Mandelbrot's law
- Zipf's Law examples and modelling (1985)
- Complex systems: Unzipping Zipf's law (2011)
- Benford’s law, Zipf’s law, and the Pareto distribution by Terence Tao.
- "Zipf law", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
























![{\displaystyle f(k;\rho )\approx {\frac {[{\text{constant}}]}{k^{\rho +1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78fb2a5a8523f03c5e11716e40fd9627c18ff49f)