Q-Weibull distribution

q-Weibull distribution

Probability density function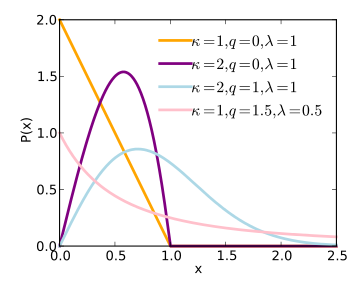
Cumulative distribution function
Parameters	$q<2$ shape (real) $\lambda >0$ rate (real) $\kappa >0\,$ shape (real)
Support	$x\in [0;+\infty )\!{\text{ for }}q\geq 1$ $x\in [0;{\lambda \over {(1-q)^{1/\kappa }}}){\text{ for }}q<1$
PDF	${\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}^{-(x/\lambda )^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
CDF	${\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$
Mean	(see article)

In statistics, the q-Weibull distribution is a probability distribution that generalizes the Weibull distribution and the Lomax distribution (Pareto Type II). It is one example of a Tsallis distribution.

Characterization

Probability density function

The probability density function of a q-Weibull random variable is:

$f(x;q,\lambda ,\kappa )={\begin{cases}(2-q){\frac {\kappa }{\lambda }}\left({\frac {x}{\lambda }}\right)^{\kappa -1}e_{q}^{-(x/\lambda )^{\kappa }}&x\geq 0,\\0&x<0,\end{cases}}$

where q < 2, $\kappa$ > 0 are shape parameters and λ > 0 is the scale parameter of the distribution and

$e_{q}(x)={\begin{cases}(1+(1-q)x)^{\frac {1}{1-q}}&q\neq 1,1+(1-q)x>0\\0&q\neq 1,1+(1-q)x\leq 0\\e^{x}&q=1\end{cases}}$

is the q-exponential

Cumulative distribution function

The cumulative distribution function of a q-Weibull random variable is:

${\begin{cases}1-e_{q'}^{-(x/\lambda ')^{\kappa }}&x\geq 0\\0&x<0\end{cases}}$

where

$\lambda '={\lambda \over (2-q)^{1 \over \kappa }}$

$q'={1 \over (2-q)}$

Mean

The mean of the q-Weibull distribution is

$\mu (q,\lambda ,\kappa )={\begin{cases}\lambda \,(2-q)(1-q)^{-{\frac {1+\kappa }{\kappa }}}\,B[1+{\frac {1}{\kappa }},{\frac {2-q}{1-q}}]&0\leq q<1\\\lambda \,\Gamma (1+{\frac {1}{\kappa }})&q=1\\\lambda \,(2-q)(q-1)^{-{\frac {1+\kappa }{\kappa }}}\,B[1+{\frac {1}{\kappa }},{\frac {1}{q-1}}-{\frac {1+\kappa }{\kappa }}]&1<q<1+{\frac {\kappa }{\kappa +1}}\\\infty &1+{\frac {\kappa }{\kappa +1}}\leq q<2\end{cases}}$

where $B()$ is the Beta function and $\Gamma ()$ is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.

Relationship to other distributions

The q-Weibull is equivalent to the Weibull distribution when q = 1 and equivalent to the q-exponential when $\kappa =1$

The q-Weibull is a generalization of the Weibull, as it extends this distribution to the cases of finite support (q < 1) and to include heavy tail distributions $(q\geq 1+{\frac {\kappa }{\kappa +1}})$.

The q-Weibull is a generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support and adds the $\kappa$ parameter. The Lomax parameters are:

$\alpha ={{2-q} \over {q-1}}~,~\lambda _{\text{Lomax}}={1 \over {\lambda (q-1)}}$

As the Lomax distribution is a shifted version of the Pareto distribution, the q-Weibull for $\kappa =1$ is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:

${\text{If }}X\sim \mathrm {qWeibull} (q,\lambda ,\kappa =1){\text{ and }}Y\sim \left[{\text{Pareto}}\left(x_{m}={1 \over {\lambda (q-1)}},\alpha ={{2-q} \over {q-1}}\right)-x_{m}\right],{\text{ then }}X\sim Y\,$

See also

• Constantino Tsallis
• Tsallis statistics
• Tsallis entropy
• Tsallis distribution
• q-Gaussian