Property (philosophy)
In logic and philosophy (especially metaphysics), a property is a characteristic of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property, however, differs from individual objects in that it may be instantiated, and often in more than one object. It differs from the logical/mathematical concept of class by not having any concept of extensionality, and from the philosophical concept of class in that a property is considered to be distinct from the objects which possess it. Understanding how different individual entities (or particulars) can in some sense have some of the same properties is the basis of the problem of universals.
Terms and usage[edit]
A property is any member of a class of entities that are capable of being attributed to objects. Terms similar to property include predicable, attribute, quality, feature, characteristic, type, exemplifiable, predicate, and intensional entity.[1]
Generally speaking, an object is said to exemplify, instantiate, bear, have or possess a property if the property can be truly predicated of the object. The collection of objects that possess a property is called the extension of the property. Properties are said to characterize or inhere in objects that possess them.[1] Followers of Alexius Meinong assert the existence of two kinds of predication: existent objects exemplify properties, while nonexistent objects are said to exemplify, satisfy, immanently contain or be consubstantiated by properties that are actually possessed and are said to encode, be determined by, be consociated with or be constituted by properties that are merely ascribed to objects. For example, since Pegasus is merely mythical, Pegasus encodes the property of being a horse, but Pegasus exemplifies the property of being a character of Greek mythology as well.[2] Edward Jonathan Lowe even treated instantiation, characterization and exemplification as three separate kinds of predication.[1]
Broadly construed, examples of properties include redness, the property of being two,[3] the property of being nonexistent,[4] the property of being identical to Socrates,[1] the property of being a desk,[1] the property of being a property,[1] the property of being both round and square,[1] and the property of being heterological. Some philosophers refuse to treat existence as a property, and Peter van Inwagen suggested that one should deny the existence of certain "properties" so as to avoid paradoxes such as Russell's paradox and Grelling–Nelson paradox, though such moves remain controversial.[1]
Metaphysical debates[edit]
In modern analytic philosophy there are several debates about the fundamental nature of properties. These center around questions such as: Are properties universals or particulars? Are properties real? Are they categorical or dispositional? Are properties physical or mental?
Universals vs. particulars[edit]
At least since Plato, properties are viewed by numerous philosophers as universals, which are typically capable of being instantiated by different objects. Philosophers opposing this view regard properties as particulars, namely tropes.[1]
Realism vs. anti-realism[edit]
A realist about properties asserts that properties have genuine, mind-independent existence.[1] One way to spell this out is in terms of exact, repeatable, instantiations known as universals. The other realist position asserts that properties are particulars (tropes), which are unique instantiations in individual objects that merely resemble one another to various degrees. Transcendent realism, proposed by Plato and favored by Bertrand Russell, asserts that properties exist even if uninstantiated.[1] Immanent realism, defended by Aristotle and David Malet Armstrong, contends that properties exist only if instantiated.[1]
The anti-realist position, often referred to as nominalism claims that properties are names we attach to particulars. The properties themselves have no existence.
Categoricalism vs. dispositionalism[edit]
Properties are often classified as either categorical and dispositional.[5][6] Categorical properties concern what something is like, e.g. what qualities it has. Dispositional properties, on the other hand, involve what powers something has, what it is able to do, even if it is not actually doing it.[5] For example, the shape of a sugar cube is a categorical property while its tendency to dissolve in water is a dispositional property. For many properties there is a lack of consensus as to how they should be classified, for example, whether colors are categorical or dispositional properties.[7][8]
According to categoricalism, dispositions reduce to causal bases.[9] On this view, the fragility of a wine glass, a dispositional property, is not a fundamental feature of the glass since it can be explained in terms of the categorical property of the glass's micro-structural composition. Dispositionalism, on the other hand, asserts that a property is nothing more than a set of causal powers.[7] Fragility, according to this view, identifies a real property of the glass (e.g. to shatter when dropped on a sufficiently hard surface). Several intermediary positions exist.[7] The Identity view states that properties are both categorical (qualitative) and dispositional; these are just two ways of viewing the same property. One hybrid view claims that some properties are categorical and some are dispositional. A second hybrid view claims that properties have both a categorical (qualitative) and dispositional part, but that these are distinct ontological parts.
Physicalism, idealism, and property dualism[edit]
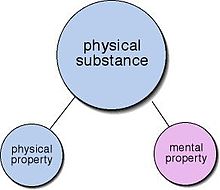
Property dualism describes a category of positions in the philosophy of mind which hold that, although the world is constituted of just one kind of substance—the physical kind—there exist two distinct kinds of properties: physical properties and mental properties. In other words, it is the view that non-physical, mental properties (such as beliefs, desires and emotions) inhere in some physical substances (namely brains).
This stands in contrast to physicalism and idealism. Physicalism claims that all properties, include mental properties, ultimately reduce to, or supervene on, physical properties.[10] Metaphysical idealism, by contrast, claims that "something mental (the mind, spirit, reason, will) is the ultimate foundation of all reality, or even exhaustive of reality."[11]
Types[edit]
Intrinsic and extrinsic[edit]
An intrinsic property is a property that an object or a thing has of itself, independently of other things, including its context. An extrinsic (or relational) property is a property that depends on a thing's relationship with other things. The latter is sometimes also called an attribute, since the value of that property is given to the object via its relation with another object. For example, mass is a physical intrinsic property of any physical object, whereas weight is an extrinsic property that varies depending on the strength of the gravitational field in which the respective object is placed. Another example of a relational property is the name of a person (an attribute given by the person's parents).
Essential and accidental[edit]
In classical Aristotelian terminology, a property (Greek: idion, Latin: proprium) is one of the predicables. It is a non-essential quality of a species (like an accident), but a quality which is nevertheless characteristically present in members of that species. For example, "ability to laugh" may be considered a special characteristic of human beings. However, "laughter" is not an essential quality of the species human, whose Aristotelian definition of "rational animal" does not require laughter. Therefore, in the classical framework, properties are characteristic qualities that are not truly required for the continued existence of an entity but are, nevertheless, possessed by the entity.
Determinate and determinable[edit]
A property may be classified as either determinate or determinable. A determinable property is one that can get more specific. For example, color is a determinable property because it can be restricted to redness, blueness, etc.[12] A determinate property is one that cannot become more specific. This distinction may be useful in dealing with issues of identity.[13]
Pure and impure[edit]
Impure properties are properties that, unlike pure properties, involve reference to a particular substance in their definition.[14] So, for example, being a wife is a pure property while being the wife of Socrates is an impure property due to the reference to the particular "Socrates".[15] Sometimes, the terms qualitative and non-qualitative are used instead of pure and impure.[16] Most but not all impure properties are extrinsic properties. This distinction is relevant for the principle of identity of indiscernibles, which states that two things are identical if they are indiscernible, i.e. if they share all their properties.[14] This principle is usually defined in terms of pure properties only. The reason for this is that impure properties are not relevant for similarity or discernibility but taking them into consideration nonetheless would result in the principle being trivially true.[14] Another application of this distinction concerns the problem of duplication, for example, in the Twin Earth thought experiment. It is usually held that duplication only involves qualitative identity but perfect duplicates can still differ concerning their non-qualitative or impure properties.[16]
Lovely and suspect[edit]
Daniel Dennett distinguishes between lovely properties (such as loveliness itself), which, although they require an observer to be recognised, exist latently in perceivable objects; and suspect properties which have no existence at all until attributed by an observer (such as being suspected of a crime).[17]
Properties and predicates[edit]
The ontological fact that something has a property is typically represented in language by applying a predicate to a subject. However, taking any grammatical predicate whatsoever to be a property, or to have a corresponding property, leads to certain difficulties, such as Russell's paradox and the Grelling–Nelson paradox. Moreover, a real property can imply a host of true predicates: for instance, if X has the property of weighing more than 2 kilos, then the predicates "..weighs more than 1.9 kilos", "..weighs more than 1.8 kilos", etc., are all true of it. Other predicates, such as "is an individual", or "has some properties" are uninformative or vacuous. There is some resistance to regarding such so-called "Cambridge properties" as legitimate.[18] These properties in the widest sense are sometimes referred to as abundant properties. They are contrasted with sparse properties, which include only properties "responsible for the objective resemblances and causal powers of things".[19]
Role in similarity[edit]
The traditional conception of similarity holds that properties are responsible for similarity: two objects are similar because they have a property in common. The more properties they share, the more similar they are. They resemble each other exactly if they share all their properties.[20][21] For this conception of similarity to work, it is important that only properties relevant to resemblance are taken into account, sometimes referred to as sparse properties in contrast to abundant properties.[22][19]
Relations[edit]
The distinction between properties and relations can hardly be given in terms that do not ultimately presuppose it.[23]
Relations are true of several particulars, or shared amongst them. Thus the relation "... is taller than ..." holds "between" two individuals, who would occupy the two ellipses ('...'). Relations can be expressed by N-place predicates, where N is greater than 1.
Relations should be distinguished from relational properties. For example, marriage is a relation since it is between two people, but being married to X is a relational property had by a certain person since it concerns only one person.[23]
There are at least some apparent relational properties which are merely derived from non-relational (or 1-place) properties. For instance "A is heavier than B" is a relational predicate, but it is derived from the two non relational properties: the mass of A and the mass of B. Such relations are called external relations, as opposed to the more genuine internal relations.[24] Some philosophers believe that all relations are external, leading to a scepticism about relations in general, on the basis that external relations have no fundamental existence.[citation needed]
See also[edit]
- Abstraction
- Autological word
- Bradley's regress, a relevant philosophical problem
- Doctrine of internal relations
- Emergent properties
- Grelling–Nelson paradox
- Identity of indiscernibles (or "Leibniz's law")
- Intension
- Opposite (semantics)
- Property (mathematics)
- Russell's paradox
- Similarity (philosophy)
References[edit]
- ^ a b c d e f g h i j k l "Properties". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.
- ^ Reicher, Maria. "Nonexistent Objects". The Stanford Encyclopedia of Philosophy (Winter 2019 Edition), Edward N. Zalta (ed.). Retrieved 25 March 2021.
- ^ Yi, Byeong-uk (April 1999). "Is Two a Property?" (PDF). Journal of Philosophy. 96 (4): 163–190. doi:10.2307/2564701. JSTOR 2564701. Retrieved 25 March 2021.
- ^ Berto, Francesco (2012). Existence as a Real Property: The Ontology of Meinongianism. Springer Science & Business Media. p. 130. ISBN 978-9400742062.
- ^ a b Borchert, Donald (2006). "Ontology". Macmillan Encyclopedia of Philosophy, 2nd Edition. Macmillan.
- ^ Kriegel, Uriah (2019). "Introverted Metaphysics: How We Get Our Grip on the Ultimate Nature of Objects, Properties, and Causation". Metaphilosophy. 50 (5): 688–707. doi:10.1111/meta.12391. S2CID 211938090.
- ^ a b c Choi, Sungho; Fara, Michael (2018). "Dispositions". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Rubenstein, Eric M. "Color". Internet Encyclopedia of Philosophy. Retrieved 7 January 2021.
- ^ "Properties". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.
- ^ "Physicalism". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.
- ^ "Idealism". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2018.
- ^ Stanford Encyclopaedia of Philosophy Determinate and Determinable Properties
- ^ Georges Dicker (1998). Hume's Epistemology & Metaphysics. Routledge. p. 31.
- ^ a b c Forrest, Peter (2020). "The Identity of Indiscernibles: 1. Formulating the Principle". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 25 January 2021.
- ^ Rosenkrantz, Gary S. (1979). "The Pure and the Impure". Logique et Analyse. 22 (88): 515–523. ISSN 0024-5836. JSTOR 44085165.
- ^ a b Cowling, Sam (2015). "Non-Qualitative Properties". Erkenntnis. 80 (2): 275–301. doi:10.1007/s10670-014-9626-9. S2CID 254472503.
- ^ "Lovely and Suspect Qualities". Retrieved 3 August 2016.
- ^ Nelson, Michael (1 January 2012). Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy. Retrieved 3 August 2016 – via Stanford Encyclopedia of Philosophy.
- ^ a b Orilia, Francesco; Paolini Paoletti, Michele (2020). "Properties". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Allen, Sophie. "Properties". Internet Encyclopedia of Philosophy. Retrieved 19 January 2021.
- ^ Tversky, Amos (1977). "Features of Similarity". Psychological Review. 84 (4): 327–352. doi:10.1037/0033-295X.84.4.327.
- ^ Blumson, Ben (2018). "Two Conceptions of Similarity". Philosophical Quarterly. 68 (270): 21–37. doi:10.1093/pq/pqx021.
- ^ a b MacBride, Fraser. "Relations". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ^ G. E. Moore (December 15, 1919), "External and Internal Relations"
External links[edit]
- Zalta, Edward N. (ed.). "Properties". Stanford Encyclopedia of Philosophy.
- MacBride, Fraser. "Relations". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
