Lossless JPEG
Lossless JPEG is a 1993 addition to JPEG standard by the Joint Photographic Experts Group to enable lossless compression. However, the term may also be used to refer to all lossless compression schemes developed by the group, including JPEG 2000, JPEG-LS, and JPEG XL.
Lossless JPEG was developed as a late addition to JPEG in 1993, using a completely different technique from the lossy JPEG standard. It uses a predictive scheme based on the three nearest (causal) neighbors (upper, left, and upper-left), and entropy coding is used on the prediction error. The standard Independent JPEG Group libraries cannot encode or decode it, but Ken Murchison of Oceana Matrix Ltd. wrote a patch that extends the IJG library to handle lossless JPEG.[1] Lossless JPEG has some popularity in medical imaging, and is used in DNG and some digital cameras to compress raw images, but otherwise was never widely adopted. Adobe's DNG SDK provides a software library for encoding and decoding lossless JPEG with up to 16 bits per sample.
ISO/IEC Joint Photography Experts Group maintains a reference software implementation which can encode both base JPEG (ISO/IEC 10918-1 and 18477-1) and JPEG XT extensions (ISO/IEC 18477 Parts 2 and 6-9), as well as JPEG-LS (ISO/IEC 14495).[2]
Lossless mode of operation
[edit]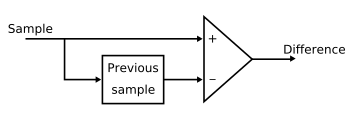


Lossless JPEG[3] is actually a mode of operation of JPEG. This mode exists because the discrete cosine transform (DCT) based form cannot guarantee that encoder input would exactly match decoder output. Unlike the lossy mode which is based on the DCT, the lossless coding process employs a simple predictive coding model called differential pulse-code modulation (DPCM). This is a model in which predictions of the sample values are estimated from the neighboring samples that are already coded in the image. Most predictors take the average of the samples immediately above and to the left of the target sample. DPCM encodes the differences between the predicted samples instead of encoding each sample independently. The differences from one sample to the next are usually close to zero. A typical DPCM encoder is displayed in Fig.1. The block in the figure acts as a storage of the current sample which will later be a previous sample.
The main steps of lossless operation mode are depicted in Fig.2. In the process, the predictor combines up to three neighboring samples at A, B, and C shown in Fig.3 in order to produce a prediction of the sample value at the position labeled by X. The three neighboring samples must be already encoded samples. Any one of the predictors shown in the table below can be used to estimate the sample located at X.[4] Any one of the eight predictors listed in the table can be used. Note that selections 1, 2, and 3 are one-dimensional predictors and selections 4, 5, 6, and 7 are two-dimensional predictors. The first selection value in the table, zero, is only used for differential coding in the hierarchical mode of operation. Once all the samples are predicted, the differences between the samples can be obtained and entropy-coded in a lossless fashion using Huffman coding or arithmetic coding.
| Selection-value | Prediction |
|---|---|
| 0 | No prediction |
| 1 | A |
| 2 | B |
| 3 | C |
| 4 | A + B – C |
| 5 | A + (B – C)/2 |
| 6 | B + (A – C)/2 |
| 7 | (A + B)/2 |
Typically, compressions using lossless operation mode can achieve around 2:1 compression ratio for color images.[5] This mode is quite popular in the medical imaging field, and defined as an option in DNG standard, but otherwise it is not very widely used because of complexity of doing arithmetics on 10, 12, or 14bpp values on typical embedded 32-bit processor and a little resulting gain in space.[citation needed]
JPEG-LS
[edit]General description
[edit]JPEG-LS is a lossless or near-lossless compression standard for continuous-tone images.[6] Its official designation is ISO-14495-1/ITU-T.87.[7] It is a simple and efficient baseline algorithm which consists of two independent and distinct stages called modeling and encoding. JPEG-LS was developed with the aim of providing a low-complexity lossless and near-lossless image compression standard that could offer better compression efficiency than lossless JPEG. It was developed because at the time, the Huffman coding-based JPEG lossless standard and other standards were limited in their compression performance. Total decorrelation cannot be achieved by first order entropy of the prediction residuals employed by these inferior standards. JPEG-LS, on the other hand, can obtain good decorrelation.[8][9] Part 1 of this standard was finalized in 1999. Part 2, released in 2003, introduced extensions such as arithmetic coding. The core of JPEG-LS is based on the LOCO-I algorithm,[10] that relies on prediction, residual modeling, and context-based coding of the residuals. Most of the low complexity of this technique comes from the assumption that prediction residuals follow a two-sided geometric distribution (also called a discrete Laplace distribution) and from the use of Golomb-like codes, which are known to be approximately optimal for geometric distributions. Besides lossless compression, JPEG-LS also provides a lossy mode ("near-lossless") where the maximum absolute error can be controlled by the encoder.
Performance
[edit]- Compression for JPEG-LS is generally much faster than JPEG 2000 and much better than the original lossless JPEG standard.
- Compression for JPEG-LS is generally slightly worse than JPEG 2000, but this highly depends on the image content.
- Decompression for JPEG-LS is generally much faster than JPEG 2000, but this depends on the exact software decoder implementations.
- This statement is valid for open-source implementations.
Application support
[edit]- IrfanView image viewer and editor has full read+write support for JPEG-LS image codec (.jls file extension).
- XnView image viewer and editor claims the capability to read JPEG-LS (.jls) files.
- However, XnViewMP v0.98.1 can not read JPEG-LS files created by IrfanView v4.54.
- CharLS - an open-source JPEG-LS codec.
- Thomas Richter's libjpeg - an open-source JPEG-LS codec.
- UBC JPEG-LS codec
- David Clunie's JPEG-LS codec
- Hewlett-Packard JPEG-LS reference encoder v1.00 (direct link to zipfile)
LOCO-I algorithm
[edit]Prior to encoding, there are two essential steps to be done in the modeling stage: decorrelation (prediction) and error modeling.
Decorrelation/prediction
[edit]In the LOCO-I algorithm, primitive edge detection of horizontal or vertical edges is achieved by examining the neighboring pixels of the current pixel X as illustrated in Fig.3. The pixel labeled by B is used in the case of a vertical edge while the pixel located at A is used in the case of a horizontal edge. This simple predictor is called the Median Edge Detection (MED) predictor[11] or LOCO-I predictor. The pixel X is predicted by the LOCO-I predictor according to the following guesses:
The three simple predictors are selected according to the following conditions: (1) it tends to pick B in cases where a vertical edge exists left of the X, (2) A in cases of an horizontal edge above X, or (3) A + B – C if no edge is detected.
Context modeling
[edit]The JPEG-LS algorithm estimates the conditional expectations of the prediction errors using corresponding sample means within each context Ctx. The purpose of context modeling is that the higher order structures like texture patterns and local activity of the image can be exploited by context modeling of the prediction error. Contexts are determined by obtaining the differences of the neighboring samples which represents the local gradient:
The local gradient reflects the level of activities such as smoothness and edginess of the neighboring samples. Notice that these differences are closely related to the statistical behavior of prediction errors. Each one of the differences found in the above equation is then quantized into roughly equiprobable and connected regions. For JPEG-LS, the differences g1, g2, and g3 are quantized into 9 regions and the region are indexed from −4 to 4. The purpose of the quantization is to maximize the mutual information between the current sample value and its context such that the high-order dependencies can be captured. One can obtain the contexts based on the assumption that
After merging contexts of both positive and negative signs, the total number of contexts is contexts. A bias estimation could be obtained by dividing cumulative prediction errors within each context by a count of context occurrences. In LOCO-I algorithm, this procedure is modified and improved such that the number of subtractions and additions are reduced. The division-free bias computation procedure is demonstrated in [2]. Prediction refinement can then be done by applying these estimates in a feedback mechanism which eliminates prediction biases in different contexts.
Coding corrected prediction residuals
[edit]In the regular mode of JPEG-LS, the standard uses Golomb–Rice codes which are a way to encode non-negative run lengths. Its special case with the optimal encoding value 2k allows simpler encoding procedures.
Run length coding in uniform areas
[edit]Since Golomb–Rice codes are quite inefficient for encoding low entropy distributions because the coding rate is at least one bit per symbol, significant redundancy may be produced because the smooth regions in an image can be encoded at less than 1 bit per symbol. To avoid having excess code length over the entropy, one can use alphabet extension which codes blocks of symbols instead of coding individual symbols. This spreads out the excess coding length over many symbols. This is the “run” mode of JPEG-LS and it is executed once a flat or smooth context region characterized by zero gradients is detected. A run of west symbol “a” is expected and the end of run occurs when a new symbol occurs or the end of line is reached. The total run of length is encoded and the encoder would return to the “regular” mode.
JPEG 2000
[edit]JPEG 2000 includes a lossless mode based on a special integer wavelet filter (biorthogonal 3/5). JPEG 2000's lossless mode runs more slowly and has often worse compression ratios than JPEG-LS on artificial and compound images[12][13] but fares better than the UBC implementation of JPEG-LS on digital camera pictures.[14] JPEG 2000 is also scalable, progressive, and more widely implemented.[citation needed]
JPEG XT
[edit]JPEG XT includes a lossless integer-to-integer DCT transform mode based on wavelet compression from JPEG 2000.[citation needed]
JPEG XL
[edit]JPEG XL includes a lossless/near-lossless/responsive mode called Modular which optionally uses a modified Haar transform (called "squeeze") and which is also used to encode the DC (1:8 scale) image in VarDCT mode as well as various auxiliary images such as adaptive quantization fields or additional channels like alpha.[15]
References
[edit]- ^ Murchison, Ken (April 4, 1999). "Lossless JPEG support for libjpeg". Newsgroup: comp.protocols.dicom. Usenet: 372618DE.969A19D9@oceana.com. Retrieved December 12, 2017.
A number of people have been interested in my patch which adds lossless JPEG support (per the original spec -- not JPEG-LS) to libjpeg v6b. I have decided to make this patch available via my ftp site (ftp://ftp.oceana.com/pub/ljpeg-6b.tar.gz).
{{cite newsgroup}}: External link in|quote= - ^ "JPEG - JPEG XT". jpeg.org.
- ^ Pennebaker, W. B. & Mitchell, J. L. (1993). JPEG Still Image Data Compression Standard. New York: Van Nostrand Reinhold. ISBN 978-0-442-01272-4.
- ^ ITU-T. ISO DIS 10918-1 Digital compression and coding of continuous-tone still images (JPEG). Recommendation T.81.
- ^ Wallace, C. K. (1991). "The JPEG still picture compression standard". Communications of the ACM. 34 (4): 31–44. CiteSeerX 10.1.1.318.4292. doi:10.1109/30.125072.
- ^ "HP Labs LOCO-I/JPEG-LS Home Page". Hewlett-Packard Development Company. May 13, 2005. Retrieved 24 October 2011.
- ^ "T.87: Information technology – Lossless and near-lossless compression of continuous-tone still images – Baseline". International Telecommunication Union. Retrieved 24 October 2011.
- ^ M. J. Weinberger, G. Seroussi, and G. Sapiro, “LOCO-I: A low complexity, context-based, lossless image compression algorithm,” in Proc. 1996 Data Compression Conference, Snowbird, UT, Mar. 1996, pp. 140–149.
- ^ M. Weinberger, G. Seroussi, and G. Sapiro, “The LOCO-I lossless image compression algorithm: Principles and standardization into JPEG-LS,” IEEE Trans. Image Processing, vol. 9, no. 8, pp. 1309–1324, Aug. 2000, originally as Hewlett-Packard Laboratories Technical Report No. HPL-98-193R1, November 1998, revised October 1999. Available from [1].
- ^ http://www.hpl.hp.com/loco/HPL-98-193R1.pdf Archived 2019-12-26 at the Wayback Machine LOCO-I algorithm
- ^ Memon, Nasir D.; Wu, Xiaolin; Sippy, V. & Miller, G. (1997). "Interband coding extension of the new lossless JPEG standard". In Biemond, Jan & Delp Iii, Edward J. (eds.). Visual Communications and Image Processing '97. Proceedings of SPIE. Vol. 3024. pp. 47–58. Bibcode:1997SPIE.3024...47M. doi:10.1117/12.263270. S2CID 58232715.
- ^ "Archived copy" (PDF). Archived from the original (PDF) on 2006-07-02. Retrieved 2006-06-17.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Archived copy". Archived from the original on 2007-02-22. Retrieved 2007-02-07.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Lossless Photo Compression Benchmark". imagecompression.info.
- ^ Alakuijala, Jyrki; van Asseldonk, Ruud; Boukortt, Sami; Szabadka, Zoltan; Bruse, Martin; Comsa, Iulia-Maria; Firsching, Moritz; Fischbacher, Thomas; Kliuchnikov, Evgenii; Gomez, Sebastian; Obryk, Robert; Potempa, Krzysztof; Rhatushnyak, Alexander; Sneyers, Jon; Szabadka, Zoltan; Vandervenne, Lode; Versari, Luca; Wassenberg, Jan (6 September 2019). "JPEG XL next-generation image compression architecture and coding tools". In Tescher, Andrew G; Ebrahimi, Touradj (eds.). Applications of Digital Image Processing XLII. Vol. 11137. p. 20. Bibcode:2019SPIE11137E..0KA. doi:10.1117/12.2529237. ISBN 9781510629677.
External links
[edit]- JPEG 2000 still image coding versus other standards
- JPEG2000, JPEG-LS and other lossless codecs on greyscale images
- JPEG-LS home page
- LOCO-I home page
- HP Labs LOCO-I/JPEG-LS home page
- Licensing terms for HP's LOCO technology in JPEG-LS (free reg. req.; not sublicensable; available only to companies)
- Links to various implementations
- Single-tone/grayscale JPEG-LS encoder algorithm
- Evaluation of JPEG-LS, IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 39, NO. 10, OCTOBER 2001





![{\displaystyle P(e\mid Ctx=[q_{1},q_{2},q_{3}])=P(-e\mid Ctx=[-q_{1},-q_{2},-q_{3}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3741cc09942502e1e2ad212a2c2c5d8eac2dad48)
