Gravity: Difference between revisions
m Reverted edits by 66.253.214.32 (talk) to last version by 121.223.108.200 |
No edit summary |
||
| Line 5: | Line 5: | ||
Modern [[physics]] describes gravitation using the [[general theory of relativity]]. [[Newton's law of universal gravitation]] provides an excellent approximation for most calculations. |
Modern [[physics]] describes gravitation using the [[general theory of relativity]]. [[Newton's law of universal gravitation]] provides an excellent approximation for most calculations. |
||
The terms '''gravitation''' and '''gravity''' are mostly interchangeable in everyday use, but in scientific usage a distinction may be made. "Gravitation" is a general term describing the [[fundamental forces]] of physics responsible for keeping the Earth and the other planets in their [[orbit]]s around the Sun; for keeping the [[Moon]] in its orbit around the Earth, for the formation of [[tides]]; for [[convection]] (by which hot fluids rise); for heating the interiors of forming stars and planets to very high temperatures; and for various other phenomena that we observe. By contrast, in [[general relativity]] |
The terms '''gravitation''' and '''gravity''' are mostly interchangeable in everyday use, but in scientific usage a distinction may be made. "Gravitation" is a general term describing the [[fundamental forces]] of physics responsible for keeping the Earth and the other planets in their [[orbit]]s around the Sun; for keeping the [[Moon]] in its orbit around the Earth, for the formation of [[tides]]; for [[convection]] (by which hot fluids rise); for heating the interiors of forming stars and planets to very high temperatures; and for various other phenomena that we observe. By contrast, in [[general relativity]] gravity is due to spacetime curvatures which cause [[inertia]]lly moving objects to accelerate towards each other. |
||
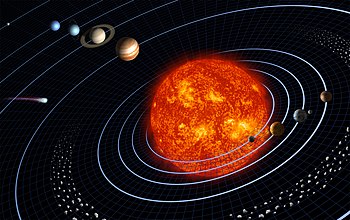
[[Image:Solar sys.jpg|right|350px|thumb|Gravitation keeps the planets in orbit about the Sun. (Not to scale)]] |
[[Image:Solar sys.jpg|right|350px|thumb|Gravitation keeps the planets in orbit about the Sun. (Not to scale)]] |
||
Revision as of 13:14, 18 September 2008
Gravitation is a natural phenomenon by which objects with mass attract one another[1]. In everyday life, gravitation is most commonly thought of as the agency which lends weight to any object. Gravitation compels dispersed matter to coalesce, thus it accounts for the very existence of the Earth, the Sun, and most of the macroscopic objects in the universe.
Modern physics describes gravitation using the general theory of relativity. Newton's law of universal gravitation provides an excellent approximation for most calculations.
The terms gravitation and gravity are mostly interchangeable in everyday use, but in scientific usage a distinction may be made. "Gravitation" is a general term describing the fundamental forces of physics responsible for keeping the Earth and the other planets in their orbits around the Sun; for keeping the Moon in its orbit around the Earth, for the formation of tides; for convection (by which hot fluids rise); for heating the interiors of forming stars and planets to very high temperatures; and for various other phenomena that we observe. By contrast, in general relativity gravity is due to spacetime curvatures which cause inertially moving objects to accelerate towards each other.
History of gravitational theory
Early history
Efforts to understand gravity began in ancient times. Philosophers in ancient India explained the phenomenon from the 8th century BC.[2] According to Kanada, founder of the Vaisheshika school, "Weight causes falling; it is imperceptible and known by inference."[3]
In the 4th century BC, the Greek philosopher Aristotle believed that there was no effect without a cause, and therefore no motion without a force. He hypothesized that everything tried to move towards its proper place in the crystalline spheres of the heavens, and that physical bodies fell toward the center of the Earth in proportion to their weight.
Brahmagupta, in the Brahmasphuta Siddhanta (AD 628), responded to critics of the heliocentric system of Aryabhata (AD 476–550) stating that "all heavy things are attracted towards the center of the earth" and that "all heavy things fall down to the earth by a law of nature, for it is the nature of the earth to attract and to keep things, as it is the nature of water to flow, that of fire to burn, and that of wind to set in motion... The earth is the only low thing, and seeds always return to it, in whatever direction you may throw them away, and never rise upwards from the earth."[4][5]
In the 9th century, the eldest Banū Mūsā brother, Muhammad ibn Musa, in his Astral Motion and The Force of Attraction, hypothesized that there was a force of attraction between heavenly bodies,[6] foreshadowing Newton's law of universal gravitation.[7] In the 1000s, the Persian scientist Ibn al-Haytham (Alhacen), in the Mizan al-Hikmah, discussed the theory of attraction between masses, and it seems that he was aware of the magnitude of acceleration due to gravity.[8] In 1121, Al-Khazini, in The Book of the Balance of Wisdom, differentiated between force, mass, and weight,[9] and theorized that gravity varies with the distance from the centre of the Earth,[10] though he believed that the weight of heavy bodies increase as they are farther from the centre of the Earth.[11] All these early attempts at trying to explain the force of gravity were philosophical in nature.
Scientific revolution
Modern work on gravitational theory began with the work of Galileo Galilei in the late 16th century and early 17th century. In his famous (though probably apocryphal)[12] experiment dropping balls from the Tower of Pisa, and later with careful measurements of balls rolling down inclines, Galileo showed that gravitation accelerates all objects at the same rate. This was a major departure from Aristotle's belief that heavier objects are accelerated faster. [13] (Galileo correctly postulated air resistance as the reason that lighter objects may fall more slowly in an atmosphere.) Galileo's work set the stage for the formulation of Newton's theory of gravity.
Newton's theory of gravitation
In 1687, English mathematician Sir Isaac Newton published Principia, which hypothesizes the inverse-square law of universal gravitation. In his own words, “I deduced that the forces which keep the planets in their orbs must be reciprocally as the squares of their distances from the centers about which they revolve; and thereby compared the force requisite to keep the Moon in her orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly.” Forty-two years earlier Ismaël Bullialdus had proposed much the same theory.
Newton's theory enjoyed its greatest success when it was used to predict the existence of Neptune based on motions of Uranus that could not be accounted by the actions of the other planets. Calculations by John Couch Adams and Urbain Le Verrier both predicted the general position of the planet, and Le Verrier's calculations are what led Johann Gottfried Galle to the discovery of Neptune.
Ironically, it was another discrepancy in a planet's orbit that helped to point out flaws in Newton's theory. By the end of the 19th century, it was known that the orbit of Mercury showed slight perturbations that could not be accounted for entirely under Newton's theory, but all searches for another perturbing body (such as a planet orbiting the Sun even closer than Mercury) had been fruitless. The issue was resolved in 1915 by Albert Einstein's new General Theory of Relativity, which accounted for the small discrepancy in Mercury's orbit.
Although Newton's theory has been superseded, most modern non-relativistic gravitational calculations are still made using Newton's theory because it is a much simpler theory to work with than General Relativity, and gives sufficiently accurate results for most applications.
General relativity
In general relativity, the effects of gravitation are ascribed to spacetime curvature instead of a force. The starting point for general relativity is the equivalence principle, which equates free fall with inertial motion. The issue that this creates is that free-falling objects can accelerate with respect to each other. In Newtonian physics, no such acceleration can occur unless at least one of the objects is being operated on by a force (and therefore is not moving inertially).
To deal with this difficulty, Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. (This type of path is called a geodesic.) More specifically, Einstein discovered the field equations of general relativity, which relate the presence of matter and the curvature of spacetime and are named after him. The Einstein field equations are a set of 10 simultaneous, non-linear, differential equations. The solutions of the field equations are the components of the metric tensor of spacetime. A metric tensor describes a geometry of spacetime. The geodesic paths for a spacetime are calculated from the metric tensor.
Notable solutions of the Einstein field equations include:
- The Schwarzschild solution, which describes spacetime surrounding a spherically symmetric non-rotating uncharged massive object. For compact enough objects, this solution generated a black hole with a central singularity. For radial distances from the center which are much greater than the Schwarzschild radius, the accelerations predicted by the Schwarzschild solution are practically identical to those predicted by Newton's theory of gravity.
- The Reissner-Nordström solution, in which the central object has an electrical charge. For charges with a geometrized length which are less than the geometrized length of the mass of the object, this solution produces black holes with two event horizons.
- The Kerr solution for rotating massive objects. This solution also produces black holes with multiple event horizons.
- The Kerr-Newman solution for charged, rotating massive objects. This solution also produces black holes with multiple event horizons.
- The cosmological Robertson-Walker solution, which predicts the expansion of the universe.
General relativity has enjoyed much success because of how its predictions of phenomena which are not called for by the theory of gravity have been regularly confirmed. For example:
- General relativity accounts for the anomalous perihelion precession of Mercury.Template:Fn
- The prediction that time runs slower at lower potentials has been confirmed by the Pound-Rebka experiment, the Hafele-Keating experiment, and the GPS.
- The prediction of the deflection of light was first confirmed by Arthur Eddington in 1919, and has more recently been strongly confirmed through the use of a quasar which passes behind the Sun as seen from the Earth. See also gravitational lensing.
- The time delay of light passing close to a massive object was first identified by Irwin Shapiro in 1964 in interplanetary spacecraft signals.
- Gravitational radiation has been indirectly confirmed through studies of binary pulsars.
- The expansion of the universe (predicted by Alexander Friedmann) was confirmed by Edwin Hubble in 1929.
Gravity and quantum mechanics
Several decades after the discovery of general relativity it was realized that general relativity is incompatible with quantum mechanics.[14] It is possible to describe gravity in the framework of quantum field theory like the other fundamental forces, such that the attractive force of gravity arises due to exchange of virtual gravitons, in the same way as the electromagnetic force arises from exchange of virtual photons.[15][16] This reproduces general relativity in the classical limit. However, this approach fails at short distances of the order of the Planck length,[17] where a more complete theory of quantum gravity (or a new approach to quantum mechanics) is required. Many believe the complete theory to be string theory,[18] or more currently M Theory.
Specifics
Earth's gravity
Every planetary body (including the Earth) is surrounded by its own gravitational field, which exerts an attractive force on all objects. Assuming a spherically symmetrical planet (a reasonable approximation), the strength of this field at any given point is proportional to the planetary body's mass and inversely proportional to the square of the distance from the center of the body.
The strength of the gravitational field is numerically equal to the acceleration of objects under its influence, and its value at the Earth's surface, denoted g, is approximately expressed below as the standard average.
g = 9.8 m/s2 = 32.2 ft/s2
This means that, ignoring air resistance, an object falling freely near the earth's surface increases its velocity with 9.8 m/s (32.2 ft/s or 22 mph) for each second of its descent. Thus, an object starting from rest will attain a velocity of 9.8 m/s (32.2 ft/s) after one second, 19.6 m/s (64.4 ft/s) after two seconds, and so on, adding 9.8 m/s (32.2 ft/s) to each resulting velocity.
According to Newton's 3rd Law, the Earth itself experiences an equal and opposite force to that acting on the falling object, meaning that the Earth also accelerates towards the object. However, because the mass of the Earth is huge, the acceleration of the Earth by this same force is negligible, when measured relative to the system's center of mass.
Equations for a falling body near the surface of the Earth

Under an assumption of constant gravity, Newton’s law of gravitation simplifies to F = mg, where m is the mass of the body and g is a constant vector with an average magnitude of 9.81 m/s². The acceleration due to gravity is equal to this g. An initially-stationary object which is allowed to fall freely under gravity drops a distance which is proportional to the square of the elapsed time. The image on the right, spanning half a second, was captured with a stroboscopic flash at 20 flashes per second. During the first 1/20th of a second the ball drops one unit of distance (here, a unit is about 12 mm); by 2/20ths it has dropped at total of 4 units; by 3/20ths, 9 units and so on.
Under the same constant gravity assumptions, the potential energy, Ep, of a body at height h is given by Ep = mgh (or Ep = Wh, with W meaning weight). This expression is valid only over small distances h from the surface of the Earth. Similarly, the expression for the maximum height reached by a vertically projected body with velocity v is useful for small heights and small initial velocities only. In case of large initial velocities we have to use the principle of conservation of energy to find the maximum height reached. This same expression can be solved for v to determine the velocity of an object dropped from a height h immediately before hitting the ground, , assuming negligible air resistance.
Gravity and astronomy
The discovery and application of Newton's law of gravity accounts for the detailed information we have about the planets in our solar system, the mass of the Sun, the distance to stars, quasars and even the theory of dark matter. Although we have not traveled to all the planets nor to the Sun, we know their masses. These masses are obtained by applying the laws of gravity to the measured characteristics of the orbit. In space an object maintains its orbit because of the force of gravity acting upon it. Planets orbit stars, stars orbit galactic centers, galaxies orbit a center of mass in clusters, and clusters orbit in superclusters. The force of gravity is proportional to the mass of an object and inversely proportional to the square of the distance between the objects.
Gravitational radiation
In general relativity, gravitational radiation is generated in situations where the curvature of spacetime is oscillating, such as is the case with co-orbiting objects. The gravitational radiation emitted by the solar system is far too small to measure. However, gravitational radiation has been indirectly observed as an energy loss over time in binary pulsar systems such as PSR 1913+16. It is believed that neutron star mergers and black hole formation may create detectable amounts of gravitational radiation. Gravitational radiation observatories such as LIGO have been created to study the problem. No confirmed detections have been made of this hypothetical radiation, but as the science behind LIGO is refined and as the instruments themselves are endowed with greater sensitivity over the next decade, this may change.
Anomalies and discrepancies
There are some observations that are not adequately accounted for, which may point to the need for better theories of gravity or perhaps be explained in other ways.
- Stars on the outskirts of galaxies are moving faster than they should. Also galaxies within galaxy clusters are moving faster than they should. Dark Matter and MOND have both been proposed as explanations.
- The expansion of the universe seems to be speeding up. Dark Energy has been proposed to explain this. A recent alternative explanation is that the geometry of space is not homogeneous (due to clusters of galaxies) and that when the data is reinterpreted to take this into account, the expansion is not speeding up after all.[19]
- The Pioneer spacecraft seems to be slowing down in a way which has yet to be explained. [20]
- Various spacecraft have experienced greater accelerations during slingshot maneuvers than expected.
- An apparent frame dragging effect has been measured by Martin Tajmar and others which exceeds that predicted by General Relativity by many orders of magnitude.
Alternative theories
Historical alternative theories
- Aristotelian theory of gravity
- Le Sage's theory of gravitation (1784) also called LeSage gravity, proposed by Georges-Louis Le Sage, based on a fluid-based explanation where a light gas fills the entire universe.
- Nordström's theory of gravitation (1912, 1913), an early competitor of general relativity.
- Whitehead's theory of gravitation (1922), another early competitor of general relativity.
Recent alternative theories
- Brans-Dicke theory of gravity (1961)
- Induced gravity (1967), a proposal by Andrei Sakharov according to which general relativity might arise from quantum field theories of matter
- Rosen bi-metric theory of gravity
- In the modified Newtonian dynamics (MOND) (1981), Mordehai Milgrom proposes a modification of Newton's Second Law of motion for small accelerations
- The new and highly controversial Process Physics theory attempts to address gravity
- The self-creation cosmology theory of gravity (1982) by G.A. Barber in which the Brans-Dicke theory is modified to allow mass creation
- Nonsymmetric gravitational theory (NGT) (1994) by John Moffat
- Tensor-vector-scalar gravity (TeVeS) (2004), a relativistic modification of MOND by Jacob Bekenstein
- Process physics, an information-theoretical non-geometric modelling of reality.
See also
- Anti-gravity, the idea of neutralizing or repelling gravity
- Artificial gravity
- Escape velocity, the minimum velocity needed to fly away from a massive space object
- General relativity
- g-force, a measure of acceleration
- Gravitational field
- Gravitational waves
- Gravitational binding energy
- Gravity Research Foundation
- Gauss's law for gravity
- Jovian-Plutonian gravitational effect
- Kepler's third law of planetary motion
- Newton's laws of motion
- n-body problem
- The Pioneer spacecraft anomaly
- Scalar Gravity
- Speed of gravity
- Standard gravitational parameter
- Standard gravity
- Weight
- Weightlessness
- Lagrange Points
- Gravity assist
Notes
- Template:Fnb Proposition 75, Theorem 35: p.956 - I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I. Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
- Template:Fnb Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)
Footnotes
- ^ Does Gravity Travel at the Speed of Light?, UCR Mathematics. 1998. Retrieved 3 July 2008
- ^ Dick Teresi (2002), Lost Discoveries: The Ancient Roots of Modern Science - from the Babylonians to the Maya, Simon & Schuster, New York, ISBN 0-684-83718-8:
"Two hundred years before Pythagoras, philosophers in northern India had understood that gravitation held the solar system together, and that therefore the sun, the most massive object, had to be at its centre."
- ^ S. Kak (2003). Indian Physics: Outline of Early History, p. 22. arXiv. Louisiana State University. [unreliable source?]
- ^ Brahmagupta (628 AD). Brahmasphuta Siddhanta ("The Opening of the Universe").
- ^ Al-Biruni (1030). Ta'rikh al-Hind (Indica).
- ^ K. A. Waheed (1978). Islam and The Origins of Modern Science, p. 27. Islamic Publication Ltd., Lahore.
- ^ Robert Briffault (1938). The Making of Humanity, p. 191.
- ^ Dr. Nader El-Bizri, "Ibn al-Haytham or Alhazen", in Josef W. Meri (2006), Medieval Islamic Civilization: An Encyclopaedia, Vol. II, p. 343-345, Routledge, New York, London.
- ^ Donald Routledge Hill (1993), Islamic Science and Engineering, p. 61, Edinburgh University Press. (cf. Salah Zaimeche PhD (2005), Merv, p. 5, Foundation for Science Technology and Civilization.)
- ^ Professor Mohammed Abattouy (2002). "The Arabic Science of weights: A Report on an Ongoing Research Project", The Bulletin of the Royal Institute for Inter-Faith Studies 4, p. 109-130.
- ^ N. Khanikoff, ed. and trans. (1858-1860), "Analysis and Extracts of ... Book of the Balance of Wisdom, An Arabic Work on the Water-Balance, Written by 'Al-Khâzinî in the Twelfth Century", chap. 5, sect. 3.1, Journal of the American Oriental Society 6, p. 36.
- ^ Ball, Phil (2005). "Tall Tales". Nature News. doi:10.1038/news050613-10. ISSN 0028-0836.
{{cite journal}}:|access-date=requires|url=(help); Unknown parameter|month=ignored (help) - ^ Galileo (1638), Two New Sciences, First Day Salviati speaks: "If this were what Aristotle meant you would burden him with another error which would amount to a falsehood; because, since there is no such sheer height available on earth, it is clear that Aristotle could not have made the experiment; yet he wishes to give us the impression of his having performed it when he speaks of such an effect as one which we see."
- ^ Randall, Lisa (2005). Warped Passages: Unraveling the Universe's Hidden Dimensions. Ecco. ISBN 0-06-053108-8.
- ^ Feynman, R. P. (1995). Feynman lectures on gravitation. Addison-Wesley. ISBN 0201627345.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Zee, A. (2003). Quantum Field Theory in a Nutshell. Princeton University Press. ISBN 0-691-01019-6.
- ^ Randall, Lisa (2005). Warped Passages: Unraveling the Universe's Hidden Dimensions. Ecco. ISBN 0-06-053108-8.
- ^ Greene, Brian (2000). The elegant universe: superstrings, hidden dimensions, and the quest for the ultimate theory. New York: Vintage Books. ISBN 0375708111.
- ^ [1] Dark energy may just be a cosmic illusion New Scientist
- ^ [2] Wanted: Einstein Jr, Mar 6th 2008 The Economist
References
- Halliday, David (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Serway, Raymond A. (2004). Physics for Scientists and Engineers (6th ed. ed.). Brooks/Cole. ISBN 0-534-40842-7.
{{cite book}}:|edition=has extra text (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed. ed.). W. H. Freeman. ISBN 0-7167-0809-4.
{{cite book}}:|edition=has extra text (help)
External links
- Chapter 10. Gravity, from Light and Matter: educational materials for physics and astronomy
- Gravity Probe B Experiment The Official Einstein website from Stanford University
- Center for Gravity, Electrical, and Magnetic Studies
- Gravity for kids (flash)
- Ask a scientist, Physics Archive
- How stuff works:
- Alternative theory of gravity explains large structure formation -- without dark matter PhysOrg.com
- Do it yourself, gravitation experiment
- How to calculate the size of the gravitation
- Gravity simulator - watch gravity in action


