Acid dissociation constant

The weak acid acetic acid donates a proton to water in an equilibrium reaction to give the acetate ion and the hydronium ion. Key: Hydrogen is white, oxygen is red, carbon is gray. Lines are chemical bonds.

An acid dissociation constant, K_a, (also known as acidity constant, or acid-ionization constant) is a quantitative measure of the strength of an acid in solution: the larger the value the stronger the acid and the more the acid is dissociated, at a given concentration, into its conjugate base and the hydrogen ion.

K_a is an equilibrium constant. For an equilibrium between a generic acid, HA, and its conjugate base, A⁻, HA $\rightleftharpoons$ A⁻ + H⁺, K_a is defined, subject to certain conditions, as

$K_{a}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}}$

where [HA], [A⁻] and [H⁺] are equilibrium concentrations of the reactants.

The term acid dissociation constant is also used for pK_a, which is equal to −log₁₀ K_a. As K_a increases pK_a decreases. In aqueous solution, acids that release a single proton are partially dissociated to an appreciable extent in the pH range pK_a ± 2. The actual extent of the dissociation can be calculated if the acid concentration and pH are known.

The term pK_b is used in relation to bases, though pK_b has faded from modern use due to the easy relationship available between pK_b and pK_a, the strength of its conjugate acid. Though discussions of this topic typically assume water as the solvent, particularly at introductory levels, the Brønsted–Lowry acid-base theory is versatile enough that acidic behavior can now be characterized even in non-aqueous solutions.

A knowledge of pK_a values is essential for the understanding of the behaviour of acids and bases in solution. For example, many compounds used for medication are weak acids or bases, so a knowledge of the pK_a and log p values is essential for an understanding of how the compound enters (or does not enter) the blood stream. Other applications include aquatic chemistry, chemical oceanography, buffer solutions, acid-base homeostasis and certain kinds of enzyme kinetics, such as Michaelis–Menten kinetics, which involve a pre-equilibrium step. Also, knowledge of pK_a values is a prerequisite for a quantitative understanding of the interaction between acids or bases and metal ions to form complexes in solution.

Acids and bases:

Acid dissociation constant
Acid-base extraction
Acid-base reaction
Acid-base catalysis
Acid-base physiology
Acid-base homeostasis
Acidity function
Buffer solution
Dissociation constant
Non-nucleophilic base
pH
Proton affinity
Self-ionization of water

  Lewis acid/base
  Mineral acid/base
  Organic acid/base
  Weak acid/base
  Strong acid/base
  Super acid/base

Definitions

According to Arrhenius's original definition, an acid is a substance which dissociates in aqueous solution, releasing the hydrogen ion.

HA $\rightleftharpoons$ A⁻ + H⁺

The equilibrium constant for this "dissociation" reaction is known as a dissociation constant. However, since the liberated proton combines with a water molecule to give a hydronium ion (also called oxonium), Arrhenius proposed that the "dissociation" reaction should be written as an acid-base reaction.

HA + H₂O $\rightleftharpoons$ A⁻ + H₃O⁺

Brønsted and Lowry generalized this definition as a proton exchange reaction, as follows.

acid + base $\rightleftharpoons$ conjugate base + conjugate acid

The acid donates a proton to the base. The conjugate base is what is left after the acid has lost a proton and the conjugate acid is created when the base gains a proton. For aqueous solutions an acid, HA, reacts with the base, water, donating a proton to it, creating the conjugate base, A⁻, and the conjugate acid, the hydronium ion. The Brønsted–Lowry definition is particularly useful when the solvent is a substance other than water, such as dimethyl sulfoxide; in that case the solvent, S, acts as a base, accepting a proton and forming the conjugate acid SH⁺. It also puts acids and bases on the same footing as being, respectively, donors or acceptors of protons. The conjugate acid, BH⁺, of a base, B, "dissociates" according to

BH⁺ + OH⁻ $\rightleftharpoons$ B + H₂O

which is the reverse of the equilibrium

H₂O (acid) + B (base) $\rightleftharpoons$ OH⁻ (conjugate base) + BH⁺ (conjugate acid)

Note that in this case the hydroxide ion is acting as the conjugate base of the acid water though it is normally considered to be a base in its own right; the designation of an acid or base as "conjugate" depends on context.

Examples:

H₂CO₃ + H₂O $\rightleftharpoons$ HCO₃⁻ + H₃O⁺

The bicarbonate ion is the conjugate base of carbonic acid.

HCO₃⁻ + OH⁻ $\rightleftharpoons$ CO₃²⁻ + H₂O

and the bicarbonate ion is also the conjugate acid of the base, the carbonate ion. In fact the bicarbonate ion is amphiprotic, that is, it behaves as a base in the first example, and as an acid in the second example. These reactions are important for acid-base homeostasis in the human body (see carbonic acid).

Any compound subject to an hydrolysis equilibrium can also be classed as a weak acid since, in hydrolysis, protons are produced by the splitting of water molecules. For example, the equilibrium

B(OH)₃ + 2 H₂O $\rightleftharpoons$ B(OH)₄^- + H₃O⁺

shows why boric acid behaves as a weak acid even though it is not, itself, a proton donor. In a similar way, metal ion hydrolysis causes ions such as [Al(H₂O)₆]³⁺ to behave as weak acids.

[Al(H₂O)₆]³⁺ +H₂O $\rightleftharpoons$ [Al(H₂O)₅(OH)]²⁺ + H₃O⁺

It is important to note that, in the context of solution chemistry, a "proton" is understood to mean a solvated hydrogen ion. In aqueous solution the "proton" is a solvated hydronium ion.

Equilibrium Constant

Main article: Equilibrium constant

An acid dissociation constant is a particular example of an equilibrium constant. For the specific equilibrium between a monoprotic acid, HA and its conjugate base A⁻, in water,

HA + H₂O $\rightleftharpoons$ A⁻ + H₃O⁺

the thermodynamic equilibrium constant, K^t can be defined by

$K^{\mbox{t}}=\mathrm {\frac {{\{A^{-}\}}{\{H_{3}O^{+}\}}}{{\{HA\}}{\{H_{2}O\}}}}$

where {A} is the activity of the chemical species A etc (activity is a dimensionless quantity). Activities of the products are placed in the numerator, activities of the reactants are placed in the denominator. See Chemical equilibrium for a derivation of this expression.

Variation of pKa of acetic acid with ionic strength

Since activity is the product of concentration and activity coefficient the definition could also be written as

$K^{\mbox{t}}=\mathrm {{\frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}}\times {\frac {\gamma _{A^{-}}\gamma _{H_{3}O^{+}}}{\gamma _{HA}\gamma _{H_{2}O}}}=\mathrm {\frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}} \times \Gamma }$

where [HA] represents the concentration of HA and Γ is a quotient of activity coefficients.

In order to avoid the complications involved in using activities, dissociation constants are determined, where possible, in a medium of high ionic strength, that is, under conditions in which Γ can be assumed to be always constant. For example, the medium might be a solution of 0.1 M sodium nitrate or 3 M potassium perchlorate. Furthermore, in all but the most concentrated solutions it can be assumed that the concentration of water, [H₂O], is constant, approximately 55 mol dm⁻³. On dividing K^t by the constant terms and writing [H⁺] for the concentration of the hydronium ion the expression

$K_{a}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}}$

is obtained. This is the definition in common use. pK_a is defined as −log₁₀ K_a. Note, however, that all published dissociation constant values refer to the specific ionic medium used in their determination and that different values are obtained with different conditions, as shown for acetic acid in the illustration above.

When operating under the assumption that Γ is constant, the equilibrium constant does not change upon the addition of other chemicals to the solution. This assumption holds true when the concentration of spectator ions is low relative to the concentrations of other ions in the system. This allows, for example, for the behaviour of various ions to be explored at various pH values without worry that the equilibrium constant will also change. By exploiting this property, it is possible to obtain very complicated buffer solutions composed of many protonations of the same anion. This is accomplished with the addition of a strong acid to a solution of the anion. The conjugate base of the strong acid will act as a spectator ion, and the weak-base anion will be free to react with the proton as the equilibrium constant dictates.

Variation of the % formation of a monoprotic acid, AH, and its conjugate base, A⁻, with the difference between the pH and the pK_a of the acid

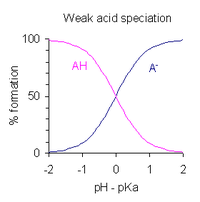
Monoprotic acids

After rearranging the expression defining K_a, and putting pH = −log₁₀[H⁺], one obtains

pH = pK_a – log ( [AH]/[A⁻] )

This is a form of the Henderson–Hasselbalch equation, from which the following conclusions can be drawn.

• At half-neutralization [AH]/[A⁻] = 1; since log(1) =0 , the pH at half-neutralization is numerically equal to pK_a.
• The buffer region extends over the approximate range pK_a ± 2, though buffering is weak outside the range pK_a ± 1. At pK_a ± 1 [AH]/[A⁻]=10 or 1/10.
• if the pH is known the ratio [AH]:[A⁻] may be calculated. This ratio is independent of the analytical concentration of the acid.

In water, measurable pK_a values range from about –2 for a strong acid to about 12 for a very weak acid (or strong base). All acids with a pK_a value of less than -2 are more than 99% dissociated at pH 0 (1M acid). This is known as solvent leveling: since all such acids are brought to the same level of being strong acids, regardless of their pK_a values. Likewise, all bases with a pK_a value larger than the upper limit are more than 99% de-protonated at all attainable pH values and are classified as strong bases.

An example of a strong acid is hydrochloric acid, HCl, which has a pK_a value, estimated from thermodynamic quantities, of –9.3 in water. The concentration of undissociated acid in a 1 mol dm^-3 solution, will be less than 10^-4 mol dm^-3. In common parlance the acid is said to be fully dissociated..

The extent of dissociation and pH of a solution of a monoprotic acid can be easily calculated when the pK_a and analytical concentration of the acid are known. See ICE table for details.

Polyprotic acids

 % species' formation as a function of pH

% species formation calculated with the program HySS for a 10mM solution of citric acid. pK_a1=3.13, pK_a2 = 4.76, pK_a3=6.40.

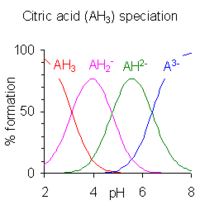
Polyprotic acids are acids which can lose more than one proton. The constant for dissociation of the first proton may be denoted as K_a1 and the constants for dissociation of successive protons as K_a2, etc.

When the difference between successive pK values is about four or more, each species may be considered as an acid in its own right; the pH range of existence of each species is about pK± 2, so there is very little overlap between the ranges for successive species. The case of phosphoric acid illustrates this point. In fact salts of either H₂PO₄⁻ or HPO₄²⁻ may be crystallized from solution by adjustment of pH to either 4 or 10.

When the difference between successive pK values is less than about four there is overlap between the pH range of existence of the species in equilibrium. The smaller the difference, the more the overlap. The case of citric acid is shown at the right; solutions of citric acid are buffered over the whole range of pH 2.5 to 7.5.

It is generally true that successive pK values increase (Pauling's first rule). For example, for a diprotic acid, H₂A, the two equilibria are

H₂A $\rightleftharpoons$ HA⁻ + H⁺

HA⁻ $\rightleftharpoons$ A²⁻ + H⁺

it can be seen that the second proton is removed from a negatively charged species. Since the proton carries a positive charge extra work is needed to remove it; that is the cause of the trend noted above. Phosphoric acid, H₃PO₄, (values below), illustrates this rule, as does vanadic acid. When an exception to the rule is found it indicates that a major change in structure is occurring. In the case of VO₂⁺_(aq), the vanadium is octahedral, 6-coordinate, whereas all the other species are tetrahedral, 4-coordinate. This explains why pK_a1 > pK_a2 for vanadium(V) oxoacids.

		VO2+$\rightleftharpoons$ H3VO4 + H+	pKa1 = 4.2
H3PO4 $\rightleftharpoons$ H2PO4− + H+	pKa1 = 2.15	H3VO4 $\rightleftharpoons$ H2VO4− + H+	pKa2 = 2.60
H2PO4− $\rightleftharpoons$ HPO42− + H+	pKa2 = 7.20	H2VO4− $\rightleftharpoons$ HVO42− + H+	pKa3 = 7.92
HPO42− $\rightleftharpoons$ PO43− + H+	pKa3 = 12.37	HVO42− $\rightleftharpoons$ VO43− + H+	pKa4 = 13.27

Water self-ionization

Main article: Self-ionization of water

Water has both acidic and basic properties. The equilibrium constant for the equilibrium

H₂O + H₂O $\rightleftharpoons$ OH⁻ + H₃O⁺

is given by

$K_{a}=\mathrm {\frac {[H^{+}][OH^{-}]}{[H_{2}O]^{2}}}$

When, as is usually the case, the concentration of water can be assumed to be constant, this expression simplifies to

$K_{w}=[H^{+}][OH^{-}]\,$

The self-ionization constant of water, K_w, can thus be seen as a special case of an acid dissociation constant.

Bases

Main article: Base (chemistry)

Historically the equilibrium constant K_b for a base was defined as the association constant for protonation of the base, B, to form the conjugate acid, HB⁺.

B + H₂O $\rightleftharpoons$ HB⁺ + OH⁻

Using similar reasoning to that used before

$K_{b}=\mathrm {\frac {[HB^{+}][OH^{-}]}{[B]}}$

In water, the concentration of the hydroxide ion, [OH⁻], is related to the concentration of the hydrogen ion by K_w = [H⁺][OH^–], therefore

$\mathrm {[OH^{-}]={\frac {{\mathit {K}}_{w}}{[H^{+}]}}}$

Substitution of the expression for [OH⁻] into the expression for K_b gives

$\mathrm {{\mathit {K}}_{b}={\frac {[HB^{+}]{\mathit {K}}_{w}}{[B][H^{+}]}}={\frac {{\mathit {K}}_{w}}{{\mathit {K}}_{a}}}}$

It follows, taking cologarithms, that pK_b = pK_w – pK_a. In aqueous solutions at 25 °C, pK_w is 13.9965, so pK_b ~ 14 – pK_a.

In effect there is no need to define pK_b separately from pK_a, but it is done here because pK_b values can be found in the older literature.

Temperature dependence

Main article: Van 't Hoff equation

All equilibrium constants vary with temperature according to the van 't Hoff equation

${\frac {\operatorname {d} \ln {\mathit {K}}}{\operatorname {d} T}}={\frac {{\Delta {\mathit {H}}_{m}}^{\ominus }}{RT^{2}}}$

Thus, for exothermic reactions, (ΔH^o is negative) K decreases with temperature, but for endothermic reactions (ΔH^o is positive) K increases with temperature.

Acidity in nonaqueous solutions

A solvent will be more likely to promote ionization of a dissolved acidic molecule if:

1. it is a protic solvent, capable of forming hydrogen bonds
2. it has a high donor number, making it a strong Lewis base.
3. it has a high dielectric constant (relative permittivity), making it a good solvent for ionic species.

Solvents can be polar, protic, donor or non-polar. The data in the following table refer to a temperature at or near 25 °C, unless stated otherwise.

Compound	Solvent Class	Dielectric constant
1,4-Dioxane	Non-polar, Donor	2.2
Hexane	Non-polar	1.9
Carbon tetrachloride	Non-polar	2.2
Benzene	Non-polar	2.3
Diethyl ether	Non-polar, Donor	4.3
Acetic acid	Protic donor	6.1
Tetrahydrofuran	Donor	7.6
Acetone	Polar donor	21
Liquid ammonia	Polar donor	25 at 195 K
Acetonitrile	Polar donor	37
Dimethylsulfoxide	Polar donor	47
Water	Polar protic donor	78
Formamide	Polar protic donor	111
Sulphuric acid	Polar protic	110

Ionization of acids is less in an acidic solvent than in water. For example, hydrogen chloride is a weak acid when dissolved in acetic acid. This is because acetic acid is a much weaker base than water.

HCl + CH₃CO₂H $\rightleftharpoons$ Cl⁻ + CH₃C(OH)₂⁺

acid + base $\rightleftharpoons$ conjugate base + conjugate acid

Compare this reaction with what happens when acetic acid is dissolved in the more acidic solvent pure sulphuric acid

H₂SO₄ + CH₃CO₂H $\rightleftharpoons$ HSO₄⁻ + CH₃C(OH)₂⁺

The apparently unlikely geminal diol species CH₃C(OH)₂⁺ is stable in these environments.

pK_a values of organic compounds are often obtained using solvents other than water, such as dimethyl sulfoxide (DMSO) and acetonitrile. Water is more basic than DMSO so most acids dissociate to a lesser extent in DMSO than in water. DMSO is widely used as an alternative to water in evaluating acids and bases because it has a lower dielectric constant than water, it is less polar and so dissolves non-polar, hydrophobic substances more easily.

Below is a table of selected pK_a values at 25 °C in acetonitrile (AN) and dimethyl sulfoxide (DMSO). Values for water are included for comparison.

HA $\rightleftharpoons$ A− + H+	AN	DMSO	water
p-Toluenesulfonic acid	8.5	0.9	strong
2,4-Dinitrophenol	16.66	5.1	3.9
Benzoic acid	21.51	11.1	4.2
Acetic acid	23.51	12.6	4.756
Phenol	29.14	18.0	9.99

BH+ $\rightleftharpoons$ B + H+	AN	DMSO	water
Pyrrolidine	19.56	10.8	11.4
Triethylamine	18.82	9.0	10.72
Proton sponge	18.62	7.5	12.1
Pyridine	12.53	3.4	5.2
Aniline	10.62	3.6	9.4

In solvents of low dielectric constant ions tend to associate forming ion pairs and clusters, which complicates the interpretation of pK_a values.

dimerization of a carboxylic acid

In aprotic solvents, oligomers may be formed by hydrogen bonding. An acid may also form hydrogen bonds to its conjugate base. This process is known as homoconjugation. Homoconjugation has the effect of enhancing the acidity of acids, lowering their effective pK_a values, by stabilizing the conjugate base. Due to homoconjugation, the proton-donating power of toluenesulfonic acid in acetonitrile solution is enhanced by a factor of nearly 800.

Homoconjugation does not occur in aqueous solutions because water forms stronger hydrogen bonds and prevents the oligomers from forming.

Mixed solvents

When a compound has limited solubility in water it is common practice (in the pharmaceutical industry, for example) to determine pK_a values in a solvent mixture such as water/dioxane or water/methanol, in which the compound is more soluble. However, a pK_a value obtained in a mixed solvent cannot be used directly for aqueous solutions. The reason for this is that when the solvent is in its standard state its activity is defined as one. For example, the standard state of water:dioxane 9:1 is precisely that solvent mixture, with no added solutes. To obtain the pK_a value for use with aqueous solutions it has to be extrapolated to zero co-solvent concentration from values obtained from various co-solvent mixtures.

These facts are obscured by the omission of the solvent from the expression which is normally used to define pK_a, but pK_a values obtained in a given mixed solvent can be compared to each other, giving relative acid strengths. The same is true of pK_a values obtained in a particular non-aqueous solvent such as DMSO.

A universal, solvent-independent, scale for acid dissociation constants has not yet been developed, since there is no known way to compare the standard states of two different solvents.

Factors that determine the relative strengths of acids

Pauling's second rule states that the value of the first pK_a for acids of the formula XO_m(OH) _n is approximately independent of n and X and is approximately 8 for m = 0, 2 for m = 1, −3 for m = 2 and < −10 for m = 3. This correlates with the oxidation state of the central atom, X: the higher the oxidation state the stronger the oxyacid. For example, pK_a for HClO is 7.2, for HClO₂ is 2.0, for HClO₃ is −1 and HClO₄ is a strong acid.

fumaric acid

maleic acid

With organic acids inductive effects and mesomeric effects affect the pK_a values. The effects are summarised in the Hammett equation and subsequent extensions.

Structural effects can also be important. The difference between fumaric acid and maleic acid is a classic example. Fumaric acid is (E)-1,4-but-2-enedioic acid, a trans isomer, whereas maleic acid is the corresponding cis isomer, i.e. (Z)-1,4-but-2-enedioic acid (see cis-trans isomerism). Fumaric acid has pK_a values of approximately 3.5 and 4.5. By contrast, maleic acid has pK_a values of approximately 1.5 and 6.5. The reason for this large difference is that when one proton is removed from the cis- isomer (maleic acid) a strong intramolecular hydrogen bond is formed with the nearby remaining carboxyl group. This favors the formation of the maleate H⁺, and it opposes the removal of the second proton from that species. In the trans isomer, the two carboxyl groups are always far apart, so hydrogen bonding is not observed.

proton sponge

Proton sponge, 1,8-Bis(dimethylamino)naphthalene, has a pK_a value of 12.1. It is one of the strongest amine bases known. The high basicity is attributed to the relief of strain upon protonation and strong internal hydrogen bonding.

Thermodynamics

An equilibrium constant is related to the standard Gibbs free energy change for the reaction, so for an acid dissociation constant

ΔG^θ = 2.303 RT pK_a.

Note that pK_a= –log K_a. At 25 °C ΔG^θ/kJ mol^-1 = 5.708 pK_a. Free energy is made up of an enthalpy term and an entropy term.

ΔG^θ = ΔH^θ – TΔS^θ

The standard enthalpy change can be determined by calorimetry or by using the van't Hoff equation, though the calorimetric method is preferable. When both the standard enthalpy change and acid dissociation constant have been determined, the standard entropy change is easily calculated from the equation above. In the following table, the entropy terms are calculated from the experimental values of pK_a and ΔH^θ. The data were critically selected and refer to 25 °C and zero ionic strength, in water.

Acids

Compound	Equilibrium	pKa	ΔHθ /kJ mol−1	–TΔSθ /kJ mol−1
HA = Acetic acid	HA $\rightleftharpoons$ H+ + A−	4.756	−0.41	27.56
H2A+ = GlycineH+	H2A+ $\rightleftharpoons$ HA + H+	2.351	4.00	9.419
	HA $\rightleftharpoons$ H+ + A−	9.78	44.20	11.6
H2A = Maleic acid	H2A $\rightleftharpoons$ HA− + H+	1.92	1.10	9.85
	HA− $\rightleftharpoons$ H+ + A2−	6.27	−3.60	39.4
H3A = Citric acid	H3A $\rightleftharpoons$ H2A− + H+	3.128	4.07	13.78
	H2A− $\rightleftharpoons$ HA2− + H+	4.76	2.23	24.9
	HA2− $\rightleftharpoons$ A3− + H+	6.40	−3.38	39.9
HA = Boric acid	HA $\rightleftharpoons$ H+ + A−	9.237	13.80	38.92
H3A = Phosphoric acid	H3A $\rightleftharpoons$ H2A− + H+	2.148	−8.00	20.26
	H2A− $\rightleftharpoons$ HA2− + H+	7.20	3.60	37.5
	HA2− $\rightleftharpoons$ A3− + H+	12.35	16.00	54.49
HA− = Hydrogen sulphate	HA− $\rightleftharpoons$ A2− + H+	1.99	−22.40	33.74
H2A = Oxalic acid	H2A $\rightleftharpoons$ HA− + H+	1.27	−3.90	11.15
	HA− $\rightleftharpoons$ A2− + H+	4.266	7.00	31.35

Conjugate acid of bases

Compound	Equilibrium	pKa	ΔHθ /kJ mol−1	–TΔSθ /kJ mol−1
B = Ammonia	HB+ $\rightleftharpoons$ B + H+	9.245	51.95	0.8205
B = Methylamine	HB+ $\rightleftharpoons$ B + H+	10.645	55.34	5.422
B = Triethylamine	HB+ $\rightleftharpoons$ B + H+	10.72	43.13	18.06

The first point to note is that when pK_a is positive, the standard free energy change for the dissociation reaction is also positive, that is, dissociation of a weak acid is not a spontaneous process. Secondly some reactions are exothermic and some are endothermic, but when ΔH^θ is negative –TΔS^θ is the dominant factor which determines that ΔG^θ is positive. Lastly, the entropy contribution is always unfavourable in these reactions.

Note that the standard free energy change for the reaction is for the changes from the reactants in their standard states to the products in their standard states. The free energy change at equilibrium is zero, by definition, since the chemical potentials of reactants and products are equal at equilibrium.

Experimental determination of pK_a values

Main article: Determination of equilibrium constants

A calculated titration curve of oxalic acid titrated with a solution of sodium hydroxide

pK_a values are commonly determined by means of titrations, in a medium of high ionic strength and at constant temperature. A typical procedure would be as follows. A solution of the compound in the medium is acidified with a strong acid to the point where the compound is fully protonated. The solution is then titrated with a strong base until all the protons have been removed. At each point in the titration pH is measured using a pH meter. The equilibrium constants are found by fitting calculated pH values to the observed values, using the method of least squares.

The total volume of added strong base should be small compared to the initial volume of to keep the ionic strength nearly constant. This will ensure that pK_a remains invariant during the titration.

A calculated titration curve for oxalic acid is shown at the right. Oxalic acid has pK_a values of 1.27 and 4.27. Therefore the buffer regions will be centered at about pH 1.3 and pH 4.3. The buffer regions carry the information necessary to get the pK_a values as the concentrations of acid and conjugate base change along a buffer region.

Between the two buffer regions there is an end-point, or equivalence point, where the pH rises by about two units. This end-point is not sharp and is typical of a diprotic acid whose buffer regions overlap by a small amount: pK_a2 – pK_a1 is about three in this example. (If the difference in pK values were about two or less, the end-point would not be noticeable.) The second end-point begins at about pH 6.3 and is sharp. This indicates that all the protons have been removed. When this is so, the solution is not buffered and the pH rises steeply on addition of a small amount of strong base. However, the pH does not continue to rise indefinitely. A new buffer region begins at about pH 11 (pK_w – 3), which is where self-ionization of water becomes important.

It is very difficult to measure pH values of less than two with a glass electrode, because the Nernst equation breaks down at such low pH values. To determine pK values of less than about 2 or more than about 11 spectrophotometric or NMR measurements may be used instead of, or combined with, pH measurements.

Importance of pK_a values

A knowledge of pK_a values is important for the quantitative treatment of systems involving acid-base equilibria in solution. Applications include:

• Biochemistry
  Further information: [[:Protein pKa calculations]]

In biochemistry the pK_a values of proteins and amino acid side chains are of major importance for the activity of enzymes and the stability of proteins. The reaction that converts adenosine triphosphate to adenosine diphosphate is very pH sensistive.

• Buffer solutions
  Main article: buffer solutions

A buffer solution is made up of a mixture of an acid and its conjugate base, or a base and its conjugate acid. Compared with an aqueous solution, the pH of a buffer solution is relatively insensitive to the addition of a small amount of strong acid or strong base. The buffer capacity of a simple buffer solution (illustrative diagram) is largest when pH = pK_a.

Buffer solutions are used extensively in biochemistry to provide solutions at or near the physiological pH for the study of biochemical reactions. For example, MOPS provides a solution with pH 7.2. Buffers such as tricine are used in Gel electrophoresis. Isoelectric focussing is a technique used for separation of proteins by 2-D gel polyacrylamide gel electrophoresis. Buffering is essential in Acid base physiology including Acid-base homeostasis and disorders such as Acid-base imbalance.

• Coordination compounds
  Main article: Complex (chemistry)

A coordination complex is formed by interaction of a metal ion, M^m+, acting as a Lewis acid, with a ligand, L, acting as a Lewis base. However, the ligand may also undergo protonation reactions, so the formation of a complex in aqueous solution could be represented, symbolically by the reaction

[M(H₂O)_n]^m+ +LH $\rightleftharpoons$ [M(H₂O)_n−1L]^(m−1)+ + H₃O⁺

To determine the equilibrium constant for this reaction, in which the ligand loses a proton, the pK_a of the protonated ligand must be known. In practice, the ligand may be polyprotic; for example EDTA⁴⁻ can accept four protons; in that case, all pK_a values must be known. In addition, the metal ion is subject to hydrolysis, that is, it behaves as a weak acid, so the pK values for the hydrolysis reactions must also be known.

• Hazard assessment
  Main article: risk assessment

Knowledge of pK_a may be very important in assessing the hazard assciated with an acid or base. For example, hydrogen cyanide is a very toxic gas, because the cyanide ion inhibits the iron-containing enzyme cytochrome c oxidase. Hydrogen cyanide is a weak acid in aqueous solution with a pK_a of about 9. In strongly alkaline solutions, above pH 11, say, it follows that sodium cyanide is "fully dissociated" so the hazard due to the hydrogen cyanide gas is much reduced. An acidic solution, on the other hand, is very hazardous because all the cyanide is in its acid form. Ingestion of cyanide by mouth is potentially fatal, independently of pH, because of the reaction with cytochrome c oxidase.

• Natural waters

Acid-base equilibria are important for rivers and lakes, and in chemical oceanography.

• Pharmacology

Ionization of a compound alters its physical behavior and macro properties such as solubility and lipophilicity (log p). For example ionization of any compound will increase the solubility in water, but decrease the lipophilicity. This is exploited in drug development to increase the concentration of a compound in the blood by adjusting the pK_a of an ionizable group.

• pH indicators
  Main article: pH indicator

The transition range of a pH indicator is about pK_a ± 1. This is the range over which the color is intermediate between the colors of the acidic and basic forms of the indicator. A universal indicator is a mixture of indicators whose adjacent pK_a values differ by about two.

• Solvent extraction
  Main article: Acid-base extraction

In solvent extraction, the efficiency of extraction of a compound into an organic phase, such as ether, can be optimized by adjusting the pH of the aqueous phase using an appropriate buffer. At the optimum pH, the concentration of the electrically neutral species is maximized; such a species is more soluble in organic solvents having a low dielectric constant than it is in water. This technique is used for the purification of weak acids and bases.

pK_a of some common substances

There are multiple techniques to determine the pK_a of a chemical, leading to some discrepancies between different sources. Well measured values are typically within 0.1 units of each other. Data presented here was taken at 25 °C in water. More values can be found in thermodynamics, above.

Chemical Name	Equilibrium	pKa
B = Adenine	BH22+ $\rightleftharpoons$ BH+ + H+	4.17
	BH+ $\rightleftharpoons$ B + H+	9.65
H3A = Arsenic acid	H3A $\rightleftharpoons$ H2A− + H+	2.22
	H2A− $\rightleftharpoons$ HA2− + H+	6.98
	HA2− $\rightleftharpoons$ A3− + H+	11.53
HA = Benzoic acid	HA $\rightleftharpoons$ H+ + A−	4.204
HA = Butanoic acid	HA $\rightleftharpoons$ H+ + A−	4.82
H2A = Chromic acid	H2A $\rightleftharpoons$ HA− + H+	0.98
	HA− $\rightleftharpoons$ A2− + H+	6.5
B = Codeine	BH+ $\rightleftharpoons$ B + H+	8.17
HA = Cresol	HA $\rightleftharpoons$ H+ + A−	10.29
HA = Formic acid	HA $\rightleftharpoons$ H+ + A−	3.751
HA = Hydrofluoric acid	HA $\rightleftharpoons$ H+ + A−	3.17
HA = Hydrocyanic acid	HA $\rightleftharpoons$ H+ + A−	9.21
HA = Hydrogen selenide	HA $\rightleftharpoons$ H+ + A−	3.89
HA = Hydrogen peroxide (90%)	HA $\rightleftharpoons$ H+ + A−	11.7
HA = Lactic acid	HA $\rightleftharpoons$ H+ + A−	3.86
HA = Propanoic acid	HA $\rightleftharpoons$ H+ + A−	4.87
HA = Phenol	HA $\rightleftharpoons$ H+ + A−	9.99
H2A = L-(+)-Ascorbic Acid	H2A $\rightleftharpoons$ HA− + H+	4.17
	HA− $\rightleftharpoons$ A2− + H+	11.57

See also

• Determination of equilibrium constants
• Dissociation constant
• Henderson–Hasselbalch equation
• Hammett equation
• Isoelectric point
• Hydrolysis of metal salts
• QSAR

Further reading

• Atkins, P.W. (2008). Chemical Principles: The Quest for Insight (4th. edition ed.). W.H. Freeman. ISBN 1-4292-0965-8. {{cite book}}: |edition= has extra text (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Housecroft, C.E. (2008). Inorganic chemistry (3rd. ed. ed.). Prentice Hall. ISBN 0131755536. {{cite book}}: |edition= has extra text (help); Unknown parameter |coauthors= ignored (|author= suggested) (help) (Non-aqueous solvents)
• Hulanicki, A. (1987). Reactions of acids and bases in analytical chemistry. Horwood. ISBN 0853123306. (translation editor: Mary R. Masson)
• Leggett, D.J. (1985). Computational methods for the determination of formation constants. Plenum. ISBN 0306419572.
• Perrin, D. D. (1981). pKa prediction for organic acids and bases. Chapman and Hall. ISBN 041222190x. {{cite book}}: Check |isbn= value: invalid character (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Albert, A. (1971). The determination of ionization constants : a laboratory manual. Chapman and Hall. ISBN 0412103001. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help) (Previous edition published as Ionization constants of acids and bases. London: Methuen, 1962)

External links

• Acidity-Basicity Data (pKa Values) in Nonaqueous Solvents Extensive bibliography
• Shodor.org Acid-Base Chemistry
• Factors that Affect the Relative Strengths of Acids and Bases
• Purdue Chemistry
• Distribution diagrams of acids and bases (generation from pK_a values with free spreadsheet)
• SPARC Physical/Chemical property calculator
• List of Aqueous-Equilibrium Constants