Random walk
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (June 2009) |

A random walk is a mathematical formalization of a path that consists of a succession of random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the financial status of a gambler can all be modeled as random walks, although they may not be truly random in reality. The term random walk was first introduced by Karl Pearson in 1905.[1] Random walks have been used in many fields: ecology, economics, psychology, computer science, physics, chemistry, and biology.[2][3][4][5][6][7][8][9] Random walks explain the observed behaviors of processes in these fields, and thus serve as a fundamental model for the recorded stochastic activity.
Various different types of random walks are of interest. Often, random walks are assumed to be Markov chains or Markov processes, but other, more complicated walks are also of interest. Some random walks are on graphs, others on the line, in the plane, or in higher dimensions, while some random walks are on groups. Random walks also vary with regard to the time parameter. Often, the walk is in discrete time, and indexed by the natural numbers, as in . However, some walks take their steps at random times, and in that case the position is defined for the continuum of times . Specific cases or limits of random walks include the Lévy flight. Random walks are related to the diffusion models and are a fundamental topic in discussions of Markov processes. Several properties of random walks, including dispersal distributions, first-passage times and encounter rates, have been extensively studied.
Lattice random walk
This section needs additional citations for verification. (April 2011) |
A popular random walk model is that tollie of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. In a simple random walk, the location can only jump to neighboring sites of the lattice. In simple symmetric random walk on a locally finite lattice, the probabilities of the location jumping to each one of its immediate neighbours are the same. The best studied example is of random walk on the d-dimensional integer lattice (sometimes called the hypercubic lattice) .[citation needed]
One-dimensional random walk
An elementary example of a random walk is the random walk on the integer number line, , which starts at 0 and at each step moves +1 or −1 with equal probability.
This walk can be illustrated as follows. A marker is placed at zero on the number line and a fair coin is flipped. If it lands on heads, the marker is moved one unit to the right. If it lands on tails, the marker is moved one unit to the left. After five flips, it marker could now be on 1, −1, 3, −3, 5, or −5. With five flips, three heads and two tails, in any order, will land on 1. There are 10 ways of landing on 1 (by flipping three heads and two tails), 10 ways of landing on −1 (by flipping three tails and two heads), 5 ways of landing on 3 (by flipping four heads and one tail), 5 ways of landing on −3 (by flipping four tails and one head), 1 way of landing on 5 (by flipping five heads), and 1 way of landing on −5 (by flipping five tails). See the figure below for an illustration of the possible outcomes of 5 flips.

To define this walk formally, take independent random variables , where each variable is either 1 or −1, with a 50% probability for either value, and set and The series is called the simple random walk on . This series (the sum of the sequence of −1s and 1s) gives the distance walked, if each part of the walk is of length one. The expectation of is zero. That is, the mean of all coin flips approaches zero as the number of flips increase. This follows by the finite additivity property of expectation:
A similar calculation, using the independence of the random variables and the fact that , shows that:
This hints that , the expected translation distance after n steps, should be of the order of . In fact,
Derivation of dispersion proportionality If we have the situation where the probabilities of moving either left or right are equal, and , the probability of taking steps to the right out of a total of steps is given by since there are possible ways of taking and steps to the right and left, respectively. The probability of taking any of these independent steps is 1/2, and so we have the product . Now, the expectation value of taking steps is
It is generally the case that . Note the identity we have used with the binomial coefficient . We use it again below. We must then calculate the expectation value of :
It is generally the case that . The dispersion is
This result shows that diffusion is ineffective for mixing because of the way the square root behaves for large .
How many times will a random walk cross a boundary line if permitted to continue walking forever? A simple random walk on will cross every point an infinite number of times. This result has many names: the level-crossing phenomenon, recurrence or the gambler's ruin. The reason for the last name is as follows: a gambler with a finite amount of money will always lose when playing a fair game against a bank with an infinite amount of money. The gambler's money will perform a random walk, and it will reach zero at some point, and the game will be over.
If a and b are positive integers, then the expected number of steps until a one-dimensional simple random walk starting at 0 first hits b or −a is ab. The probability that this walk will hit b before −a is , which can be derived from the fact that simple random walk is a martingale.
Some of the results mentioned above can be derived from properties of Pascal's triangle. The number of different walks of n steps where each step is +1 or −1 is clearly 2n. For the simple random walk, each of these walks are equally likely. In order for Sn to be equal to a number k it is necessary and sufficient that the number of +1 in the walk exceeds those of −1 by k. Thus, the number of walks which satisfy is precisely the number of ways of choosing (n + k)/2 elements from an n element set (for this to be non-zero, it is necessary that n + k be an even number), which is an entry in Pascal's triangle denoted by . Therefore, the probability that is equal to . By representing entries of Pascal's triangle in terms of factorials and using Stirling's formula, one can obtain good estimates for these probabilities for large values of .
If the space is confined to + for brevity, the number of ways in which a random walk will land on any given number having five flips can be shown as {0,5,0,4,0,1}.
This relation with Pascal's triangle is demonstrated for small values of n. At zero turns, the only possibility will be to remain at zero. However, at one turn, there is one chance of landing on −1 or one chance of landing on 1. At two turns, a marker at 1 could move to 2 or back to zero. A marker at −1, could move to −2 or back to zero. Therefore, there is one chance of landing on −2, two chances of landing on zero, and one chance of landing on 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
The central limit theorem and the law of the iterated logarithm describe important aspects of the behavior of simple random walk on . In particular, the former entails that as n increases, the probabilities (proportional to the numbers in each row) approach a normal distribution.
As a Markov chain
A one-dimensional random walk can also be looked at as a Markov chain whose state space is given by the integers For some number p satisfying , the transition probabilities (the probability Pi,j of moving from state i to state j) are given by
Gaussian random walk
A random walk having a step size that varies according to a normal distribution is used as a model for real-world time series data such as financial markets. The Black–Scholes formula for modeling option prices, for example, uses a Gaussian random walk as an underlying assumption.
Here, the step size is the inverse cumulative normal distribution where 0 ≤ z ≤ 1 is a uniformly distributed random number, and μ and σ are the mean and standard deviations of the normal distribution, respectively.
If μ is nonzero, the random walk will vary about a linear trend. If vs is the starting value of the random walk, the expected value after n steps will be vs + nμ.
For the special case where μ is equal to zero, after n steps, the translation distance's probability distribution is given by N(0, nσ2), where N() is the notation for the normal distribution, n is the number of steps, and σ is from the inverse cumulative normal distribution as given above.
Proof: The Gaussian random walk can be thought of as the sum of a series of independent and identically distributed random variables, Xi from the inverse cumulative normal distribution with mean equal zero and σ of the original inverse cumulative normal distribution:
- Z = ,
but we have the distribution for the sum of two independent normally distributed random variables, Z = X + Y, is given by
- N(μX + μY, σ2X + σ2Y) (see here).
In our case, μX = μY = 0 and σ2X = σ2Y = σ2 yield
- N(0, 2σ2)
By induction, for n steps we have
- Z ~ N(0, nσ2).
For steps distributed according to any distribution with zero mean and a finite variance (not necessarily just a normal distribution), the root mean square translation distance after n steps is
But for the Gaussian random walk, this is just the standard deviation of the translation distance's distribution after n steps. Hence, if μ is equal to zero, and since the root mean square(rms) translation distance is one standard deviation, there is 68.27% probability that the rms translation distance after n steps will fall between ± σ. Likewise, there is 50% probability that the translation distance after n steps will fall between ± 0.6745σ.
Higher dimensions



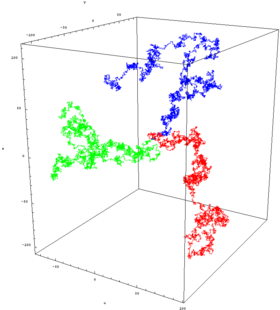
Imagine now a drunkard walking randomly in an idealized city. The city is effectively infinite and arranged in a square grid, and at every intersection, the drunkard chooses one of the four possible routes (including the one he came from) with equal probability. Formally, this is a random walk on the set of all points in the plane with integer coordinates. Will the drunkard ever get back to his home from the bar? It turns out that he will. This is the high dimensional equivalent of the level crossing problem discussed above. The probability of returning to the origin decreases as the number of dimensions increases. In three dimensions, the probability decreases to roughly 34%. A derivation, along with values of p(d) are discussed here: Pólya's Random Walk Constants.
The trajectory of a random walk is the collection of sites it visited, considered as a set with disregard to when the walk arrived at the point. In one dimension, the trajectory is simply all points between the minimum height the walk achieved and the maximum (both are, on average, on the order of √n). In higher dimensions the set has interesting geometric properties. In fact, one gets a discrete fractal, that is a set which exhibits stochastic self-similarity on large scales, but on small scales one can observe "jaggedness" resulting from the grid on which the walk is performed. The two books of Lawler referenced below are a good source on this topic.
Relation to Wiener process
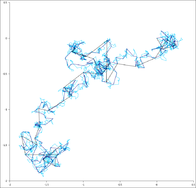
A Wiener process is a stochastic process with similar behaviour to Brownian motion, the physical phenomenon of a minute particle diffusing in a fluid. (Sometimes the Wiener process is called "Brownian motion", although this is strictly speaking a confusion of a model with the phenomenon being modeled.)
A Wiener process is the scaling limit of random walk in dimension 1.[citation needed] This means that if you take a random walk with very small steps you get an approximation to a Wiener process (and, less accurately, to Brownian motion). To be more precise, if the step size is ε, one needs to take a walk of length L/ε2 to approximate a Wiener process walk of length L. As the step size tends to 0 (and the number of steps increases proportionally) random walk converges to a Wiener process in an appropriate sense. Formally, if B is the space of all paths of length L with the maximum topology, and if M is the space of measure over B with the norm topology, then the convergence is in the space M. Similarly, a Wiener process in several dimensions is the scaling limit of random walk in the same number of dimensions.
A random walk is a discrete fractal (a function with integer dimensions; 1, 2, ...), but a Wiener process trajectory is a true fractal, and there is a connection between the two. For example, take a random walk until it hits a circle of radius r times the step length. The average number of steps it performs is r2.[citation needed] This fact is the discrete version of the fact that a Wiener process walk is a fractal of Hausdorff dimension 2.[citation needed]
In two dimensions, the average number of points the same random walk has on the boundary of its trajectory is r4/3. This corresponds to the fact that the boundary of the trajectory of a Wiener process is a fractal of dimension 4/3, a fact predicted by Mandelbrot using simulations but proved only in 2000 by Lawler, Schramm and Werner.[10]
A Wiener process enjoys many symmetries random walk does not. For example, a Wiener process walk is invariant to rotations, but random walk is not, since the underlying grid is not (random walk is invariant to rotations by 90 degrees, but Wiener processes are invariant to rotations by, for example, 17 degrees too). This means that in many cases, problems on random walk are easier to solve by translating them to a Wiener process, solving the problem there, and then translating back. On the other hand, some problems are easier to solve with random walks due to its discrete nature.
Random walk and Wiener process can be coupled, namely manifested on the same probability space in a dependent way that forces them to be quite close. The simplest such coupling is the Skorokhod embedding, but other, more precise couplings exist as well.
The convergence of a random walk toward the Wiener process is controlled by the central limit theorem. For a particle in a known fixed position at t = 0, the theorem tells us that after a large number of independent steps in the random walk, the walker's position is distributed according to a normal distribution of total variance:
where t is the time elapsed since the start of the random walk, is the size of a step of the random walk, and is the time elapsed between two successive steps.
This corresponds to the Green function of the diffusion equation that controls the Wiener process, which demonstrates that, after a large number of steps, the random walk converges toward a Wiener process.
In 3D, the variance corresponding to the Green's function of the diffusion equation is:
By equalizing this quantity with the variance associated to the position of the random walker, one obtains the equivalent diffusion coefficient to be considered for the asymptotic Wiener process toward which the random walk converges after a large number of steps:
- (valid only in 3D)
Remark: the two expressions of the variance above correspond to the distribution associated to the vector that links the two ends of the random walk, in 3D. The variance associated to each component , or is only one third of this value (still in 3D).
Anomalous diffusion
In disordered systems such as porous media and fractals may not be proportional to but to . The exponent is called the anomalous diffusion exponent and can be larger or smaller than 2.[11]
Applications
This section needs additional citations for verification. (February 2013) |

The following are some applications of random walk:
- In economics, the "random walk hypothesis" is used to model shares prices and other factors. Empirical studies found some deviations from this theoretical model, especially in short term and long term correlations. See share prices.
- In population genetics, random walk describes the statistical properties of genetic drift
- In physics, random walks are used as simplified models of physical Brownian motion and diffusion such as the random movement of molecules in liquids and gases. See for example diffusion-limited aggregation. Also in physics, random walks and some of the self interacting walks play a role in quantum field theory.
- In mathematical ecology, random walks are used to describe individual animal movements, to empirically support processes of biodiffusion, and occasionally to model population dynamics.
- In polymer physics, random walk describes an ideal chain. It is the simplest model to study polymers.
- In other fields of mathematics, random walk is used to calculate solutions to Laplace's equation, to estimate the harmonic measure, and for various constructions in analysis and combinatorics.
- In computer science, random walks are used to estimate the size of the Web. In the World Wide Web conference-2006, bar-yossef et al. published their findings and algorithms for the same.
- In image segmentation, random walks are used to determine the labels (i.e., "object" or "background") to associate with each pixel.[12] This algorithm is typically referred to as the random walker segmentation algorithm.
In all these cases, random walk is often substituted for Brownian motion.
- In brain research, random walks and reinforced random walks are used to model cascades of neuron firing in the brain.
- In vision science, fixational eye movements are well described by a random walk.[13]
- In psychology, random walks explain accurately the relation between the time needed to make a decision and the probability that a certain decision will be made.[14]
- Random walks can be used to sample from a state space which is unknown or very large, for example to pick a random page off the internet or, for research of working conditions, a random worker in a given country.[citation needed]
- When this last approach is used in computer science it is known as Markov Chain Monte Carlo or MCMC for short. Often, sampling from some complicated state space also allows one to get a probabilistic estimate of the space's size. The estimate of the permanent of a large matrix of zeros and ones was the first major problem tackled using this approach.[citation needed]
- Random walks have also been used to sample massive online graphs such as online social networks.
- In wireless networking, a random walk is used to model node movement.[citation needed]
- Motile bacteria engage in a biased random walk.[citation needed]
- Random walks are used to model gambling.[citation needed]
- In physics, random walks underlie the method of Fermi estimation.[citation needed]
Variants of random walks
A number of types of stochastic processes have been considered that are similar to the pure random walks but where the simple structure is allowed to be more generalized. The pure structure can be characterized by the steps being being defined by independent and identically distributed random variables.
Random walk on graphs
A random walk of length k on a possibly infinite graph G with a root 0 is a stochastic process with random variables such that and is a vertex chosen uniformly at random from the neighbors of . Then the number is the probability that a random walk of length k starting at v ends at w. In particular, if G is a graph with root 0, is the probability that a -step random walk returns to 0.
Assume now that our city is no longer a perfect square grid. When our drunkard reaches a certain junction he picks between the various available roads with equal probability. Thus, if the junction has seven exits the drunkard will go to each one with probability one seventh. This is a random walk on a graph. Will our drunkard reach his home? It turns out that under rather mild conditions, the answer is still yes. For example, if the lengths of all the blocks are between a and b (where a and b are any two finite positive numbers), then the drunkard will, almost surely, reach his home. Notice that we do not assume that the graph is planar, i.e. the city may contain tunnels and bridges. One way to prove this result is using the connection to electrical networks. Take a map of the city and place a one ohm resistor on every block. Now measure the "resistance between a point and infinity". In other words, choose some number R and take all the points in the electrical network with distance bigger than R from our point and wire them together. This is now a finite electrical network and we may measure the resistance from our point to the wired points. Take R to infinity. The limit is called the resistance between a point and infinity. It turns out that the following is true (an elementary proof can be found in the book by Doyle and Snell):
Theorem: a graph is transient if and only if the resistance between a point and infinity is finite. It is not important which point is chosen if the graph is connected.
In other words, in a transient system, one only needs to overcome a finite resistance to get to infinity from any point. In a recurrent system, the resistance from any point to infinity is infinite.
This characterization of recurrence and transience is very useful, and specifically it allows us to analyze the case of a city drawn in the plane with the distances bounded.
A random walk on a graph is a very special case of a Markov chain. Unlike a general Markov chain, random walk on a graph enjoys a property called time symmetry or reversibility. Roughly speaking, this property, also called the principle of detailed balance, means that the probabilities to traverse a given path in one direction or in the other have a very simple connection between them (if the graph is regular, they are just equal). This property has important consequences.
Starting in the 1980s, much research has gone into connecting properties of the graph to random walks. In addition to the electrical network connection described above, there are important connections to isoperimetric inequalities, see more here, functional inequalities such as Sobolev and Poincaré inequalities and properties of solutions of Laplace's equation. A significant portion of this research was focused on Cayley graphs of finitely generated groups. For example, the proof of Dave Bayer and Persi Diaconis that 7 riffle shuffles are enough to mix a pack of cards (see more details under shuffle) is in effect a result about random walk on the group Sn, and the proof uses the group structure in an essential way. In many cases these discrete results carry over to, or are derived from manifolds and Lie groups.
A good reference for random walk on graphs is the online book by Aldous and Fill. For groups see the book of Woess. If the transition kernel is itself random (based on an environment ) then the random walk is called a "random walk in random environment". When the law of the random walk includes the randomness of , the law is called the annealed law; on the other hand, if is seen as fixed, the law is called a quenched law. See the book of Hughes or the lecture notes of Zeitouni.
We can think about choosing every possible edge with the same probability as maximizing uncertainty (entropy) locally. We could also do it globally – in maximal entropy random walk (MERW) we want all paths to be equally probable, or in other words: for each two vertexes, each path of given length is equally probable. This random walk has much stronger localization properties.
Self-interacting random walks
There are a number of interesting models of random paths in which each step depends on the past in a complicated manner. All are more complex for solving analytically than the usual random walk; still, the behavior of any model of a random walker is obtainable using computers. Examples include:
- The self-avoiding walk (Madras and Slade 1996).[15]
The self-avoiding walk of length n on Z^d is the random n-step path which starts at the origin, makes transitions only between adjacent sites in Z^d, never revisits a site, and is chosen uniformly among all such paths. In two dimensions, due to self-trapping, a typical self-avoiding walk is very short,[16] while in higher dimension it grows beyond all bounds. This model has often been used in polymer physics (since the 1960s).
- The loop-erased random walk (Gregory Lawler).[17][18]
- The reinforced random walk (Robin Pemantle 2007).[19]
- The exploration process.[citation needed]
- The multiagent random walk.[20]
Long-range correlated walks
Long-range correlated time series are found in many biological, climatological and economic systems.
- Heartbeat records[21]
- Non-coding DNA sequences[22]
- Volatility time series of stocks[23]
- Temperature records around the globe[24]
Heterogeneous random walks in one dimension

Heterogeneous random walks in one dimension can have either discrete time or continuous time. The interval is also either discrete or continuous, and it is either finite or without bounds. In a discrete system, the connections are among adjacent states. The dynamics are either Markovian, Semi-Markovian, or even not-Markovian depending on the model. Heterogeneous random walks in 1D have jump probabilities that depend on the location in the system, and/or different jumping time (JT) probability density functions (PDFs) that depend on the location in the system.
Known important results in simple systems include:
- In a symmetric Markovian random walk, the Green's function (also termed the PDF of the walker) for occupying state i is a Gaussian in the position and has a variance that scales like the time. This result holds in a system with discrete time and space, yet also in a system with continuous time and space. This result is for systems without bounds.
- When there is a simple bias in the system (i.e. a constant force is applied on the system in a particular direction), the average distance of the random walker from its starting position is linear with time.
- When trying reaching a distance L from the starting position in a finite interval of length L with a constant force, the time for reaching this distance is exponential with the length L: , when moving against the force, and is linear with the length L: , when moving with the force. Without force: .
In a completely heterogeneous semi Markovian random walk in a discrete system of L (>1) states, the Green's function was found in Laplace space[25][26][27] (the Laplace transform of a function is defined with, ). Here, the system is defined through the jumping time (JT) PDFs: connecting state i with state j (the jump is from state i). The solution is based on the path representation of the Green's function, calculated when including all the path probability density functions of all lengths:
| (1) |
Here, and . Also, in Eq. (1),
| (2) |
and,
| (3) |
with,
| (4) |
and,
| (5) |
For L=1, . The symbol [L/2] that appears in the upper bound in the in eq. (3) is the floor operation (round towards zero). Finally, the factor in eq. (1) has the same form as in in eqs. (3)-(5), yet it is calculated on a lattice . Lattice is constructed from the original lattice by taking out from it the states i and j and the states between them, and then connecting the obtained two fragments. For cases in which a fragment is a single state, this fragment is excluded; namely, lattice is the longer fragment. When each fragment is a single state, .
Equations (1)-(5) hold for any 1D semi-Markovian random walk in a L-state chain, and form the most general solution in an explicit form for random walks in 1d.
See also
- Branching random walk
- Brownian motion
- Law of the iterated logarithm
- Lévy flight
- Lévy flight foraging hypothesis
- Loop-erased random walk
- Self avoiding walk
References
- ^ Pearson, K. (1905). The Problem of the Random Walk. Nature. 72, 294.
- ^ Van Kampen N. G., Stochastic Processes in Physics and Chemistry, revised and enlarged edition (North-Holland, Amsterdam) 1992.
- ^ Redner S., A Guide to First-Passage Process (Cambridge University Press, Cambridge, UK) 2001.
- ^ Goel N. W. and Richter-Dyn N., Stochastic Models in Biology (Academic Press, New York) 1974.
- ^ Doi M. and Edwards S. F., The Theory of Polymer Dynamics (Clarendon Press, Oxford) 1986
- ^ De Gennes P. G., Scaling Concepts in Polymer Physics (Cornell University Press, Ithaca and London) 1979.
- ^ Risken H., The Fokker–Planck Equation (Springer, Berlin) 1984.
- ^ Weiss G. H., Aspects and Applications of the Random Walk (North-Holland, Amsterdam) 1994.
- ^ Cox D. R., Renewal Theory (Methuen, London) 1962.
- ^ Dana Mackenzie, Taking the Measure of the Wildest Dance on Earth, Science, Vol. 290, no. 5498, pp. 1883–1884.
- ^ D. Ben-Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, 2000.
- ^ Leo Grady (2006): "Random Walks for Image Segmentation", IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 1768–1783, Vol. 28, No. 11
- ^ Ralf Engbert, Konstantin Mergenthaler, Petra Sinn, and Arkady Pikovsk: "An integrated model of fixational eye movements and microsaccades"
- ^ Nosofsky, 1997
- ^ Neal Madras and Gordon Slade (1996), The Self-Avoiding Walk, Birkhäuser Boston. ISBN 0-8176-3891-1.
- ^ S. Hemmer and P. C. Hemmer (1984), "An average self-avoiding random walk on the square lattice lasts 71 steps", J. Chem. Phys., 81: 584, Bibcode:1984JChPh..81..584H, doi:10.1063/1.447349
- ^ Gregory Lawler (1996). Intersection of random walks, Birkhäuser Boston. ISBN 0-8176-3892-X.
- ^ Gregory Lawler, Conformally Invariant Processes in the Plane, book.ps.
- ^ Robin Pemantle (2007), A survey of random processes with reinforcement.
- ^ Alamgir, M and von Luxburg, U (2010). "Multi-agent random walks for local clustering on graphs", IEEE 10th International Conference on Data Mining (ICDM), 2010, pp. 18-27.
- ^ C.-K. Peng, J. Mietus, J. M. Hausdorff, S. Havlin, H. E. Stanley, A. L. Goldberger (1993). "Long-range anticorrelations and non-gaussian behavior of the heartbeat". Phys. Rev. Lett. 70 (9): 1343–6. Bibcode:1993PhRvL..70.1343P. doi:10.1103/PhysRevLett.70.1343. PMID 10054352.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ C.-K. Peng, S. V. Buldyrev, A. L. Goldberger, S. Havlin, F. Sciortino, M. Simons, H. E. Stanley (1992). "Long-range correlations in nucleotide sequences". Nature. 356 (6365): 168–70. Bibcode:1992Natur.356..168P. doi:10.1038/356168a0. PMID 1301010.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Y. Liu, P. Cizeau, M. Meyer, C.-K. Peng, H. E. Stanley (1997). "Correlations in economic time series". Physica A. 245 (3–4): 437. doi:10.1016/S0378-4371(97)00368-3.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ E. Koscielny-Bunde, A. Bunde, S. Havlin, H. E. Roman, Y. Goldreich, H.-J. Schellenhuber (1998). "Indication of a universal persistence law governing atmospheric variability". Phys. Rev. Lett. 81 (3): 729. Bibcode:1998PhRvL..81..729K. doi:10.1103/PhysRevLett.81.729.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Flomenbom O. and Klafter J., Phys. Rev. Lett., 95 (2005) 098105-1
- ^ Flomenbom O. and Silbey R. J., J. Chem. Phys. 127, 034102 (2007).
- ^ Flomenbom O and Silbey RJ, Phys. Rev. E 76, 041101 (2007).
Bibliography
- David Aldous and Jim Fill, Reversible Markov Chains and Random Walks on Graphs, http://stat-www.berkeley.edu/users/aldous/RWG/book.html
- Doyle, Peter G.; Snell, J. Laurie (1984). Random walks and electric networks. Carus Mathematical Monographs. Vol. 22. Mathematical Association of America. arXiv:math.PR/0001057. ISBN 978-0-88385-024-4. MR 0920811Template:Inconsistent citations
{{cite book}}: CS1 maint: postscript (link) - William Feller (1968), An Introduction to Probability Theory and its Applications (Volume 1). ISBN 0-471-25708-7
- Chapter 3 of this book contains a thorough discussion of random walks, including advanced results, using only elementary tools.
- Barry D. Hughes (1996), Random walks and random environments, Oxford University Press. ISBN 0-19-853789-1
- James Norris (1998), Markov Chains, Cambridge University Press. ISBN 0-521-63396-6
- Springer Pólya (1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz", Mathematische Annalen, 84(1-2):149–160, March 1921.
- Pal Révész (1990), Random walk in random and non-random environments, World Scientific Pub Co. ISBN 981-02-0237-7
- Wolfgang Woess (2000), Random walks on infinite graphs and groups, Cambridge tracts in mathematics 138, Cambridge University Press. ISBN 0-521-55292-3
- Mackenzie, Dana, "Taking the Measure of the Wildest Dance on Earth", Science, Vol. 290, 8 December 2000.
- G. Weiss Aspects and Applications of the Random Walk, North-Holland, 1994.
- D. Ben-Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, 2000.
- "Numb3rs Blog." Department of Mathematics. 29 April 2006. Northeastern University. 12 December 2007 http://www.atsweb.neu.edu/math/cp/blog/?id=137&month=04&year=2006&date=2006-04-29.
External links






























![{\displaystyle {\begin{aligned}\langle k^{2}\rangle &=\sum _{k=0}^{N}k^{2}P(k;N)\\&=\left({\frac {1}{2}}\right)^{N}\sum _{k=1}^{N}(k-1+1)N{\binom {N-1}{k-1}}\\&=\left({\frac {1}{2}}\right)^{N}N\left[\sum _{k=2}^{N}(N-1){\binom {N-2}{k-2}}+\sum _{k=1}^{N}{\binom {N-1}{k-1}}\right]\\&=\left({\frac {1}{2}}\right)^{N}N\left[(N-1)2^{N-2}+2^{N-1}\right]\\&={\frac {N^{2}}{4}}+{\frac {N}{4}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cee1855871d21244e12e4d45699b2f190cd4fa9)







![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)






































![{\displaystyle {\bar {\Phi }}(s,L)=1+\Sigma _{c=1}^{[L/2]}(-1)^{c}{\bar {h}}(s,c;L)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2a2e01113b04c5f18bfab060312eca0caf1cec6)







