Talk:Parsec

Precision

“ It is therefore 360×60×60/2π AU = 206,264.806 247 AU = 3.085 677 581 31×10¹⁶ m = ~3.26 light-years. ”

I was trying to correct the precision of this calculation, but I think it is only a (close) approximation anyway, using the fact that tan(θ)~=θ for small θ. So, I have trimmed the number of significant digits.
Ray Spalding 17:49, 19 Mar 2004 (UTC)

The computation offered here is not immediately clear. I think the use of the approximation tan(θ) ~= θ for small θ is acceptable here, but we should either mention this as a whole, or leave out any form of computation. I prefer the latter, that is, to just state that a parsec is approximately ... km / miles / etc . without any calculations.

Maurice Termeer 08:21, 27 Mar 2006 (UTC)

Parsec

For the non-astronomers among us, how many miles is a parsec? From a crossword puzzle clue, I'm guessing 19 billion miles. Is that right?

One lightyear = ~5.88 × 10¹² miles

One parsec    = ~3.26 lightyears
              = ~(3.26 × 5.88) × 1012 miles
              = ~19.2 × 1012 miles

— Preceding unsigned comment added by 65.35.122.133 (talk • contribs) 16:07, 25 November 2004

So if you're talking British billion, yes that's right. If you're talking American billion, then no. It would be 19.2 trillion miles in American trillions. -- Derek Ross | Talk 16:21, 25 November 2004 (UTC)

Make that 'Traditional British billion' rather than 'modern British billion'. The Government and BBC would call the above number 19.2 trillion miles - see long scale for further information. Ian Cairns 19:23, 26 May 2005 (UTC)

Wouldn't it make more sense to state its approximate distance in normal units as 30.9 Pm instead of "trillions of kilometres", when names like trillion have different meanings to different people? Then again, why do we need this nonsense unit when expressing all spacial distances in metres with proper prefixes, such as kilo, mega, giga, tera, peta, exa, zetta, yotta can be used?

Whenever someone uses words like parsec and light year, it is always necessary to convert it normal SI units before it is understood. It seems like those who claim to be scientists, rather than acting in an enlightened manner, work in confusion. 68.105.199.216 (talk) 17:05, 7 October 2012 (UTC)

Debates like this are why I never use the words "billion" or "trillion" (or their higher-order relatives) in wiki articles. They are too ambiguous in meaning. Rhialto (talk) 13:15, 8 October 2012 (UTC)

When to call a billion a trillion

The article now contains the phrase:

and is approximately 19,131,554,073,600 (19 trillion) miles

Someone changed "trillion" to "billion", but I have changed it back. Ray Spalding 06:42, 26 September 2005 (UTC)

What I call a billion you call a trillion. It was probably not vandalism, just a product of the fact that there are two meanings of each of these words thanks to some bunch of clowns in the 17th century. We are probably stuck with this wittled-down trillion in English, though, so "trillion" let it stay. JIMp _talk·cont 01:21, 30 May 2008 (UTC)

After reading this discussion on the ways to read 10⁹, I located the article of long and short scales. I personally prefer the short scale (million=10⁶, billion=10⁹, trillion=10¹²) because of the logical word association of 'bi' meaning 2, 'tri' meaning 3, etc. Using billiard, and trilliard as terminology doesn't make much sense. With no disrespect intended, it's like assigning two different values for a single variable (x=1 and x=2 simultaneously). It's an anomaly; there should only be one use of the 'bi' prefix.

If we do away with the names, and just stick with the long terminology (thousand-million), we could say it is similar in respects to the Roman Numeral system, in which IV means 4, or 1 less than 5, and VI means 6, or 1 more than 5 (except we're working with exponents). Although the long number system appears to be designed for larger numbers, to me it just seems like a messy way to do things. On the other hand, if we use the short number system, it's very smooth and straight forward until we get to the really larger numbers. But by the time we reach long strings of numbers, we would simply drop the word descriptions.

My preference is for the most scientific numbering system (which is why I also wish that the world would do away with the Imperial units and the United States customary units). Having spent my entire life to this point in the U.S., it is natural that I would prefer the short scale over the long scale. Because of my ancestry, I have ties to continental Europe, which mainly uses the long scale. This means that I'd have to either learn both, or drop the terminology altogether and just use the mathematical values for numbers 10⁹ and larger (I doubt I will ever use 9 digits past decimal in all practical use).

Christopher, Salem, OR (talk) 00:44, 11 May 2010 (UTC)

Scientific notation of numbers in English the following are the equivalent notations :- Million is 1000x1000 =1,000,000 Milljard 1,000 x 1,000,000 or 1,000,000,000 in American financial terms a Billion A Mathematical Billion is a million millions (from bi-million) 1,000,000,000,000 in American financial terms this is a Trillion Billiard is 1,000 million millions 1,000,000,000,000,000 A Mathematical Trillion is thus tri-million 1,000,000 x 1,000,000,000 x 1,000,000 or 1,000,000,000,000,000,000 and such

Americans have routine problems working out distances in mathematics, or even scientific measurements - getting simply scientific and mathematics right (which incidentally they misspell as a singular discipline of Math, rather then disciplines of Maths). Their use of miles, when international scientists use Km for distances, and inability to deal with standard international mathematics has caused engineers routinely to cause problems missing targets in space, or having probes crash into Mars before their parachutes deploy or landing thrusters fire, and such - often blamed on a "Martian gremlin", much to the annoyance of their colleagues in the European Space Agency, and NASA leaders. This problem of miscalculating assets was found to be partially responsible for the worldwide financial crash of 2008/9 when American investment in NINJA (No Income, No Jobs or Assets) properties - which were sold on on worldwide markets - the debts and valuations in real terms were a fraction of a percentage of their overinflated real value and thus resulted in a massive right down of losses worldwide, as banks found they were under-capitalised with their loan-books overvalued, and debts exceeding their assets as a result. In the Republic of Ireland, Government bought bonds of banks, and became majority shareholder of many banks. Whole loan-books of buildings were created, which on the basis of the National Asset Management Agency Act became administered by civil servants and bank staff acquired. While the Bill was drafted I (Damon Matthew Wise), noting previous abandoned and unfinished buildings which were stripped down and unoccupied, thus unusable due to vandalism and squatters, proposes, and had included in the act provisions to have housing to be made available to local authourities and housing associations, and commercial and retail premises to Charities, voluntary and community groups and community/cottage industries on 5 or 10 year leases, rent free - the basis of this was to prevent complete loss of value - occupied buildings made available to sitting tenants who take care of them and make productive use will always increase in value, while unoccupied buildings lose value rapidly due to damage, decay and destruction and are most have no usable value within 6 to 18 months. — Preceding unsigned comment added by 109.77.233.95 (talk) 19:17, 31 January 2013 (UTC)

Would it not be better to avoid using ambiguous terms like "billion" and "trillion"? I recently tried to reword "trillion" in the above citation as "million million" - which is an unambiguous way of saying of 10¹² - only to be reverted. The problem, as already stated, is that "trillion" can mean either 10¹² (short scale) or 10¹⁸ (long scale), just as "billion" can mean either 10⁹ (short) or 10¹² (long). -- Glenn L (talk) 18:07, 1 April 2013 (UTC)

...except that the "long scale" is antiquated and deprecated in virtually every English-speaking country in the world (e.g. U.S., U.K., Commonwealth, etc.). A reader won't think that "trillion" refers to 10¹⁸ any more than they would think a British "penny" refers to 1/240th of a pound, instead of the modern 1/100th.

On the other hand, the term "million million" is confusing, because it's rarely encountered in common English language speech. Have you ever heard anyone state that the U.S. goverment's debt is 16 "million million" dollars? Of course not; that would confuse people. Using "trillion" (and assuming it to be understood as "short scale" trillion) confuses perhaps 0.01% of the readers. Using "million million" confuses the other 99.99% of readers. Shouldn't we use the terminology that causes the least amount of reader confusion? — Preceding unsigned comment added by Hatster301 (talk • contribs) 08:37, 2 April 2013 (UTC)

Discrepancy

This figure doesn't agree well with other figures in the article. A few lines from the top, it gives that 1 parsec = 3.08568×10¹⁶m
That equates to approximately 19,173,500,000,000 miles. This might seem a minor point, but if it's worth stating 12 significant figures in the article, then we've got to make sure that at least the 4th one agrees with the true value.Richard B 12:28, 8 October 2005 (UTC)

I also have a major issue with the precision given here.

• Info box says: "19.1735×10¹²" miles
• Main text says: "19,176,075,967,324.937" miles.

1. What is the point of giving a value to such precision if all other values in the article only have a precision of 4 or 5 decimal places?
2. The two values don't even agree with each other. If we round the precise - but not very accurate - number to the same precision as the other number, we get: 19.1761×10¹², but this value does not agree with the other, which is 19.1735×10¹².

Something is SERIOUSLY wrong with the accuracy here. Why bother giving it to 17 decimal places if it disagrees at the fourth place? -- B.D.Mills  (T, C) 06:23, 30 April 2008 (UTC)

Picture not to scale

I would recommend adding some kind of notice that the picture [1] depicting the method of how to calculate a Parsec is not to scale. I think it would be great if it could be added directly into the picture, but a note in the text would be fine, too.
--capnez 18:17, 4 Mar 2005 (UTC) 13:05, 4 Mar 2005 (UTC) EDIT: Updated my signature, I finally got an account!

Sure, it's to scale. Just for an extremely nearby star.  :-) --Doradus 10:52, 14 June 2006 (UTC)

No, it's not to scale. The angle as it appears in the diagram is far greater than one arcsecond! :-) 24.6.66.193 05:33, 5 August 2007 (UTC)

Discrepancy in Parsec Definition

There is a discrepancy on this page in the definition of a parsec. Near the top, it states: "The parsec is defined to be the distance from the Earth of a star that has a parallax of 1 arcsecond." But on the diagram towards the bottom, the parsec is labeled along the side of the triangle (which is the distance between the Sun and "D"), implying a parsec measures the distance between the Sun and another object, not between the Earth and that object.

Something doesn't add up. These two distances are quite different. What is the exact definition?

Globe199 13.00, 26 May 2005 (CDT)

Well, distance from the Solar System is the point. An object 1 parsec from the Sun is 206,265 AU away. Its distance from the Earth is 206,265 ± 1 AU; I wouldn't call that "quite different".

—wwoods 18:56, 26 May 2005 (UTC)

OK, so you're saying it doesn't really matter, since the distance is almost the same; we're talking about distance on a galactic scale, so ± 1 AU is negligible. Sounds good. On the other hand, at what point is parallax useless? The page on Deneb says the distance is between 1600 and 3200 light years because "...determination of distances at this range is very difficult because stars with such distances have negligible parallax."

Globe199 15.57, 26 May 2005 (CDT)

"On the other hand, at what point is parallax useless?"

All depends on how accurately you are able to measure the parallax. The ESA's Hipparcos mission was the most accurate that parallaxes had been measured. It measured the parallaxes of stars to a precision of a few milli-arcseconds. This means that it could measure distances reasonably accurately to a few hundred parsecs. The ESA's Gaia_probe scheduled for launch in 2011 aims to measure the parallaxes of bright stars to a few micro-arcseconds, and fainter stars to a slightly lower accuracy. With this, you could measure distances reasonably accurately to a few tens or even hundreds of thousands of parsecs. You could even measure parallaxes of some stars in some other galaxies.Richard B 11:34, 9 October 2005 (UTC)

..Earth's orbit as a baseline. The parsec follows naturally from this method, since the distance (in parsecs) is simply the reciprocal of the parallax angle (in arcseconds). But isn't the earth's orbit 2AU? So isn't this a factor of 2 out? Mat-C 04:36, 28 October 2005 (UTC)

That's exactly what I thought, but then I noticed that our diagram calls the "parallax angle" half the apparent motion of the nearby star. That makes it all work out. Seems a weird definition, but who can explain astronomers... --Doradus 10:54, 14 June 2006 (UTC)

I would like to know if it's the distance between our sun and the object, or us and the object. I know it seems neglible but I'd like a more accurate definition. As far as i know a parsec is the distance of an object with a heliocentric, stellar parralax of one second of arc....The distance of the object from what???

Hopeless

Unfortunately, this article is so very ugly and confusing that it really calls for a complete rewrite. leschatz 23:00, 29 January 2006 (UTC) I agree CPS

4,000,000,000,000,000 kilometers?

4,000,000,000,000,000 kilometers doesn't fit here, does it?

3.08567758 E+16 m = 4,000,000,000,000,000 kilometers is not correct. First of all there are two too many zeros. Secondly, if 1 km = 1000 m then the result would start with a 3, not a 4.

3.08567758 E+16 m = 30856775800000000 m = 30856775800000 km

Or am I missing something here???

Midavalo 8 March 2006

poorly explained

this article is good however the first paragraph which is crucial for the understanding the rest of the page is not very well explained. Actually it is pretty confusing. Fine a parsec is 3.26 ly but how that diagram determines that and what near star are you refering to? Krnchris 21:09, 15 May 2006 (UTC)

Any star. The imaginary star in the diagram is exactly 1 parsec away. -- Xerxes 00:24, 16 May 2006 (UTC)

Error in International Units calculation

I have ammended the number of metres in a parsec as the previous value was incorrect. The figure now matches that derived later in this page. Mrfunkyostrich 16:10, 11 August 2006 (UTC)

Is a parsec/secpar 299792458*3600*24*365.25*3.26156378 metres???

Han Solo

So how are we going to fit in Han's comment about doing "the Kessel Run in less than 12 parsecs" ? -- Beardo 01:04, 23 September 2006 (UTC)

I have heard this rationalized. If the objective of the Kessel Run is to complete a task in the minimum distance, then it makes perfect sense. (But I think Lucas screwed up.) Srain 02:12, 24 September 2006 (UTC)

Indeed, according to the (obviously rationalized) explanation of the Kessel Run, the objective is to smuggle spice from the mining colony Kessel through a nearby cluster of black holes and quantum singularities. Being such a difficult area to navigate, if you CAN do it you get away scott free, which leads to a competition between those that perform the "Kessel Run" to compare how efficiently they got through, i.e. how close they got to a black hole. Hence, 12 parsecs is a goood score. Still stupid though.

Shouldn't this reference be removed? After all, the technology behind hyperspace travel in Star Wars is unknown. If one thinks of warping space for faster-than-light travel, then a distance might be totally reasonable. To say it is "incorrect" seems a bit much, and without bringing up this question, it doesn't seem to have much use in the wiki entry.

The reason why Han Solo was boasting about that is because the Kessel Run has a greater distance than 12 parsecs, so when he was escaping from Imperials, he got so close to the one the Maw's blackholes that he actually warped distance.--209.244.43.103 (talk) 00:56, 3 October 2008 (UTC)

I think the mention is notable enough to belong in the article; and the article is not allowed to claim it's "incorrect" because the apologists, as above, may be right. But it could be "claimed to be incorrect" or "controversial". Tempshill (talk) 20:11, 18 November 2008 (UTC)

Does anyone watch the bonus features? They state in the bonus features that Han said that to brag about the capabilities of the Millennium Falcon's hyperdrive. They do in fact use warp technology, and the Millennium Falcon has a very good warp drive. They also say that the look on Ben's face is testament to the insanity of the statement. But it was not a mess up, it was the fact that he had a bitchen warp drive. John Holmes II (talk) 02:24, 23 December 2009 (UTC)

here how it works(this is the officail reasoning, you can check) the kessel run goes threw a black hole infested area. if you get too close to a black hole your screwed. he went so fast, he went past whats supposed to be the point of no return but was going so fast the ship just kept going. this shaved somedistance off. (end offical stuff) smuggelers and such knew what he ment but most people who dont realize what the kessel run is just think hes nuts, which would explain ben's look. 69.115.204.217 (talk) 02:29, 21 July 2010 (UTC)

I can't say what Lucas and his staff were thinking but see Length contraction and Time dilation. However, it's science fiction and they get to take some liberties. No one is complaining when he says the ship goes .5 past light speed. That would be faster that light travel(1.5*c). Who is to say what the effects of this are in that fictional world.

12.106.237.2 (talk) 14:24, 27 August 2010 (UTC)

Can someone remove the 'lol lucas messed it up lol?' It wasn't a mistake nor was it "intended as a joke." The Kessel Run is a competition between smugglers to plot a route that takes them near the black holes resulting in a shorter route, without falling out of minimum escape velocity and getting sucked in. It's not a typo so much as stupid people looking up the dictionary definition of parsec and assuming contextual error. 97.188.112.58 (talk) 19:43, 12 October 2010 (UTC)RLJ

These rationalizations don't fit the context though. The context of that line in the movie is Han Solo bragging about his, and I quote, "fast ship." Obi-Wan says he and Luke are looking for passage on a fast ship, and Han replies "Fast ship? You've never heard of the Millennium Falcon? It's the ship that made the Kessel Run in less than twelve parsecs." The context is clear: he's giving "12 parsecs" as an example of how fast his ship is. If he were talking about skipping through the space distorted by a black hole to cut down on the distance traveled, then he would be bragging about his own cleverness, not the speed of the ship. In addition, the "black hole shortcut" explanation is only given [i]later[/i], not in the movie but in the (non-canon) Expanded Universe, presumably for the sake of "fixing" what was, at the time of the movie, just a plain old error. Errors happen sometimes in science fiction, and it's OK to admit it. -- Anonymous — Preceding unsigned comment added by 207.111.162.65 (talk) 20:44, 16 January 2013 (UTC)

The explanation I've heard is that Solo was just throwing out technobabble to impress a couple of hicks from the sticks. He knew that a parsec was a unit of distance, but he didn't think that Luke and Ben knew that. That's why Ben winced skeptically after Han made the statement. He probably made up "the Kessel run" too. WaxTadpole (talk) 16:18, 31 May 2013 (UTC)

Picture Worth 1000 Words

Stellar parallax motion

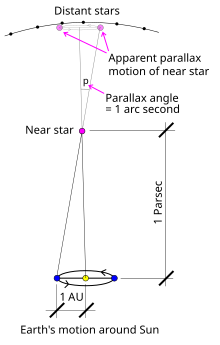
I've made an alternate version of the diagram which has "1 Parsec" "1 AU" and "1 arc second" depicted. I would like to replace the diagram, but appreciate some feedback first. Srain 02:31, 24 September 2006 (UTC)

Have I missed something?

I don't, given the rest of the article or picture, get this!

"There is no star whose parallax is more than 1 arcsecond."

When the parsec seems to be defined as 1 parsec per arcsecond parrallelax Frankenstien 04:21, 29 December 2006 (UTC)

No, parsecs are the reciprocal of parallax. 10 parsecs means 1/10 arcsecond parallax. No star is less than 3 parsecs away, so no star has more than 1/3 arcsecond parallax. --Doradus 15:10, 31 December 2006 (UTC)

Ahhh! Thank you, yes I would have more parsecs the closer I got! Frankenstien 11:37, 6 January 2007 (UTC)

Usage Missing Info

As a non-astronomer, I am still confused about how parsecs are used. First, it might be useful to explain that it is the reciprocal. Second, why would an astronomer use parsecs instead of light years, when the latter would seem to be more universal?

How so? The speed of light is a universal constant, but the length of earth's year doesn't have any universal meaning. So both units are somewhat arbitrary.

Both are parochial units. The light-year depends on the length of the Earth's year (actually, a precisely and arbitarily defined value that is very close to an Earth year). The parsec definition depends ultimately on Earth's orbital radius (actually a precisely (to the extent that the gravtational constant is known) and arbitarily defined value that is very close to Earth's orbital radius). Both are parochial and locally (on a galactic scale) defined units. Rhialto 06:26, 22 April 2007 (UTC)

Proposed WikiProject

Right now the content related to the various articles relating to measurement seems to be rather indifferently handled. This is not good, because at least 45 or so are of a great deal of importance to Wikipedia, and are even regarded as Vital articles. On that basis, I am proposing a new project at Wikipedia:WikiProject Council/Proposals#Measurement to work with these articles, and the others that relate to the concepts of measurement. Any and all input in the proposed project, including indications of willingness to contribute to its work, would be greatly appreciated. Thank you for your attention. John Carter 21:00, 2 May 2007 (UTC)

h^-1 Mpc

I've seen units of h^-1 Mpc a lot in googling some cosmology I was curious about; the Mpc is obviously megaparsecs, but what's the h^-1?

It could be Planck's constant. Rhialto 17:42, 21 May 2007 (UTC)

I should have mentioned it was being used to measure distances. If it was planck's constant, the units won't match up. --Starwed 19:10, 21 May 2007 (UTC)

h is the dimensionless magnitude of Hubble's constant divided by 100; that is, H₀ = 100h km/s/Mpc. Converting redshift to distance, in particular, involves Hubble's constant, which is not precisely known. If H₀ is 100 km/s/Mpc (as was once thought roughly correct), then the /h factor is unity and can be ignored; as the value estimated for H₀ decreases (it is now thought to be about 71 km/s/Mpc), the distance expressed with a /h factor increases. Ray Spalding 06:29, 22 May 2007 (UTC)

Would it make sense to add that into this article? --Starwed 19:16, 22 May 2007 (UTC)

Done. Ray Spalding 11:01, 23 May 2007 (UTC)

Parsec to Light-Year Conversion

Many people will visit this article looking for a conversion factor between parsecs and other common units. For some reason the conversion between parsecs and light-years was present on the discussion page but not in the article itself! I have therefore added the information to the article as light-years are also a very common way of specifying astronomical distances.

Actually, that conversion (and many many others) was in the infobox on the top right corner as soon as you load the page. Rhialto 12:16, 9 June 2007 (UTC)

Meaningfulness

I understand parsec is a useful unit for measurement when we observe objects from earth. Does the distance definition become arbitrary if the observer is not on earth or in earth orbit? --Voidvector 20:04, 29 September 2007 (UTC)

I think yes because the distance between the earth and the sun is part of the definition of the parsec. Egriffin 09:39, 18 October 2007 (UTC)

hi hello —Preceding unsigned comment added by 59.163.32.25 (talk) 14:17, 18 October 2007 (UTC)

Particle horizon's radius is 14 gpc???

okay so if the particle horizon's radius is 14 gpc, and each parsec is about 3.262 lightyears, that would make the radius of the observable universe around 45.7 lightyears. however, if the universe is around 13.7 billion years old, and is traveling a bit under the speed of light since, then our visible range of the universe couldn’t possibly extend out that far. so either cosmology is wrong, or the 14 gpc is wrong. —Preceding unsigned comment added by 70.228.68.29 (talk) 23:45, 25 November 2007 (UTC)

I think it is far more likely that your maths is wrong. You dropped the "giga". Rhialto (talk) 06:32, 26 November 2007 (UTC)

I don't see any "giga" in the question. What the heck is "gpc", anyway? Gene Nygaard (talk) 18:52, 26 November 2007 (UTC)

A "gpc" is a gigaparsec. Rhialto (talk) 20:35, 26 November 2007 (UTC)

We don't live in a special relativistic universe. It's not true that light travels a distance ct in a time t. That's only an approximation valid in some special cases. -- BenRG (talk) 16:57, 26 November 2007 (UTC)

Unless you are a scientist with a degree or three in astrophysics and several relevant articles in peer-reviewed journals, I think I'll take your opinion with a pinch of salt. If you are, cites please. Rhialto (talk) 18:48, 26 November 2007 (UTC)

Sorry for the late reply. I'm not an astrophysicist, but I've studied general relativity, which is necessary and sufficient for understanding this stuff. The best source of information about cosmology on the web is probably Ned Wright's site. "Expanding Confusion" by Tamara Davis and Charles Lineweaver is also worth reading, as is this Scientific American article by the same authors. This is a subject on which unfortunately a lot of seemingly reliable sources are flat wrong. As mentioned in the articles I linked, even a lot of professional astronomers get it wrong. I think the problem is that almost all introductions to special relativity spend most of their time on coordinate artifacts like time dilation, length contraction, relativity of simultaneity, and the speed c. They usually fail to clearly explain that (a) all of these concepts are meaningless except in the context of a family of inertial coordinate systems, and (b) there are no inertial coordinate systems in cosmology, or indeed coordinate systems of any kind anywhere in the real world. The result is a large number of people who think that the coordinate artifacts are general truths about nature, and use them to draw incorrect conclusions which they're confident enough to publish without checking against primary sources. For me the hardest part of learning general relativity was unlearning special relativity as it was taught to me and replacing it with coordinate-independent concepts (for example, that light travels along null geodesics and that elapsed proper time is the length of the worldline). -- BenRG (talk) 16:50, 29 January 2008 (UTC)

He means "Gpc". JIMp _talk·cont 01:30, 30 May 2008 (UTC)

Formula for parsec value

I have re-calculated the parsec value, using 149,597,870,691 m as the value for the Astronomical unit (sourced from wp article). I used the following as a formula in Excel:

1/ATAN(RADIANS(1/60/60))

That gives the number of au in one parsec, which is identical to 11 significant figures with the 360x60x60/2pi value shown in the diagram. Multiplying that number by the length of an au in m gives the pc length in m - 30,856,775,813,299,000 m. I suspect Excel will not happily calculate to more than 15 sig figs, so the last 3 zeroes can probably be considered spurious accuracy, as tools to calculate that many sig figs are not commonly available.

Rhialto (talk) 14:05, 27 November 2007 (UTC)

The 1976 IAU definition for the au is only good to +/- 30m, less than 11 significant figures, and its definition is a bit unhelpful: "the distance from the Sun at which a particle of negligible mass, in an unperturbed circular orbit, would have an orbital period of 365.2568983 days (a Gaussian year)." Using au*radian / arcsec rather than au/ATAN(arcsec) results in a proportional difference over 25 times smaller than the uncertainty of the definition of the au. Using the latter equation anyway and plugging in the +/- 30m precision to the interval arithmetic capacity of Frink, the precision of the definition of the parsec is 30,856,775,813,299,047 +/-6,187,944m, or between 30,856,775,807,111,103 and 30,856,775,819,486,992m, or more comprehensibly, 1 parsec = 3.08567758133(62)E16 m Using the alleged 2009 value in the Astronomical unit article with a supposed uncertainty of +/- 3m gives a value of 30,856,775,815,774,225 +/- 1,237,588m or 3.08567758158(12)E16 m

Enon (talk) 03:18, 25 February 2011 (UTC)

Non-standard display format?

Why are the SI units in the top right corner displayed in the form 30.857×10^12 km 30.857×10^15 m ? Scientific notation dictates they should be 3.0*10^13/16 respectively. --72.235.245.54 (talk) 08:54, 7 January 2008 (UTC)

It looks like the equally standard engineering notation to me, whereby the exponent is given the the smallest multiple of three which would make the main number greater or equal to one. If you want it changed, it'd be best to take it up on the talk page for Template:Unit_of_length instead of here, since that template affects many pages. Rhialto (talk) 10:57, 7 January 2008 (UTC)

Engineering notation as Rhialto points out. I almost switched {{Unit of length}} over to standard scientific notation when I overhauled it ... but I saw the light. Engineering notation nicely fits in with SI prefixes. 10¹⁵ metres ... that's a petametre ... easy. JIMp _talk·cont 01:29, 30 May 2008 (UTC)

"Misuse" section removed

I removed the following section because I consider it fandom irrelevant for a scientific article in an encyclopedia. This is not the Wokieepedia article about Parsec, you know. -- wr 87.139.81.19 (talk) 11:45, 17 April 2008 (UTC)

As a unit of astronomical distance, the parsec is mentioned in many science fiction stories. One use that stands out, however, is the remark by pilot Han Solo in Star Wars: A New Hope, that his spaceship is fast because it "made the Kessel Run in less than 12 parsecs." Later novels in this fictional universe have retconned Solo's remark to mean that the ship reached the planet Kessel in the shortest distance despite having to pass through a cluster of black holes.

It's odd to have an "earth-based" unit in a sci-fi world that doesn't even involve earth. --Voidvector (talk) 07:50, 26 August 2008 (UTC)

Well, no odder than their speaking English. Maybe "parsec" was a translator's error. -- BenRG (talk) 09:40, 26 August 2008 (UTC)

The section should be restored. It's a notable use of the term. Tempshill (talk) 20:11, 18 November 2008 (UTC)

Should not a policy be made about crapping up scientific articles with science fiction fantasy? I like Star Wars and such, but a parsec has an actual use in reality, and it isn't in starships going to such places that are parsecs away. I think the whole Science fiction section should be removed. 96.237.148.44 (talk) 04:52, 3 June 2009 (UTC)

I think it would be appropriate to include an "In Popular Culture" section which describes the use of the parsec in significant scifi works. Minetruly (talk) 01:54, 11 January 2010 (UTC)

Distant star

I guess that we are assuming that the 'distant star' in the picture is a fixed point? —Preceding unsigned comment added by 83.101.44.217 (talk) 08:43, 28 February 2009 (UTC)

Andromeda Galaxy

The Andromeda galaxy was previously described as being the most distant object from Earth visible to the naked eye. Bode's Galaxy (Messier 81) and the Triangulum galaxy (Messier 33) are both further away and visible to the naked eye, albeit under significantly better viewing conditions. Only the clause "the most distant object visible to the naked eye" was removed, as the rest of the sentence still makes sense. Epsilon Knight (talk) 20:08, 26 April 2009 (UTC)

Science fiction

Hm. Should we maybe remove this section? None of it is notable at all, and if we're gonna start listing every reference to parsecs in sci fi movies, series and novels, this could be one long list. -- Nils (talk) 13:35, 11 May 2009 (UTC)

This discussion happened about a year ago too, and the decision then was to remove it all. Rhialto (talk) 13:40, 11 May 2009 (UTC)

I think it would be appropriate to include an "In Popular Culture" section which describes the use of the parsec in significant scifi works. Minetruly (talk) 01:56, 11 January 2010 (UTC)

Parallax of the Sun

“ Other than the Sun, which has a parallax of 90 degrees ”

Not that it's incredibly important, but shouldn't this be 180 degrees? --Hasoan (talk) 01:34, 20 June 2009 (UTC)

No, as the article says in the History section, "The parallax of a star is half of the angular distance a star appears to move [...]" (emphasis on half added). This is because measuring the difference in angle of a star at 6-month intervals gives the angle at the apex of an isosceles triangle (with a base of 2 AU). That triangle is cut in half to get a right triangle (with base 1 AU), so that the tangent trig function can be applied. The sun, of course, is the limit case in which the isosceles triangle, with "apex" of 180 degrees, collapses into a straight line. But the parallax is still half that, or 90 degrees. Radius (talk) 03:05, 25 June 2009 (UTC)

Thousand million?

The section "Megaparsecs and gigaparsecs" uses the term "thousand million." Shouldn't that be "billion?" I'd change it, but I don't know if there's some reason specific to the field of astronomy it's phrased that way. —Preceding unsigned comment added by Minetruly (talk • contribs) 01:36, 11 January 2010 (UTC)

There is a difference between US billion (10⁹) and old-style English/European billion (10¹² - Europeans call 10⁹ a "milliard"). See billion. Due to that ambiguity, the term is best avoided. --Stephan Schulz (talk) 15:17, 9 February 2011 (UTC)

Proxima Centauri

Proxima Centauri article states that Proxima Centauri is 4.2 light-years away, not 1.29 parsecs. —Preceding unsigned comment added by 85.223.209.2 (talk) 08:13, 26 August 2010 (UTC)

A parsec is 3.26 light-years. 1.29 × 3.26 = 4.2, so both values are the same. --The High Fin Sperm Whale 17:36, 25 October 2010 (UTC)

Dots in image

I'm wondering what do the black dots in that curved line in the image mean... can anyone clarify this? --Waldir ^talk 19:29, 20 January 2011 (UTC)

They represent stars in the far background. --Stephan Schulz (talk) 22:58, 8 February 2011 (UTC)

I'm not sure why I didn't realize this before. Now that you've told me that, it seems obvious when looking at the image. I wonder if others would have the same doubts or if it was just a one-off case of inattention. Anyway, thanks for the clarification :) --Waldir ^talk 01:26, 9 February 2011 (UTC)

No problem. You're welcome. --Stephan Schulz (talk) 15:18, 9 February 2011 (UTC)

Confusing graph

I see there is some confusion about the diagram. To be honest, what I understood when I saw that diagram is that the form of calculation always reaches the distance of 1 parsec for any star or object, and that the parsec is not a fixed unit.

Reading the article, it's quite the opposite. But the main problem is that I had to reach this discussion page ("poorly explained" section) to understand the "1 parsec" caption in the diagram. I really don't think the diagram is self-explanatory.

Wouldn't it be better if the diagram showed the distance in a different manner, for example 'x parsecs' or 'n parsecs'? —Preceding unsigned comment added by 186.215.156.157 (talk) 19:38, 22 February 2011 (UTC)

Error in history

Quote from the article: "One of the oldest methods for astronomers to calculate the distance to a star was to record the difference in angle between two measurements of the position of the star in the sky. The first measurement was taken from the Earth on one side of the Sun, and the second was taken half a year later when the Earth was on the opposite side of the Sun."

This is plain WRONG! Because astronomy is as old as mankind, and in ancient times (before Kopernikus and Galilei), everybody believed in the GEOCENTRIC world, = the universe rotates around EARTH, not the sun! The article is based on a HELIOCENTRIC world-view, = the planets (of our solar system) rotate around the SUN, not the Earth! 93.219.151.5 (talk) 20:20, 12 May 2011 (UTC)

So I guess, "one of the oldest methods" should read, "one of the oldest accurate methods". How did geocentrists (attempt to) measure the distance to stars? Rwflammang (talk) 09:35, 13 May 2011 (UTC)

It's actually kind of correct. Until scientists discovered that the Earth revolves around the Sun, astronomy didn't really exist as a separate branch from astrology, and astrology wasn't concerned with measuring planetary or stellar distances. Rhialto (talk) 09:22, 15 May 2011 (UTC)

Ancient astronomers did indeed attempt to measure the distance to the sun and planets, and I believe, the stars as well. They were not very good at it. Read the Somnium Scipionis for some details. Rwflammang (talk) 18:57, 17 May 2011 (UTC)

Right triangle?

"The parsec is equal to the length of the adjacent side of an imaginary right triangle in space." -- I'm probably misunderstanding this completely, but the diagrams seem to imply that this only true when the object being measured is at ("on"?) the orbital pole? Ojw (talk) 22:22, 17 September 2011 (UTC)

Horizon scale

The article states that the present particle horizon in the Universe is 46.5 billion light-years, but the reference from Scientific American (in the same line) states 16 billion. Which one is correct? Should the value in the article be changed to that in the reference? joselotl (talk) 10 January 2012 —Preceding undated comment added 11:37, 10 January 2012 (UTC).

The linked article includes both the cosmic event horizon (16 billion ly) and the particle horizon (46 billion ly): "Consequently, the current distance to the most distant object we can see is about three times farther, or 46 billion light-years." -- JHunterJ (talk) 12:26, 10 January 2012 (UTC)

Distance from earth to the Andromeda Galaxy

There are two references in this article to the distance from earth to the Andromeda Galaxy: one for 2.61 Million Lightyears and one for 2.51 Million Lightyears. I don't know which one is correct but clearly both can't be... Pgcohen (talk) 00:32, 18 July 2012 (UTC)

Re-work for 2012 of the A.U.

The 2012 IAU conference finally agreed to scrap various earlier definitions and re-define the Astronomical Unit as a simple integral multiple of the meter. One parsec is therefore exactly 149,597,870.7 km / atan(1"). This is the exact value of one parsec. Of course since the inverse tangent of one arcsecond is a transcendental number, in decimal notation, the value has to be truncated at some point. So, for example, to the nearest micron, that come out to 30,856,775,815,155,429,770,405 microns. No one would ever need the value of a parsec to the nearest micron. This is just an example. It doesn't matter that you can do a "small angle" approximation here. That's just another method for truncating the precision.68.9.201.92 (talk) 20:54, 17 October 2012 (UTC)

I know we're in danger here of dancing on the head of a pin, but since we're talking about "exact" (always dangerous): the IAU page referenced below defines a parsec as "the distance at which one Astronomical Unit subtends an angle of one arcsecond". In other words, in an equilateral triangle with a base measuring 1au and having an apex with an included angle of 1 arcsecond, the perpendicular from the base to the apex measures one parsec. So the formula should be 0.5au / tan(0.5"). Windows 7's calculator makes this to be 30,856,775,814,853,233.543822509736376 m, which diverges from your value after the 10th significant figure (Libre Office spreadsheet makes it 30,856,775,814,853,200 so it obviously gives up after 15 digits but that's enough to support the point). Also, your calculation should have used tan, not atan. The aforementioned small angle approximation does mean they give close results at 1 arcsecond, of course --Gobbag (talk) 16:24, 31 August 2013 (UTC)

In Popular Culture

In Star Wars, The Millenium Falcon (fictional spaceship) is described as "the ship that made the Kessel Run in less than twelve parsecs". This should be added to the article.— Preceding unsigned comment added by 75.150.107.217 (talk • contribs) 17:06, 7 January 2013‎ (UTC)

Why? See also Wikipedia:"In popular culture" content. -- JHunterJ (talk) 17:40, 7 January 2013 (UTC)

I recommend a link under "See Also" pointing to the article on the Millennium Falcon - perhaps directly to the section titled "Depiction." So that when someone comes here looking for the parsec article who was motivated by the line in Star Wars, which is quite conceivably culturally significant in that many people first heard of a parsec thanks to the very widely viewed film, they can at least see an acknowledgement of the connection. Agreeable? Medleystudios72 (talk) 18:12, 4 April 2013 (UTC)

Astrometry: "Megaparsecs and gigaparsecs"???

Quoting from the article: "Astronomers typically measure the distances between neighbouring galaxies and galaxy clusters in megaparsecs." Perhaps a minor quibble, but it seems to me that the notion of actually "measuring distances" (as opposed to expressing them) on the order of megaparsecs and larger is, as of 2013, pretty darn meaningless given that the usage of parsecs within astronomy is intimately (and historically) tied to directly-observed parallax. The latest best such measurements was from Hipparcos, and was good only down to 1 milliarcsecond, and therefore itself was barely adequate for merely kiloparsec range(!). Should this not be noted in this section of the article? DWIII (talk) 06:26, 20 April 2013 (UTC)

Feel free to correct it! --Regards, Necessary Evil (talk) 02:02, 21 April 2013 (UTC)

Oh for heaven's sake

A parsec is 30.857×10^12 km. It's as simple as that.

https://www.iau.org/public/measuring/ — Preceding unsigned comment added by 71.212.78.121 (talk • contribs) 08:21, 26 June 2013‎ (UTC)

Design Error?

I quote: "ESA's Gaia satellite, ... , is intended to measure ... , producing errors of 10% in measurements as far as the Galactic Center". I guess the intention is not to on purpose produce errors of 10%, but rather a maximum of 10%. — Preceding unsigned comment added by Hilmer B (talk • contribs) 11:21, 16 July 2013 (UTC)

Comment on Broomwick's input.

It is true that it is difficult to measure distances with parallax at ranges greater than 1,000 pc (High precision parallax collecting satellite, Hipparcos). However the astronomical distance measurement is a ladder, where e.g. parallax measurements determinate the distances to standard candles like Cepheids. Cepheid variable stars in turn gives the distance to their parent galaxy, and so on. The frequency of a certain type of Cepheid, compared to the observed luminosity, gives a calculation from parsecs to megaparsecs.

The real popularity of the light-year is not because of "advancement of astrophysics and cosmology into worlds far from the Solar System". It is so much easier to explain the light-year to a layman, than the parsec. Since readers of astronomy textbooks & scientific literature, plus members of established institutions are familiar with the parsec, it is used by them. Popular science medias use the light-year instead. --Regards, Necessary Evil (talk) 21:25, 6 August 2013 (UTC)