Quaquaversal tiling

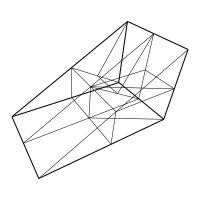
The quaquaversal tiling is a nonperiodic tiling of the euclidean 3-space introduced by John Conway and Charles Radin. The basic solid tiles are half prisms arranged in a pattern that relies essentially on their previous construct, the pinwheel tiling. The rotations relating these tiles belong to the group G(6,4) generated by two rotations of order 6 and 4 whose axes are perpendicular to each other. These rotations are dense in SO(3).

References

• Conway, John H.; Radin, Charles (1998), "Quaquaversal tilings and rotations", Inventiones Mathematicae, 132 (1): 179–188, Bibcode:1998InMat.132..179C, doi:10.1007/s002220050221, MR 1618635, S2CID 14194250.
• Radin, Charles; Sadun, Lorenzo (1998), "Subgroups of SO(3) associated with tilings", Journal of Algebra, 202 (2): 611–633, doi:10.1006/jabr.1997.7320, MR 1617675.

External links

• A picture of a quaquaversal tiling
• Charles Radin page at the University of Texas