Antiprism

Set of uniform antiprisms

Type	uniform polyhedron
Faces	2 n-gons, 2n triangles
Edges	4n
Vertices	2n
Conway polyhedron notation	An
Vertex configuration	3.3.3.n
Schläfli symbol	{ }⊗{n}^[1] s{2,2n} sr{2,n}
Coxeter diagrams
Symmetry group	D_nd, [2⁺,2n], (2*n), order 4n
Rotation group	D_n, [2,n]⁺, (22n), order 2n
Dual polyhedron	trapezohedron
Properties	convex, semi-regular vertex-transitive
Net

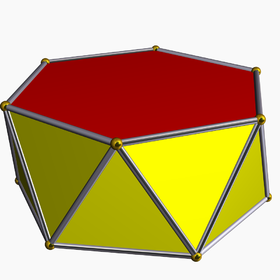
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles. Antiprisms are a subclass of the prismatoids and are a (degenerate) type of snub polyhedron.

Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.

In the case of a regular n-sided base, one usually considers the case where its copy is twisted by an angle ⁠180°/n⁠. Extra regularity is obtained when the line connecting the base centers is perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.

Uniform antiprism

A uniform antiprism has, apart from the base faces, 2n equilateral triangles as faces. As a class, the uniform antiprisms form an infinite series of vertex-uniform polyhedra, as do the uniform prisms. For n = 2 we have as degenerate case the regular tetrahedron as a digonal antiprism, and for n = 3 the non-degenerate regular octahedron as a triangular antiprism.

The dual polyhedra of the antiprisms are the trapezohedra. Their existence was discussed and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes as they satisfy the same conditions on vertices as the Archimedean solids.

Family of uniform n-gonal antiprisms
v
t
e
Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	...	Apeirogonal antiprism
Polyhedron image							...
Spherical tiling image							Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Schlegel diagrams

A3	A4	A5	A6	A7	A8

Cartesian coordinates

Cartesian coordinates for the vertices of a right antiprism with n-gonal bases and isosceles triangles are

\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)

with k ranging from 0 to 2n − 1; if the triangles are equilateral,

2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.

Volume and surface area

Let a be the edge-length of a uniform antiprism. Then the volume is

V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}a^{3}

and the surface area is

A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.

Related polyhedra

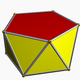
There are an infinite set of truncated antiprisms, including a lower-symmetry form of the truncated octahedron (truncated triangular antiprism). These can be alternated to create snub antiprisms, two of which are Johnson solids, and the snub triangular antiprism is a lower symmetry form of the icosahedron.

Antiprisms
				...
s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,2n}
Truncated antiprisms
				...
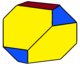
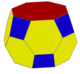
ts{2,4}	ts{2,6}	ts{2,8}	ts{2,10}	ts{2,2n}
Snub antiprisms
J₈₄	Icosahedron	J₈₅	Irregular...
				...
ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}	ss{2,2n}

Symmetry

The symmetry group of a right n-sided antiprism with regular base and isosceles side faces is D_nd of order 4n, except in the case of a tetrahedron, which has the larger symmetry group T_d of order 24, which has three versions of D_2d as subgroups, and the octahedron, which has the larger symmetry group O_h of order 48, which has four versions of D_3d as subgroups.

The symmetry group contains inversion if and only if n is odd.

The rotation group is D_n of order 2n, except in the case of a tetrahedron, which has the larger rotation group T of order 12, which has three versions of D₂ as subgroups, and the octahedron, which has the larger rotation group O of order 24, which has four versions of D₃ as subgroups.

Star antiprism

5/2-antiprism			5/3-antiprism
9/2-antiprism		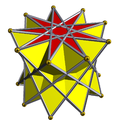9/4-antiprism		9/5-antiprism

Uniform star antiprisms are named by their star polygon bases, {p/q}, and exist in prograde and retrograde (crossed) solutions. Crossed forms have intersecting vertex figures, and are denoted by inverted fractions, p/(p - q) instead of p/q, e.g. 5/3 instead of 5/2.

In the retrograde forms but not in the prograde forms, the triangles joining the star bases intersect the axis of rotational symmetry.

Some retrograde star antiprisms with regular star polygon bases cannot be constructed with equal edge lengths, so are not uniform polyhedra. Star antiprism compounds also can be constructed where p and q have common factors; thus a 10/4 antiprism is the compound of two 5/2 star antiprisms.

Star antiprisms by symmetry, up to 12
Symmetry group	Uniform stars			Other stars
d_4d [2⁺,8] (2*5)				3.3/2.3.4
d_5h [2,5] (*225)	3.3.3.5/2			3.3/2.3.5
d_5d [2⁺,10] (2*5)	3.3.3.5/3
d_6d [2⁺,12] (2*6)				3.3/2.3.6
d_7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
d_7d [2⁺,14] (2*7)	3.3.3.7/3
d_8d [2⁺,16] (2*8)	3.3.3.8/3	3.3.3.8/5
d_9h [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
d_9d [2⁺,18] (2*9)	3.3.3.9/5
d_10d [2⁺,12] (2*10)	3.3.3.10/3
d_11h [2,11] (*2.2.11)	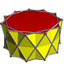3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
d_11d [2⁺,22] (2*11)	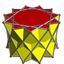3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
d_12d [2⁺,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...

References

Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisma and antiprisms

^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c

External links

[1] N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c

[1]