Equal-loudness contour

ISO equal-loudness contours with frequency in Hz

An equal-loudness contour is a measure of sound pressure level, over the frequency spectrum, for which a listener perceives a constant loudness when presented with pure steady tones. The unit of measurement for loudness levels is the phon and is arrived at by reference to equal-loudness contours. By definition, two sine waves of differing frequencies are said to have equal-loudness level measured in phons if they are perceived as equally loud by the average young person without significant hearing impairment.

The Fletcher–Munson curves are one of many sets of equal-loudness contours for the human ear, determined experimentally by Harvey Fletcher and Wilden A. Munson, and reported in a 1933 paper entitled "Loudness, its definition, measurement and calculation" in the Journal of the Acoustical Society of America. Fletcher–Munson curves have been superseded and incorporated into newer standards. The definitive curves are those defined in ISO 226 from the International Organization for Standardization, which are based on a review of modern determinations made in various countries.

Amplifiers often feature a "loudness" button, known technically as loudness compensation, that boosts low and high-frequency components of the sound. These are intended to offset the apparent loudness fall-off at those frequencies, especially at lower volume levels. Boosting these frequencies produces a flatter equal-loudness contour that appears to be louder even at low volume, preventing the perceived sound from being dominated by the mid-frequencies where the ear is most sensitive.

Fletcher–Munson curves

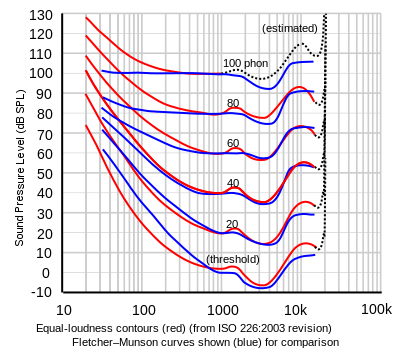
The first research on the topic of how the ear hears different frequencies at different levels was conducted by Fletcher and Munson in 1933. Until recently, it was common to see the term Fletcher–Munson used to refer to equal-loudness contours generally, even though a re-determination was carried out by Robinson and Dadson in 1956, which became the basis for an ISO 226 standard.

The generic term equal-loudness contours is now preferred, of which the Fletcher–Munson curves are now a sub-set, and especially since a 2003 survey by ISO redefined the curves in a new standard.

Experimental determination

The human auditory system is sensitive to frequencies from about 20 Hz to a maximum of around 20,000 Hz, although the upper hearing limit decreases with age. Within this range, the human ear is most sensitive between 2 and 5 kHz, largely due to the resonance of the ear canal and the transfer function of the ossicles of the middle ear.

Fletcher and Munson first measured equal-loudness contours using headphones (1933). In their study, test subjects listened to pure tones at various frequencies and over 10 dB increments in stimulus intensity. For each frequency and intensity, the listener also listened to a reference tone at 1000 Hz. Fletcher and Munson adjusted the reference tone until the listener perceived that it had the same loudness as the test tone. Loudness, being a psychological quantity, is difficult to measure, so Fletcher and Munson averaged their results over many test subjects to derive reasonable averages. The lowest equal-loudness contour represents the quietest audible tone—the absolute threshold of hearing. The highest contour is the threshold of pain.

Churcher and King carried out a second determination in 1937, but their results and Fletcher and Munson's showed considerable discrepancies over parts of the auditory diagram.

In 1956 Robinson and Dadson produced a new experimental determination that they believed was more accurate. It became the basis for a standard (ISO 226) that was considered definitive until 2003, when ISO revised the standard on the basis of recent assessments by research groups worldwide.

Recent revision aimed at more precise determination – ISO 226:2023

Perceived discrepancies between early and more recent determinations led the International Organization for Standardization (ISO) to revise the standard curves in ISO 226. They did this in response to recommendations in a study coordinated by the Research Institute of Electrical Communication, Tohoku University, Japan. The study produced new curves by combining the results of several studies—by researchers in Japan, Germany, Denmark, UK, and the US. (Japan was the greatest contributor with about 40% of the data.)

This has resulted in the recent acceptance of a new set of curves standardized as ISO 226:2003. The report comments on the surprisingly large differences, and the fact that the original Fletcher–Munson contours are in better agreement with recent results than the Robinson–Dadson, which appear to differ by as much as 10–15 dB, especially in the low-frequency region, for reasons not explained.

According to the ISO report, the Robinson–Dadson results were the odd one out, differing more from the current standard than did the Fletcher–Munson curves. The report states that it is fortunate that the 40-phon Fletcher–Munson curve on which the A-weighting standard was based turns out to have been in agreement with modern determinations.

The report also comments on the large differences apparent in the low-frequency region, which remain unexplained. Possible explanations are:

• The equipment used was not properly calibrated.
• The criteria used for judging equal loudness at different frequencies had differed.
• Subjects were not properly rested for days in advance, or were exposed to loud noise in traveling to the tests, which tensed the tensor tympani and stapedius muscles controlling low-frequency mechanical coupling.

Side versus frontal presentation

Real-life sounds from a reasonably distant source arrive as planar wavefronts. If the source of sound is directly in front of the listener, then both ears receive equal intensity, but at frequencies above about 1 kHz the sound that enters the ear canal is partially reduced by the head shadow, and also highly dependent on reflection off the pinna (outer ear). Off-centre sounds result in increased head masking at one ear, and subtle changes in the effect of the pinna, especially at the other ear. This combined effect of head-masking and pinna reflection is quantified in a set of curves in three-dimensional space referred to as head-related transfer functions (HRTFs). Frontal presentation is now regarded as preferable when deriving equal-loudness contours, and the latest ISO standard is specifically based on frontal and central presentation.

Because no HRTF is involved in normal headphone listening, equal-loudness curves derived using headphones are valid only for the special case of what is called side-presentation, which is not how we normally hear.

The Robinson–Dadson determination used loudspeakers, and for a long time the difference from the Fletcher–Munson curves was explained partly on the basis that the latter used headphones. However, the ISO report actually lists the latter as using compensated headphones, though it doesn't make clear how Robinson–Dadson achieved compensation.

Headphones versus loudspeaker testing

Good headphones, well sealed to the ear, provide a flat low-frequency pressure response to the ear canal, with low distortion even at high intensities. At low frequencies, the ear is purely pressure-sensitive, and the cavity formed between headphones and ear is too small to introduce modifying resonances. Headphone testing is, therefore, a good way to derive equal-loudness contours below about 500 Hz, though reservations have been expressed about the validity of headphone measurements when determining the actual threshold of hearing, based on the observation that closing off the ear canal produces increased sensitivity to the sound of blood flow within the ear, which the brain appears to mask in normal listening conditions. At high frequencies, headphone measurement becomes unreliable, and the various resonances of pinnae (outer ears) and ear canals are severely affected by proximity to the headphone cavity.

With speakers, the opposite is true. A flat low-frequency response is hard to obtain—except in free space high above ground, or in a very large and anechoic chamber that is free from reflections down to 20 Hz. Until recently, it was not possible to achieve high levels at frequencies down to 20 Hz without high levels of harmonic distortion. Even today, the best speakers are likely to generate around 1 to 3% of total harmonic distortion, corresponding to 30 to 40 dB below fundamental. This is not good enough, given the steep rise in loudness (rising to as much as 24 dB per octave) with frequency revealed by the equal-loudness curves below about 100 Hz. A good experimenter must ensure that trial subjects really hear the fundamental and not harmonics—especially the third harmonic, which is especially strong as a speaker cone's travel becomes limited as its suspension reaches the limit of compliance. A possible way around the problem is to use acoustic filtering, such as by resonant cavity, in the speaker setup. A flat free-field high-frequency response up to 20 kHz, on the other hand, is comparatively easy to achieve with modern speakers on-axis. These effects must be considered when comparing results of various attempts to measure equal-loudness contours.

Relevance to sound level and noise measurements

The A-weighting curve—in widespread use for noise measurement—is said to have been based on the 40-phon Fletcher–Munson curve. However, research in the 1960s demonstrated that determinations of equal-loudness made using pure tones are not directly relevant to our perception of noise. This is because the cochlea in our inner ear analyzes sounds in terms of spectral content, each "hair-cell" responding to a narrow band of frequencies known as a critical band. The high-frequency bands are wider in absolute terms than the low-frequency bands, and therefore "collect" proportionately more power from a noise source. However, when more than one critical band is stimulated, the signals to the brain add the various bands to produce the impressions of loudness. For these reasons equal-loudness curves derived using noise bands show an upwards tilt above 1 kHz and a downward tilt below 1 kHz when compared to the curves derived using pure tones.

Various weighting curves were derived in the 1960s, in particular as part of the DIN 4550 standard for audio quality measurement, which differed from the A-weighting curve, showing more of a peak around 6 kHz. These gave a more meaningful subjective measure of noise on audio equipment, especially on the newly invented compact cassette tape recorders with Dolby noise reduction, which were characterized by a noise spectrum dominated by the higher frequencies.

BBC Research conducted listening trials in an attempt to find the best weighting curve and rectifier combination for use when measuring noise in broadcast equipment, examining the various new weighting curves in the context of noise rather than tones, confirming that they were much more valid than A-weighting when attempting to measure the subjective loudness of noise. This work also investigated the response of human hearing to tone-bursts, clicks, pink noise and a variety of other sounds that, because of their brief impulsive nature, do not give the ear and brain sufficient time to respond. The results were reported in BBC Research Report EL-17 1968/8 entitled The Assessment of Noise in Audio Frequency Circuits.

The ITU-R 468 noise weighting curve, originally proposed in CCIR recommendation 468, but later adopted by numerous standards bodies (IEC, BSI, JIS, ITU) was based on the research, and incorporates a special quasi-peak detector to account for our reduced sensitivity to short bursts and clicks. It is widely used by Broadcasters and audio professionals when they measure noise on broadcast paths and audio equipment, so they can subjectively compare equipment types with different noise spectra and characteristics.

See also

• A-weighting
• Audio quality measurement
• Audiogram
• CCIR (ITU) 468 Noise Weighting
• dB(A)
• ITU-R 468 noise weighting
• Listener fatigue
• Luminosity function, the same concept in vision
• Mel scale
• Pure tone audiometry
• Robinson–Dadson curves
• Sound level meter
• Weighting filter

References

• Audio Engineer's Reference Book, 2nd Ed., 1999, edited Michael Talbot Smith, Focal Press.
• An Introduction to the Psychology of Hearing 5th ed, Brian C.J. Moore, Elsevier Press.

External links

• ISO Standard
• Precise and Full-range Determination of Two-dimensional Equal Loudness Contours
• Fletcher–Munson is not Robinson–Dadson (PDF)
• Full Revision of International Standards for Equal-Loudness Level Contours (ISO 226)
• Test your hearing – A tool for measuring your equal-loudness contours
• Equal-loudness contour measurements in detail
• Evaluation of Loudness-level weightings and LLSEL JASA
• A Model of Loudness Applicable to Time-Varying Sounds AESJ Article