Jump to content

Nitrogen-vacancy center

From Wikipedia, the free encyclopedia
Simplified atomic structure of the NV center

The nitrogen-vacancy center (N-V center or NV center) is one of numerous photoluminescent point defects in diamond. Its most explored and useful properties include its spin-dependent photoluminescence (which enables measurement of the electronic spin state using optically detected magnetic resonance), and its relatively long (millisecond) spin coherence at room temperature, lasting up to milliseconds.[1] The NV center energy levels are modified by magnetic fields,[2] electric fields,[3] temperature,[4] and strain,[5] which allow it to serve as a sensor of a variety of physical phenomena. Its atomic size and spin properties can form the basis for useful quantum sensors.[6]

NV centers enable nanoscale measurements of magnetic and electric fields, temperature, and mechanical strain with improved precision. External perturbation sensitivity makes NV centers ideal for applications in biomedicine—such as single-molecule imaging and cellular process modeling.[7] NV centers can also be initialized as qubits and enable the implementation of quantum algorithms and networks. It has also been explored for applications in quantum computing (e.g. for entanglement generation[8]), quantum simulation,[9] and spintronics.[10]

Structure

[edit]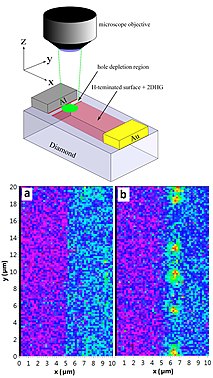
Bottom images are spatial photoluminescence (PL) maps before and after application of +20 V voltage to a planar Schottky diode. The top image outlines the experiment. The PL maps reveal the conversion of individual NV0 centers into NV− centers that appear as bright dots.[11]

The nitrogen-vacancy center is a point defect in the diamond lattice. It consists of a nearest-neighbor pair of a nitrogen atom, which substitutes for a carbon atom, and a lattice vacancy.

Two charge states of this defect, neutral NV0 and negative NV−, are known from spectroscopic studies using optical absorption,[12][13] photoluminescence (PL),[14] electron paramagnetic resonance (EPR)[15][16][17] and optically detected magnetic resonance (ODMR),[18] which can be viewed as a hybrid of PL and EPR; most details of the structure originate from EPR. The nitrogen atom on one hand has five valence electrons. Three of them are covalently bonded to the carbon atoms, while the other two remain non-bonded and are called a lone pair. The vacancy on the other hand has three unpaired electrons. Two of them form a quasi covalent bond and one remains unpaired. The overall symmetry, however, is axial (trigonal C3V); one can visualize this by imagining the three unpaired vacancy electrons continuously exchanging their roles.

The NV0 thus has one unpaired electron and is paramagnetic. However, despite extensive efforts, electron paramagnetic resonance signals from NV0 avoided detection for decades until 2008. Optical excitation is required to bring the NV0 defect into the EPR-detectable excited state; the signals from the ground state are presumably too broad for EPR detection.[19]

The NV0 centers can be converted into NV− by changing the Fermi level position. This can be achieved by applying external voltage to a p-n junction made from doped diamond, e.g., in a Schottky diode.[11]

In the negative charge state NV−, an extra electron is located at the vacancy site forming a spin S=1 pair with one of the vacancy electrons. This extra electron induces spin triplet ground states of the form |3A⟩ and excited states of the form |3E⟩.[20] There is an additional metastable state that exists between these spin triplets, that often manifests as a singlet. These states play a crucial role in enabling ground state depletion (GSD) microscopy.[21] As in NV0, the vacancy electrons are "exchanging roles" preserving the overall trigonal symmetry. This NV− state is what is commonly, and somewhat incorrectly, called "the nitrogen-vacancy center". The neutral state is not generally used for quantum technology.

The NV centers are randomly oriented within a diamond crystal. Ion implantation techniques can enable their artificial creation in predetermined positions.[22]

Production

[edit]
Main article: Crystallographic defects in diamond

Nitrogen-vacancy centers are typically produced from single substitutional nitrogen centers (called C or P1 centers in diamond literature) by irradiation followed by annealing at temperatures above 700 °C.[12] A wide range of high-energy particles is suitable for such irradiation, including electrons, protons, neutrons, ions, and gamma photons. Irradiation produces lattice vacancies, which are a part of NV centers. Those vacancies are immobile at room temperature, and annealing is required to move them. Single substitutional nitrogen produces strain in the diamond lattice;[23] it therefore efficiently captures moving vacancies,[24] producing the NV centers.

Production of nitrogen-vacancy centers in diamond may require several steps. First, nitrogen must be introduced into the diamond lattice which can be accomplished via ion implantation or CVD delta doping. Secondly, vacancies must be introduced, which can be accomplished via laser irradiation, ion implantation, or electron irradiation. Alternatively, during the nitrogen introduction step, vacancies may also be introduced. Finally, a high-temperature annealing step can help promote NV formation.[25]

During chemical vapor deposition of diamond, a small fraction of single substitutional nitrogen impurity (typically <0.5%) traps vacancies generated as a result of the plasma synthesis. Such nitrogen-vacancy centers are preferentially aligned to the growth direction.[26][27] Delta doping of nitrogen during CVD growth can be used to create two-dimensional ensembles of NV centers near the diamond surface for enhanced sensing[28] or simulation.[29]

Diamond is notorious for having a relatively large lattice strain. Strain splits and shifts optical transitions from individual centers resulting in broad lines in the ensembles of centers.[12][30] Special care is taken to produce extremely sharp NV lines (line width ~10 MHz)[31] required for most experiments: high-quality, pure natural or better synthetic diamonds (type IIa) are selected. Many of them already have sufficient concentrations of grown-in NV centers and are suitable for applications. If not, they are irradiated by high-energy particles and annealed. Selection of a certain irradiation dose allows tuning the concentration of produced NV centers such that individual NV centers are separated by micrometre-large distances. Then, individual NV centers can be studied with standard optical microscopes or, better, near-field scanning optical microscopes having sub-micrometre resolution.[18][32]

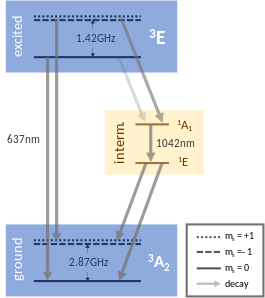
Schematic energy level structure of the NV center. Electron transitions between the ground 3A and excited 3E states, separated by 1.945 eV (637 nm), produce absorption and luminescence. The 3A state is split by 2.87 GHz[33][34] and the 3E state by 1.42 GHz.[35] Numbers 0, ±1 indicate spin quantum number ms; splitting due to the orbital degeneracy is not shown.

Energy level structure

[edit]

The NV center has a ground-state triplet (3A), an excited-state triplet (3E) and two intermediate-state singlets (1A and 1E).[note 1][36][37] Both 3A and 3E contain ms = ±1 spin states, in which the two electron spins are aligned (either up, such that ms = +1 or down, such that ms = -1), and an ms = 0 spin state where the electron spins are antiparallel. Due to the magnetic interaction, the energy of the ms = ±1 states is higher than that of the ms = 0 state. 1A and 1E only contain a spin state singlet each with ms = 0.

If an external magnetic field is applied along the defect axis (the axis which aligns with the nitrogen atom and the vacancy) of the NV center, it does not affect the ms = 0 states, but it splits the ms = ±1 levels (Zeeman effect). Similarly the following other properties of the environment influence the energy level diagram (further discussed under #Effects of external fields):

  1. Amplitude and orientation of a static magnetic field splits the ms = ±1 levels in the ground and excited states.
  2. Amplitude and orientation of elastic (strain) or electric fields[38][39] have a much smaller but also more complex effects on the different levels.
  3. Continuous-wave microwave radiation (applied in resonance with the transition between ms = 0 and (one of the) ms = ±1 states) changes the population of the sublevels within the ground and excited state.[39]
  4. A tunable laser can selectively excite certain sublevels of the ground and excited states.[39][40]
  5. Surrounding spins and spin–orbit interaction will modulate the magnetic field experienced by the NV center.
  6. Temperature and pressure affect different parts of the spectrum including the shift between ground and excited states.

The above-described energy structure[note 2] is by no means exceptional for a defect in diamond or other semiconductor.[41] It was not this structure alone, but a combination of several favorable factors (previous knowledge, easy production, biocompatibility, simple initialisation, use at room temperature etc.) which suggested the use of the NV center as a qubit and quantum sensor.

Optical properties

[edit]
Optical absorption and emission of the NV− center at room temperature.

NV centers emit bright red light (3E→3A transitions), if excited off-resonantly by visible green light (3A →3E transitions). This can be done with convenient light sources such as argon or krypton lasers, frequency doubled Nd:YAG lasers, dye lasers, or He-Ne lasers. Excitation can also be achieved at energies below that of zero phonon emission.[42]

As the relaxation time from the excited state is small (~10 ns),[43][44] the emission happens almost instantly after the excitation. At room temperature the NV center's optical spectrum exhibits no sharp peaks due to thermal broadening. However, cooling the NV centers with liquid nitrogen or liquid helium dramatically narrows the lines down to a width of a few MHz. At low temperature it also becomes possible to specifically address the zero-phonon line (ZPL).

An important property of the luminescence from individual NV centers is its high temporal stability. Whereas many single-molecular emitters bleach (i.e. change their charge state and become dark) after emission of 106–108 photons, bleaching is unlikely for NV centers at room temperature.[45][32] Strong laser illumination, however, may also convert some NV− into NV0 centers.[14]

Because of these properties, the ideal technique to address the NV centers is confocal microscopy, both at room temperature and at low temperature.

State manipulation

[edit]
Spin dynamics in the NV center in diamond. The primary transition between the ground and excited state triplets is spin conserving. Decay via the intermediate singlets gives rise to spin polarization by converting spin from ms = ±1 to ms = 0. Both absorption and emission wavelengths are indicated,[46] since they differ due to Stokes shift.[47][48] Furthermore, the effect of a static magnetic field B0 along the defect axis and the resulting Zeeman shift is indicated. Here, γnv refers to the gyromagnetic ratio of the NV center. In many applications two of the ground-state levels are then used as a qubit.[49] Transitions in this effective two-level system, may be induced using a microwave field. 3E-1A and 1E-3A are non-radiative transitions.

Optical spin manipulation

[edit]

Optical transitions must preserve the total spin and occur only between levels of the same total spin. Specifically, transitions between the ground and excited states (with equal spin) can be induced using a green laser with a wavelength of 546 nm. Transitions 3E→1A and 1E→3A are non-radiative, while 1A →1E has both a non-radiative and infrared decay path.

The diagram on the right shows the multi-electronic states of the NV center labeled according to their symmetry (E or A) and their spin state (3 for a triplet (S=1) and 1 for a singlet (S=0)). There are two triplet states and two intermediate singlet states.[50]

Spin-state initialisation

[edit]

An important property of the non-radiative transition between 3E and 1A is that it is stronger for ms = ±1 and weaker for ms = 0. This provides the basis a very useful manipulation strategy, which is called spin state initialisation (or optical spin-polarization). To understand the process, first consider an off-resonance excitation which has a higher frequency (typically 2.32 eV (532 nm)) than the frequencies of all transitions and thus lies in the vibronic bands for all transitions. By using a pulse of this wavelength, one can excite all spin states from 3A to 3E. An NV center in the ground state with ms = 0 will be excited to the corresponding excited state with ms = 0 due to the conservation of spin. Afterwards it decays back to its original state. For a ground state with ms = ±1, the situation is different. After the excitation, it has a relatively high probability to decay into the intermediate state 1A by non-radiative transition[note 3][51] and further into the ground state with ms = 0. After many cycles, the state of the NV center (independently of whether it started in ms = 0 or ms = ±1) will end up in the ms = 0 ground state. This process can be used to initialize the quantum state of a qubit for quantum information processing or quantum sensing.

Sometimes the polarisability of the NV center is explained by the claim that the transition from 1E to the ground state with ms = ±1 is small, compared to the transition to ms = 0. However, it has been shown that the comparatively low decay probability for ms = 0 states w.r.t. ms = ±1 states into 1A is enough to explain the polarization.[52]

Effects of external fields

[edit]

Microwave spin manipulation

[edit]

The energy difference between the ms = 0 and ms = ±1 states corresponds to the microwave regime. Population can be transferred between the states by applying a resonant magnetic field perpendicular to the defect axis. Numerous dynamic effects (spin echo, Rabi oscillations, etc.) can be exploited by applying a carefully designed sequence of microwave pulses.[53][54][55][56][57] Such protocols are rather important for the practical realization of quantum computers. By manipulating the population, it is possible to shift the NV center into a more sensitive or stable state.[58][59] Its own resulting fluctuating fields may also be used to influence the surrounding nuclei[60] or protect the NV center itself from noise.[61] This is typically done using a wire loop (microwave antenna) which creates an oscillating magnetic field.[62]

Optical manipulation

[edit]

There are inherent difficulties in achieving miniaturization and effective error reduction in microwave and radio frequency driven spin manipulation techniques. This poses special challenge on application of spin based quantum sensors on sensing electric and magnetic field or any physical phenomena at nanoscale level. The recent developments in microwave-free and optically driven methods[63][64] pave the way towards energy efficient and coherent quantum sensing. This technique is based on coherent mapping of the spin states of the Nitrogen nucleus to that of the NV center under the application of external magnetic field transverse to the NV symmetry axis. The optical pumping then prepares the system in a coherent superposition state which is the key element in a quantum network.

Influence of external factors

[edit]

If a magnetic field is oriented along the defect axis it leads to Zeeman splitting separating the ms = +1 from the ms = -1 states. This technique is used to lift the degeneracy and use only two of the spin states (usually the ground states with ms = -1 and ms = 0) as a qubit. Population can then be transferred between them using a microwave field. In the specific instance that the magnetic field reaches 1027 G (or 508 G) then the ms = –1 and ms = 0 states in the ground (or excited) state become equal in energy (Ground/Excited State Level Anticrossing). The following strong interaction results in so-called spin polarization, which strongly affects the intensity of optical absorption and luminescence transitions involving those states.[35]

Importantly, this splitting can be modulated by applying an external electric field,[38][39] in a similar fashion to the magnetic field mechanism outlined above, though the physics of the splitting is somewhat more complex. Nevertheless, an important practical outcome is that the intensity and position of the luminescence lines is modulated. Strain has a similar effect on the NV center as electric fields.[65]

There is an additional splitting of the ms = ±1 energy levels, which originates from the hyperfine interaction between surrounding nuclear spins and the NV center. These nuclear spins create magnetic and electric fields of their own leading to further distortions of the NV spectrum (see nuclear Zeeman and quadrupole interaction). Also the NV center's own spin–orbit interaction and orbital degeneracy leads to additional level splitting in the excited 3E state.

Temperature and pressure directly influence the zero-field term of the NV center leading to a shift between the ground and excited state levels.

The Hamiltonian, a quantum mechanical equation describing the dynamics of a system, which shows the influence of different factors on the NV center can be found below.

Although it can be challenging, all of these effects are measurable, making the NV center a perfect candidate for a quantum sensor.[59]

Charge state manipulation

[edit]

It is also possible to switch the charge state of the NV center (i.e. between NV−, NV+ and NV0) by applying a gate voltage.[66] The gate voltage electrically shifts the Fermi level at the diamond surface and changes its surface band bending. Upon varying the gate voltage, individual centers are allowed to switch from an unknown non-fluorescent state to the neutral charge state NV0. The ensemble of centers can be transitioned from NV0 to the qubit state NV−. The diamond surface termination additionally influences the charge state of near-surface NV centers. Oxygen termination is known to stabilize the NV−state by reducing surface conductivity and mitigating band bending[67] This improves charge state stability and coherence. In a similar capacity, nitrogen termination also affects surface properties and can optimize NV centers for specific sensing applications.

Optical excitation methods additionally play a role in charge state manipulation. Illumination with specific wavelengths can induce transitions between charge states. Near-infrared light at 1064 nm has been shown to convert NV0 to NV−, enhancing photoluminescence.[68]

Applications

[edit]
Scanning thermal microscopy using the NV center.
(a) Schematics of experimental setup. An electric current is applied to the arms of an AFM cantilever (phosphorus-doped Si, P:Si) and heats up the end section above the tip (intrinsic Si, i-Si). The bottom lens excites a diamond nanocrystal with a green laser light and collects photoluminescence (PL). The crystal hosts an NV center and is attached to the AFM tip. A wire on the sample surface serves as the microwave source (mw). The temperature of the cantilever Th is determined from the applied current and voltage.
(b) ODMR spectra of the NV center at three temperatures. The line splitting originates from a ~1 mT applied magnetic field.
(c) Thermal conductivity image of a gold letter E on sapphire. White circles indicate features that do not correlate with the AFM topography. (d) PL image of the AFM cantilever end and tip where the diamond nanocrystal appears as the bright spot. (e) Zoomed PL image of the NV center in d.[69]

The spectral shape and intensity of the optical signals from the NV− centers are sensitive to external perturbation, such as temperature, strain, electric and magnetic field. However, the use of spectral shape for sensing those perturbation is impractical, as the diamond would have to be cooled to cryogenic temperatures to sharpen the NV− signals. A more realistic approach is to use luminescence intensity (rather than lineshape), which exhibits a sharp resonance when a microwave frequency is applied to diamond that matches the splitting of the ground-state levels. The resulting optically detected magnetic resonance signals are sharp even at room temperature, and can be used in miniature sensors. Such sensors can detect magnetic fields of a few nanotesla[70] or electric fields of about 10 V/cm[71] at kilohertz frequencies after 100 seconds of averaging. This sensitivity allows detecting a magnetic or electric field produced by a single electron located tens of nanometers away from an NV− center.

Using the same mechanism, the NV− centers were employed in scanning thermal microscopy to measure high-resolution spatial maps of temperature and thermal conductivity (see image).[69]

Because the NV center is sensitive to magnetic fields, it is being actively used in scanning probe measurements to study myriad condensed matter phenomena both through measuring a spatially varying magnetic field or inferring local currents in a device.[72][73][74][75][76]

Another possible use of the NV− centers is as a detector to measure the full mechanical stress tensor in the bulk of the crystal. For this application, the stress-induced splitting of the zero-phonon-line is exploited, and its polarization properties.[77] A robust frequency-modulated radio receiver using the electron-spin-dependent photoluminescence that operated up to 350 °C demonstrates the possibility for use in extreme conditions.[78]

In addition to the quantum optical applications, luminescence from the NV− centers can be applied for imaging biological processes, such as fluid flow in living cells.[79][80] This application relies on good compatibility of diamond nano-particles with the living cells and on favorable properties of photoluminescence from the NV− centers (strong intensity, easy excitation and detection, temporal stability, etc.). Compared with large single-crystal diamonds, nanodiamonds are cheap (about US$1 per gram) and available from various suppliers. NV− centers are produced in diamond powders with sub-micrometre particle size using the standard process of irradiation and annealing described above. Due to the relatively small size of nanodiamond, NV centers can be produced by irradiating nanodiamond of 100 nm or less with medium energy H+ beam. This method reduces the required ion dose and reaction, making it possible to mass-produce fluorescent nanodiamonds in ordinary laboratory.[81] Fluorescent nanodiamond produced with such method is bright and photostable, making it excellent for long-term, three dimensional tracking of single particle in living cell.[82] Those nanodiamonds are introduced in a cell, and their luminescence is monitored using a standard fluorescence microscope.[83]

Stimulated emission from the NV− center has been demonstrated, though it could be achieved only from the phonon side-band (i.e. broadband light) and not from the ZPL. For this purpose, the center has to be excited at a wavelength longer than ~650 nm, as higher-energy excitation ionizes the center.[84]

The first continuous-wave room-temperature maser has been demonstrated.[85][86] It used 532-nm pumped NV− centers held within a high Purcell factor microwave cavity and an external magnetic field of 4300 G. Continuous maser oscillation generated a coherent signal at ~9.2 GHz.

The NV center can have a very long spin coherence time approaching the second regime.[87] This is advantageous for applications in quantum sensing[88] and quantum communication.[89] Disadvantageous for these applications is the long radiative lifetime (~12 ns[90][91] ) of the NV center and the strong phonon sideband in its emission spectrum. Both issues can be addressed by putting the NV center in an optical cavity.[92]

Historical remarks

[edit]

The microscopic model and most optical properties of ensembles of the NV− centers have been firmly established in the 1970s based on the optical measurements combined with uniaxial stress[12] and on the electron paramagnetic resonance.[15][16] However, a minor error in EPR results (it was assumed that illumination is required to observe NV− EPR signals) resulted in the incorrect multiplicity assignments in the energy level structure. In 1991 it was shown that EPR can be observed without illumination,[17] which established the energy level scheme shown above. The magnetic splitting in the excited state has been measured only recently.[35]

The characterization of single NV− centers has become a very competitive field nowadays, with many dozens of papers published in the most prestigious scientific journals. One of the first results was reported back in 1997.[18] In that paper, it was demonstrated that the fluorescence of single NV− centers can be detected by room-temperature fluorescence microscopy and that the defect shows perfect photostability. Also one of the outstanding properties of the NV center was demonstrated, namely room-temperature optically detected magnetic resonance.

See also

[edit]

Notes

[edit]
  1. ^ Group theory results are used to take into account the symmetry of the diamond crystal, and so the symmetry of the NV itself. Followingly, the energy levels are labeled according to group theory, and in particular are labelled after the irreducible representations of the C3V symmetry group of the defect center, A1, A2, and E. The "3" in 3A2 and 3E as well as the "1" in 1A1 and 1E represent the number of allowable ms spin states, or the spin multiplicity, which range from –S to S for a total of 2S+1 possible states. If S = 1, ms can be −1, 0, or 1.
  2. ^ The energy level structure of the NV center was established by combining optically detected magnetic resonance (ODMR), electron paramagnetic resonance (EPR) and theoretical results, as shown in the figure. In particular, several theoretical works have been done, using the Linear Combination of Atomic Orbitals (LCAO) approach,[citation needed] to build the electronic orbitals to describe the possible quantum states, looking at the NV center as a molecule.
  3. ^ This is a phenomenon called intersystem crossing (ISC). It happens at an appreciable rate because the energy curve in function of the position of the atoms for the excited ms = ±1 state intersects the curve for the 1A state. Therefore, for some instant during the vibrational relaxation that the ions undergo after the excitement, it is possible for the spin to flip with little or no energy required in the transition.

References

[edit]
  1. ^ Hanson, R.; Gywat, O.; Awschalom, D. D. (2006-10-26). "Room-temperature manipulation and decoherence of a single spin in diamond". Physical Review B. 74 (16): 161203. arXiv:quant-ph/0608233. Bibcode:2006PhRvB..74p1203H. doi:10.1103/PhysRevB.74.161203. S2CID 5055366.
  2. ^ Maze, J. R.; Stanwix, P. L.; Hodges, J. S.; Hong, S.; Taylor, J. M.; Cappellaro, P.; Jiang, L.; Dutt, M. V. Gurudev; Togan, E.; Zibrov, A. S.; Yacoby, A.; Walsworth, R. L.; Lukin, M. D. (October 2008). "Nanoscale magnetic sensing with an individual electronic spin in diamond". Nature. 455 (7213): 644–647. Bibcode:2008Natur.455..644M. doi:10.1038/nature07279. ISSN 1476-4687. PMID 18833275.
  3. ^ Dolde, F.; Fedder, H.; Doherty, M. W.; Nöbauer, T.; Rempp, F.; Balasubramanian, G.; Wolf, T.; Reinhard, F.; Hollenberg, L. C. L.; Jelezko, F.; Wrachtrup, J. (June 2011). "Electric-field sensing using single diamond spins". Nature Physics. 7 (6): 459–463. arXiv:1103.3432. Bibcode:2011NatPh...7..459D. doi:10.1038/nphys1969. hdl:11858/00-001M-0000-0027-768E-1. ISSN 1745-2481. S2CID 119287960.
  4. ^ Kucsko, G.; Maurer, P. C.; Yao, N. Y.; Kubo, M.; Noh, H. J.; Lo, P. K.; Park, H.; Lukin, M. D. (August 2013). "Nanometre-scale thermometry in a living cell". Nature. 500 (7460): 54–58. arXiv:1304.1068. Bibcode:2013Natur.500...54K. doi:10.1038/nature12373. ISSN 1476-4687. PMC 4221854. PMID 23903748.
  5. ^ Maze, J R; Gali, A; Togan, E; Chu, Y; Trifonov, A; Kaxiras, E; Lukin, M D (2011-02-28). "Properties of nitrogen-vacancy centers in diamond: the group theoretic approach". New Journal of Physics. 13 (2): 025025. arXiv:1010.1338. Bibcode:2011NJPh...13b5025M. doi:10.1088/1367-2630/13/2/025025. ISSN 1367-2630. S2CID 16820460.
  6. ^ Degen, C. L.; Reinhard, F.; Cappellaro, P. (2017-07-25). "Quantum sensing". Reviews of Modern Physics. 89 (3): 035002. arXiv:1611.02427. Bibcode:2017RvMP...89c5002D. doi:10.1103/RevModPhys.89.035002. hdl:1721.1/124553. S2CID 2555443.
  7. ^ Savage, Neil (2021-03-25). "Quantum diamond sensors". Nature. 591 (7851): S37 – S37. doi:10.1038/d41586-021-00742-4. ISSN 0028-0836.
  8. ^ Bernien, H.; Hensen, B.; Pfaff, W.; Koolstra, G.; Blok, M. S.; Robledo, L.; Taminiau, T. H.; Markham, M.; Twitchen, D. J.; Childress, L.; Hanson, R. (May 2013). "Heralded entanglement between solid-state qubits separated by three metres". Nature. 497 (7447): 86–90. arXiv:1212.6136. Bibcode:2013Natur.497...86B. doi:10.1038/nature12016. ISSN 1476-4687. PMID 23615617. S2CID 4383784.
  9. ^ Choi, Soonwon; Choi, Joonhee; Landig, Renate; Kucsko, Georg; Zhou, Hengyun; Isoya, Junichi; Jelezko, Fedor; Onoda, Shinobu; Sumiya, Hitoshi; Khemani, Vedika; von Keyserlingk, Curt; Yao, Norman Y.; Demler, Eugene; Lukin, Mikhail D. (March 2017). "Observation of discrete time-crystalline order in a disordered dipolar many-body system". Nature. 543 (7644): 221–225. arXiv:1610.08057. Bibcode:2017Natur.543..221C. doi:10.1038/nature21426. ISSN 1476-4687. PMC 5349499. PMID 28277511.
  10. ^ Awschalom, David D.; Bassett, Lee C.; Dzurak, Andrew S.; Hu, Evelyn L.; Petta, Jason R. (2013-03-08). "Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors". Science. 339 (6124): 1174–1179. Bibcode:2013Sci...339.1174A. doi:10.1126/science.1231364. ISSN 0036-8075. PMID 23471400. S2CID 206545890.
  11. ^ a b Schreyvogel, C.; Polyakov, V.; Wunderlich, R.; Meijer, J.; Nebel, C. E. (2015). "Active charge state control of single N-V centres in diamond by in-plane Al-Schottky junctions". Scientific Reports. 5: 12160. Bibcode:2015NatSR...512160S. doi:10.1038/srep12160. PMC 4503995. PMID 26177799.
  12. ^ a b c d Davies, G.; Hamer, M. F. (1976). "Optical Studies of the 1.945 eV Vibronic Band in Diamond". Proceedings of the Royal Society of London A. 348 (1653): 285. Bibcode:1976RSPSA.348..285D. doi:10.1098/rspa.1976.0039. S2CID 93303167.
  13. ^ Mita, Y. (1996). "Change of absorption spectra in type-Ib diamond with heavy neutron irradiation". Physical Review B. 53 (17): 11360–11364. Bibcode:1996PhRvB..5311360M. doi:10.1103/PhysRevB.53.11360. PMID 9982752.
  14. ^ a b Iakoubovskii, K.; Adriaenssens, G. J.; Nesladek, M. (2000). "Photochromism of vacancy-related centres in diamond" (PDF). Journal of Physics: Condensed Matter. 12 (2): 189. Bibcode:2000JPCM...12..189I. doi:10.1088/0953-8984/12/2/308. S2CID 250820432. Archived from the original (PDF) on 2016-03-04. Retrieved 2013-03-04.
  15. ^ a b Loubser, J. H. N.; van Wyk, J. A. (1977). "Electron Spin Resonance in Annealed Type 1b Diamond". Diamond Research. 11: 4–7. ISSN 0070-4679.
  16. ^ a b Loubser, J. H. N.; van Wyk, J. A. (1978). "Electron spin resonance in the study of diamond". Reports on Progress in Physics. 41 (8): 1201. Bibcode:1978RPPh...41.1201L. doi:10.1088/0034-4885/41/8/002. S2CID 250898303.
  17. ^ a b Redman, D.; Brown, S.; Sands, R.; Rand, S. (1991). "Spin dynamics and electronic states of N-V centers in diamond by EPR and four-wave-mixing spectroscopy". Physical Review Letters. 67 (24): 3420–3423. Bibcode:1991PhRvL..67.3420R. doi:10.1103/PhysRevLett.67.3420. PMID 10044729.
  18. ^ a b c Gruber, A.; et al. (1997). "Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers" (PDF). Science. 276 (5321): 2012–2014. doi:10.1126/science.276.5321.2012. Archived from the original (PDF) on 2017-03-16. Retrieved 2017-03-16.
  19. ^ Felton, S.; et al. (2008). "Electron paramagnetic resonance studies of the neutral nitrogen vacancy in diamond". Physical Review B. 77 (8): 081201. Bibcode:2008PhRvB..77h1201F. doi:10.1103/PhysRevB.77.081201. S2CID 122354274.
  20. ^ Ho, Kin On; Wong, King Cho; Leung, Man Yin; Pang, Yiu Yung; Leung, Wai Kuen; Yip, King Yau; Zhang, Wei; Xie, Jianyu; Goh, Swee K.; Yang, Sen (2021-06-28). "Recent developments of quantum sensing under pressurized environment using the nitrogen vacancy (NV) center in diamond". Journal of Applied Physics. 129 (24). doi:10.1063/5.0052233. ISSN 0021-8979.
  21. ^ Han, Kyu Young; Kim, Seong Keun; Eggeling, Christian; Hell, Stefan W. (2010-08-11). "Metastable Dark States Enable Ground State Depletion Microscopy of Nitrogen Vacancy Centers in Diamond with Diffraction-Unlimited Resolution". Nano Letters. 10 (8): 3199–3203. doi:10.1021/nl102156m. hdl:11858/00-001M-0000-0012-D53F-5. ISSN 1530-6984.
  22. ^ Awschalom, D. D.; Epstein, R.; Hanson, R. (2007). "Diamond Age of Spintronics". Scientific American. 297 (4): 84–91. Bibcode:2007SciAm.297d..84A. doi:10.1038/scientificamerican1007-84. PMID 17926759.
  23. ^ Lang, A. R.; et al. (1991). "On the Dilatation of Synthetic Type Ib Diamond by Substitutional Nitrogen Impurity". Philosophical Transactions of the Royal Society A. 337 (1648): 497–520. Bibcode:1991RSPTA.337..497L. doi:10.1098/rsta.1991.0135. S2CID 54190787.
  24. ^ Iakoubovskii, K.; Adriaenssens, G. J. (2001). "Trapping of vacancies by defects in diamond". Journal of Physics: Condensed Matter. 13 (26): 6015. Bibcode:2001JPCM...13.6015I. doi:10.1088/0953-8984/13/26/316. S2CID 250804678.
  25. ^ Smith, Jason M.; Meynell, Simon A.; Jayich, Ania C. Bleszynski; Meijer, Jan (2019-11-01). "Colour centre generation in diamond for quantum technologies". Nanophotonics. 8 (11): 1889–1906. Bibcode:2019Nanop...8..196S. doi:10.1515/nanoph-2019-0196. ISSN 2192-8614. S2CID 207968005.
  26. ^ Edmonds, A.; d’Haenens-Johansson, U.; Cruddace, R.; Newton, M.; Fu, K. -M.; Santori, C.; Beausoleil, R.; Twitchen, D.; Markham, M. (2012). "Production of oriented nitrogen-vacancy color centers in synthetic diamond". Physical Review B. 86 (3): 035201. arXiv:1112.5757. Bibcode:2012PhRvB..86c5201E. doi:10.1103/PhysRevB.86.035201. S2CID 118609894.
  27. ^ Pham, L. M.; Bar-Gill, N.; Le Sage, D.; Belthangady, C.; Stacey, A.; Markham, M.; Twitchen, D. J.; Lukin, M. D.; Walsworth, R. L. (2012-09-06). "Enhanced metrology using preferential orientation of nitrogen-vacancy centers in diamond". Physical Review B. 86 (12): 121202. arXiv:1207.3363. Bibcode:2012PhRvB..86l1202P. doi:10.1103/PhysRevB.86.121202. S2CID 3283919.
  28. ^ Hughes, Lillian B.; Zhang, Zhiran; Jin, Chang; Meynell, Simon A.; Ye, Bingtian; Wu, Weijie; Wang, Zilin; Davis, Emily J.; Mates, Thomas E.; Yao, Norman Y.; Mukherjee, Kunal; Bleszynski Jayich, Ania C. (2023-02-01). "Two-dimensional spin systems in PECVD-grown diamond with tunable density and long coherence for enhanced quantum sensing and simulation". APL Materials. 11 (2): 021101. arXiv:2211.02282. Bibcode:2023APLM...11b1101H. doi:10.1063/5.0133501. ISSN 2166-532X. S2CID 253370730.
  29. ^ Davis, E. J.; Ye, B.; Machado, F.; Meynell, S. A.; Wu, W.; Mittiga, T.; Schenken, W.; Joos, M.; Kobrin, B.; Lyu, Y.; Wang, Z.; Bluvstein, D.; Choi, S.; Zu, C.; Jayich, A. C. Bleszynski (June 2023). "Probing many-body dynamics in a two-dimensional dipolar spin ensemble". Nature Physics. 19 (6): 836–844. Bibcode:2023NatPh..19..836D. doi:10.1038/s41567-023-01944-5. ISSN 1745-2481. PMC 10264245. PMID 37323805.
  30. ^ Quantum Information Processing with Diamond. Elsevier. 2014. doi:10.1016/c2013-0-16329-5. ISBN 978-0-85709-656-2. S2CID 119422670.
  31. ^ Tamarat, Ph.; et al. (2006). "Stark Shift Control of Single Optical Centers in Diamond". Physical Review Letters. 97 (8): 083002. arXiv:quant-ph/0607170. Bibcode:2006PhRvL..97h3002T. doi:10.1103/PhysRevLett.97.083002. PMID 17026299. S2CID 33870769.
  32. ^ a b Kuhn, S.; et al. (2001). "Diamond colour centres as a nanoscopic light source for scanning near-field optical microscopy". Journal of Microscopy. 202 (1): 2–6. doi:10.1046/j.1365-2818.2001.00829.x. PMID 11298860. S2CID 26077916.
  33. ^ Loubser, J. H. N.; van Wyk, J. A. (1977). "Electron Spin Resonance in Annealed Type 1b Diamond". Diamond Research. 11: 4–7. ISSN 0070-4679.
  34. ^ Loubser, J. H. N.; van Wyk, J. A. (1978). "Electron spin resonance in the study of diamond". Reports on Progress in Physics. 41 (8): 1201. Bibcode:1978RPPh...41.1201L. doi:10.1088/0034-4885/41/8/002. S2CID 250898303.
  35. ^ a b c Fuchs, G. D.; et al. (2008). "Excited-State Spectroscopy Using Single Spin Manipulation in Diamond". Physical Review Letters. 101 (1): 117601. arXiv:0806.1939. Bibcode:2008PhRvL.101k7601F. doi:10.1103/PhysRevLett.101.117601. PMID 18851332. S2CID 24822943.
  36. ^ Manson, N. B.; Harrison, J. P.; Sellars, M. J. (2006-09-21). "Nitrogen-vacancy center in diamond: Model of the electronic structure and associated dynamics". Physical Review B. 74 (10): 104303. arXiv:cond-mat/0601360. Bibcode:2006PhRvB..74j4303M. doi:10.1103/PhysRevB.74.104303.
  37. ^ Gali, Ádám (2019-11-01). "Ab initio theory of the nitrogen-vacancy center in diamond". Nanophotonics. 8 (11): 1907–1943. arXiv:1906.00047. Bibcode:2019Nanop...8..154G. doi:10.1515/nanoph-2019-0154. S2CID 202236167.
  38. ^ a b Tamarat, Ph.; et al. (2006). "Stark Shift Control of Single Optical Centers in Diamond". Physical Review Letters. 97 (8): 083002. arXiv:quant-ph/0607170. Bibcode:2006PhRvL..97h3002T. doi:10.1103/PhysRevLett.97.083002. PMID 17026299. S2CID 33870769.
  39. ^ a b c d Tamarat, Ph.; et al. (2008). "Spin-flip and spin-conserving optical transitions of the nitrogen-vacancy centre in diamond". New Journal of Physics. 10 (4): 045004. Bibcode:2008NJPh...10d5004T. doi:10.1088/1367-2630/10/4/045004. hdl:1969.1/179402. S2CID 37554428.
  40. ^ Santori, C.; et al. (2006). "Coherent Population Trapping of Single Spins in Diamond under Optical Excitation". Physical Review Letters. 97 (24): 247401. arXiv:quant-ph/0607147. Bibcode:2006PhRvL..97x7401S. doi:10.1103/PhysRevLett.97.247401. hdl:2318/103560. PMID 17280321. S2CID 14264923.
  41. ^ Aharonovich, I.; et al. (2009). "Enhanced single-photon emission in the near infrared from a diamond color center". Physical Review B. 79 (23): 235316. Bibcode:2009PhRvB..79w5316A. doi:10.1103/PhysRevB.79.235316. S2CID 37867189.
  42. ^ De Weerdt, F.; Collins, A. T.; Zugik, M.; Connor, A. (2005). "Sub-threshold excitation of luminescene of defects in diamonds". Journal of Physics: Condensed Matter. 50 (17): 8005. Bibcode:2005JPCM...17.8005D. doi:10.1088/0953-8984/17/50/018. S2CID 97620201.
  43. ^ Collins, A. T.; Thomaz, M. F.; Jorge, M. I. B. (1983). "Luminescence decay time of the 1.945 eV centre in type Ib diamond". Journal of Physics C. 16 (11): 2177. Bibcode:1983JPhC...16.2177C. doi:10.1088/0022-3719/16/11/020.
  44. ^ Hanzawa, H.; Nisida, Y.; Kato, T. (1997). "Measurement of decay time for the NV centre in Ib diamond with a picosecond laser pulse". Diamond and Related Materials. 6 (11): 1595. Bibcode:1997DRM.....6.1595H. doi:10.1016/S0925-9635(97)00037-X.
  45. ^ Gruber, A.; et al. (1997). "Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers" (PDF). Science. 276 (5321): 2012–2014. doi:10.1126/science.276.5321.2012. Archived from the original (PDF) on 2017-03-16. Retrieved 2017-03-16.
  46. ^ Gordon, Luke; Weber, Justin R.; Varley, Joel B.; Janotti, Anderson; Awschalom, David D.; Van de Walle, Chris G. (2013-10-01). "Quantum computing with defects". MRS Bulletin. 38 (10): 802–807. arXiv:1003.1754. Bibcode:2013MRSBu..38..802G. doi:10.1557/mrs.2013.206.
  47. ^ Rogers, L. J.; Doherty, M. W.; Barson, M. S. J.; Onoda, S.; Ohshima, T.; Manson, N. B. (2015-01-01). "Singlet levels of the NV − centre in diamond". New Journal of Physics. 17 (1): 013048. arXiv:1407.6244. Bibcode:2015NJPh...17a3048R. doi:10.1088/1367-2630/17/1/013048. S2CID 43745993.
  48. ^ Rogers, L. J.; Armstrong, S.; Sellars, M. J.; Manson, N. B. (2008). "Infrared emission of the NV centre in diamond: Zeeman and uniaxial stress studies". New Journal of Physics. 10 (10): 103024. arXiv:0806.0895. Bibcode:2008NJPh...10j3024R. doi:10.1088/1367-2630/10/10/103024. S2CID 42329227.
  49. ^ Doherty, Marcus W.; Manson, Neil B.; Delaney, Paul; Jelezko, Fedor; Wrachtrup, Jörg; Hollenberg, Lloyd C.L. (July 2013). "The nitrogen-vacancy colour centre in diamond". Physics Reports. 528 (1): 1–45. arXiv:1302.3288. Bibcode:2013PhR...528....1D. doi:10.1016/j.physrep.2013.02.001. S2CID 119113089.
  50. ^ Doherty, Marcus W.; Manson, Neil B.; Delaney, Paul; Jelezko, Fedor; Wrachtrup, Jörg; Hollenberg, Lloyd C. L. (2013-07-01). "The nitrogen-vacancy colour centre in diamond". Physics Reports. 528 (1): 1–45. arXiv:1302.3288. Bibcode:2013PhR...528....1D. CiteSeerX 10.1.1.743.9147. doi:10.1016/j.physrep.2013.02.001. S2CID 119113089.
  51. ^ Choi, SangKook (2012-01-01). "Mechanism for optical initialization of spin in NV". Physical Review B. 86 (4): 041202. Bibcode:2012PhRvB..86d1202C. doi:10.1103/PhysRevB.86.041202.
  52. ^ Robledo, Lucio; Bernien, Hannes; Sar, Toeno van der; Hanson, Ronald (2011-01-01). "Spin dynamics in the optical cycle of single nitrogen-vacancy centres in diamond". New Journal of Physics. 13 (2): 025013. arXiv:1010.1192. Bibcode:2011NJPh...13b5013R. doi:10.1088/1367-2630/13/2/025013. S2CID 55207459.
  53. ^ Hanson, R.; Gywat, O.; Awschalom, D. D. (2006). "Room-temperature manipulation and decoherence of a single spin in diamond" (PDF). Physical Review B. 74 (16): 161203. arXiv:quant-ph/0608233. Bibcode:2006PhRvB..74p1203H. doi:10.1103/PhysRevB.74.161203. S2CID 5055366.
  54. ^ Dutt, M. V. G.; et al. (2007). "Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond" (PDF). Science. 316 (5829): 1312–6. Bibcode:2007Sci...316.....D. doi:10.1126/science.1139831. PMID 17540898. S2CID 20697722.[permanent dead link‍]
  55. ^ Childress, L.; et al. (2006). "Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond". Science. 314 (5797): 281–5. Bibcode:2006Sci...314..281C. doi:10.1126/science.1131871. PMID 16973839. S2CID 18853275.
  56. ^ Batalov, A.; et al. (2008). "Temporal Coherence of Photons Emitted by Single Nitrogen-Vacancy Defect Centers in Diamond Using Optical Rabi-Oscillations" (PDF). Physical Review Letters. 100 (7): 077401. Bibcode:2008PhRvL.100g7401B. doi:10.1103/PhysRevLett.100.077401. hdl:11858/00-001M-0000-0011-A088-E. PMID 18352594.
  57. ^ Jelezko, F.; et al. (2004). "Observation of Coherent Oscillations in a Single Electron Spin" (PDF). Physical Review Letters. 92 (7): 076401. Bibcode:2004PhRvL..92g6401J. doi:10.1103/PhysRevLett.92.076401. PMID 14995873.[permanent dead link‍]
  58. ^ Maze, J. R.; Stanwix, P. L.; Hodges, J. S.; Hong, S.; Taylor, J. M.; Cappellaro, P.; Jiang, L.; Dutt, M. V. Gurudev; Togan, E.; Zibrov, A. S.; Yacoby, A. (October 2008). "Nanoscale magnetic sensing with an individual electronic spin in diamond". Nature. 455 (7213): 644–647. Bibcode:2008Natur.455..644M. doi:10.1038/nature07279. PMID 18833275. S2CID 136428582.
  59. ^ a b Degen, C. L.; Reinhard, F.; Cappellaro, P. (2017-07-25). "Quantum sensing". Reviews of Modern Physics. 89 (3): 035002. arXiv:1611.02427. Bibcode:2017RvMP...89c5002D. doi:10.1103/RevModPhys.89.035002. S2CID 2555443.
  60. ^ Waldherr, G.; Wang, Y.; Zaiser, S.; Jamali, M.; Schulte-Herbrüggen, T.; Abe, H.; Ohshima, T.; Isoya, J.; Du, J. F.; Neumann, P.; Wrachtrup, J. (February 2014). "Quantum error correction in a solid-state hybrid spin register". Nature. 506 (7487): 204–207. arXiv:1309.6424. Bibcode:2014Natur.506..204W. doi:10.1038/nature12919. PMID 24476818. S2CID 205237059.
  61. ^ MacQuarrie, E. R.; Gosavi, T. A.; Bhave, S. A.; Fuchs, G. D. (2015-12-14). "Continuous dynamical decoupling of a single diamond nitrogen-vacancy center spin with a mechanical resonator". Physical Review B. 92 (22): 224419. arXiv:1510.01194. Bibcode:2015PhRvB..92v4419M. doi:10.1103/PhysRevB.92.224419. S2CID 53320913.
  62. ^ Sasaki, Kento; Monnai, Yasuaki; Saijo, Soya; Fujita, Ryushiro; Watanabe, Hideyuki; Ishi-Hayase, Junko; Itoh, Kohei M.; Abe, Eisuke (2016-05-01). "Broadband, large-area microwave antenna for optically detected magnetic resonance of nitrogen-vacancy centers in diamond". Review of Scientific Instruments. 87 (5): 053904. arXiv:1605.04627. doi:10.1063/1.4952418. PMID 27250439. S2CID 25096136.
  63. ^ Bürgler, B.; Sjolander, T. F.; Brinza, O.; Tallaire, A.; Achard, J.; Maletinsky, P. (2023-06-10). "All-optical nuclear quantum sensing using nitrogen-vacancy centers in diamond". npj Quantum Information. 9 (1): 1–7. doi:10.1038/s41534-023-00724-6. ISSN 2056-6387. PMC 11041803. PMID 38665257.
  64. ^ Jarmola, A.; Fescenko, I.; Acosta, V. M.; Doherty, M. W.; Fatemi, F. K.; Ivanov, T.; Budker, D.; Malinovsky, V. S. (2020-04-28). "Robust optical readout and characterization of nuclear spin transitions in nitrogen-vacancy ensembles in diamond". Physical Review Research. 2 (2). arXiv:2001.00109. doi:10.1103/physrevresearch.2.023094. ISSN 2643-1564.
  65. ^ Teissier, J.; Barfuss, A.; Appel, P.; Neu, E.; Maletinsky, P. (2014-07-10). "Strain Coupling of a Nitrogen-Vacancy Center Spin to a Diamond Mechanical Oscillator". Physical Review Letters. 113 (2): 020503. arXiv:1403.3405. Bibcode:2014PhRvL.113b0503T. doi:10.1103/PhysRevLett.113.020503. PMID 25062153. S2CID 119244679.
  66. ^ Grotz, Bernhard; Hauf, Moritz V.; Dankerl, Markus; Naydenov, Boris; Pezzagna, Sébastien; Meijer, Jan; Jelezko, Fedor; Wrachtrup, Jörg; Stutzmann, Martin; Reinhard, Friedemann; Garrido, Jose A. (2012). "Charge state manipulation of qubits in diamond". Nature Communications. 3 (1): 729. Bibcode:2012NatCo...3..729G. doi:10.1038/ncomms1729. PMC 3316888. PMID 22395620.
  67. ^ Neethirajan, Jeffrey Neethi; Hache, Toni; Paone, Domenico; Pinto, Dinesh; Denisenko, Andrej; Stöhr, Rainer; Udvarhelyi, Péter; Pershin, Anton; Gali, Adam; Wrachtrup, Joerg; Kern, Klaus; Singha, Aparajita (2023-04-12). "Controlled Surface Modification to Revive Shallow NV – Centers". Nano Letters. 23 (7): 2563–2569. doi:10.1021/acs.nanolett.2c04733. ISSN 1530-6984. PMC 10103335. PMID 36927005.
  68. ^ Ji, Peng; Dutt, M. V. Gurudev (2016-07-05). "Charge state dynamics of the nitrogen vacancy center in diamond under 1064-nm laser excitation". Physical Review B. 94 (2). arXiv:1603.08066. doi:10.1103/PhysRevB.94.024101. ISSN 2469-9950.
  69. ^ a b Laraoui, Abdelghani; Aycock-Rizzo, Halley; Gao, Yang; Lu, Xi; Riedo, Elisa; Meriles, Carlos A. (2015). "Imaging thermal conductivity with nanoscale resolution using a scanning spin probe". Nature Communications. 6 (8954): 8954. arXiv:1511.06916. Bibcode:2015NatCo...6.8954L. doi:10.1038/ncomms9954. PMC 4673876. PMID 26584676.
  70. ^ Maze, J. R.; Stanwix, P. L.; Hodges, J. S.; Hong, S.; Taylor, J. M.; Cappellaro, P.; Jiang, L.; Dutt, M. V. G.; Togan, E.; Zibrov, A. S.; Yacoby, A.; Walsworth, R. L.; Lukin, M. D. (2008). "Nanoscale magnetic sensing with an individual electronic spin in diamond" (PDF). Nature. 455 (7213): 644–647. Bibcode:2008Natur.455..644M. doi:10.1038/nature07279. PMID 18833275. S2CID 136428582. Archived from the original (PDF) on 2016-03-07. Retrieved 2015-08-29.
  71. ^ Dolde, F.; Fedder, H.; Doherty, M. W.; Nöbauer, T.; Rempp, F.; Balasubramanian, G.; Wolf, T.; Reinhard, F.; Hollenberg, L. C. L.; Jelezko, F.; Wrachtrup, J. (2011). "Electric-field sensing using single diamond spins". Nature Physics. 7 (6): 459. arXiv:1103.3432. Bibcode:2011NatPh...7..459D. doi:10.1038/nphys1969. hdl:11858/00-001M-0000-0027-768E-1. S2CID 119287960.
  72. ^ Dovzhenko, Y.; Casola, F.; Schlotter, S.; Zhou, T. X.; Büttner, F.; Walsworth, R. L.; Beach, G. S. D.; Yacoby, A. (2018-07-13). "Magnetostatic twists in room-temperature skyrmions explored by nitrogen-vacancy center spin texture reconstruction". Nature Communications. 9 (1): 2712. Bibcode:2018NatCo...9.2712D. doi:10.1038/s41467-018-05158-9. ISSN 2041-1723. PMC 6045603. PMID 30006532.
  73. ^ Jenkins, Alec; Baumann, Susanne; Zhou, Haoxin; Meynell, Simon A.; Daipeng, Yang; Watanabe, Kenji; Taniguchi, Takashi; Lucas, Andrew; Young, Andrea F.; Bleszynski Jayich, Ania C. (2022-08-17). "Imaging the Breakdown of Ohmic Transport in Graphene". Physical Review Letters. 129 (8): 087701. arXiv:2002.05065. Bibcode:2022PhRvL.129h7701J. doi:10.1103/PhysRevLett.129.087701. PMID 36053708. S2CID 211082922.
  74. ^ Scheidegger, P. J.; Diesch, S.; Palm, M. L.; Degen, C. L. (2022-05-30). "Scanning nitrogen-vacancy magnetometry down to 350 mK". Applied Physics Letters. 120 (22). arXiv:2203.15527. Bibcode:2022ApPhL.120v4001S. doi:10.1063/5.0093548. ISSN 0003-6951. S2CID 249209788.
  75. ^ Stefan, Lucio; Tan, Anthony K.C.; Vindolet, Baptiste; Högen, Michael; Thian, Dickson; Tan, Hang Khume; Rondin, Loïc; Knowles, Helena S.; Roch, Jean-François; Soumyanarayanan, Anjan; Atatüre, Mete (2021-07-22). "Multiangle Reconstruction of Domain Morphology with All-Optical Diamond Magnetometry". Physical Review Applied. 16 (1): 014054. arXiv:2101.10331. Bibcode:2021PhRvP..16a4054S. doi:10.1103/PhysRevApplied.16.014054. S2CID 231709827.
  76. ^ Zhou, Tony X.; Stöhr, Rainer J.; Yacoby, Amir (2017-10-16). "Scanning diamond NV center probes compatible with conventional AFM technology". Applied Physics Letters. 111 (16). arXiv:1706.09793. Bibcode:2017ApPhL.111p3106Z. doi:10.1063/1.4995813. ISSN 0003-6951. S2CID 4931477.
  77. ^ Grazioso, F.; Patton, B. R.; Delaney, P.; Markham, M. L.; Twitchen, D. J.; Smith, J. M. (2013). "Measurement of the full stress tensor in a crystal using photoluminescence from point defects: The example of nitrogen vacancy centers in diamond". Applied Physics Letters. 103 (10): 101905. arXiv:1110.3658. Bibcode:2013ApPhL.103j1905G. doi:10.1063/1.4819834. S2CID 119233985.
  78. ^ Shao, Linbo; Zhang, Mian; Markham, Matthew; Edmonds, Andrew; Loncar, Marko (15 December 2016). "Diamond Radio Receiver: Nitrogen-Vacancy Centers as Fluorescent Transducers of Microwave Signals". Physical Review Applied. 6 (6): 064008. Bibcode:2016PhRvP...6f4008S. doi:10.1103/PhysRevApplied.6.064008. S2CID 24851439.
  79. ^ Chang, Y.-R.; et al. (2008). "Mass production and dynamic imaging of fluorescent nanodiamonds" (PDF). Nature Nanotechnology. 3 (5): 284–8. doi:10.1038/nnano.2008.99. PMID 18654525. Archived from the original (PDF) on 2016-03-04. Retrieved 2013-03-04.
  80. ^ Nunn, Nicholas; Torelli, Marco D.; Ajoy, Ashok; Smirnov, Alex I.; Shenderova, O. (2022-03-01). "Beauty beyond the Eye: Color Centers in Diamond Particles for Imaging and Quantum Sensing Applications". Reviews and Advances in Chemistry. 12 (1): 1–21. doi:10.1134/S2634827622010044. ISSN 2634-8284. S2CID 248422954.
  81. ^ Chang, Huan-Cheng; Hsiao, Wesley Wei-Wen; Su, Meng-Chih (12 November 2018). Fluorescent Nanodiamonds (1 ed.). Wiley. pp. 93–111. ISBN 9781119477082.
  82. ^ Chang, Yi-Ren; Lee, Hsu-Yang; Chen, Kowa; Chang, Chun-Chieh; Tsai, Dung-Sheng; Fu, Chi-Cheng; Lim, Tsong-Shin; Tzeng, Yan-Kai; Fang, Chia-Yi; Han, Chau-Chung; Chang, Huan-Cheng; Fann, Wunshain (May 2008). "Mass Production and Dynamic Imaging of Fluorescent Nanodiamonds". Nature Nanotechnology. 3 (5): 284–288. doi:10.1038/nnano.2008.99. PMID 18654525.
  83. ^ Aharonovich, I.; Greentree, A. D.; Prawer, S. (2011). "Diamond photonics". Nature Photonics. 5 (7): 397. Bibcode:2011NaPho...5..397A. doi:10.1038/nphoton.2011.54.
  84. ^ Jeske, Jan; Lau, Desmond W. M.; Vidal, Xavier; McGuinness, Liam P.; Reineck, Philipp; Johnson, Brett C.; Doherty, Marcus W.; McCallum, Jeffrey C.; Onoda, Shinobu; Jelezko, Fedor; Ohshima, Takeshi; Volz, Thomas; Cole, Jared H.; Gibson, Brant C.; Greentree, Andrew D. (2017). "Stimulated emission from nitrogen-vacancy centres in diamond". Nature Communications. 8: 14000. arXiv:1602.07418. Bibcode:2017NatCo...814000J. doi:10.1038/ncomms14000. PMC 5290152. PMID 28128228.
  85. ^ Breeze, Jonathan D.; Sathian, Juna; Salvadori, Enrico; Alford, Neil McN; Kay, Christopher W. M. (2018-03-21). "Continuous-wave room-temperature diamond maser". Nature. 555 (7697): 493–496. arXiv:1710.07726. Bibcode:2018Natur.555..493B. doi:10.1038/nature25970. PMID 29565362. S2CID 588265.
  86. ^ Liu, Ren-Bao (22 March 2018). "A diamond age of masers". Nature. 555 (7697): 447–449. Bibcode:2018Natur.555..447L. doi:10.1038/d41586-018-03215-3. PMID 29565370. S2CID 4143597.
  87. ^ Bar-Gill, N.; Pham, L.M.; Jarmola, A.; Budker, D.; Walsworth, R.L. (2012). "Solid-state electronic spin coherence time approaching one second". Nature Communications. 4: 1743. arXiv:1211.7094. Bibcode:2013NatCo...4.1743B. doi:10.1038/ncomms2771. PMID 23612284. S2CID 964488.
  88. ^ Mamin, H. J.; Kim, M.; Sherwood, M. H.; Rettner, C. T.; Ohno, K.; Awschalom, D. D.; Rugar, D. (2013). "Nanoscale Nuclear Magnetic Resonance with a Nitrogen-Vacancy Spin Sensor". Science. 339 (6119): 557–560. Bibcode:2013Sci...339..557M. doi:10.1126/science.1231540. PMID 23372008. S2CID 206545959.
  89. ^ Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.; Schouten, R.N.; Abellán, C.; Amaya, W.; Pruneri, V.; Mitchell, M.W.; Markham, M.; Twitchen, D.J.; Elkouss, D.; Wehner, S.; Taminiau, T.H.; Hanson, R. (2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041. S2CID 205246446.
  90. ^ Atatüre, Mete; Englund, Dirk; Vamivakas, Nick; Lee, Sang-Yun; Wrachtrup, Joerg (2018). "Material platforms for spin-based photonic quantum technologies". Nature Reviews Materials. 3 (5): 38–51. Bibcode:2018NatRM...3...38A. doi:10.1038/s41578-018-0008-9. S2CID 139734402.
  91. ^ Radko, Ilya P.; Boll, Mads; Israelsen, Niels M.; Raatz, Nicole; Meijer, Jan; Jelezko, Fedor; Andersen, Ulrik L.; Huck, Alexander (2016). "Determining the internal quantum efficiency of shallow-implanted nitrogen-vacancy defects in bulk diamond" (PDF). Optics Express. 24 (24): 27715–27725. Bibcode:2016OExpr..2427715R. doi:10.1364/OE.24.027715. PMID 27906340.
  92. ^ Albrecht, R.; Bommer, A.; Deutsch, C.; Reichel, J.; Becher, C. (2013). "Coupling of a Single Nitrogen-Vacancy Center in Diamond to a Fiber-Based Microcavity". Physical Review Letters. 110 (24): 243602. arXiv:1303.7418. Bibcode:2013PhRvL.110x3602A. doi:10.1103/physrevlett.110.243602. PMID 25165921. S2CID 27859868.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Nitrogen-vacancy_center&oldid=1262036139"