Schulze method

The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential Dropping (SSD), Cloneproof Schwartz Sequential Dropping (CSSD), Beatpath Method, Beatpath Winner, Path Voting, and Path Winner.

If there is a candidate who is preferred pairwise over the other candidates, when compared in turn with each of the others, the Schulze method guarantees that candidate will win. Because of this property, the Schulze method is (by definition) a Condorcet method.

Currently, the Schulze method is the most wide-spread Condorcet method (list). The Schulze method is used by several organizations including Wikimedia, Debian, Gentoo, and Software in the Public Interest.

Many different heuristics for computing the Schulze method have been proposed. The most important heuristics are the path heuristic and the Schwartz set heuristic that are described below. All heuristics find the same winner and only differ in the details of the computational procedure to determine this winner.

The path heuristic

Example Schulze method ballot

Under the Schulze method (as well as under other preferential single-winner election methods), each ballot contains a complete list of all candidates and the individual voter ranks this list in order of preference. Under a common ballot layout (as shown in the image to the right), ascending numbers are used, whereby the voter places a '1' beside the most preferred candidate, a '2' beside the second-most preferred, and so forth.

Each voter may ...

• ... give the same preference to more than one candidate. This indicates that this voter is indifferent between these candidates.

• ... skip preferences. However, skipping preferences has no impact on the result of the elections, since only the order, in which the candidates are ranked, matters and not the absolute numbers of the preferences.

• ... keep candidates unranked. When a voter doesn't rank all candidates, then this is interpreted as if this voter:

... (1) strictly prefers all ranked to all unranked candidates, and

... (2) is indifferent between all unranked candidates.

The basic idea of the path heuristic for the Schulze method is the concept of indirect defeats, the so-called paths.

If candidate C(1) pairwise beats candidate C(2), candidate C(2) pairwise beats candidate C(3), candidate C(3) pairwise beats candidate C(4), ..., and C(n-1) pairwise beats candidate C(n), then we say that there is a path from candidate C(1) to candidate C(n). The strength of the path C(1),...,C(n) is the weakest pairwise defeat in this sequence.

In other words:

• Suppose d[V,W] is the number of voters who strictly prefer candidate V to candidate W.

• A path is a sequence of candidates C(1),...,C(n) with d[C(i),C(i+1)] > d[C(i+1),C(i)] for all i = 1,...,(n-1).

• The strength of the path C(1),...,C(n) is the minimum of all d[C(i),C(i+1)] for i = 1,...,(n-1).

The strength of the strongest path from candidate A to candidate B is the maximum of the strengths of all paths from candidate A to candidate B.

Candidate A pairwise beats candidate B indirectly if either

• the strength of the strongest path from candidate A to candidate B is stronger than the strength of the strongest path from candidate B to candidate A or

• there is a path from candidate A to candidate B and no path from candidate B to candidate A.

Indirect defeats are transitive. That means: If candidate A pairwise beats candidate B indirectly and candidate B pairwise beats candidate C indirectly, then also candidate A pairwise beats candidate C indirectly. Therefore, no tie-breaker is needed for indirect defeats.

Procedure

Suppose d[V,W] is the number of voters who strictly prefer candidate V to candidate W.

A path from candidate X to candidate Y of strength p is a sequence of candidates C(1),...,C(n) with the following properties:

1. C(1) = X and C(n) = Y.
2. For all i = 1,...,(n-1): d[C(i),C(i+1)] > d[C(i+1),C(i)].
3. For all i = 1,...,(n-1): d[C(i),C(i+1)] ≥ p.

p[A,B], the strength of the strongest path from candidate A to candidate B, is the maximum value such that there is a path from candidate A to candidate B of that strength. If there is no path from candidate A to candidate B at all, then p[A,B] : = 0.

Candidate D is better than candidate E if and only if p[D,E] > p[E,D].

Candidate D is a potential winner if and only if p[D,E] ≥ p[E,D] for every other candidate E.

Remark

It is possible to prove that p[X,Y] > p[Y,X] and p[Y,Z] > p[Z,Y] together imply p[X,Z] > p[Z,X] . Therefore, it is guaranteed (1) that the above definition of "better" really defines a transitive relation and (2) that there is always at least one candidate D with p[D,E] ≥ p[E,D] for every other candidate E.

Example

Example (45 voters; 5 candidates):

5 ACBED (that is, 5 voters have order of preference: A > C > B > E > D)

5 ADECB

8 BEDAC

3 CABED

7 CAEBD

2 CBADE

7 DCEBA

8 EBADC

The matrix of pairwise defeats looks as follows:

	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

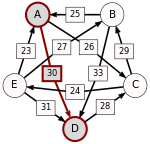
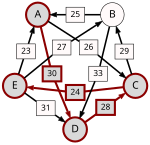
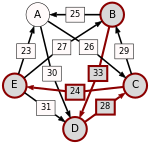
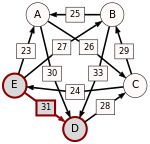
The graph of pairwise defeats looks as follows:

The strength of a path is the strength of its weakest link. For each pair of candidates X and Y, the following table lists the strongest path from candidate X to candidate Y. The critical defeats of the strongest paths are underlined.

The strongest paths are:

	... to A	... to B	... to C	... to D	... to E
from A ...		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E	from A ...
from B ...	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E	from B ...
from C ...	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E	from C ...
from D ...	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E	from D ...
from E ...	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D		from E ...
	... to A	... to B	... to C	... to D	... to E

The strengths of the strongest paths are:

	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

Candidate E is a potential winner, because p[E,X] ≥ p[X,E] for every other candidate X.

As 25 = p[E,A] > p[A,E] = 24, candidate E is better than candidate A.

As 28 = p[E,B] > p[B,E] = 24, candidate E is better than candidate B.

As 28 = p[E,C] > p[C,E] = 24, candidate E is better than candidate C.

As 31 = p[E,D] > p[D,E] = 24, candidate E is better than candidate D.

As 28 = p[A,B] > p[B,A] = 25, candidate A is better than candidate B.

As 28 = p[A,C] > p[C,A] = 25, candidate A is better than candidate C.

As 30 = p[A,D] > p[D,A] = 25, candidate A is better than candidate D.

As 29 = p[C,B] > p[B,C] = 28, candidate C is better than candidate B.

As 29 = p[C,D] > p[D,C] = 28, candidate C is better than candidate D.

As 33 = p[B,D] > p[D,B] = 28, candidate B is better than candidate D.

Therefore, the Schulze ranking is E > A > C > B > D.

Implementation

Suppose C is the number of candidates. Then the strengths of the strongest paths can be calculated with the Floyd–Warshall algorithm . The following Pascal-like pseudocode illustrates the determination of such a path.

Input: d[i,j] is the number of voters who strictly prefer candidate i to candidate j.

Output: p[i,j] is the strength of the strongest path from candidate i to candidate j.

for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         if ( d[i,j] > d[j,i] ) then
         begin
            p[i,j] : = d[i,j]
         end
         else
         begin
            p[i,j] : = 0
         end
      end
   end
end

for i : = 1 to C
begin
   for j : = 1 to C
   begin
      if ( i ≠ j ) then
      begin
         for k : = 1 to C
         begin
            if ( i ≠ k ) then
            begin   
               if ( j ≠ k ) then
               begin
                  p[j,k] : = max ( p[j,k], min ( p[j,i], p[i,k] ) )
               end
            end
         end
      end
   end
end

The Schwartz set heuristic

Procedure

The Schwartz set heuristic for the Schulze method is an iterative heuristic.

At each stage, we proceed as follows:

1. For each pair of undropped candidates X and Y: If there is a directed path of undropped links from candidate X to candidate Y, then we write "X → Y"; otherwise we write "not X → Y".
2. For each pair of undropped candidates V and W: If "V → W" and "not W → V", then candidate W is dropped and all links, that start or end in candidate W, are dropped.
3. The weakest undropped link is dropped. If several undropped links tie as weakest, all of them are dropped.

The procedure ends when all links have been dropped. The winners are the undropped candidates.

Example

Example (30 voters; 4 candidates):

3 ACDB

9 BACD

8 CDAB

5 DABC

5 DBCA

The matrix of pairwise defeats looks as follows:

	d[*,A]	d[*,B]	d[*,C]	d[*,D]
d[A,*]		16	17	12
d[B,*]	14		19	9
d[C,*]	13	11		20
d[D,*]	18	21	10

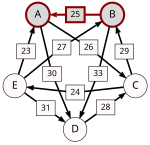
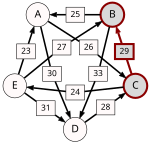
The graph of pairwise defeats looks as follows:

We get: "A → B", "A → C", "A → D", "B → A", "B → C", "B → D", "C → A", "C → B", "C → D", "D → A", "D → B", and "D → C".

As there is no pair of candidates V and W with "V → W" and "not W → V", no candidate can be dropped.

The weakest undropped link (A:B=16:14) is dropped.

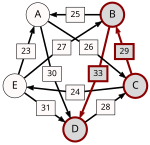
Thus, we get:

We get: "A → B", "A → C", "A → D", "B → A", "B → C", "B → D", "C → A", "C → B", "C → D", "D → A", "D → B", and "D → C".

As there is no pair of candidates V and W with "V → W" and "not W → V", no candidate can be dropped.

The weakest undropped link (A:C=17:13) is dropped.

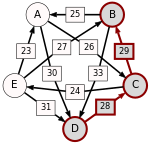
Thus, we get:

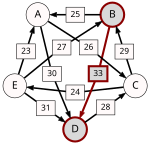
We get: "not A → B", "not A → C", "not A → D", "B → A", "B → C", "B → D", "C → A", "C → B", "C → D", "D → A", "D → B", and "D → C".

As "B → A" and "not A → B", candidate A is dropped and all links, that start or end in candidate A, are dropped.

Thus, we get:

The weakest undropped link (B:C=19:11) is dropped.

Thus, we get:

We get: "not B → C", "not B → D", "C → B", "C → D", "D → B", and "not D → C".

As "C → B" and "not B → C", candidate B is dropped and all links, that start or end in candidate B, are dropped; as "C → D" and "not D → C", candidate D is dropped and all links, that start or end in candidate D, are dropped.

As candidate C is the unique undropped candidate, candidate C is the unique winner.

Satisfied and failed criteria

Satisfied criteria

The Schulze method satisfies the following criteria:

• Unrestricted domain
• Non-imposition (a.k.a. citizen sovereignty)
• Non-dictatorship
• Pareto criterion
• Monotonicity criterion
• Majority criterion
• Majority loser criterion
• Condorcet criterion
• Condorcet loser criterion
• Schwartz criterion
• Smith criterion
• Independence of Smith-dominated alternatives
• Mutual majority criterion
• Independence of clones
• Reversal symmetry
• Mono-append
• Mono-add-plump
• Resolvability criterion
• Polynomial runtime

If winning votes is used as the definition of defeat strength, it also satisfies:

• Woodall's plurality criterion

If margins as defeat strength is used, it also satisfies:

• Symmetric-completion

Failed criteria

The Schulze method violates the following criteria:

• All criteria that are incompatible with the Condorcet criterion (e.g. independence of irrelevant alternatives, participation , consistency, invulnerability to compromising, invulnerability to burying, later-no-harm)

Independence of irrelevant alternatives

The Schulze method fails independence of irrelevant alternatives. However, the method adheres to a less strict property that is sometimes called independence of Smith-dominated alternatives. It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set. Local IIA implies the Condorcet criterion.

Comparison with other preferential single-winner election methods

The following table compares the Schulze method with other preferential single-winner election methods:

	Monotonic	Condorcet	Condorcet loser	Majority	Majority loser	Mutual majority	Smith	ISDA	Clone independence	Reversal symmetry	Polynomial time	Participation, Consistency
Schulze	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No
Ranked Pairs	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No
Kemeny-Young	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	No	No
MiniMax	Yes	Yes	No	Yes	No	No	No	No	No	No	Yes	No
Nanson	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	Yes	Yes	No
Baldwin	No	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	Yes	No
Instant-runoff voting	No	No	Yes	Yes	Yes	Yes	No	No	Yes	No	Yes	No
Coombs	No	No	Yes	Yes	Yes	Yes	No	No	No	No	Yes	No
Contingent voting	No	No	Yes	Yes	Yes	No	No	No	No	No	Yes	No
Sri Lankan contingent voting	No	No	No	Yes	No	No	No	No	No	No	Yes	No
Supplementary voting	No	No	No	Yes	No	No	No	No	No	No	Yes	No
Borda	Yes	No	Yes	No	Yes	No	No	No	No	Yes	Yes	Yes
Bucklin	Yes	No	No	Yes	Yes	Yes	No	No	No	No	Yes	No
Plurality	Yes	No	No	Yes	No	No	No	No	No	No	Yes	Yes
Anti-plurality	Yes	No	No	No	Yes	No	No	No	No	No	Yes	Yes

This is the main difference between the Schulze method and the Ranked Pairs method:

Suppose the MinMax score of a set X of candidates is the strength of the strongest pairwise win of a candidate A ∉ X against a candidate B ∈ X. Then the Schulze method, but not the Ranked Pairs method, guarantees that the winner is always a candidate of the set with minimum MinMax score . So, in some sense, the Schulze method minimizes the strongest pairwise win that has to be overturned when determining the winner.

History of the Schulze method

The Schulze method was developed by Markus Schulze in 1997. The first times that the Schulze method was discussed in a public mailing list were in 1998 and in 2000 . In the following years, the Schulze method has been adopted e.g. by Software in the Public Interest (2003) , Debian (2003) , Gentoo (2005), TopCoder (2005), Sender Policy Framework (2005), and the French Wikipedia section (2005). The first books on the Schulze method were written by Tideman (2006) and by Stahl and Johnson (2007). In the then following years, the Schulze method has been adopted e.g. by Wikimedia (2008) and KDE (2008).

Use of the Schulze method

sample ballot for Wikimedia's Board of Trustees elections

The Schulze method is not currently used in government elections. However, it is starting to receive support in some public organizations. Organizations which currently use the Schulze method are:

• Annodex Association
• Blitzed
• BoardGameGeek
• Codex Alpe Adria
• College of Marine Science
• Computer Science Departmental Society for York University (HackSoc)
• County Highpointers
• Debian
• Digital Freedom in Education and Youth
• EnMasse Forums
• EuroBillTracker
• European Democratic Education Conference
• Fair Trade Northwest
• Free Hardware Foundation of Italy
• Free Software Foundation Europe (FSFE)
• Free Software Foundation Latin America (FSFLA)
• Gentoo Foundation
• GNU Privacy Guard (GnuPG)
• Graduate Student Organization at the State University of New York: Computer Science (GSOCS)
• Haskell
• Kanawha Valley Scrabble Club
• KDE e.V.
• Kingman Hall
• Knight Foundation
• Kumoricon
• League of Professional System Administrators (LOPSA)
• Libre-Entreprise
• Lumiera/Cinelerra
• Mason Apollonic Society
• Mathematical Knowledge Management Interest Group (MKM-IG)
• Metalab
• Music Television (MTV)
• netznetz
• North Shore Cyclists (NSC)
• OpenCouchSurfing
• Park Alumni Society (PAS)
• Pitcher Plant of the Month
• Pittsburgh Ultimate
• RPMrepo
• Sender Policy Framework (SPF)
• Software in the Public Interest (SPI)
• Students for Free Culture
• TopCoder
• Wikimedia Foundation
• Wikipedia in French
• Wikipedia in Hebrew
• Wikipedia in Hungarian
• Wikipedia in Russian
• Wikipedia in Spanish

Notes

Schulze1: Markus Schulze, A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method

External links

Note that these sources may refer to the Schulze method as CSSD, SSD, beatpath, path winner, etc.

General

• Proposed Statutory Rules for the Schulze Single-Winner Election Method by Markus Schulze
• A New Monotonic and Clone-Independent Single-Winner Election Method by Markus Schulze (mirrors: [1] [2])
• A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method by Markus Schulze
• Free Riding and Vote Management under Proportional Representation by the Single Transferable Vote by Markus Schulze
• Implementing the Schulze STV Method by Markus Schulze
• A New MMP Method by Markus Schulze
• A New MMP Method (Part 2) by Markus Schulze

Tutorials

• Spieltheorie Template:De icon by Bernhard Nebel
• Schulze-Methode Template:De icon by the University of Stuttgart

Advocacy

• Election Methods Resource by Blake Cretney
• Voting Methods Survey by James Green-Armytage
• Descriptions of ranked-ballot voting methods by Rob LeGrand
• Accurate Democracy by Rob Loring
• Schulze beatpaths method by Warren D. Smith
• Election Methods and Criteria by Kevin Venzke
• The Debian Voting System by Jochen Voss
• election-methods: a mailing list containing technical discussions about election methods

Research papers

• A Continuous Rating Method for Preferential Voting by Rosa Camps, Xavier Mora, and Laia Saumell (mirror: [3])
• Voting Systems by Paul E. Johnson
• Test Run: Group Determination in Software Testing by James D. McCaffrey
• Distance from Consensus: a Theme and Variations by Tommi Meskanen and Hannu Nurmi
• Analyzing Political Disagreement by Tommi Meskanen and Hannu Nurmi
• Descriptions of voting systems by Warren D. Smith
• Election Systems by Peter A. Taylor
• Personalisierung der Verhältniswahl durch Varianten der Single Transferable Vote Template:De icon by Martin Wilke
• Objective Measures of Preferential Ballot Voting Systems by Barry Wright
• Approaches to Constructing a Stratified Merged Knowledge Base by Anbu Yue, Weiru Liu, and Anthony Hunter

Books

• Saul Stahl and Paul E. Johnson (2007), Understanding Modern Mathematics, Sudbury: Jones and Bartlett Publishers, ISBN 0-7637-3401-2
• Nicolaus Tideman (2006), Collective Decisions and Voting: The Potential for Public Choice, Burlington: Ashgate, ISBN 0-7546-4717-X

Software

• Voting Software Project by Blake Cretney
• Condorcet with Dual Dropping Perl Scripts by Mathew Goldstein
• Condorcet Voting Calculator by Eric Gorr
• Selectricity and RubyVote by Benjamin Mako Hill [4] [5]
• Java implementation of the Schulze method by Thomas Hirsch
• Electowidget by Rob Lanphier
• Votator.com by Louis Philippe Lessard [6]
• Haskell Condorcet Module by Evan Martin
• Condorcet Internet Voting Service (CIVS) by Andrew Myers
• BetterPolls.com by Brian Olson
• OpenSTV by Jeffrey O'Neill

Legislative projects

• Arizonans for Condorcet Ranked Voting [7] [8] [9] [10]
• Schulze Method Phoenix