Talk:Linear time-invariant system
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
This article links to one or more target anchors that no longer exist.
Please help fix the broken anchors. You can remove this template after fixing the problems. | Reporting errors |
Example
[edit]Need to put an example for the discrete time case to make things a little clearer.
- I say this side focuses too much on continuous time (CT). The concept of LTI should be explained independent of whether or not the time is continuous. For example, it is difficult to link from a side which discusses digital signal processing algorithms to this LTI side, because it only talks about CT signal processing. Also, LSI (Linear Shift Invariance), which means basically the same thing, must be mentioned. Faust o 20:25, 23 January 2006 (UTC)
i think there is a lot more that can be done to make this clearer.
[edit]but i'm glad the article is there. this should be written so that it can be understood by someone who doesn't already understand it. to begin with, i think there needs to be a better introduction as to what is. what are the fundamental properties of this LTI operator ? first exactly what does it mean for to be linear (the additive superposition property) and then what does it mean for to be time-invariant. then from that derive the more general superposition property, then introduce the dirac delta impulse as an input and define the output of to be the impulse response. since the article is LTI, there is no need to introduce . all that does is obfuscate.
Mark, i hope you don't mind if i whack at this a bit in the near future. i gotta figure out how to draw a png image and upload it. r b-j 04:53, 28 Apr 2005 (UTC)
- I disagree. I think should be there, as it shows how much simpler things become when translation invariance is imposed. I think you can represent any linear system with , but I'm not 100% sure. Certainly any nice system. - Jpkotta 06:40, 12 February 2006 (UTC)
- you're correct when you say that "you can represent any linear system with ", but that is more general than LTI and unnecessarily complicated. that expression includes Linear, time-variant systems also. perhaps the article should be just "Linear systems" and deal with both time-variant and time-invariant. r b-j 07:25, 14 February 2006 (UTC)
Representation
[edit]It appears that it is assumed that the LTI linear system can be represented by a convolution. However, in Zemanian's book on distributions a result due to Schwatrz and its proof are presented. The result has to do with sufficient conditions under which an LTI transformation can be represented by a convolution. I guess that continuity of the LTI transformation is one of the conditions. The result appears to be quite deep. Some other proofs in the literature may not be real proofs. This result is not as simple as one might think.
Yaacov
I deleted the word "integral" from my comment. The convolution of didtributions has a definition that does not appear to rely on integration.
Yaacov
I added: "Some other proofs in the literature may not be real proofs. This result is not as simple as one might think."
Yaacov
Notation
[edit]Is the bb font at all common for an operator? I've never seen that before, and I think bb font should be reserved for sets like the reals and complexes. A clumsy but informative notation that one of my professors uses is this:
,
where is the operator, to is the output variable, and ti is the input variable. To say that a system is TI,
.
I'm not sure if it's a good idea to use it here though... -- Jpkotta 06:49, 12 February 2006 (UTC)
Discete time
[edit]Should discrete time be folded in with continuous time, or should there be two halves of the article?
By folded, I mean:
- basics
- what it means to be LTI in C.T.
- what it means to be LTI in D.T.
- transforms
- laplace
- z
By two halves, I mean
- C.T.
- what it means to be LTI
- Laplace
- D.T.
- what it means to be LTI
- z transform
I vote for the two halves option, because then it would be easier to split into two articles in the future. -- Jpkotta 06:46, 12 February 2006 (UTC)
I made a big update to the article, and most of it was to add a "mirror image" of the CT stuff for DT. There is a bit more to go, but it's almost done. -- Jpkotta 22:25, 21 April 2006 (UTC)
Comparison with Green function
[edit]This page has the equation
which looks an awful lot like the application of a Green function
however this page doesn't even mention Green functions. Can someone explan when the two approaches can be applied? (My hunch right now is that Green functions can be used for linear systems that are not necessarily time-invariant.) —Ben FrantzDale 03:24, 17 November 2006 (UTC)
- Yes, a Green's function is essentially an impulse response. Different fields have developed different terms for these things. But the Green's function is also more general, as you note, than is needed for time-invariant systems; as is that h(t1,t2) integral. Dicklyon 06:14, 17 November 2006 (UTC)
Discrete example confusion
[edit]The first example starts out describing the delay operator then describes the difference operator. 203.173.167.211 23:03, 3 February 2007 (UTC)
- I fixed it. And changed z to inverse z for the delay operator. I'm not sure where that came from or whether I've left some discrepancy. Dicklyon 01:30, 4 February 2007 (UTC)
Problem with linearity
[edit]Generally, it is not true that for a linear operator L (such that ), that
over arbitrary index sets (i.e. infinite sums). This is used heavily in LTI analysis.
The result does not follow from induction. So why should it be true for linear systems? I think linearity itself is not strong enough a condition to warrant the infinite-sum result. Are there deeper maths behind systems analysis that provide this result? (For example, restriction of linear systems to duals of certain maps is a sufficiently strong condition to imply this result.) 18.243.2.126 (talk) 01:42, 13 February 2008 (UTC)
- Are you saying it's not true? Or that you don't know how to prove it? Do you have a counter-example? Dicklyon (talk) 05:07, 13 February 2008 (UTC)
- It is plainly not true, if linearity is the only condition being imposed (the constant signal x[n] = 1 is linearly independent from the unit impulses and all their shifts -- while this is not the case if you allow infinite sums); I have yet to construct a viable time-invariant counterexample; time-invariant functionals tend to be a lot more restrictive. For example, any time invariant system which only outputs constant signals is identically the zero system. 18.243.2.126 (talk) 00:21, 19 February 2008 (UTC)
- I'm not following you. What is the concept of "linearly independent" and how does it relate to the question at hand? Dicklyon (talk) 06:10, 19 February 2008 (UTC)
- The terminology comes from linear algebra (the wiki article explains it better than I can in a short paragraph). Note that the set of real-valued signals forms a real vector space. 18.243.2.126 (talk) 19:28, 20 February 2008 (UTC)
- I understand about linear algebra and vector spaces, but there's nothing in this article, nor in linear algebra about this concept you've brought up, so tell us why you think it's relevant. Dicklyon (talk) 20:05, 20 February 2008 (UTC)
- I see that linear independence says "In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection." This renders your above statement "while this is not the case if you allow infinite sums" somewhat meaningless. So I still don't get your point. Dicklyon (talk) 20:10, 20 February 2008 (UTC)
- In what way does it "not follow from induction"? Oli Filth(talk) 12:02, 13 February 2008 (UTC)
- Induction can prove it for all finite subsequences of the infinite index sequences, without bound, but not for the infinite sequence itself. Dicklyon (talk) 16:24, 13 February 2008 (UTC)
New footnote
[edit]I've removed the recently-added footnote, because I'm not sure what it says is relevant. The explanation of the delay operator is purely an example of "it's easier to write", as by substitution, . The differentiation explanation is irrelevant, because when using z, we're in discrete time, and so would never differentiate w.r.t. continuous time. Oli Filth(talk) 21:28, 10 April 2008 (UTC)
"any input"?
[edit]Is this nonsense?:
- "Again using the sifting property of the , we can write any input as a superposition of deltas:
- "
--Bob K (talk) 00:52, 11 June 2008 (UTC)
- Other than special cases which one would need to resort to Lebesgue measures to describe, I don't think it's nonsense. What specifically are you questioning, the maths itself, or the use of the qualifier "any"? Oli Filth(talk) 08:05, 11 June 2008 (UTC)
- It sounds like we are saying that delta functions are a basis set (like sinusoids) for representing signals.
- Anyhow, I think the "proof" was redundant at best. At worst, it was circular logic, because it uses this formula:
- which is a special case of this one:
| (Eq.1) |
- to derive this one:
- which is the same as Eq.1.
- --Bob K (talk) 13:24, 11 June 2008 (UTC)
- Just for the record, I think what someone was trying to do is done correctly (but for the discrete case) at Impulse response.
- --Bob K (talk) 19:21, 13 July 2008 (UTC)
- In the discrete case, the delayed delta signals certainly are a basis set. I'm not sure about the continuous case. However, I agree that the proof was somewhat circular. Oli Filth(talk) 15:45, 11 June 2008 (UTC)
- Well besides that fact that neither of us has ever heard of using Dirac deltas as a basis set for all continuous signals, how does one make the leap from that dubious statement to this?:
- I believe it is just nonsense.
- --Bob K (talk) 18:04, 11 June 2008 (UTC)
- We know the following is true (it's the response of system x(t) to an impulse):
- and we also know that convolution is commutative. Oli Filth(talk) 18:24, 11 June 2008 (UTC)
- Those two statements of yours have nothing to do with the assertion that Dirac deltas are a basis set for all continuous signals and therefore nothing to do with my question.
- --Bob K (talk) 23:24, 11 June 2008 (UTC)
- You said "besides that fact" above. I'm not defending the material (I didn't write it); just playing devil's advocate... I feel perhaps we are talking at cross purposes! Oli Filth(talk) 23:30, 11 June 2008 (UTC)
- Out of context, the integral formula is fine. But I quoted the entire statement and asked if it makes any sense. (You said it does.) Even if you accept the idea of Dirac deltas as basis functions [I don't], how does the integral formula follow from that? The whole thing just seems silly.
- --Bob K (talk) 00:17, 12 June 2008 (UTC)
- There is no circular logic, all it uses is the sifting property.
- Consider the identity system, i.e. the system that simply returns the input, unchanged. It is clearly LTI. What is the impulse response of the identity system? How would you compute the output using a convolution? This leads directly to the above statement.
- If you accept that sinusoids are basis functions, then why can't deltas be basis functions? The Fourier transforms of the sinusoids are deltas. I can take inner products of a signal and deltas (another way to interpret the above formula) and completely specify the signal up to a set of measure zero, just as I can with sinusoids.
- Jpkotta (talk) 03:51, 6 October 2008 (UTC)
Is Overview written at the right level?
[edit]In the Overview section, this paragraph abruptly appears:
For all LTI systems, the eigenfunctions, and the basis functions of the transforms, are complex exponentials. This is, if the input to a system is the complex waveform for some complex amplitude and complex frequency , the output will be some complex constant times the input, say for some new complex amplitude . The ratio is the transfer function at frequency .
But complex amplitude and complex frequency are not really the inputs and outputs of the system. It's like saying that radios transmit and receive analytic signals. For the sake of those who don't already know the subject, wouldn't it be better to stick closer to reality than to mathematical abstractions?
--Bob K (talk) 11:32, 18 June 2008 (UTC)
- For practical (i.e. physically-realisable) systems using actual physical quantities as the "signals", then yes, it's true that the signals will be real. But I would have said that this article is about the mathematical abstraction, i.e. LTI systems in their most general form, not the subset of the theory that covers real-only signals and systems. Therefore, the complete set of eigenfunctions really is the complex exponentials. I don't think we can avoid discussing this. We could add the caveat that for real-only signals, the eigenfunctions are of the form (for real , and ), or we could explicitly explain what is meant by "complex frequency", etc. Oli Filth(talk) 12:06, 18 June 2008 (UTC)
- Those aren't eigenfunctions, since the phase can change in going through the system. You really do need complex exponentials, not just different phases of damped cosines. Dicklyon (talk) 16:38, 30 January 2009 (UTC)
- Imaginary functions do exist in real life. Every time you generate a cosine, you're actually generating two imaginary functions and summing them. By the linearity property, we handle the analysis for the two terms separately. That's not only the simplest explanation, but it's the most accurate. The imaginary analysis is not simply an abstraction; it's a useful decomposition of reality. (On a different note, it's useful to think about transmission of purely imaginary signals when describing single-sideband modulation as the baseband signal is made asymmetric after post-modulation filtering) —TedPavlic (talk) 16:26, 30 January 2009 (UTC)
- You don't think it's fair to admit that the decomposition of a cosine into a pair of complex exponentials is a decomposition of a "real" (e.g. voltage) signal into a pair of "abstract" or non-real mathematical functions? These are no longer things that can be independently sent on a wire, for example. We use them because they are the eigenfunction of continuous-time linear systems; that doesn't make them "real". Even SSB signals are real functions of time, not complex signals. In real life, all signals are real-valued, except when we use a pair of real signals, or a modulated real signal, to "represent" an otherwise non-real signal. Dicklyon (talk) 16:35, 30 January 2009 (UTC)
- It's fair, but I just think it's unnecessarily complex (pun intended? not sure) to treat the complex exponentials as abstract magic. They come right out of the definition of a (damped) sinusoids. There is a straightforward jump from real signals to decompositions of complex exponentials, and I favor that straightforward leap rather than something touchy feeley. —TedPavlic (talk) 17:15, 30 January 2009 (UTC)
- I wouldn't advocate anything touchy-feely either. If eigenfunctions are introduced, complex exponentials are unavoidable. And they're so useful that we shouldn't avoid introducing them. We need to just note that real inputs and outputs decompose into pairs of these eigenfunctions. For the intro, however, we might be able to defer that discussion and talk about linearity and time invariance without eigenfunctions, no? Dicklyon (talk) 18:46, 30 January 2009 (UTC)
- I agree. With my young students (sophomore-level engineers), I take the approach in this short document. In two pages, I try to cover all of the math they'll need to go from first principles to LTI stability, and I didn't introduce the term eigenvalue until well-into the stability discussion on the second page (and I don't give the formal definition; I justify its name using stability). The utility of having eigenvalues and eigenfunctions is obvious when just working the systems out. Naming them initially just confuses the matter (I think). Likewise, I think this article need not get deep into the abstraction. It can:
- Define linear systems (scaled sums)
- Use the definition to motivate using complex exponential functions
- Show how real signals can be composed from complex exponentials
- The order of 2 and 3 is unclear to me. However, I don't see a reason to really get deep into the algebra until at the end (or not at all?). Technically you need it in order to show that you can eigen-decompose real functions, but I think it's OK to push some of the justification for that off into some of the transform pages. —TedPavlic (talk) 19:30, 30 January 2009 (UTC)
- I agree. With my young students (sophomore-level engineers), I take the approach in this short document. In two pages, I try to cover all of the math they'll need to go from first principles to LTI stability, and I didn't introduce the term eigenvalue until well-into the stability discussion on the second page (and I don't give the formal definition; I justify its name using stability). The utility of having eigenvalues and eigenfunctions is obvious when just working the systems out. Naming them initially just confuses the matter (I think). Likewise, I think this article need not get deep into the abstraction. It can:
- That's a pretty nice develoment. But where you say "Consider functions of the form...," you do slip into complex signals in a context where previously you were talking about real-world variables. If at that point you explain that real signals can be decomposed into such things, it would be fine, but as it stands, that gap in the logic may confuse some students. Same problem a bit later when you say "We will assume that this output is made up of complex exponentials...;" the student who expects a real output may not know what to make of this. Dicklyon (talk) 04:19, 31 January 2009 (UTC)
The next paragraph after the one I quoted does mention that real signals are a subset. Perhaps it could be said in a more accessible way to more readers, but it's much better than nothing. This probably isn't the right place to explain complex frequency, but it would be an improvement if complex frequency was an internal link to an understandable article on that subject. Do we have such an article?
--Bob K (talk) 14:12, 18 June 2008 (UTC)
BTW, the article Phasor (sine waves) is an example of a more accessible approach, in my opinion, because it puts the complex representation into a context that more people can relate to. It motivates the introduction of complex amplitudes by using them to reduce a "real" problem to an elegant, easily solvable, equation:
And then it shows the additional steps to extract the "real" solution from the complex result. So from that perspective, the concept of complex amplitude is just an intermediate and temporary step in a longer process. It's actually the subset, not the superset. It is only one of the tools neded to understand all LTI systems (i.e., including realizable ones).
--Bob K (talk) 15:18, 18 June 2008 (UTC)
- But that's backwards. There are several ways to show that , and most people probably recall something like that from high school (or lower?). By the definition of an LTI system, whenever the input is the sum of two signals, we can treat each signal independently and sum the result. So we handle and then and then sum the result. It's misleading to say that we're taking the "real part" of anything here. We're not throwing anything away. We're using both the real and imaginary parts. It just so happens that since we started with all real signals, we end with all real signals. (note that there are plenty of applications where you start with complex signals and thus need complex signals out, and so it's best to leave the description as general as possible) —TedPavlic (talk) 16:32, 30 January 2009 (UTC)
math error
[edit]In the section LTI_system_theory#Time_invariance_and_linear_transformation we say:
If the linear operator is also time-invariant, then
For the choice
it follows that
But we can't make that choice, because is the variable of integration, and is a constant time offset.
The "proof" has been fudged so as to time-reverse the weighting function (as it was defined above) so that it looks like an impulse response. But an impulse response is a weighting function whose value at is the weight applied to the value of the input at time , where is the time of the desired output value. That means it is a time-reversed version of our definition of
So one way to fix the problem would be to start with the definition:
| (Eq.2) |
But the will probably confuse people. So an alternative is to show that if is defined by:
the impulse response is Then we could point out that defining as an impulse response leads to Eq.2 (and vice versa).
--Bob K (talk) 03:16, 19 June 2008 (UTC)
another math error
[edit]In section LTI_system_theory#Time_invariance_and_linear_transformation we say:
If the linear operator is also time-invariant, then
If we let
then it follows that
But we can't "let " because is the variable of integration, and is a constant offset.
--Bob K (talk) 14:06, 19 June 2008 (UTC)
Scaling from superposition
[edit]I read: "It can be shown that, given this superposition property, the scaling property follows for any rational scalar." Please correct me if I am wrong (I am not an expert), but I think it would be better to write "given this superposition property, the scaling property obviously follows for any rational scalar" (or any equivalent wording). Indeed, it seems to me that (using notations from the superposition property explanation) we simply have to take c2=0 to get the scaling property. The current wording let the reader thinks that the proof is not obvious, IMHO.--OlivierMiR (talk) 13:10, 27 January 2009 (UTC)
- The scaling property does not follow from simple additivity. For more information, see linear map. You need both additivity and homogeneity (of order 1) to call something linear. That is,
- This statement combines the two properties. It's a concise statement of two independent requirements. Note that functions can be created that are additive but not linear. —TedPavlic (talk) 16:18, 30 January 2009 (UTC)
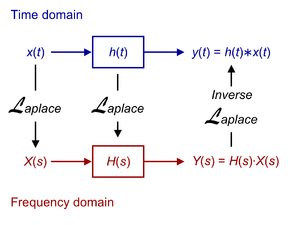
LTI.png shouldn't say "Frequency domain"
[edit]The included LTI.png image:
shows a transformation from "Time domain" to "Frequency domain." However, clearly the (or "Laplace") domain is shown, which is a generalization of the frequency domain. Either each should be changed to a or the "Frequency domain" should be changed to something like "Laplace domain" or " domain." —TedPavlic (talk) 22:55, 28 January 2009 (UTC)
- It's not so bad. The Laplace domain (complex frequencies) is probably the most commonly used frequency domain in this application. Dicklyon (talk) 00:07, 29 January 2009 (UTC)
Another problem in the picture is the ridicule notation of the convolution as . It should read: , as it is the value at of the convolution of the functions and .Madyno (talk) 19:13, 1 July 2020 (UTC)
Zero state response also discusses the analysis of linear systems, but does not make a specific restriction of the problems to time-invariant system. There is, as yet, no top-level article on Linear system theory that deals with both this and the more general case of time-variant linear systems. Is there a possible route for refactoring/merging this material? -- The Anome (talk) 02:54, 17 February 2010 (UTC)
Dubious (and misleading!) example: "ideal LPF not stable"
[edit]This paragraph:
- As an example, the ideal low-pass filter with impulse response equal to a sinc function is not BIBO stable, because the sinc function does not have a finite L1 norm. Thus, for some bounded input, the output of the ideal low-pass filter is unbounded. In particular, if the input is zero for t < 0\, and equal to a sinusoid at the cut-off frequency for t > 0\,, then the output will be unbounded for all times other than the zero crossings.
It is really hard to imagine how a filter with a perfect LPF frequency response (as a sinc filter has) could be classified as unstable. Any sinusoidal input, for instance, is a bounded input with an obviously bounded output (either the same sinusoid or zero, depending on its frequency). However it indeed appears that the L1 criterion mentioned here would be violated by the sinc impulse response, which is stated to be an absolute test for stability/instability.
But never mind: I believe I see the problem. The sinc function extends to infinity in both negative and positive time so it cannot possibly be implemented as a causal filter, and this section is about causal filters (otherwise the concept of instability breaks down inasmuch as stable impulse responses with right hand plane zeros, if reversed in time, describe unstable systems). So I don't think the example is applicable.
And in any case, it could only be confusing to an average WP reader who is trying to LEARN about systems (since it's confusing to ME and I sort of thought I knew all about filter theory!). If the claim is true in some sense, then it stands more as a paradox or riddle than as useful information. Could someone remove this and put in a better example? And possibly (but here I'm not certain) restate the L1 criterion with a statement that it only applies to causal systems, or whatever qualifications are missing which make this result paradoxical or (I think) simply wrong? Interferometrist (talk) 12:14, 3 March 2011 (UTC)
- You are correct in saying "It is really hard to imagine how a filter with a perfect LPF frequency response (as a sinc filter has) could be classified as unstable." It is not unstable; neither is its time reversal. But it is also not bounded-input–bounded-output stable. So what? It is still a good illustration of the idea of BIBO stability. Dicklyon (talk) 06:17, 7 March 2011 (UTC)
LTI is not a widely known abbreviation - why use it?
[edit]I worked for about 30 years in this subject and never once heard it referred to as LTI systems theory. Is the name just the invention of one person? What strange things can happen in Wikipedia.JFB80 (talk) 05:48, 24 January 2016 (UTC)
- Try Googling "LTI system". --Bob K (talk) 00:19, 13 July 2017 (UTC)
Article about systems/system theory in general
[edit]I am not able to find a proper mathematical definition what a system in general is (a function that maps function (called input signals here) to functions (called output signals here)). There is this article here about LTI systems and an article about |time-invariant systems but there is no article about systems in general. I porpose that there should be a separate article discussing systems in general and defining some funcamental properties (time-invariance, linearity, ...) and showing examples of such systems. Fvultier (talk) 18:14, 12 July 2017 (UTC)
- A better place for this suggestion is Talk:System. --Bob K (talk) 00:27, 13 July 2017 (UTC)
Requested move 31 July 2018
[edit]- The following is a closed discussion of a requested move. Please do not modify it. Subsequent comments should be made in a new section on the talk page. Editors desiring to contest the closing decision should consider a move review. No further edits should be made to this section.
The result of the move request was: consensus to move the page to the proposed title at this time, per the discussion below. Dekimasuよ! 06:11, 7 August 2018 (UTC)
Linear time-invariant theory → Linear time-invariant system – The current title doesn't make sense. Neither does the similar phrase in the lead. Dicklyon (talk) 05:59, 31 July 2018 (UTC)
- This seems reasonable, as "Linear time-invariant system" is the common name for these objects. But I would drop the "theory" as redundant. We have linear system, time-invariant system, time-variant system, nonlinear system, etc and we should follow the same convention here. --
{{u|Mark viking}} {Talk}10:04, 31 July 2018 (UTC)- Yes, I agree, Linear time-invariant system is a better choice. I support that better proposal. Dicklyon (talk) 14:07, 31 July 2018 (UTC)
- Support the move to Linear time-invariant system as the common name for it. --
{{u|Mark viking}} {Talk}17:13, 31 July 2018 (UTC)
- I Support the proposal by Mark viking, that the title "Linear time-invariant system" is the most appropriate title, because the current title doesn't make sense.[1]Suman chowdhury 22 (talk) 17:28, 4 August 2018 (UTC)
- The above discussion is preserved as an archive of a requested move. Please do not modify it. Subsequent comments should be made in a new section on this talk page or in a move review. No further edits should be made to this section.
References
- ^ Oppenheim, Alan V.; Willsky, Alan S.; Nawab, S. Hamid. Signals and systems (2nd ed.). Prentice-Hall. p. 74. ISBN 9788120312463.
Lede rewrite
[edit]@Interferometrist:, thank you for your edits. The definition in the lede as currently written uses the titular terms themselves in the definition. It's like saying "a seed stitch is a stitch that uses a seed stitch technique to stitch". Also, WP:LEAD requires that unfamiliar terms be defined when used in the lede. Since the terms "linear" and "time-invariant" are part of the title of the subject article, it is reasonable to assume that folks coming to this article may be unfamiliar with those terms. Also, WP:LEAD advises that formulae be avoided in the lead when possible. My attempt at a rewrite was intended to address those issues. Can we rewrite the lede to be more accessible, without using the subject terms in the definition? Sparkie82 (t•c) 01:35, 11 September 2020 (UTC)
- Hi, yes thanks for your thoughts. Indeed I mentioned at the time of the change that I CHOOSE to not include the definitions of linearity and time-invariance in the lede itself because, especially linearity, is a subject in itself and could not be reasonably dealt with (yes I know you tried) in a few sentences. Moreover, I just used ONE definition of LTI systems but not the one that is the most significant. I could have said that "A LTI system is one that can be solved by convolution and has a frequency response." And .... by the way, that REQUIRES that it be linear and time-invariant. Either definition should be acceptable because they are mathematically equivalent. But of course I was using the literal definition but then saying what is significant about it, which is neither linearity nor time-invariance. If you really believe that it is important that the lede contain the definition of (possibly unfamiliar) terms it contains, then we need to move the first two paragraphs of #Overview to the lede. But I just made an edit which immediately directs one to the Overview section for those definitions, and I don't think any shorter explanation of linearity and time-invariance (let alone one without mathematical symbols!) would suffice.
- I see you tried very hard to define these in your 4 points but I think it came out rather clumsy especially because you tried to do it without using mathematical symbols. THAT made it difficult to read and understand -- because you were trying to do mathematics using words only (try doing that to convey the differential equation describing an RC lowpass circuit. I could, but it would be nearly unreadable!). When following wikipedia rules, you should always remember the rule about breaking rules where it's clearly called for. Also, I do not believe y=x*h would be called a "formula", or even an equation of significance, but rather showing the notation used for convolution (the main property of the term being defined!) as part of the same sentence that says it but which, I believe, simplifies/clarifies the sentence (the only point of mathematical notation, after all). By removing it you could say you followed the "rule" exactly, but I don't see any such imperative.
- But I'd like to see if others think y=x*h looks out of place. My only goal WAS to make the text accessible, as you say, so I'd like to see what in the lede isn't accessible to the average reader that would be looking this up (who would surely have some mathematical background, or they went to the wrong page). And we'll go from there, ok? Interferometrist (talk) 15:59, 11 September 2020 (UTC)
- My goal is make articles accessible to the widest possible audience while providing precision within the article as a whole, although I understand that some people don't share that goal for a variety of reasons. This article is not merely a mathematics article, it spans many disciplines. I don't remember how I came upon the article, I think maybe via signal processing (which is may be why I specified it in the scope). My formal math education stopped at beginning calculus and that was decades ago, but (with much effort consulting other sources) I was able to acquire a grasp of what this concept was about. As the article was written when I found it, that was impossible. In my opinion, the article is poorly written if the goal is to explain the concept in a way that many people will understand (not just mathematicians). I apparently don't have as much interest in this subject as you do, so I'll just leave you to it. However, for those who are "convoluted" by the current lede, I'm posted my rewrite here in case they find their way to the talk page. Sparkie82 (t•c) 11:58, 19 September 2020 (UTC)
- Listen, MY goal is also to make articles accessible to the widest possible audience while providing precision, and I think that is true of most all Wikipedia editors. Saying otherwise -- that is, imputing undesirable motives to other editors -- goes against Wikipedia's policy of assuming good faith (until proven otherwise, at which point the proper response is to just go ahead and edit and let the violator display their bad faith). The text you have written below is just an exact copy of your edit of 31 August at [1]. I explained earlier that I do not believe that your valiant attempt to describe linearity and time invariance in English while completely avoiding any mathematical terminology DID make the text clear and accessible to the widest possible audience (I'm not sure I would have understood it myself if I hadn't already). Moreover, I pointed out that linearity and time invariance are not what are most notable about this topic, even if they could be adequately defined in one sentence without mathematical symbols. Rather its the way these systems are solved and their wide applicabilty in the physical sciences and engineering. I tried to write one that is better in that light, but where an editor can see an improvement, I welcome their attempt to do so, but of course will challenge that when I think they are mistaken.
- Any terms used in the lede should be defined immediately in-line and/or through links to pages on those very subjects. Although LTI system theory could be called applied mathematics, the article is certainly not geared toward mathematicians, as you wrongly state, but indeed to the widest possible audience -- and that possible audience does NOT include people who do not already have some idea about the meaning of "linearity" (perhaps not the exact meaning used here), and so it is GOOD if that term scares someone away from the page. Any non-familiar terms are immediately linked to, and defined promptly. If your problem is that you think that definition needs to be in the lede itself (I don't), then just remove the first section break so that Overview becomes part of the lede. But if you do, I would argue that it's better as is.
- If there is a specific sentence, concept, or word in the lede that you think limits the readership of this article, then please point that out TO ME because I WOULD change it. I just don't see it, but maybe you do. Ok? Interferometrist (talk) 20:32, 20 September 2020 (UTC)
- My goal is make articles accessible to the widest possible audience while providing precision within the article as a whole, although I understand that some people don't share that goal for a variety of reasons. This article is not merely a mathematics article, it spans many disciplines. I don't remember how I came upon the article, I think maybe via signal processing (which is may be why I specified it in the scope). My formal math education stopped at beginning calculus and that was decades ago, but (with much effort consulting other sources) I was able to acquire a grasp of what this concept was about. As the article was written when I found it, that was impossible. In my opinion, the article is poorly written if the goal is to explain the concept in a way that many people will understand (not just mathematicians). I apparently don't have as much interest in this subject as you do, so I'll just leave you to it. However, for those who are "convoluted" by the current lede, I'm posted my rewrite here in case they find their way to the talk page. Sparkie82 (t•c) 11:58, 19 September 2020 (UTC)
More understandable introduction to the concept
[edit]I propose a more understandable introduction to this topic as follows:
- In signal analysis and other fields of study, a linear time-invariant system is a system that meets the following criteria: 1) the output signal is proportional to the input signal; 2) the scale of the proportion doesn't vary throughout the range of inputs under analysis; 3) the relationship between the input and output (including the scale) doesn't vary over time; and 4) in the case of multiple input signals, the addition operation on the inputs is preserved in the output. Linear time-invariance also finds application in image processing and field theory, where the LTI systems have spatial dimensions instead of, or in addition to, a temporal dimension. These systems may be referred to as linear translation-invariant to give the terminology the most general reach. In the case of generic discrete-time (i.e., sampled) systems, linear shift-invariant is the corresponding term. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors.[1]. Sparkie82 (t•c) 11:59, 19 September 2020 (UTC)
References
[edit]- ^ Hespanha 2009, p. 78.
What are some examples of resistors/capacitors/inductors whose values significantly vary that are not simply called resistors/capacitors/inductors?
[edit]Hi @Interferometrist:! Given the recent revert, can you please give some examples of the following statement?:
- "Resistors/capacitors/inductors which substantially change their values (under normal operating circumstances) are NOT simply called resistors/capacitors/inductors, they have their own names, that's all."
And secondly, if the previous statement is true, does it imply that the phrase "a non-linear resistor" is wrong because such a device would not be called a resistor?
Thanks in advance. --Alej27 (talk) 01:16, 3 July 2021 (UTC)
- Well sure, I can answer that. Or actually two matters you have brought up. First are adjustable resistors/capacitors/inductors -> variable resistors, potentiometers, rheostats; variable/tuning capacitors, adjustable inductors. But those are in a catagory I would call LTI because the adjustments are on a much longer time scale than than the waveforms, so with any one adjustment it is LTI and after adjustment a different set of equations hold.
- More interesting are thermistors, photoresistors, force or strain sensors, capacitive microphones, whose R/C/L values depend on external circumstances. When their values vary slowly with respect to the signals, the above applies. Otherwise they are non-time-invariant. None are simply called R/C/L. Or varactors used in the small signal regime with a slowly-varying tuning voltage, also see above.
- And then there are components whose values vary DUE to the signals (voltage/current) applied to them. Thermistors used for surge control or (in the old days) demagnitization, where the "signal" is order of seconds; varactors used in the large signal regime; inductors intentionally driven to saturation or taking advantage of hysteresis (core memory, if you're old enough). These cannot generally be treated as linear components.
- Those quickly come to mind and I don't want to spend time writing a complete list. The important point (and answering your second question) is that you never just call them R/C/L EXCEPT as in the first paragraph when they are "constant" values over a period long compared to the signals, in which case they are simply regarded (for the sake of circuit analysis) as LTI -- but still they have unique names! When you just say resistor you are implying an ideal resistor (by ohms law) or one which is approximately so given the way it's being used so you analyze it as such.
- Everyone in electronics understands all this, but a newbie reading the sort of text you wrote might get the impression that they NEED to point out when their values are constant. No, you don't, that's the default. OK? Interferometrist (talk) 21:06, 3 July 2021 (UTC)
- "No, you don't, that's the default." That made me click the idea. I agree. --Alej27 (talk) 23:36, 3 July 2021 (UTC)
Merge from Time-invariant system
[edit]- The following discussion is closed. Please do not modify it. Subsequent comments should be made in a new section. A summary of the conclusions reached follows.
- The result of the discussion was no consensus for a merge in either direction. Shhhnotsoloud (talk) 18:48, 14 July 2022 (UTC)
I proposed that Time-invariant system be removed as a separate topic (it isn't) and its current contents be merged into this article. It may already be sufficiently dealt with, but if anyone sees content on the other page that would help here, please go ahead and edit that in. Interferometrist (talk) 20:51, 5 July 2021 (UTC)
- Oppose, on the grounds that if anything the merge should be in the reverse direction (to the broader topic). However, Linear time-invariant system is a sufficiently important topic that it warrants separate coverage. Hence, I'd recommend keeping the current structure. Klbrain (talk) 11:59, 19 December 2021 (UTC)
- Oppose Time-variant system should be merged into this instead — Preceding unsigned comment added by Marcusmueller ettus (talk • contribs) 15:00, 28 March 2022 (UTC)
Merge from Time-variant system
[edit]I proposed that Time-variant system be removed as a separate topic (it isn't. It isn't even a term used in practice) and its current contents be merged into this article. It may already be sufficiently dealt with, but if anyone sees content on the other page that would help here, please go ahead and edit that in. Interferometrist (talk) 14:49, 6 July 2021 (UTC)
- Oppose, as above. Klbrain (talk) 12:01, 19 December 2021 (UTC)
- Support, as time-variant is "default unless specified otherwise", and any system that is not one is automatically the other. Also, the Linear time-variant article is just really really not good, the definition in there is confusing to students (I say as someone who taught stochastic systems and basics of digital comms), and it would be much better to give that definition in a section of this article. — Preceding unsigned comment added by Marcusmueller ettus (talk • contribs) 15:03, 28 March 2022 (UTC)
- C-Class Systems articles
- High-importance Systems articles
- Systems articles in control theory
- WikiProject Systems articles
- C-Class Time articles
- Low-importance Time articles
- C-Class mathematics articles
- Low-priority mathematics articles
- C-Class electronic articles
- Low-importance electronic articles
- WikiProject Electronics articles
























































![{\displaystyle y[n_{1}]=\sum _{n_{2}=-\infty }^{\infty }h[n_{1},n_{2}]\,x[n_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013b13f33a0bcdb7516b4614356aa34b80e65066)
![{\displaystyle h[n_{1},n_{2}]=h[n_{1}+m,n_{2}+m]\qquad \forall \,m\in \mathbb {Z} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c77b7b4e1a52d140be47803ac6d5b0544e62e7d)

![{\displaystyle h[n_{1},n_{2}]=h[n_{1}-n_{2},0].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbe2f0643e2c7ff62e7c2747f79449bbde1035e)