Carbonic acid
| |

| |
| Names | |
|---|---|
| IUPAC name
Carbonic acid[1]
| |
Other names
| |
| Identifiers | |
3D model (JSmol)
|
|
| ChEBI | |
| ChEMBL | |
| ChemSpider | |
| DrugBank | |
| ECHA InfoCard | 100.133.015 |
| EC Number |
|
| 25554 | |
| KEGG | |
PubChem CID
|
|
| UNII | |
CompTox Dashboard (EPA)
|
|
| |
| |
| Properties | |
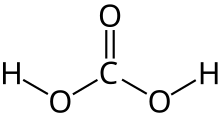
| H 2CO 3 | |
| Appearance | Colorless gas |
| Melting point | −53 °C (−63 °F; 220 K)[2] (sublimes) |
| Boiling point | 127 °C (261 °F; 400 K) (decomposes) |
| Reacts to form carbon dioxide and water | |
| Acidity (pKa) | pKa1 = 3.6 at 25 °C pKa2 = 10.329 |
| Conjugate base | Bicarbonate, carbonate |
| Hazards | |
| NFPA 704 (fire diamond) | |
| Structure | |
| monoclinic | |
| p21/c, No. 14 | |
| - | |
a = 5.392 Å, b = 6.661 Å, c = 5.690 Å α = 90°, β = 92.66°, γ = 90°[3] (D
2CO 3 at 1.85 GPa, 298 K) | |
Lattice volume (V)
|
204.12 Å3 |
Formula units (Z)
|
4 formula per cell |
Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa).
| |
Carbonic acid is a chemical compound with the chemical formula H2CO3. The molecule rapidly converts to water and carbon dioxide in the presence of water. However, in the absence of water, it is (contrary to popular belief) quite stable at room temperature.[4][5] The interconversion of carbon dioxide and carbonic acid is related to the breathing cycle of animals and the acidification of natural waters.[3]
In biochemistry and physiology, the name "carbonic acid" is sometimes applied to aqueous solutions of carbon dioxide. These chemical species play an important role in the bicarbonate buffer system, used to maintain acid–base homeostasis.[6]
Terminology in biochemical literature[edit]
In chemistry, the term "carbonic acid" strictly refers to the chemical compound with the formula H
2CO
3. Some biochemistry literature effaces the distinction between carbonic acid and carbon dioxide dissolved in extracellular fluid.
In physiology, carbon dioxide excreted by the lungs may be called volatile acid or respiratory acid.
Anhydrous carbonic acid[edit]
At ambient temperatures, pure carbonic acid is a stable gas.[5] There are two main methods to produce anhydrous carbonic acid: reaction of hydrogen chloride and potassium bicarbonate at 100 K in methanol and proton irradiation of pure solid carbon dioxide.[2] Chemically, it behaves as a diprotic Brønsted acid.[7][8]
Carbonic acid monomers exhibit three conformational isomers: cis–cis, cis–trans, and trans–trans.[9]
At low temperatures and atmospheric pressure, solid carbonic acid is amorphous and lacks Bragg peaks in X-ray diffraction.[10] But at high pressure, carbonic acid crystallizes, and modern analytical spectroscopy can measure its geometry.
According to neutron diffraction of dideuterated carbonic acid (D
2CO
3) in a hybrid clamped cell (Russian alloy/copper-beryllium) at 1.85 GPa, the molecules are planar and form dimers joined by pairs of hydrogen bonds. All three C-O bonds are nearly equidistant at 1.34 Å, intermediate between typical C-O and C=O distances (respectively 1.43 and 1.23 Å). The unusual C-O bond lengths are attributed to delocalized π bonding in the molecule's center and extraordinarily strong hydrogen bonds. The same effects also induce a very short O—O separation (2.13 Å), through the 136° O-H-O angle imposed by the doubly hydrogen-bonded 8-membered rings.[3] Longer O—O distances are observed in strong intramolecular hydrogen bonds, e.g. in oxalic acid, where the distances exceed 2.4 Å.[10]
In aqueous solution[edit]
In even a slight presence of water, carbonic acid dehydrates to carbon dioxide and water, which then catalyzes further decomposition.[5] For this reason, carbon dioxide can be considered the carbonic acid anhydride.
The hydration equilibrium constant at 25 °C is [H
2CO
3]/[CO2] ≈ 1.7×10−3 in pure water[11] and ≈ 1.2×10−3 in seawater.[12] Hence the majority of carbon dioxide at geophysical or biological air-water interfaces does not convert to carbonic acid, remaining dissolved CO2 gas. However, the uncatalyzed equilibrium is reached quite slowly: the rate constants are 0.039 s−1 for hydration and 23 s−1 for dehydration.
In biological solutions[edit]
In the presence of the enzyme carbonic anhydrase, equilibrium is instead reached rapidly, and the following reaction takes precedence:[13]
When the created carbon dioxide exceeds its solubility, gas evolves and a third equilibrium
The two reactions can be combined for the equilibrium in solution:
Under high CO2 partial pressure[edit]
In the beverage industry, sparkling or "fizzy water" is usually referred to as carbonated water. It is made by dissolving carbon dioxide under a small positive pressure in water. Many soft drinks treated the same way effervesce.
Significant amounts of molecular H
2CO
3 exist in aqueous solutions subjected to pressures of multiple gigapascals (tens of thousands of atmospheres) in planetary interiors.[15][16] Pressures of 0.6–1.6 GPa at 100 K, and 0.75–1.75 GPa at 300 K are attained in the cores of large icy satellites such as Ganymede, Callisto, and Titan, where water and carbon dioxide are present. Pure carbonic acid, being denser, is expected to have sunk under the ice layers and separate them from the rocky cores of these moons.[17]
Relationship to bicarbonate and carbonate[edit]

Carbonic acid is the formal Brønsted–Lowry conjugate acid of the bicarbonate anion, stable in alkaline solution. The protonation constants have been measured to great precision, but depend on overall ionic strength I. The two equilibria most easily measured are as follows:
To interpret these numbers, note that two chemical species in an acid equilibrium are equiconcentrated when pK = pH. In particular, the extracellular fluid (cytosol) in biological systems exhibits pH ≈ 7.2, so that carbonic acid will be almost 50%-dissociated at equilibrium.
Ocean acidification[edit]

The Bjerrum plot shows typical equilibrium concentrations, in solution, in seawater, of carbon dioxide and the various species derived from it, as a function of pH.[7][8] As human industrialization has increased the proportion of carbon dioxide in Earth's atmosphere, the proportion of carbon dioxide dissolved in sea- and freshwater as carbonic acid is also expected to increase. This rise in dissolved acid is also expected to acidify those waters, generating a decrease in pH.[20][21] It has been estimated that the increase in dissolved carbon dioxide has already caused the ocean's average surface pH to decrease by about 0.1 from pre-industrial levels.
Further reading[edit]
 "Climate and Carbonic Acid" in Popular Science Monthly Volume 59, July 1901
"Climate and Carbonic Acid" in Popular Science Monthly Volume 59, July 1901- Welch, M. J.; Lifton, J. F.; Seck, J. A. (1969). "Tracer studies with radioactive oxygen-15. Exchange between carbon dioxide and water". J. Phys. Chem. 73 (335): 3351. doi:10.1021/j100844a033.
- Jolly, W. L. (1991). Modern Inorganic Chemistry (2nd ed.). McGraw-Hill. ISBN 978-0-07-112651-9.
- Moore, M. H.; Khanna, R. (1991). "Infrared and Mass Spectral Studies of Proton Irradiated H2O+CO2 Ice: Evidence for Carbonic Acid Ice: Evidence for Carbonic Acid". Spectrochimica Acta. 47A (2): 255–262. Bibcode:1991AcSpA..47..255M. doi:10.1016/0584-8539(91)80097-3.
- W. Hage, K. R. Liedl; Liedl, E.; Hallbrucker, A; Mayer, E (1998). "Carbonic Acid in the Gas Phase and Its Astrophysical Relevance". Science. 279 (5355): 1332–5. Bibcode:1998Sci...279.1332H. doi:10.1126/science.279.5355.1332. PMID 9478889.
- Hage, W.; Hallbrucker, A.; Mayer, E. (1995). "A Polymorph of Carbonic Acid and Its Possible Astrophysical Relevance". J. Chem. Soc. Faraday Trans. 91 (17): 2823–6. Bibcode:1995JCSFT..91.2823H. doi:10.1039/ft9959102823.
References[edit]
- ^ "Front Matter". Nomenclature of Organic Chemistry: IUPAC Recommendations and Preferred Names 2013 (Blue Book). Cambridge: The Royal Society of Chemistry. 2014. pp. P001–4. doi:10.1039/9781849733069-FP001. ISBN 978-0-85404-182-4.
- ^ a b W. Hage, K. R. Liedl; Liedl, E.; Hallbrucker, A; Mayer, E (1998). "Carbonic Acid in the Gas Phase and Its Astrophysical Relevance". Science. 279 (5355): 1332–5. Bibcode:1998Sci...279.1332H. doi:10.1126/science.279.5355.1332. PMID 9478889.
- ^ a b c Benz, Sebastian; Chen, Da; Möller, Andreas; Hofmann, Michael; Schnieders, David; Dronskowski, Richard (September 2022). "The Crystal Structure of Carbonic Acid". Inorganics. 10 (9): 132. doi:10.3390/inorganics10090132. ISSN 2304-6740.
- ^ Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. p. 310. ISBN 978-0-08-037941-8.
- ^ a b c Loerting, Thomas; Tautermann, Christofer; Kroemer, Romano T.; Kohl, Ingrid; Hallbrucker, Andreas; Mayer, Erwin; Liedl, Klaus R.; Loerting, Thomas; Tautermann, Christofer; Kohl, Ingrid; Hallbrucker, Andreas; Erwin, Mayer; Liedl, Klaus R. (2000). "On the Surprising Kinetic Stability of Carbonic Acid (H2CO3)". Angewandte Chemie International Edition. 39 (5): 891–4. doi:10.1002/(SICI)1521-3773(20000303)39:5<891::AID-ANIE891>3.0.CO;2-E. PMID 10760883.
- ^ Acid-Base Physiology 2.1 – Acid-Base Balance by Kerry Brandis.
- ^ a b Pangotra, Dhananjai; Csepei, Lénárd-István; Roth, Arne; Ponce de León, Carlos; Sieber, Volker; Vieira, Luciana (2022). "Anodic production of hydrogen peroxide using commercial carbon materials". Applied Catalysis B: Environmental. 303: 120848. doi:10.1016/j.apcatb.2021.120848. S2CID 240250750.
- ^ a b Andersen, C. B. (2002). "Understanding carbonate equilibria by measuring alkalinity in experimental and natural systems". Journal of Geoscience Education. 50 (4): 389–403. Bibcode:2002JGeEd..50..389A. doi:10.5408/1089-9995-50.4.389. S2CID 17094010.
- ^ Loerting, Thomas; Bernard, Juergen (2010). "Aqueous Carbonic Acid (H2CO3)". ChemPhysChem (11): 2305–9. doi:10.1002/cphc.201000220.
- ^ a b Winkel, Katrin; Hage, Wolfgang; Loerting, Thomas; Price, Sarah L.; Mayer, Erwin (2007). "Carbonic Acid: From Polyamorphism to Polymorphism". Journal of the American Chemical Society. 129 (45): 13863–71. doi:10.1021/ja073594f. PMID 17944463.
- ^ Housecroft, C.E.; Sharpe, A.G. (2005). Inorganic Chemistry (2nd ed.). Prentice-Pearson-Hall. p. 368. ISBN 0-13-039913-2. OCLC 56834315.
- ^ Soli, A. L.; R. H. Byrne (2002). "CO2 system hydration and dehydration kinetics and the equilibrium CO2/H2CO3 ratio in aqueous NaCl solution". Marine Chemistry. 78 (2–3): 65–73. doi:10.1016/S0304-4203(02)00010-5.
- ^ Lindskog S (1997). "Structure and mechanism of carbonic anhydrase". Pharmacology & Therapeutics. 74 (1): 1–20. doi:10.1016/S0163-7258(96)00198-2. PMID 9336012.
- ^ Sander, Rolf; Acree, William E.; Visscher, Alex De; Schwartz, Stephen E.; Wallington, Timothy J. (1 January 2022). "Henry's law constants (IUPAC Recommendations 2021)". Pure and Applied Chemistry. 94 (1): 71–85. doi:10.1515/pac-2020-0302. ISSN 1365-3075.
- ^ Wang, Hongbo; Zeuschner, Janek; Eremets, Mikhail; Troyan, Ivan; Williams, Jonathon (27 January 2016). "Stable solid and aqueous H2CO3 from CO2 and H2O at high pressure and high temperature". Scientific Reports. 6 (1): 19902. Bibcode:2016NatSR...619902W. doi:10.1038/srep19902. PMC 4728613. PMID 26813580.
- ^ Stolte, Nore; Pan, Ding (4 July 2019). "Large presence of carbonic acid in CO2-rich aqueous fluids under Earth's mantle conditions". The Journal of Physical Chemistry Letters. 10 (17): 5135–41. arXiv:1907.01833. doi:10.1021/acs.jpclett.9b01919. PMID 31411889. S2CID 195791860.
- ^ G. Saleh; A. R. Oganov (2016). "Novel Stable Compounds in the C-H-O Ternary System at High Pressure". Scientific Reports. 6: 32486. Bibcode:2016NatSR...632486S. doi:10.1038/srep32486. PMC 5007508. PMID 27580525.
- ^ IUPAC (2006). "Stability constants" (database).
- ^ Pines, Dina; Ditkovich, Julia; Mukra, Tzach; Miller, Yifat; Kiefer, Philip M.; Daschakraborty, Snehasis; Hynes, James T.; Pines, Ehud (2016). "How Acidic Is Carbonic Acid?". J Phys Chem B. 120 (9): 2440–51. doi:10.1021/acs.jpcb.5b12428. PMC 5747581. PMID 26862781.
- ^ Caldeira, K.; Wickett, M. E. (2003). "Anthropogenic carbon and ocean pH". Nature. 425 (6956): 365. Bibcode:2001AGUFMOS11C0385C. doi:10.1038/425365a. PMID 14508477. S2CID 4417880.
- ^ Sabine, C. L. (2004). "The Oceanic Sink for Anthropogenic CO2". Science. 305 (5682): 367–371. Bibcode:2004Sci...305..367S. doi:10.1126/science.1097403. hdl:10261/52596. PMID 15256665. S2CID 5607281. Archived from the original on 6 July 2008. Retrieved 22 June 2021.




![{\displaystyle {\begin{aligned}{\ce {HCO3^{-}{}+ H+{}<=> CO2(soln){}+ H2O}}&&K_{3}={\frac {[{\ce {H+}}][{\ce {HCO3^-}}]}{[{\ce {CO2(soln)}}]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3efe827e57da672cf1c617cebeddb8cf04baa81)
![{\displaystyle {\begin{aligned}{\ce {CO3^{2-}{}+ H+{}<=> HCO3^-}}&&\beta _{1}={\frac {[{\ce {HCO3^-}}]}{[{\ce {H+}}][{\ce {CO3^{2-}}}]}}\\{\ce {CO3^{2-}{}+ 2H+{}<=> H2CO3}}&&\beta _{2}={\frac {[{\ce {H2CO3}}]}{[{\ce {H+}}]^{2}[{\ce {CO3^{2-}}}]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09f8d396f1143f199cf1136f1ad60c7ce873b848)

