Negative feedback
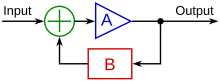
Negative feedback (or balancing feedback) occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. A classic example of negative feedback is a heating system thermostat — when the temperature gets high enough, the heater is turned OFF. When the temperature gets too cold, the heat is turned back ON. In each case the "feedback" generated by the thermostat "negates" the trend.
The opposite tendency — called positive feedback — is when a trend is positively reinforced, creating amplification, such as the squealing "feedback" loop that can occur when a mic is brought too close to a speaker which is amplifying the very sounds the mic is picking up, or the runaway heating and ultimate meltdown of a nuclear reactor which has a positive temperature coefficient of reactivity.
Whereas positive feedback tends to lead to instability via exponential growth, oscillation or chaotic behavior, negative feedback generally promotes stability. Negative feedback tends to promote a settling to equilibrium, and reduces the effects of perturbations. Negative feedback loops in which just the right amount of correction is applied with optimum timing, can be very stable, accurate, and responsive.
Negative feedback is widely used in mechanical and electronic engineering, and also within living organisms,[1][2] and can be seen in many other fields from chemistry and economics to physical systems such as the climate. General negative feedback systems are studied in control systems engineering.
Negative feedback loops also play an integral role in maintaining the atmospheric balance in various systems on Earth. One such feedback system is the interaction between solar radiation, cloud cover, and planet temperature.

General description
[edit]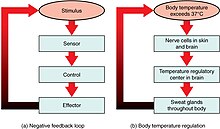
In many physical and biological systems, qualitatively different influences can oppose each other. For example, in biochemistry, one set of chemicals drives the system in a given direction, whereas another set of chemicals drives it in an opposing direction. If one or both of these opposing influences are non-linear, equilibrium point(s) result.
In biology, this process (in general, biochemical) is often referred to as homeostasis; whereas in mechanics, the more common term is equilibrium.
In engineering, mathematics and the physical, and biological sciences, common terms for the points around which the system gravitates include: attractors, stable states, eigenstates/eigenfunctions, equilibrium points, and setpoints.
In control theory, negative refers to the sign of the multiplier in mathematical models for feedback. In delta notation, −Δoutput is added to or mixed into the input. In multivariate systems, vectors help to illustrate how several influences can both partially complement and partially oppose each other.[3]
Some authors, in particular with respect to modelling business systems, use negative to refer to the reduction in difference between the desired and actual behavior of a system.[4][5] In a psychology context, on the other hand, negative refers to the valence of the feedback – attractive versus aversive, or praise versus criticism.[6]
In contrast, positive feedback is feedback in which the system responds so as to increase the magnitude of any particular perturbation, resulting in amplification of the original signal instead of stabilization. Any system in which there is positive feedback together with a gain greater than one will result in a runaway situation. Both positive and negative feedback require a feedback loop to operate.
However, negative feedback systems can still be subject to oscillations. This is caused by a phase shift around any loop. Due to these phase shifts the feedback signal of some frequencies can ultimately become in phase with the input signal and thus turn into positive feedback, creating a runaway condition. Even before the point where the phase shift becomes 180 degrees, stability of the negative feedback loop will become compromised, leading to increasing under- and overshoot following a disturbance. This problem is often dealt with by attenuating or changing the phase of the problematic frequencies in a design step called compensation. Unless the system naturally has sufficient damping, many negative feedback systems have low pass filters or dampers fitted.
Examples
[edit]- Mercury thermostats (circa 1600) using expansion and contraction of columns of mercury in response to temperature changes were used in negative feedback systems to control vents in furnaces, maintaining a steady internal temperature.
- In the invisible hand of the market metaphor of economic theory (1776), reactions to price movements provide a feedback mechanism to match supply and demand.
- In centrifugal governors (1788), negative feedback is used to maintain a near-constant speed of an engine, irrespective of the load or fuel-supply conditions.
- In a steering engine (1866), power assistance is applied to the rudder with a feedback loop, to maintain the direction set by the steersman.
- In servomechanisms, the speed or position of an output, as determined by a sensor, is compared to a set value, and any error is reduced by negative feedback to the input.
- In audio amplifiers, negative feedback flattens frequency response, reduces distortion, minimises the effect of manufacturing variations in component parameters, and compensates for changes in characteristics due to temperature change.
- In analog computing, feedback around operational amplifiers is used to generate mathematical functions such as addition, subtraction, integration, differentiation, logarithm, and antilog functions.
- In delta-sigma analog-to-digital and digital-to-analog converters (particularly for high quality audio), a negative feedback loop is used to repeatedly correct accumulated quantization error during conversion.
- In a phase locked loop (1932), feedback is used to maintain a generated alternating waveform in a constant phase to a reference signal. In many implementations the generated waveform is the output, but when used as a demodulator in an FM radio receiver, the error feedback voltage serves as the demodulated output signal. If there is a frequency divider between the generated waveform and the phase comparator, the device acts as a frequency multiplier.
- In organisms, feedback enables various measures (e.g. body temperature, or blood sugar level) to be maintained within a desired range by homeostatic processes.
Detailed implementations
[edit]Error-controlled regulation
[edit]

One use of feedback is to make a system (say T) self-regulating to minimize the effect of a disturbance (say D). Using a negative feedback loop, a measurement of some variable (for example, a process variable, say E) is subtracted from a required value (the 'set point') to estimate an operational error in system status, which is then used by a regulator (say R) to reduce the gap between the measurement and the required value.[8][9] The regulator modifies the input to the system T according to its interpretation of the error in the status of the system. This error may be introduced by a variety of possible disturbances or 'upsets', some slow and some rapid.[10] The regulation in such systems can range from a simple 'on-off' control to a more complex processing of the error signal.[11]
In this framework, the physical form of a signal may undergo multiple transformations. For example, a change in weather may cause a disturbance to the heat input to a house (as an example of the system T) that is monitored by a thermometer as a change in temperature (as an example of an 'essential variable' E). This quantity, then, is converted by the thermostat (a 'comparator') into an electrical error in status compared to the 'set point' S, and subsequently used by the regulator (containing a 'controller' that commands gas control valves and an ignitor) ultimately to change the heat provided by a furnace (an 'effector') to counter the initial weather-related disturbance in heat input to the house.[12]
Error controlled regulation is typically carried out using a Proportional-Integral-Derivative Controller (PID controller). The regulator signal is derived from a weighted sum of the error signal, integral of the error signal, and derivative of the error signal. The weights of the respective components depend on the application.[13]
Mathematically, the regulator signal is given by:
where
- is the integral time
- is the derivative time
Negative feedback amplifier
[edit]The negative feedback amplifier was invented by Harold Stephen Black at Bell Laboratories in 1927, and granted a patent in 1937 (US Patent 2,102,671)[14] "a continuation of application Serial No. 298,155, filed August 8, 1928 ...").[15][16]
- "The patent is 52 pages long plus 35 pages of figures. The first 43 pages amount to a small treatise on feedback amplifiers!"[16]
There are many advantages to feedback in amplifiers.[17] In design, the type of feedback and amount of feedback are carefully selected to weigh and optimize these various benefits.
Advantages of negative voltage feedback in amplifiers
- It reduces non-linear distortion, that is, it has higher fidelity.
- It increases circuit stability: that is, the gain remains stable though there are variations in ambient temperature, frequency and signal amplitude.
- It increases bandwidth slightly.
- It modifies the input and output impedances.
- Harmonic, phase, amplitude, and frequency distortions are all reduced considerably.
- Noise is reduced considerably.
Though negative feedback has many advantages, amplifiers with feedback can oscillate. See the article on step response. They may even exhibit instability. Harry Nyquist of Bell Laboratories proposed the Nyquist stability criterion and the Nyquist plot that identify stable feedback systems, including amplifiers and control systems.
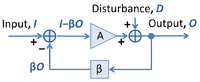
The figure shows a simplified block diagram of a negative feedback amplifier.
The feedback sets the overall (closed-loop) amplifier gain at a value:
where the approximate value assumes βA >> 1. This expression shows that a gain greater than one requires β < 1. Because the approximate gain 1/β is independent of the open-loop gain A, the feedback is said to 'desensitize' the closed-loop gain to variations in A (for example, due to manufacturing variations between units, or temperature effects upon components), provided only that the gain A is sufficiently large.[19] In this context, the factor (1+βA) is often called the 'desensitivity factor',[20][21] and in the broader context of feedback effects that include other matters like electrical impedance and bandwidth, the 'improvement factor'.[22]
If the disturbance D is included, the amplifier output becomes:
which shows that the feedback reduces the effect of the disturbance by the 'improvement factor' (1+β A). The disturbance D might arise from fluctuations in the amplifier output due to noise and nonlinearity (distortion) within this amplifier, or from other noise sources such as power supplies.[23][24]
The difference signal I–βO at the amplifier input is sometimes called the "error signal".[25] According to the diagram, the error signal is:
From this expression, it can be seen that a large 'improvement factor' (or a large loop gain βA) tends to keep this error signal small.
Although the diagram illustrates the principles of the negative feedback amplifier, modeling a real amplifier as a unilateral forward amplification block and a unilateral feedback block has significant limitations.[26] For methods of analysis that do not make these idealizations, see the article Negative feedback amplifier.
Operational amplifier circuits
[edit]
The operational amplifier was originally developed as a building block for the construction of analog computers, but is now used almost universally in all kinds of applications including audio equipment and control systems.
Operational amplifier circuits typically employ negative feedback to get a predictable transfer function. Since the open-loop gain of an op-amp is extremely large, a small differential input signal would drive the output of the amplifier to one rail or the other in the absence of negative feedback. A simple example of the use of feedback is the op-amp voltage amplifier shown in the figure.
The idealized model of an operational amplifier assumes that the gain is infinite, the input impedance is infinite, output resistance is zero, and input offset currents and voltages are zero. Such an ideal amplifier draws no current from the resistor divider.[28] Ignoring dynamics (transient effects and propagation delay), the infinite gain of the ideal op-amp means this feedback circuit drives the voltage difference between the two op-amp inputs to zero.[28] Consequently, the voltage gain of the circuit in the diagram, assuming an ideal op amp, is the reciprocal of feedback voltage division ratio β:
- .
A real op-amp has a high but finite gain A at low frequencies, decreasing gradually at higher frequencies. In addition, it exhibits a finite input impedance and a non-zero output impedance. Although practical op-amps are not ideal, the model of an ideal op-amp often suffices to understand circuit operation at low enough frequencies. As discussed in the previous section, the feedback circuit stabilizes the closed-loop gain and desensitizes the output to fluctuations generated inside the amplifier itself.[29]
Areas of application
[edit]Mechanical engineering
[edit]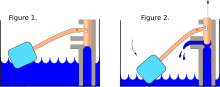
An example of the use of negative feedback control is the ballcock control of water level (see diagram), or a pressure regulator. In modern engineering, negative feedback loops are found in engine governors, fuel injection systems and carburettors. Similar control mechanisms are used in heating and cooling systems, such as those involving air conditioners, refrigerators, or freezers.
Biology
[edit]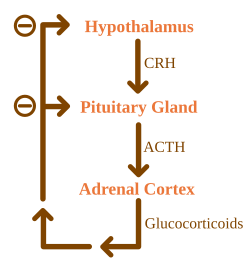
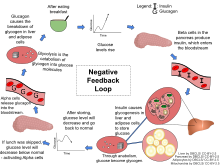
Some biological systems exhibit negative feedback such as the baroreflex in blood pressure regulation and erythropoiesis. Many biological processes (e.g., in the human anatomy) use negative feedback. Examples of this are numerous, from the regulating of body temperature, to the regulating of blood glucose levels. The disruption of feedback loops can lead to undesirable results: in the case of blood glucose levels, if negative feedback fails, the glucose levels in the blood may begin to rise dramatically, thus resulting in diabetes.
For hormone secretion regulated by the negative feedback loop: when gland X releases hormone X, this stimulates target cells to release hormone Y. When there is an excess of hormone Y, gland X "senses" this and inhibits its release of hormone X. As shown in the figure, most endocrine hormones are controlled by a physiologic negative feedback inhibition loop, such as the glucocorticoids secreted by the adrenal cortex. The hypothalamus secretes corticotropin-releasing hormone (CRH), which directs the anterior pituitary gland to secrete adrenocorticotropic hormone (ACTH). In turn, ACTH directs the adrenal cortex to secrete glucocorticoids, such as cortisol. Glucocorticoids not only perform their respective functions throughout the body but also negatively affect the release of further stimulating secretions of both the hypothalamus and the pituitary gland, effectively reducing the output of glucocorticoids once a sufficient amount has been released.[30]
Chemistry
[edit]Closed systems containing substances undergoing a reversible chemical reaction can also exhibit negative feedback in accordance with Le Chatelier's principle which shift the chemical equilibrium to the opposite side of the reaction in order to reduce a stress. For example, in the reaction
- N2 + 3 H2 ⇌ 2 NH3 + 92 kJ/mol
If a mixture of the reactants and products exists at equilibrium in a sealed container and nitrogen gas is added to this system, then the equilibrium will shift toward the product side in response. If the temperature is raised, then the equilibrium will shift toward the reactant side which, since the reverse reaction is endothermic, will partially reduce the temperature.
Self-organization
[edit]Self-organization is the capability of certain systems "of organizing their own behavior or structure".[31] There are many possible factors contributing to this capacity, and most often positive feedback is identified as a possible contributor. However, negative feedback also can play a role.[32]
Economics
[edit]In economics, automatic stabilisers are government programs that are intended to work as negative feedback to dampen fluctuations in real GDP.
Mainstream economics asserts that the market pricing mechanism operates to match supply and demand, because mismatches between them feed back into the decision-making of suppliers and demanders of goods, altering prices and thereby reducing any discrepancy. However Norbert Wiener wrote in 1948:
- "There is a belief current in many countries and elevated to the rank of an official article of faith in the United States that free competition is itself a homeostatic process... Unfortunately the evidence, such as it is, is against this simple-minded theory."[33]
The notion of economic equilibrium being maintained in this fashion by market forces has also been questioned by numerous heterodox economists such as financier George Soros[34] and leading ecological economist and steady-state theorist Herman Daly, who was with the World Bank in 1988–1994.[35]
Environmental Science
[edit]
A basic and common example of a negative feedback system in the environment is the interaction among cloud cover, plant growth, solar radiation, and planet temperature.[38] As incoming solar radiation increases, planet temperature increases. As the temperature increases, the amount of plant life that can grow increases. This plant life can then make products such as sulfur which produce more cloud cover. An increase in cloud cover leads to higher albedo, or surface reflectivity, of the Earth. As albedo increases, however, the amount of solar radiation decreases.[39] This, in turn, affects the rest of the cycle.
Cloud cover, and in turn planet albedo and temperature, is also influenced by the hydrological cycle.[40] As planet temperature increases, more water vapor is produced, creating more clouds.[41] The clouds then block incoming solar radiation, lowering the temperature of the planet. This interaction produces less water vapor and therefore less cloud cover. The cycle then repeats in a negative feedback loop. In this way, negative feedback loops in the environment have a stabilizing effect.[42]
History
[edit]Negative feedback as a control technique may be seen in the refinements of the water clock introduced by Ktesibios of Alexandria in the 3rd century BCE. Self-regulating mechanisms have existed since antiquity, and were used to maintain a constant level in the reservoirs of water clocks as early as 200 BCE.[43]

Negative feedback was implemented in the 17th century. Cornelius Drebbel had built thermostatically controlled incubators and ovens in the early 1600s,[44] and centrifugal governors were used to regulate the distance and pressure between millstones in windmills.[45] James Watt patented a form of governor in 1788 to control the speed of his steam engine, and James Clerk Maxwell in 1868 described "component motions" associated with these governors that lead to a decrease in a disturbance or the amplitude of an oscillation.[46]
The term "feedback" was well established by the 1920s, in reference to a means of boosting the gain of an electronic amplifier.[3] Friis and Jensen described this action as "positive feedback" and made passing mention of a contrasting "negative feed-back action" in 1924.[47] Harold Stephen Black came up with the idea of using negative feedback in electronic amplifiers in 1927, submitted a patent application in 1928,[15] and detailed its use in his paper of 1934, where he defined negative feedback as a type of coupling that reduced the gain of the amplifier, in the process greatly increasing its stability and bandwidth.[48][49]
Karl Küpfmüller published papers on a negative-feedback-based automatic gain control system and a feedback system stability criterion in 1928.[50]
Nyquist and Bode built on Black's work to develop a theory of amplifier stability.[49]
Early researchers in the area of cybernetics subsequently generalized the idea of negative feedback to cover any goal-seeking or purposeful behavior.[51]
All purposeful behavior may be considered to require negative feed-back. If a goal is to be attained, some signals from the goal are necessary at some time to direct the behavior.
Cybernetics pioneer Norbert Wiener helped to formalize the concepts of feedback control, defining feedback in general as "the chain of the transmission and return of information",[52] and negative feedback as the case when:
The information fed back to the control center tends to oppose the departure of the controlled from the controlling quantity...: 97
While the view of feedback as any "circularity of action" helped to keep the theory simple and consistent, Ashby pointed out that, while it may clash with definitions that require a "materially evident" connection, "the exact definition of feedback is nowhere important".[1] Ashby pointed out the limitations of the concept of "feedback":
The concept of 'feedback', so simple and natural in certain elementary cases, becomes artificial and of little use when the interconnections between the parts become more complex...Such complex systems cannot be treated as an interlaced set of more or less independent feedback circuits, but only as a whole. For understanding the general principles of dynamic systems, therefore, the concept of feedback is inadequate in itself. What is important is that complex systems, richly cross-connected internally, have complex behaviors, and that these behaviors can be goal-seeking in complex patterns.: 54
To reduce confusion, later authors have suggested alternative terms such as degenerative,[53] self-correcting,[54] balancing,[55] or discrepancy-reducing[56] in place of "negative".
See also
[edit]- Asymptotic gain model
- Biofeedback – Gaining awareness of biological processes
- Control theory – Branch of engineering and mathematics
- Cybernetics – Transdisciplinary field concerned with regulatory and purposive systems
- Climate change feedback – Feedback related to climate change
- Nyquist stability criterion – Graphical method of determining the stability of a dynamical system
- Open-loop controller – Control system whose input is independent of output
- Perceptual control theory – Psychological theory
- Positive feedback – Feedback loop that increases an initial small effect
- Stability criterion
- Step response – Time behavior of a system controlled by Heaviside step functions
References
[edit]- ^ a b c W. Ross Ashby (1957). "Chapter 12: The error-controlled regulator" (PDF). Introduction to cybernetics. Chapman & Hall Ltd.; Internet (1999). pp. 219–243.
- ^ Robert E. Ricklefs; Gary Leon Miller (2000). "§6.1 Homeostasis depends upon negative feedback". Ecology. Macmillan. p. 92. ISBN 9780716728290.
- ^ a b David A. Mindell (2002). Between Human and Machine : Feedback, Control, and Computing before Cybernetics. Baltimore, MD, USA: Johns Hopkins University Press. ISBN 9780801868955.
- ^ Arkalgud Ramaprasad (1983). "On The Definition of Feedback". Behavioral Science. 28 (1): 4–13. doi:10.1002/bs.3830280103.
- ^ John D.Sterman, Business Dynamics: Systems Thinking and Modeling for a Complex World McGraw Hill/Irwin, 2000. ISBN 9780072389159
- ^ Herold, David M.; Greller, Martin M. (1977). "Research Notes. Feedback: The Definition of a Construct". Academy of Management Journal. 20 (1): 142–147. JSTOR 255468.
- ^ Sudheer S Bhagade; Govind Das Nageshwar (2011). Process Dynamics and Control. PHI Learning Pvt. Ltd. pp. 6, 9. ISBN 9788120344051.
- ^
Charles H. Wilts (1960). Principles of Feedback Control. Addison-Wesley Pub. Co. p. 1.
In a simple feedback system a specific physical quantity is being controlled, and control is brought about by making an actual comparison of this quantity with its desired value and utilizing the difference to reduce the error observed. Such a system is self-correcting in the sense that any deviations from the desired performance are used to produce corrective action.
- ^ SK Singh (2010). Process Control: Concepts Dynamics And Applications. PHI Learning Pvt. Ltd. p. 222. ISBN 9788120336780.
- ^ For example, input and load disturbances. See William Y. Svrcek; Donald P. Mahoney; Brent R. Young (2013). A Real-Time Approach to Process Control (3rd ed.). John Wiley & Sons. p. 57. ISBN 9781118684733.
- ^ Charles D H Williams. "Types of feedback control". Feedback and temperature control. University of Exeter: Physics and astronomy. Retrieved 2014-06-08.
- ^ Giannini, Alessandra; Biasutti, Michela; Verstraete, Michel M. (2008-12-01). "A climate model-based review of drought in the Sahel: Desertification, the re-greening and climate change". Global and Planetary Change. Climate Change and Desertification. 64 (3): 119–128. Bibcode:2008GPC....64..119G. doi:10.1016/j.gloplacha.2008.05.004. ISSN 0921-8181.
- ^ Bechhoefer, John (2005). "Feedback for Physicists: A Tutorial Essay On Control". Reviews of Modern Physics. 77 (3): 783–835. Bibcode:2005RvMP...77..783B. CiteSeerX 10.1.1.124.7043. doi:10.1103/revmodphys.77.783.
- ^ Black, Harold (1937-12-21). "U.S. Patent 2,102,671: Wave Translation System" (PDF). www.eepatents.com. Archived from the original (PDF) on 2014-10-06.
- ^ a b James E Brittain (February 2011). "Electrical engineering hall of fame: Harold S Black" (PDF). Proceedings of the IEEE. 99 (2): 351–353. doi:10.1109/jproc.2010.2090997. Archived from the original (PDF) on November 29, 2014.
- ^ a b CA Desoer (August 1984). "In Memoriam: Harold Stephen Black". IEEE Transactions on Automatic Control. AC-29 (8): 673–674. doi:10.1109/tac.1984.1103645.
- ^ Santiram Kal (2009). "§6.3 Advantages of negative feedback amplifiers". Basic electronics: Devices, circuits and its fundamentals. PHI Learning Pvt. Ltd. pp. 193 ff. ISBN 9788120319523.
- ^ Marc Thomson (2006). "Figure 11-4: Classical single input, single output control loop". Intuitive Analog Circuit Design. Newnes. ISBN 9780080478753.
- ^ Santiram Kal (2009). "§6.3.1 Gain stability". Basic Electronics: Devices, Circuits, and IT Fundamentals. PHI Learning Pvt. Ltd. pp. 193–194. ISBN 9788120319523.
- ^ Marc T Thompson, p. 309
- ^ Thomas H Lee (2004). The Design of CMOS Radio Frequency Circuits (2nd ed.). Cambridge University Press. p. 447. ISBN 9780521835398.
- ^ Norbert A Malik (1995). "Improvement Factor". Electronic Circuits: Analysis simulation and design. Prentice Hall. p. 671. ISBN 9780023749100.
- ^ Santiram Kal (14 January 2009). "§6.3.2 Noise Reduction". Basic Electronics: Devices, Circuits and IT fundamentals. PHI Learning Pvt. p. 194. ISBN 9788120319523.
- ^ SK Bhattacharya. "§5.3.3 Effect of feedback on disturbance signal". Linear Control Systems: For Punjab Technical University. Pearson Education India. ISBN 9788131759523.
- ^ Muhammad Rashid (2010). Microelectronic Circuits: Analysis & Design (2nd ed.). Cengage Learning. p. 642. ISBN 9780495667728.
- ^
Wai-Kai Chen (2005). "Chapter 13: General feedback theory". Circuit Analysis and Feedback Amplifier Theory. CRC Press. pp. 13–1. ISBN 9781420037272.
[In a practical amplifier] the forward path may not be strictly unilateral, the feedback path is usually bilateral, and the input and output coupling networks are often complicated.
- ^ See, for example, Figure 1.4, p. 7 Ideal op amp model in Sergio Franco (2002). Design with operational amplifiers and analog integrated circuits (3rd ed.). McGraw-Hill. ISBN 978-0078028168. or David G Nair; Sergio B Franco (2009). "Figure 16.2: The four possible op-amp configurations". In Wai-Kai Chen (ed.). Fundamentals of Circuits and Filters (The Circuits and Filters Handbook, 3rd ed.). CRC Press. pp. 16–2. ISBN 9781420058888.
- ^ a b G. Schitter; A. Rankers (2014). "§6.3.4 Linear amplifiers with operational amplifiers". The Design of High Performance Mechatronics. IOS Press. p. 499. ISBN 9781614993681.
- ^ Walter G Jung (2005). "Noise gain (NG)". Op Amp Applications Handbook. Newnes. pp. 12 ff. ISBN 9780750678445.
- ^ Raven, PH; Johnson, GB. Biology, Fifth Edition, Boston: Hill Companies, Inc. 1999. page 1058.
- ^ William R. Uttal (2014). Psychomythics: Sources of Artifacts and Misconceptions in Scientific Psychology. Psychology Press. pp. 95 ff. ISBN 9781135623722.
- ^ Scott Camazine; Jean-Louis Deneubourg; Nigel R Franks; James Sneyd; Guy Theraulaz; Eric Bonabeau (2003). "Chapter 2: How self-organization works". Self-organization in biological systems. Princeton University Press. pp. 15 ff. ISBN 9780691116242.
- ^ Cybernetics: Or Control and Communication in the Animal and the Machine p.158
- ^ Goeroge Soros, The Alchemy of Finance
- ^ Herman Daly, Steady State Economics
- ^ "The Study of Earth as an Integrated System". nasa.gov. NASA. 2016. Archived from the original on November 2, 2016.
- ^ Fig. TS.17, Technical Summary, Sixth Assessment Report (AR6), Working Group I, IPCC, 2021, p. 96. Archived from the original on July 21, 2022.
- ^ Charlson, Robert J.; Lovelock, James E.; Andreae, Meinrat O.; Warren, Stephen G. (1987). "Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate". Nature. 326 (6114): 655–661. Bibcode:1987Natur.326..655C. doi:10.1038/326655a0. ISSN 1476-4687. S2CID 4321239.
- ^ Winton, Michael (2006). "Amplified Arctic climate change: What does surface albedo feedback have to do with it?". Geophysical Research Letters. 33 (3): L03701. Bibcode:2006GeoRL..33.3701W. doi:10.1029/2005GL025244. ISSN 1944-8007.
- ^ Stephens, Graeme L. (2005). "Cloud Feedbacks in the Climate System: A Critical Review". Journal of Climate. 18 (2): 237–273. Bibcode:2005JCli...18..237S. doi:10.1175/JCLI-3243.1. ISSN 0894-8755. S2CID 16122908.
- ^ Jickells, T. D.; An, Z. S.; Andersen, K. K.; Baker, A. R.; Bergametti, G.; Brooks, N.; Cao, J. J.; Boyd, P. W.; Duce, R. A.; Hunter, K. A.; Kawahata, H. (2005). "Global Iron Connections Between Desert Dust, Ocean Biogeochemistry, and Climate". Science. 308 (5718): 67–71. Bibcode:2005Sci...308...67J. doi:10.1126/science.1105959. ISSN 0036-8075. PMID 15802595. S2CID 16985005.
- ^ Giannini, Alessandra; Biasutti, Michela; Verstraete, Michel M. (2008). "A climate model-based review of drought in the Sahel: Desertification, the re-greening and climate change". Global and Planetary Change. Climate Change and Desertification. 64 (3): 119–128. Bibcode:2008GPC....64..119G. doi:10.1016/j.gloplacha.2008.05.004. ISSN 0921-8181.
- ^ Breedveld, Peter C (2004). "Port-based modeling of mechatronic systems". Mathematics and Computers in Simulation. 66 (2): 99–128. CiteSeerX 10.1.1.108.9830. doi:10.1016/j.matcom.2003.11.002.
- ^ "Tierie, Gerrit. Cornelis Drebbel. Amsterdam: HJ Paris, 1932" (PDF). Retrieved 2013-05-03.
- ^ Hills, Richard L (1996). Power From the Wind. Cambridge University Press. ISBN 9780521566865.
- ^ Maxwell, James Clerk (1868). "On Governors" (PDF). Proceedings of the Royal Society of London. 16: 270–283. doi:10.1098/rspl.1867.0055. S2CID 51751195 – via Wikimedia.
- ^ Friis, H. T.; Jensen, A. G. (1924). "High Frequency Amplifiers". Bell System Technical Journal. 3 (2): 181–205. doi:10.1002/j.1538-7305.1924.tb01354.x.
- ^ Black, H.S. (January 1934). "Stabilized Feedback Amplifiers" (PDF). Bell System Tech. J. 13 (1): 1–18. doi:10.1002/j.1538-7305.1934.tb00652.x. Retrieved January 2, 2013.
- ^ a b Stuart Bennett (1993). "Chapter 3: The electronic negative feedback amplifier". A history of control engineering 1930-1955. Institution of Electrical Engineers. pp. 70 ff. ISBN 9780863412806.
- ^ C. Bissell (2006). "Karl Kupfmuller, 1928: an early time-domain, closed-loop, stability criterion" (PDF). IEEE Control Systems Magazine: 115–116, 126.
- ^ Rosenblueth, Arturo, Norbert Wiener, and Julian Bigelow. "Behavior, purpose and teleology." Philosophy of science 10.1 (1943): 18-24.
- ^ Norbert Wiener Cybernetics: Or Control and Communication in the Animal and the Machine. Cambridge, Massachusetts: The Technology Press; New York: John Wiley & Sons, Inc., 1948.
- ^ Hermann A Haus and Richard B. Adler, Circuit Theory of Linear Noisy Networks, MIT Press, 1959
- ^ Peter M. Senge (1990). The Fifth Discipline: The Art and Practice of the Learning Organization. New York: Doubleday. p. 424. ISBN 978-0-385-26094-7.
- ^ Helen E. Allison; Richard J. Hobbs (2006). Science and Policy in Natural Resource Management: Understanding System Complexity. Cambridge University Press. p. 205. ISBN 9781139458603.
Balancing or negative feedback counteracts and opposes change
- ^ Carver, Charles S.; Scheier, Michael F. (2001-05-07). On the Self-Regulation of Behavior. Cambridge University Press. ISBN 9780521000994.
External links
[edit]- "Physiological Homeostasis". biology online: answers to your biology questions. Biology-Online.org. 30 January 2020.







