Octagon
| Regular octagon | |
|---|---|
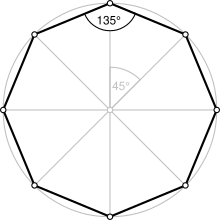 A regular octagon | |
| Type | Regular polygon |
| Edges and vertices | 8 |
| Schläfli symbol | {8}, t{4} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D8), order 2×8 |
| Internal angle (degrees) | 135° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, an octagon (from Ancient Greek ὀκτάγωνον (oktágōnon) 'eight angles') is an eight-sided polygon or 8-gon.
A regular octagon has Schläfli symbol {8} [1] and can also be constructed as a quasiregular truncated square, t{4}, which alternates two types of edges. A truncated octagon, t{8} is a hexadecagon, {16}. A 3D analog of the octagon can be the rhombicuboctahedron with the triangular faces on it like the replaced edges, if one considers the octagon to be a truncated square.
Properties
[edit]
The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°.
If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal (that is, whose diagonals are equal in length and at right angles to each other).[2]: Prop. 9
The midpoint octagon of a reference octagon has its eight vertices at the midpoints of the sides of the reference octagon. If squares are constructed all internally or all externally on the sides of the midpoint octagon, then the midpoints of the segments connecting the centers of opposite squares themselves form the vertices of a square.[2]: Prop. 10
Regularity
[edit]A regular octagon is a closed figure with sides of the same length and internal angles of the same size. It has eight lines of reflective symmetry and rotational symmetry of order 8. A regular octagon is represented by the Schläfli symbol {8}. The internal angle at each vertex of a regular octagon is 135° ( radians). The central angle is 45° ( radians).
Area
[edit]The area of a regular octagon of side length a is given by
In terms of the circumradius R, the area is
In terms of the apothem r (see also inscribed figure), the area is
These last two coefficients bracket the value of pi, the area of the unit circle.

The area can also be expressed as
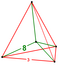
where S is the span of the octagon, or the second-shortest diagonal; and a is the length of one of the sides, or bases. This is easily proven if one takes an octagon, draws a square around the outside (making sure that four of the eight sides overlap with the four sides of the square) and then takes the corner triangles (these are 45–45–90 triangles) and places them with right angles pointed inward, forming a square. The edges of this square are each the length of the base.
Given the length of a side a, the span S is
The span, then, is equal to the silver ratio times the side, a.
The area is then as above:
Expressed in terms of the span, the area is
Another simple formula for the area is
More often the span S is known, and the length of the sides, a, is to be determined, as when cutting a square piece of material into a regular octagon. From the above,
The two end lengths e on each side (the leg lengths of the triangles (green in the image) truncated from the square), as well as being may be calculated as
Circumradius and inradius
[edit]The circumradius of the regular octagon in terms of the side length a is[3]
and the inradius is
(that is one-half the silver ratio times the side, a, or one-half the span, S)
The inradius can be calculated from the circumradius as
Diagonality
[edit]The regular octagon, in terms of the side length a, has three different types of diagonals:
- Short diagonal;
- Medium diagonal (also called span or height), which is twice the length of the inradius;
- Long diagonal, which is twice the length of the circumradius.
The formula for each of them follows from the basic principles of geometry. Here are the formulas for their length:[4]
- Short diagonal: ;
- Medium diagonal: ; (silver ratio times a)
- Long diagonal: .
Construction
[edit]
A regular octagon at a given circumcircle may be constructed as follows:
- Draw a circle and a diameter AOE, where O is the center and A, E are points on the circumcircle.
- Draw another diameter GOC, perpendicular to AOE.
- (Note in passing that A,C,E,G are vertices of a square).
- Draw the bisectors of the right angles GOA and EOG, making two more diameters HOD and FOB.
- A,B,C,D,E,F,G,H are the vertices of the octagon.
(The construction is very similar to that of hexadecagon at a given side length.)
A regular octagon can be constructed using a straightedge and a compass, as 8 = 23, a power of two:


The regular octagon can be constructed with meccano bars. Twelve bars of size 4, three bars of size 5 and two bars of size 6 are required.
Each side of a regular octagon subtends half a right angle at the centre of the circle which connects its vertices. Its area can thus be computed as the sum of eight isosceles triangles, leading to the result:
for an octagon of side a.
Standard coordinates
[edit]The coordinates for the vertices of a regular octagon centered at the origin and with side length 2 are:
- (±1, ±(1+√2))
- (±(1+√2), ±1).
Dissectibility
[edit]| 8-cube projection | 24 rhomb dissection | |
|---|---|---|

|
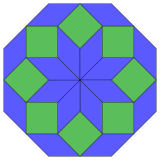 Regular |
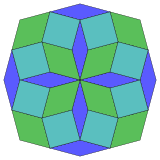 Isotoxal |

|

| |
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[5] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular octagon, m=4, and it can be divided into 6 rhombs, with one example shown below. This decomposition can be seen as 6 of 24 faces in a Petrie polygon projection plane of the tesseract. The list (sequence A006245 in the OEIS) defines the number of solutions as eight, by the eight orientations of this one dissection. These squares and rhombs are used in the Ammann–Beenker tilings.
 Tesseract |
 4 rhombs and 2 squares |
Skew
[edit]
A skew octagon is a skew polygon with eight vertices and edges but not existing on the same plane. The interior of such an octagon is not generally defined. A skew zig-zag octagon has vertices alternating between two parallel planes.
A regular skew octagon is vertex-transitive with equal edge lengths. In three dimensions it is a zig-zag skew octagon and can be seen in the vertices and side edges of a square antiprism with the same D4d, [2+,8] symmetry, order 16.
Petrie polygons
[edit]The regular skew octagon is the Petrie polygon for these higher-dimensional regular and uniform polytopes, shown in these skew orthogonal projections of in A7, B4, and D5 Coxeter planes.
| A7 | D5 | B4 | |
|---|---|---|---|
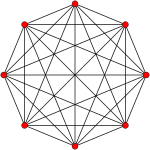 7-simplex |
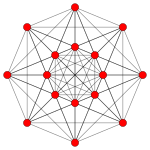 5-demicube |
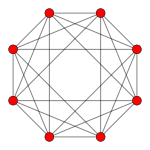 16-cell |
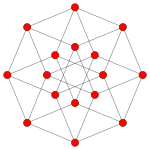 Tesseract |
Symmetry
[edit]The regular octagon has Dih8 symmetry, order 16. There are three dihedral subgroups: Dih4, Dih2, and Dih1, and four cyclic subgroups: Z8, Z4, Z2, and Z1, the last implying no symmetry.
 r16 | ||
|---|---|---|
 d8 |
 g8 |
 p8 |
d4 |
 g4 |
p4 |
 d2 |
 g2 |
p2 |
 a1 | ||
On the regular octagon, there are eleven distinct symmetries. John Conway labels full symmetry as r16.[6] The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars) Cyclic symmetries in the middle column are labeled as g for their central gyration orders. Full symmetry of the regular form is r16 and no symmetry is labeled a1.
The most common high symmetry octagons are p8, an isogonal octagon constructed by four mirrors can alternate long and short edges, and d8, an isotoxal octagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular octagon.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g8 subgroup has no degrees of freedom but can be seen as directed edges.
Use
[edit]
The octagonal shape is used as a design element in architecture. The Dome of the Rock has a characteristic octagonal plan. The Tower of the Winds in Athens is another example of an octagonal structure. The octagonal plan has also been in church architecture such as St. George's Cathedral, Addis Ababa, Basilica of San Vitale (in Ravenna, Italia), Castel del Monte (Apulia, Italia), Florence Baptistery, Zum Friedefürsten Church (Germany) and a number of octagonal churches in Norway. The central space in the Aachen Cathedral, the Carolingian Palatine Chapel, has a regular octagonal floorplan. Uses of octagons in churches also include lesser design elements, such as the octagonal apse of Nidaros Cathedral.
Architects such as John Andrews have used octagonal floor layouts in buildings for functionally separating office areas from building services, such as in the Intelsat Headquarters of Washington or Callam Offices in Canberra.
-
Umbrellas often have an octagonal outline.
-
The famous Bukhara rug design incorporates an octagonal "elephant's foot" motif.
-
Janggi uses octagonal pieces.
-
Japanese lottery machines often have octagonal shape.
-
Famous octagonal gold cup from the Belitung shipwreck
-
Classes at Shimer College are traditionally held around octagonal tables
-
The Labyrinth of the Reims Cathedral with a quasi-octagonal shape.
-
The movement of the analog stick(s) of the Nintendo 64 controller, the GameCube controller, the Wii Nunchuk and the Classic Controller is bounded by an octagonal frame, helping the user aim the stick in cardinal directions while still allowing circular freedom.
-
Chair from A la Ronde, with octagonal seats and backs (set of eight)
Derived figures
[edit]Related polytopes
[edit]The octagon, as a truncated square, is first in a sequence of truncated hypercubes:
| Image | 
|
 
|
 
|
 
|
 
|
|
 
|
... |
|---|---|---|---|---|---|---|---|---|
| Name | Octagon | Truncated cube | Truncated tesseract | Truncated 5-cube | Truncated 6-cube | Truncated 7-cube | Truncated 8-cube | |
| Coxeter diagram | ||||||||
| Vertex figure | ( )v( ) |  ( )v{ } |
 ( )v{3} |
 ( )v{3,3} |
( )v{3,3,3} | ( )v{3,3,3,3} | ( )v{3,3,3,3,3} |
As an expanded square, it is also first in a sequence of expanded hypercubes:

|
 
|
|
 
|
|
 
|
 
|
... |
| Octagon | Rhombicuboctahedron | Runcinated tesseract | Stericated 5-cube | Pentellated 6-cube | Hexicated 7-cube | Heptellated 8-cube | |
See also
[edit]- Bumper pool
- Hansen's small octagon
- Octagon house
- Octagonal number
- Octagram
- Octahedron, 3D shape with eight faces.
- Oktogon, a major intersection in Budapest, Hungary
- Rub el Hizb (also known as Al Quds Star and as Octa Star), a common motif in Islamic architecture
- Smoothed octagon
References
[edit]- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
- ^ a b Dao Thanh Oai (2015), "Equilateral triangles and Kiepert perspectors in complex numbers", Forum Geometricorum 15, 105--114. http://forumgeom.fau.edu/FG2015volume15/FG201509index.html Archived 2015-07-05 at the Wayback Machine
- ^ Weisstein, Eric. "Octagon." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Octagon.html
- ^ Alsina, Claudi; Nelsen, Roger B. (2023), A Panoply of Polygons, Dolciani Mathematical Expositions, vol. 58, American Mathematical Society, p. 124, ISBN 9781470471842
- ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
External links
[edit]- Octagon Calculator
- Definition and properties of an octagon With interactive animation








































