Trapezohedron
| Set of dual-uniform n-gonal trapezohedra | |
|---|---|
 Example: dual-uniform pentagonal trapezohedron (n = 5) | |
| Type | dual-uniform in the sense of dual-semiregular polyhedron |
| Faces | 2n congruent kites |
| Edges | 4n |
| Vertices | 2n + 2 |
| Vertex configuration | V3.3.3.n |
| Schläfli symbol | { } ⨁ {n}[1] |
| Conway notation | dAn |
| Coxeter diagram | |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | (convex) uniform n-gonal antiprism |
| Properties | convex, face-transitive, regular vertices[2] |
In geometry, an n-gonal trapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron[3],[4] is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites (sometimes also called trapezoids, or deltoids).[5]
The "n-gonal" part of the name does not refer to faces here, but to two arrangements of each n vertices around an axis of n-fold symmetry. The dual n-gonal antiprism has two actual n-gon faces.
An n-gonal trapezohedron can be dissected into two equal n-gonal pyramids and an n-gonal antiprism.
Terminology[edit]
These figures, sometimes called deltohedra,[3] must not be confused with deltahedra,[4] whose faces are equilateral triangles.
Twisted trigonal, tetragonal, and hexagonal trapezohedra (with six, eight, and twelve twisted congruent kite faces) exist as crystals; in crystallography (describing the crystal habits of minerals), they are just called trigonal, tetragonal, and hexagonal trapezohedra. They have no plane of symmetry, and no center of inversion symmetry;[6],[7] but they have a center of symmetry: the intersection point of their symmetry axes. The trigonal trapezohedron has one 3-fold symmetry axis, perpendicular to three 2-fold symmetry axes.[6] The tetragonal trapezohedron has one 4-fold symmetry axis, perpendicular to four 2-fold symmetry axes of two kinds. The hexagonal trapezohedron has one 6-fold symmetry axis, perpendicular to six 2-fold symmetry axes of two kinds.[8]
Crystal arrangements of atoms can repeat in space with trigonal and hexagonal trapezohedron cells.[9]
Also in crystallography, the word trapezohedron is often used for the polyhedron with 24 congruent non-twisted kite faces properly known as a deltoidal icositetrahedron,[10] which has eighteen order-4 vertices and eight order-3 vertices. This is not to be confused with the dodecagonal trapezohedron, which also has 24 congruent kite faces, but two order-12 apices (i.e. poles) and two rings of twelve order-3 vertices each.
Still in crystallography, the deltoid dodecahedron[11] has 12 congruent non-twisted kite faces, six order-4 vertices and eight order-3 vertices (the rhombic dodecahedron is a special case). This is not to be confused with the hexagonal trapezohedron, which also has 12 congruent kite faces,[8] but two order-6 apices (i.e. poles) and two rings of six order-3 vertices each.
Forms[edit]
An n-trapezohedron is defined by a regular zig-zag skew 2n-gon base, two symmetric apices with no degree of freedom right above and right below the base, and quadrilateral faces connecting each pair of adjacent basal edges to one apex.
An n-trapezohedron has two apical vertices on its polar axis, and 2n basal vertices in two regular n-gonal rings. It has 2n congruent kite faces, and it is isohedral.
| Trapezohedron name | Digonal trapezohedron (Tetrahedron) |
Trigonal trapezohedron | Tetragonal trapezohedron | Pentagonal trapezohedron | Hexagonal trapezohedron | Heptagonal trapezohedron | Octagonal trapezohedron | Decagonal trapezohedron | Dodecagonal trapezohedron | ... | Apeirogonal trapezohedron |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | 
|

|

|

|

|

|

|

|
... | ||
| Spherical tiling image | 
|

|

|

|

|

|

|

|

|
Plane tiling image | |
| Face configuration | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
Special cases:
- n = 2. A degenerate form of trapezohedron: a geometric tetrahedron with 6 vertices, 8 edges, and 4 degenerate kite faces that are degenerated into triangles. Its dual is a degenerate form of antiprism: also a tetrahedron.
- n = 3. The dual of a triangular antiprism: the kites are rhombi (or squares); hence these trapezohedra are also zonohedra. They are called rhombohedra. They are cubes scaled in the direction of a body diagonal. They are also the parallelepipeds with congruent rhombic faces.

A 60° rhombohedron, dissected into a central regular octahedron and two regular tetrahedra - A special case of a rhombohedron is one in which the rhombi forming the faces have angles of 60° and 120°. It can be decomposed into two equal regular tetrahedra and a regular octahedron. Since parallelepipeds can fill space, so can a combination of regular tetrahedra and regular octahedra.
- n = 5. The pentagonal trapezohedron is the only polyhedron other than the Platonic solids commonly used as a die in roleplaying games such as Dungeons & Dragons. Being convex and face-transitive, it makes fair dice. Having 10 sides, it can be used in repetition to generate any decimal-based uniform probability desired. Typically, two dice of different colors are used for the two digits to represent numbers from 00 to 99.
Symmetry[edit]
The symmetry group of an n-gonal trapezohedron is Dnd = Dnv, of order 4n, except in the case of n = 3: a cube has the larger symmetry group Od of order 48 = 4×(4×3), which has four versions of D3d as subgroups.
The rotation group of an n-trapezohedron is Dn, of order 2n, except in the case of n = 3: a cube has the larger rotation group O of order 24 = 4×(2×3), which has four versions of D3 as subgroups.
Note: Every n-trapezohedron with a regular zig-zag skew 2n-gon base and 2n congruent non-twisted kite faces has the same (dihedral) symmetry group as the dual-uniform n-trapezohedron, for n ≥ 4.
One degree of freedom within symmetry from Dnd (order 4n) to Dn (order 2n) changes the congruent kites into congruent quadrilaterals with three edge lengths, called twisted kites, and the n-trapezohedron is called a twisted trapezohedron. (In the limit, one edge of each quadrilateral goes to zero length, and the n-trapezohedron becomes an n-bipyramid.)
If the kites surrounding the two peaks are not twisted but are of two different shapes, the n-trapezohedron can only have Cnv (cyclic with vertical mirrors) symmetry, order 2n, and is called an unequal or asymmetric trapezohedron. Its dual is an unequal n-antiprism, with the top and bottom n-gons of different radii.
If the kites are twisted and are of two different shapes, the n-trapezohedron can only have Cn (cyclic) symmetry, order n, and is called an unequal twisted trapezohedron.
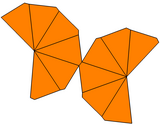
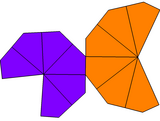
| Trapezohedron type | Twisted trapezohedron | Unequal trapezohedron | Unequal twisted trapezohedron | |
|---|---|---|---|---|
| Symmetry group | D6, (662), [6,2]+ | C6v, (*66), [6] | C6, (66), [6]+ | |
| Polyhedron image | 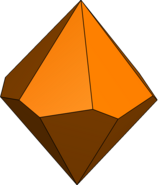
|

|

|

|
| Net | 
|
|
|

|
Star trapezohedron[edit]
A star p/q-trapezohedron (where 2 ≤ q < 1p) is defined by a regular zig-zag skew star 2p/q-gon base, two symmetric apices with no degree of freedom right above and right below the base, and quadrilateral faces connecting each pair of adjacent basal edges to one apex.
A star p/q-trapezohedron has two apical vertices on its polar axis, and 2p basal vertices in two regular p-gonal rings. It has 2p congruent kite faces, and it is isohedral.
Such a star p/q-trapezohedron is a self-intersecting, crossed, or non-convex form. It exists for any regular zig-zag skew star 2p/q-gon base (where 2 ≤ q < 1p).
But if p/q < 3/2, then (p − q)360°/p < q/2360°/p, so the dual star antiprism (of the star trapezohedron) cannot be uniform (i.e. cannot have equal edge lengths); and if p/q = 3/2, then (p − q)360°/p = q/2360°/p, so the dual star antiprism must be flat, thus degenerate, to be uniform.
A dual-uniform star p/q-trapezohedron has Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 5/2 | 5/3 | 7/2 | 7/3 | 7/4 | 8/3 | 8/5 | 9/2 | 9/4 | 9/5 |
|---|---|---|---|---|---|---|---|---|---|

|

|
||||||||
| 10/3 | 11/2 | 11/3 | 11/4 | 11/5 | 11/6 | 11/7 | 12/5 | 12/7 |
|---|---|---|---|---|---|---|---|---|
See also[edit]
- Diminished trapezohedron
- Rhombic dodecahedron
- Rhombic triacontahedron
- Bipyramid
- Truncated trapezohedron
- Conway polyhedron notation
- The Haunter of the Dark, a short story by H.P. Lovecraft in which a fictional ancient artifact known as The Shining Trapezohedron plays a crucial role.
References[edit]
- ^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c
- ^ "duality". maths.ac-noumea.nc. Retrieved 2020-10-19.
- ^ a b Weisstein, Eric W. "Trapezohedron". MathWorld. Retrieved 2024-04-24. Remarks: the faces of a deltohedron are deltoids; a (non-twisted) kite or deltoid can be dissected into two isosceles triangles or "deltas" (Δ), base-to-base.
- ^ a b Weisstein, Eric W. "Deltahedron". MathWorld. Retrieved 2024-04-28.
- ^ Spencer 1911, p. 575, or p. 597 on Wikisource, CRYSTALLOGRAPHY, 1. CUBIC SYSTEM, TETRAHEDRAL CLASS, footnote: « [Deltoid]: From the Greek letter δ, Δ; in general, a triangular-shaped object; also an alternative name for a trapezoid ». Remark: a twisted kite can look like and even be a trapezoid.
- ^ a b Spencer 1911, p. 581, or p. 603 on Wikisource, CRYSTALLOGRAPHY, 6. HEXAGONAL SYSTEM, Rhombohedral Division, TRAPEZOHEDRAL CLASS, FIG. 74.
- ^ Spencer 1911, p. 577, or p. 599 on Wikisource, CRYSTALLOGRAPHY, 2. TETRAGONAL SYSTEM, TRAPEZOHEDRAL CLASS.
- ^ a b Spencer 1911, p. 582, or p. 604 on Wikisource, CRYSTALLOGRAPHY, 6. HEXAGONAL SYSTEM, Hexagonal Division, TRAPEZOHEDRAL CLASS.
- ^ Trigonal-trapezohedric Class, 3 2 and Hexagonal-trapezohedric Class, 6 2 2
- ^ Spencer 1911, p. 574, or p. 596 on Wikisource, CRYSTALLOGRAPHY, 1. CUBIC SYSTEM, HOLOSYMMETRIC CLASS, FIG. 17.
- ^ Spencer 1911, p. 575, or p. 597 on Wikisource, CRYSTALLOGRAPHY, 1. CUBIC SYSTEM, TETRAHEDRAL CLASS, FIG. 27.
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms
- Spencer, Leonard James (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 07 (11th ed.). Cambridge University Press. pp. 569–591.
External links[edit]
- Weisstein, Eric W. "Trapezohedron". MathWorld.
- Weisstein, Eric W. "Isohedron". MathWorld.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML models (George Hart) <3> <4> <5> <6> <7> <8> [permanent dead link] <9> <10>
- Conway Notation for Polyhedra Try: "dAn", where n=3,4,5... Example: "dA5" is a pentagonal trapezohedron.
- Paper model tetragonal (square) trapezohedron

