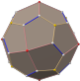
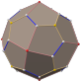
Deltoidal icositetrahedron
| Deltoidal icositetrahedron | |
|---|---|
 (rotating and 3D model) | |
| Type | Catalan |
| Conway notation | oC or deC |
| Coxeter diagram | |
| Face polygon |  Kite with 3 equal acute angles & 1 obtuse angle |
| Faces | 24, congruent |
| Edges | 24 short + 24 long = 48 |
| Vertices | 8 (connecting 3 short edges) + 6 (connecting 4 long edges) + 12 (connecting 4 alternate short & long edges) = 26 |
| Face configuration | V3.4.4.4 |
| Symmetry group | Oh, BC3, [4,3], *432 |
| Rotation group | O, [4,3]+, (432) |
| Dihedral angle | same value for short & long edges: |
| Dual polyhedron | Rhombicuboctahedron |
| Properties | convex, face-transitive |
 Net | |
In geometry, the deltoidal icositetrahedron (or trapezoidal icositetrahedron, tetragonal icosikaitetrahedron,[1] tetragonal trisoctahedron,[2] strombic icositetrahedron) is a Catalan solid. Its 24 faces are congruent kites.[3] The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other.
Cartesian coordinates[edit]
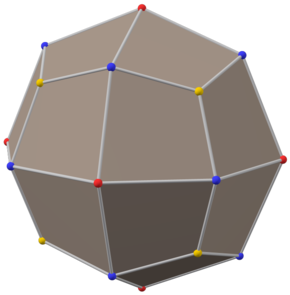
In the image above, the long body diagonals are those between opposite red vertices and between opposite blue vertices, and the short body diagonals are those between opposite yellow vertices.
Cartesian coordinates for the vertices of the deltoidal icositetrahedron centered at the origin and with long body diagonal length 2 are:
- red vertices (lying in -fold symmetry axes):
- blue vertices (lying in -fold symmetry axes):
- yellow vertices (lying in -fold symmetry axes):
For example, the point with coordinates is the intersection of the plane with equation and of the line with system of equations
A deltoidal icositetrahedron has three regular-octagon equators, lying in three orthogonal planes.
Dimensions and angles[edit]
Dimensions[edit]
The deltoidal icositetrahedron with long body diagonal length D = 2 has:
- short body diagonal length:
- long edge length:[4]
- short edge length:[4]
- inradius:[4]
is the distance from the center to any face plane; it may be calculated by normalizing the equation of plane above, replacing (x, y, z) with (0, 0, 0), and taking the absolute value of the result.
A deltoidal icositetrahedron has its long and short edges in the ratio:
The deltoidal icositetrahedron with short edge length has:
- area:[4]
- volume:[4]
Angles[edit]
For a deltoidal icositetrahedron, each kite face has:
- three equal acute angles, with value:
- one obtuse angle (between the short edges), with value:
Occurrences in nature and culture[edit]
The deltoidal icositetrahedron is a crystal habit often formed by the mineral analcime and occasionally garnet. The shape is often called a trapezohedron in mineral contexts, although in solid geometry the name trapezohedron has another meaning.
In Guardians of The Galaxy Vol. 3, the device containing the files about the experiments carried on Rocket Raccoon has the shape of a deitoidal icositetrahedron.
Orthogonal projections[edit]
The deltoidal icositetrahedron has three symmetry positions, all centered on vertices:
| Projective symmetry |
[2] | [4] | [6] |
|---|---|---|---|
| Image | 
|

|

|
| Dual image |

|

|

|
Related polyhedra[edit]
The deltoidal icositetrahedron's projection onto a cube divides its squares into quadrants. The projection onto a regular octahedron divides its equilateral triangles into kite faces. In Conway polyhedron notation this represents an ortho operation to a cube or octahedron.
The deltoidal icositetrahedron (dual of the small rhombicuboctahedron) is tightly related to the disdyakis dodecahedron (dual of the great rhombicuboctahedron). The main difference is that the latter also has edges between the vertices on 3- and 4-fold symmetry axes (between yellow and red vertices in the images below).

|

|

|

|
| Deltoidal icositetrahedron |
Disdyakis dodecahedron |
Dyakis dodecahedron |
Tetartoid |
Dyakis dodecahedron[edit]
A variant with pyritohedral symmetry is called a dyakis dodecahedron[5][6] or diploid.[7] It is common in crystallography.
A dyakis dodecahedron can be created by enlarging 24 of the 48 faces of a disdyakis dodecahedron. A tetartoid can be created by enlarging 12 of the 24 faces of a dyakis dodecahedron.

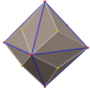
Stellation[edit]
The great triakis octahedron is a stellation of the deltoidal icositetrahedron.
Related polyhedra and tilings[edit]
The deltoidal icositetrahedron is a member of a family of duals to the uniform polyhedra related to the cube and regular octahedron.
When projected onto a sphere (see right), it can be seen that the edges make up the edges of a cube and regular octahedron arranged in their dual positions. It can also be seen that the 3- and 4-fold corners can be made to have the same distance to the center. In that case the resulting icositetrahedron will no longer have a rhombicuboctahedron for a dual, since the centers of the square and triangle faces of a rhombicuboctahedron are at different distances from its center.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
This polyhedron is a term of a sequence of topologically related deltoidal polyhedra with face configuration V3.4.n.4; this sequence continues with tilings of the Euclidean and hyperbolic planes. These face-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure Config. |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
See also[edit]
- Deltoidal hexecontahedron
- Tetrakis hexahedron, another 24-face Catalan solid which looks a bit like an overinflated cube.
- "The Haunter of the Dark", a story by H.P. Lovecraft, whose plot involves this figure.
- Pseudo-deltoidal icositetrahedron
References[edit]
- ^ Conway, Symmetries of Things, p. 284–286.
- ^ "Keyword: "forms" | ClipArt ETC".
- ^ "Kite". Retrieved 6 October 2019.
- ^ a b c d e Weisstein, Eric W. "Deltoidal Icositetrahedron". mathworld.wolfram.com. Retrieved 2022-10-06.
In this MathWorld entry, the small rhombicuboctahedron has edge length so this s.r.c.o.h. has circumradius and midradius so this s.r.c.o.h.'s dual with respect to their common midsphere is the deltoidal icositetrahedron with inradius ×× - ^ Isohedron 24k
- ^ The Isometric Crystal System
- ^ The 48 Special Crystal Forms
- ^ Both is indicated in the two crystal models in the top right corner of this photo. A visual demonstration can be seen here and here.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 23, Deltoidal icositetrahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal icosikaitetrahedron)
External links[edit]
- Weisstein, Eric W., "Deltoidal icositetrahedron" ("Catalan solid") at MathWorld.
- Deltoidal (Trapezoidal) Icositetrahedron – Interactive Polyhedron model