Truncated tetrahedron: Difference between revisions
Dedhert.Jr (talk | contribs) source |
Dedhert.Jr (talk | contribs) notes |
||
| Line 17: | Line 17: | ||
\end{align}</math> |
\end{align}</math> |
||
The dihedral angle of a truncated tetrahedron between triangle-to-hexagon is approximately 109.47°, and that between adjacent hexagonal faces is approximately 70.53°.{ |
The dihedral angle of a truncated tetrahedron between triangle-to-hexagon is approximately 109.47°, and that between adjacent hexagonal faces is approximately 70.53°.{{r|johnson}} |
||
The densest packing of the Archimedean truncated tetrahedron is believed to be <math display="inline"> \Phi = \frac{207}{208} </math>, as reported by two independent groups using [[Monte Carlo methods]] by {{harvtxt|Damasceno|Engel|Glotzer|2012}} and {{harvtxt|Jiao|Torquato|2013}}.{{r|damasceno|jiao}} Although no mathematical proof exists that this is the best possible packing for the truncated tetrahedron, the high proximity to the unity and independence of the findings make it unlikely that an even denser packing is to be found. In fact, if the truncation of the corners is slightly smaller than that of an Archimedean truncated tetrahedron, this new shape can be used to completely fill space.{{r|damasceno}} |
The densest packing of the Archimedean truncated tetrahedron is believed to be <math display="inline"> \Phi = \frac{207}{208} </math>, as reported by two independent groups using [[Monte Carlo methods]] by {{harvtxt|Damasceno|Engel|Glotzer|2012}} and {{harvtxt|Jiao|Torquato|2013}}.{{r|damasceno|jiao}} Although no mathematical proof exists that this is the best possible packing for the truncated tetrahedron, the high proximity to the unity and independence of the findings make it unlikely that an even denser packing is to be found. In fact, if the truncation of the corners is slightly smaller than that of an Archimedean truncated tetrahedron, this new shape can be used to completely fill space.{{r|damasceno}} |
||
| Line 139: | Line 139: | ||
| s2cid = 122006114 |
| s2cid = 122006114 |
||
| zbl = 0132.14603 | doi-access = free |
| zbl = 0132.14603 | doi-access = free |
||
}}</ref> |
}} See line II.</ref> |
||
<ref name="Williams">{{cite book |
<ref name="Williams">{{cite book |
||
Revision as of 02:06, 22 July 2024
This article or section is in a state of significant expansion or restructuring. You are welcome to assist in its construction by editing it as well. If this article or section has not been edited in several days, please remove this template. If you are the editor who added this template and you are actively editing, please be sure to replace this template with {{in use}} during the active editing session. Click on the link for template parameters to use.
This article was last edited by Dedhert.Jr (talk | contribs) 3 months ago. (Update timer) |
| Truncated tetrahedron | |
|---|---|
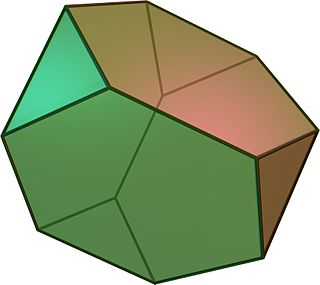 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 8, E = 18, V = 12 (χ = 2) |
| Faces by sides | 4{3}+4{6} |
| Conway notation | tT |
| Schläfli symbols | t{3,3} = h2{4,3} |
| t0,1{3,3} | |
| Wythoff symbol | 2 3 | 3 |
| Coxeter diagram | |
| Symmetry group | Td, A3, [3,3], (*332), order 24 |
| Rotation group | T, [3,3]+, (332), order 12 |
| Dihedral angle | 3-6: 109°28′16″ 6-6: 70°31′44″ |
| References | U02, C16, W6 |
| Properties | Semiregular convex |
 Colored faces |
 3.6.6 (Vertex figure) |
 Triakis tetrahedron (dual polyhedron) |
 Net |

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron at one third of the original edge length.
A truncated tetrahedron is the Goldberg polyhedron GIII(1,1), containing triangular and hexagonal faces.
A truncated tetrahedron can be called a cantic cube, with Coxeter diagram, ![]()
![]()
![]()
![]()
![]() , having half of the vertices of the cantellated cube (rhombicuboctahedron),
, having half of the vertices of the cantellated cube (rhombicuboctahedron), ![]()
![]()
![]()
![]()
![]() . There are two dual positions of this construction, and combining them creates the uniform compound of two truncated tetrahedra.
. There are two dual positions of this construction, and combining them creates the uniform compound of two truncated tetrahedra.
Properties
Given the edge length . The surface area of a truncated tetrahedron is the sum of 4 regular hexagons and 4 equilateral triangles' area, and its volume is:[1]
The dihedral angle of a truncated tetrahedron between triangle-to-hexagon is approximately 109.47°, and that between adjacent hexagonal faces is approximately 70.53°.[2]
The densest packing of the Archimedean truncated tetrahedron is believed to be , as reported by two independent groups using Monte Carlo methods by Damasceno, Engel & Glotzer (2012) and Jiao & Torquato (2013).[3][4] Although no mathematical proof exists that this is the best possible packing for the truncated tetrahedron, the high proximity to the unity and independence of the findings make it unlikely that an even denser packing is to be found. In fact, if the truncation of the corners is slightly smaller than that of an Archimedean truncated tetrahedron, this new shape can be used to completely fill space.[3]
The truncated tetrahedron is an Archimedean solid, meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex.[5] The truncated tetrahedron has the same three-dimensional group symmetry as the regular tetrahedron, the tetrahedral symmetry . The polygonal faces that meet for every vertex are one equilateral triangle and two regular hexagons, and the vertex figure is denoted as . Its dual polyhedron is triakis tetrahedron, a Catalan solid, shares the same symmetry as the truncated tetrahedron.[6]
Related polyhedrons
A lower symmetry version of the truncated tetrahedron (a truncated tetragonal disphenoid with order 8 D2d symmetry) is called a Friauf polyhedron in crystals such as complex metallic alloys. This form fits 5 Friauf polyhedra around an axis, giving a 72-degree dihedral angle on a subset of 6-6 edges.[citation needed] It is named after J. B. Friauf and his 1927 paper "The crystal structure of the intermetallic compound MgCu2".[7]
Appearances
Giant truncated tetrahedra were used for the "Man the Explorer" and "Man the Producer" theme pavilions in Expo 67. They were made of massive girders of steel bolted together in a geometric lattice. The truncated tetrahedra were interconnected with lattice steel platforms. All of these buildings were demolished after the end of Expo 67, as they had not been built to withstand the severity of the Montreal weather over the years. Their only remnants are in the Montreal city archives, the Public Archives Of Canada and the photo collections of tourists of the times.[8]
The Tetraminx puzzle has a truncated tetrahedral shape. This puzzle shows a dissection of a truncated tetrahedron into 4 octahedra and 6 tetrahedra. It contains 4 central planes of rotations.[citation needed]
Truncated tetrahedral graph
| Truncated tetrahedral graph | |
|---|---|
 3-fold symmetry | |
| Vertices | 12[9] |
| Edges | 18 |
| Radius | 3 |
| Diameter | 3[9] |
| Girth | 3[9] |
| Automorphisms | 24 (S4)[9] |
| Chromatic number | 3[9] |
| Chromatic index | 3[9] |
| Properties | Hamiltonian, regular, 3-vertex-connected, planar graph |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a truncated tetrahedral graph is an Archimedean graph, the graph of vertices and edges of the truncated tetrahedron, one of the Archimedean solids. It has 12 vertices and 18 edges.[10] It is a connected cubic graph,[11] and connected cubic transitive graph.[12]
| Circular |
|---|

|
| Orthographic projections | |
|---|---|
 4-fold symmetry |
 3-fold symmetry |
Examples
-
drawing in De divina proportione (1509)
-
drawing in Perspectiva Corporum Regularium (1568)
-
photos from different perspectives (Matemateca)
-
4-sided die
-
12 permutations of (brown)
See also
- Quarter cubic honeycomb – Fills space using truncated tetrahedra and smaller tetrahedra
- Truncated 5-cell – Similar uniform polytope in 4-dimensions
- Truncated triakis tetrahedron
- Triakis truncated tetrahedron
- Octahedron – a rectified tetrahedron
References
- ^ Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603. See line II.
- ^ a b Damasceno, Pablo F.; Engel, Michael; Glotzer, Sharon C. (2012). "Crystalline Assemblies and Densest Packings of a Family of Truncated Tetrahedra and the Role of Directional Entropic Forces". ACS Nano. 6 (2012): 609–614. arXiv:1109.1323. doi:10.1021/nn204012y. PMID 22098586. S2CID 12785227.
- ^ Jiao, Yang; Torquato, Sal (2011). "A Packing of Truncated Tetrahedra that Nearly Fills All of Space". arXiv:1107.2300 [cond-mat.soft].
- ^ Diudea, M. V. (2018). Multi-shell Polyhedral Clusters. Springer. p. 39. doi:10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
- ^ Cite error: The named reference
williamswas invoked but never defined (see the help page). - ^ Friauf, J. B. (1927). "The crystal structure of the intermetallic compound MgCu2". J. Am. Chem. Soc. 49: 3107–3114. doi:10.1021/ja01411a017.
- ^ "Expo 67 - Man the Producer - page 1".
- ^ a b c d e f An Atlas of Graphs, page=172, C105
- ^ An Atlas of Graphs, page 267, truncated tetrahedral graph
- ^ An Atlas of Graphs, page 130, connected cubic graphs, 12 vertices, C105
- ^ An Atlas of Graphs, page 161, connected cubic transitive graphs, 12 vertices, Ct11
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press
External links
- Weisstein, Eric W., "Truncated tetrahedron" ("Archimedean solid") at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra x3x3o - tut".
- Editable printable net of a truncated tetrahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra






























