Square
| Square | |
|---|---|
 A regular quadrilateral | |
| Type | Regular polygon |
| Edges and vertices | 4 |
| Schläfli symbol | {4} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D4), order 2×4 |
| Internal angle (degrees) | 90° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°). A square with vertices ABCD would be denoted ABCD.[1]
Characterizations
A quadrilateral is a square if and only if it is any one of the following:[2][3]
- A rectangle with two adjacent equal sides
- A rhombus with a right vertex angle
- A rhombus with all angles equal
- A parallelogram with one right vertex angle and two adjacent equal sides
- A quadrilateral with four equal sides and four right angles
- A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals)
- A convex quadrilateral with successive sides a, b, c, d whose area is [4]: Corollary 15
Properties
A square is a special case of a rhombus (equal sides, opposite equal angles), a kite (two pairs of adjacent equal sides), a trapezoid (one pair of opposite sides parallel), a parallelogram (all opposite sides parallel), a quadrilateral or tetragon (four-sided polygon), and a rectangle (opposite sides equal, right-angles), and therefore has all the properties of all these shapes, namely:[5]
- All four internal angles of a square are equal (each being 360°/4 = 90°, a right angle).
- The central angle of a square is equal to 90° (360°/4).
- The external angle of a square is equal to 90°.
- The diagonals of a square are equal and bisect each other, meeting at 90°.
- The diagonal of a square bisects its internal angle, forming adjacent angles of 45°.
- All four sides of a square are equal.
- Opposite sides of a square are parallel.
A square has Schläfli symbol {4}. A truncated square, t{4}, is an octagon, {8}. An alternated square, h{4}, is a digon, {2}. The square is the n = 2 case of the families of n-hypercubes and n-orthoplexes.
Perimeter and area

The perimeter of a square whose four sides have length is
and the area A is
Since four squared equals sixteen, a four by four square has an area equal to its perimeter. The only other quadrilateral with such a property is that of a three by six rectangle.
In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.
The area can also be calculated using the diagonal d according to
In terms of the circumradius R, the area of a square is
since the area of the circle is the square fills of its circumscribed circle.
In terms of the inradius r, the area of the square is
hence the area of the inscribed circle is of that of the square.
Because it is a regular polygon, a square is the quadrilateral of least perimeter enclosing a given area. Dually, a square is the quadrilateral containing the largest area within a given perimeter.[6] Indeed, if A and P are the area and perimeter enclosed by a quadrilateral, then the following isoperimetric inequality holds:
with equality if and only if the quadrilateral is a square.
Other facts
- The diagonals of a square are (about 1.414) times the length of a side of the square. This value, known as the square root of 2 or Pythagoras' constant,[1] was the first number proven to be irrational.
- A square can also be defined as a parallelogram with equal diagonals that bisect the angles.
- If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square.
- A square has a larger area than any other quadrilateral with the same perimeter.[7]
- A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).
- The square is in two families of polytopes in two dimensions: hypercube and the cross-polytope. The Schläfli symbol for the square is {4}.
- The square is a highly symmetric object. There are four lines of reflectional symmetry and it has rotational symmetry of order 4 (through 90°, 180° and 270°). Its symmetry group is the dihedral group D4.
- A square can be inscribed inside any regular polygon. The only other polygon with this property is the equilateral triangle.
- If the inscribed circle of a square ABCD has tangency points E on AB, F on BC, G on CD, and H on DA, then for any point P on the inscribed circle,[8]
- If is the distance from an arbitrary point in the plane to the i-th vertex of a square and is the circumradius of the square, then[9]
- If and are the distances from an arbitrary point in the plane to the centroid of the square and its four vertices respectively, then [10]
- and
- where is the circumradius of the square.
Coordinates and equations

The coordinates for the vertices of a square with vertical and horizontal sides, centered at the origin and with side length 2 are (±1, ±1), while the interior of this square consists of all points (xi, yi) with −1 < xi < 1 and −1 < yi < 1. The equation
specifies the boundary of this square. This equation means "x2 or y2, whichever is larger, equals 1." The circumradius of this square (the radius of a circle drawn through the square's vertices) is half the square's diagonal, and is equal to Then the circumcircle has the equation
Alternatively the equation
can also be used to describe the boundary of a square with center coordinates (a, b), and a horizontal or vertical radius of r. The square is therefore the shape of a topological ball according to the L1 distance metric.
Construction
The following animations show how to construct a square using a compass and straightedge. This is possible as 4 = 22, a power of two.
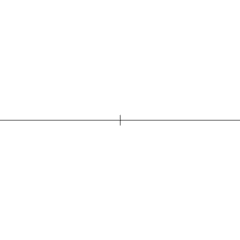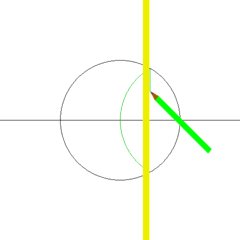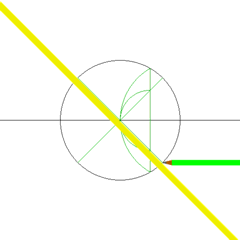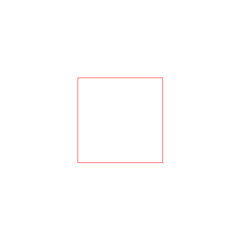
right angle by using Thales' theorem
Symmetry
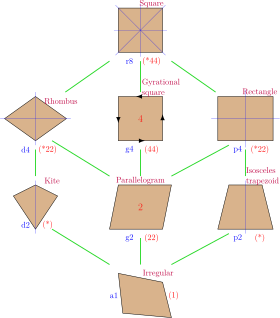
The square has Dih4 symmetry, order 8. There are 2 dihedral subgroups: Dih2, Dih1, and 3 cyclic subgroups: Z4, Z2, and Z1.
A square is a special case of many lower symmetry quadrilaterals:
- A rectangle with two adjacent equal sides
- A quadrilateral with four equal sides and four right angles
- A parallelogram with one right angle and two adjacent equal sides
- A rhombus with a right angle
- A rhombus with all angles equal
- A rhombus with equal diagonals
These 6 symmetries express 8 distinct symmetries on a square. John Conway labels these by a letter and group order.[11]
Each subgroup symmetry allows one or more degrees of freedom for irregular quadrilaterals. r8 is full symmetry of the square, and a1 is no symmetry. d4 is the symmetry of a rectangle, and p4 is the symmetry of a rhombus. These two forms are duals of each other, and have half the symmetry order of the square. d2 is the symmetry of an isosceles trapezoid, and p2 is the symmetry of a kite. g2 defines the geometry of a parallelogram.
Only the g4 subgroup has no degrees of freedom, but can be seen as a square with directed edges.
Squares inscribed in triangles
Every acute triangle has three inscribed squares (squares in its interior such that all four of a square's vertices lie on a side of the triangle, so two of them lie on the same side and hence one side of the square coincides with part of a side of the triangle). In a right triangle two of the squares coincide and have a vertex at the triangle's right angle, so a right triangle has only two distinct inscribed squares. An obtuse triangle has only one inscribed square, with a side coinciding with part of the triangle's longest side.
The fraction of the triangle's area that is filled by the square is no more than 1/2.
Squaring the circle
Squaring the circle, proposed by ancient geometers, is the problem of constructing a square with the same area as a given circle, by using only a finite number of steps with compass and straightedge.
In 1882, the task was proven to be impossible as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental number rather than an algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients.
Non-Euclidean geometry
In non-Euclidean geometry, squares are more generally polygons with 4 equal sides and equal angles.
In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of plane geometry, the angles of such a square are larger than a right angle. Larger spherical squares have larger angles.
In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have angles of less than right angles. Larger hyperbolic squares have smaller angles.
Examples:
 Two squares can tile the sphere with 2 squares around each vertex and 180-degree internal angles. Each square covers an entire hemisphere and their vertices lie along a great circle. This is called a spherical square dihedron. The Schläfli symbol is {4,2}. |
 Six squares can tile the sphere with 3 squares around each vertex and 120-degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}. |
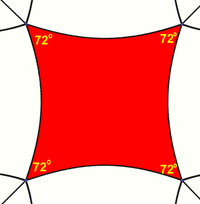 Squares can tile the hyperbolic plane with 5 around each vertex, with each square having 72-degree internal angles. The Schläfli symbol is {4,5}. In fact, for any n ≥ 5 there is a hyperbolic tiling with n squares about each vertex. |
Crossed square

A crossed square is a faceting of the square, a self-intersecting polygon created by removing two opposite edges of a square and reconnecting by its two diagonals. It has half the symmetry of the square, Dih2, order 4. It has the same vertex arrangement as the square, and is vertex-transitive. It appears as two 45-45-90 triangles with a common vertex, but the geometric intersection is not considered a vertex.
A crossed square is sometimes likened to a bow tie or butterfly. the crossed rectangle is related, as a faceting of the rectangle, both special cases of crossed quadrilaterals.[12]
The interior of a crossed square can have a polygon density of ±1 in each triangle, dependent upon the winding orientation as clockwise or counterclockwise.
A square and a crossed square have the following properties in common:
- Opposite sides are equal in length.
- The two diagonals are equal in length.
- It has two lines of reflectional symmetry and rotational symmetry of order 2 (through 180°).
It exists in the vertex figure of a uniform star polyhedra, the tetrahemihexahedron.
Graphs

The K4 complete graph is often drawn as a square with all 6 possible edges connected, hence appearing as a square with both diagonals drawn. This graph also represents an orthographic projection of the 4 vertices and 6 edges of the regular 3-simplex (tetrahedron).
See also
- Cube
- Pythagorean theorem
- Square lattice
- Square number
- Square root
- Squaring the square
- Squircle
- Unit square
References
- ^ a b c Weisstein, Eric W. "Square". Wolfram MathWorld. Retrieved 2020-09-02.
- ^ Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, p. 59, ISBN 1-59311-695-0.
- ^ "Problem Set 1.3". jwilson.coe.uga.edu. Retrieved 2017-12-12.
- ^ Josefsson, Martin, "Properties of equidiagonal quadrilaterals" Archived 2022-09-27 at the Wayback Machine Forum Geometricorum, 14 (2014), 129–144.
- ^ "Quadrilaterals - Square, Rectangle, Rhombus, Trapezoid, Parallelogram". www.mathsisfun.com. Retrieved 2020-09-02.
- ^ Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ^ Lundsgaard Hansen, Martin. "Vagn Lundsgaard Hansen". www2.mat.dtu.dk. Retrieved 2017-12-12.
- ^ "Geometry classes, Problem 331. Square, Point on the Inscribed Circle, Tangency Points. Math teacher Master Degree. College, SAT Prep. Elearning, Online math tutor, LMS". gogeometry.com. Retrieved 2017-12-12.
- ^ Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227–232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf Archived 2016-10-10 at the Wayback Machine
- ^ Meskhishvili, Mamuka (2021). "Cyclic Averages of Regular Polygonal Distances" (PDF). International Journal of Geometry. 10: 58–65.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275–278)
- ^ Wells, Christopher J. "Quadrilaterals". www.technologyuk.net. Retrieved 2017-12-12.
External links
- Animated course (Construction, Circumference, Area)
- Definition and properties of a square With interactive applet
- Animated applet illustrating the area of a square



























