Prism (geometry)

Template:Other uses2

Set of uniform prisms
(A hexagonal prism is shown)
Type	uniform polyhedron
Conway polyhedron notation	Pn
Faces	2+n total: 2 {n} n {4}
Edges	3n
Vertices	2n
Schläfli symbol	{n}×{} or t{2, n}
Coxeter diagram
Vertex configuration	4.4.n
Symmetry group	D_nh, [n,2], (*n22), order 4n
Rotation group	D_n, [n,2]⁺, (n22), order 2n
Dual polyhedron	bipyramids
Properties	convex, semi-regular vertex-transitive
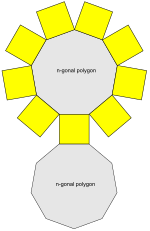n-gonal prism net (n = 9 here)

In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.

General, right and uniform prisms

A right prism is a prism in which the joining edges and faces are perpendicular to the base faces.^[1] This applies if the joining faces are rectangular. If the joining edges and faces are not perpendicular to the base faces, it is called an oblique prism.

For example a parallelepiped is an oblique prism of which the base is a parallelogram, or equivalently a polyhedron with six faces which are all parallelograms.

A truncated triangular prism with its top face truncated at an oblique angle

A truncated prism is a prism with nonparallel top and bottom faces.^[2]

Some texts may apply the term rectangular prism or square prism to both a right rectangular-sided prism and a right square-sided prism. A right p-gonal prism with rectangular sides has a Schläfli symbol { } × {p}.

A right rectangular prism is also called a cuboid, or informally a rectangular box. A right square prism is simply a square box, and may also be called a square cuboid. A right rectangular prism has Schläfli symbol { }×{ }×{ }.

An n-prism, having regular polygon ends and rectangular sides, approaches a cylindrical solid as n approaches infinity.

The term uniform prism or semiregular prism can be used for a right prism with square sides, since such prisms are in the set of uniform polyhedra. A uniform p-gonal prism has a Schläfli symbol t{2,p}. Right prisms with regular bases and equal edge lengths form one of the two infinite series of semiregular polyhedra, the other series being the antiprisms.

The dual of a right prism is a bipyramid.

Volume

The volume of a prism is the product of the area of the base and the distance between the two base faces, or the height (in the case of a non-right prism, note that this means the perpendicular distance).

The volume is therefore:

V=B\cdot h

where B is the base area and h is the height. The volume of a prism whose base is a regular n-sided polygon with side length s is therefore:

V={\frac {n}{4}}hs^{2}\cot {\frac {\pi }{n}}.

Surface area

The surface area of a right prism is 2 · B + P · h, where B is the area of the base, h the height, and P the base perimeter.

The surface area of a right prism whose base is a regular n-sided polygon with side length s and height h is therefore:

A={\frac {n}{2}}s^{2}\cot {\frac {\pi }{n}}+nsh.

Schlegel diagrams

P3	P4	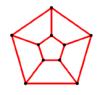P5	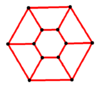P6	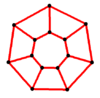P7	P8

Symmetry

The symmetry group of a right n-sided prism with regular base is D_nh of order 4n, except in the case of a cube, which has the larger symmetry group O_h of order 48, which has three versions of D_4h as subgroups. The rotation group is D_n of order 2n, except in the case of a cube, which has the larger symmetry group O of order 24, which has three versions of D₄ as subgroups.

The symmetry group D_nh contains inversion iff n is even.

Prismatic polytope

A prismatic polytope is a higher-dimensional generalization of a prism. An n-dimensional prismatic polytope is constructed from two (n − 1)-dimensional polytopes, translated into the next dimension.

The prismatic n-polytope elements are doubled from the (n − 1)-polytope elements and then creating new elements from the next lower element.

Take an n-polytope with f_i i-face elements (i = 0, ..., n). Its (n + 1)-polytope prism will have 2f_i + f_i−1 i-face elements. (With f₋₁ = 0, f_n = 1.)

By dimension:

Take a polygon with n vertices, n edges. Its prism has 2n vertices, 3n edges, and 2 + n faces.
Take a polyhedron with v vertices, e edges, and f faces. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2 + f cells.
Take a polychoron with v vertices, e edges, f faces and c cells. Its prism has 2v vertices, 2e + v edges, 2f + e faces, and 2c + f cells, and 2 + c hypercells.

Uniform prismatic polytope

A regular n-polytope represented by Schläfli symbol {p, q, ..., t} can form a uniform prismatic (n + 1)-polytope represented by a Cartesian product of two Schläfli symbols: {p, q, ..., t}×{}.

By dimension:

A 0-polytopic prism is a line segment, represented by an empty Schläfli symbol {}.
A 1-polytopic prism is a rectangle, made from 2 translated line segments. It is represented as the product Schläfli symbol {}×{}. If it is square, symmetry can be reduced: {}×{} = {4}.
- Example: Square, {}×{}, two parallel line segments, connected by two line segment sides.
A polygonal prism is a 3-dimensional prism made from two translated polygons connected by rectangles. A regular polygon {p} can construct a uniform n-gonal prism represented by the product {p}×{}. If p = 4, with square sides symmetry it becomes a cube: {4}×{} = {4, 3}.
- Example: Pentagonal prism, {5}×{}, two parallel pentagons connected by 5 rectangular sides.
A polyhedral prism is a 4-dimensional prism made from two translated polyhedra connected by 3-dimensional prism cells. A regular polyhedron {p, q} can construct the uniform polychoric prism, represented by the product {p, q}×{}. If the polyhedron is a cube, and the sides are cubes, it becomes a tesseract: {4, 3}×{} = {4, 3, 3}.
- Example: Dodecahedral prism, {5, 3}×{}, two parallel dodecahedra connected by 12 pentagonal prism sides.
...

Higher order prismatic polytopes also exist as cartesian products of any two polytopes. The dimension of a polytope is the product of the dimensions of the elements. The first example of these exist in 4-dimensional space are called duoprisms as the product of two polygons. Regular duoprisms are represented as {p}×{q}.

Family of uniform n-gonal prisms v t e
Prism name	Digonal prism	(Trigonal) Triangular prism	(Tetragonal) Square prism	Pentagonal prism	Hexagonal prism	Heptagonal prism	Octagonal prism	Enneagonal prism	Decagonal prism	Hendecagonal prism	Dodecagonal prism	...	Apeirogonal prism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Twisted prism

A twisted prism is a nonconvex prism polyhedron constructed by a uniform q-prism with the side faces bisected on the square diagonal, and twisting the top, usually by 180/q degrees in the same direction, causing side triangles to be concave.^[3]^[4]

A twisted prism cannot be triangulated into tetrahedra without adding new vertices. The smallest case, triangular form, is called a Schönhardt polyhedron.

A twisted prism is topologically identical to the antiprism, but has half the symmetry: D_n, [n,2]⁺, order 2n. It can be seen as a convex antiprism, with tetrahedra removed between pairs of triangles.

3-gonal	4-gonal		12-gonal
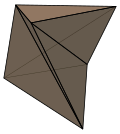Schönhardt polyhedron	Twisted square prism	Square antiprism	Twisted dodecagonal antiprism

.

Related polyhedra and tilings

Family of uniform n-gonal prisms v t e
Prism name	Digonal prism	(Trigonal) Triangular prism	(Tetragonal) Square prism	Pentagonal prism	Hexagonal prism	Heptagonal prism	Octagonal prism	Enneagonal prism	Decagonal prism	Hendecagonal prism	Dodecagonal prism	...	Apeirogonal prism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Family of convex cupolae
v
t
e
n	2	3	4	5	6	7	8
Schläfli symbol	${2} \|\| t{2}$	${3} \|\| t{3}$	${4} \|\| t{4}$	${5} \|\| t{5}$	${6} \|\| t{6}$	${7} \|\| t{7}$	${8} \|\| t{8}$
Cupola	Digonal cupola	Triangular cupola	Square cupola	Pentagonal cupola	Hexagonal cupola (Flat)	Heptagonal cupola (Non-regular face)	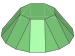Octagonal cupola (Non-regular face)
Related uniform polyhedra	Rhombohedron	Cuboctahedron	Rhombicuboctahedron	Rhombicosidodecahedron	Rhombitrihexagonal tiling	Rhombitriheptagonal tiling	Rhombitrioctagonal tiling

Symmetry mutations

This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.

*n32 symmetry mutation of truncated tilings: t{n,3} v t e
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Symmetry *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Symbol	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Triakis figures
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

*n32 symmetry mutation of expanded tilings: 3.4.n.4
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paracomp.
Symmetry *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Compounds

There are 4 uniform compounds of triangular prisms:

Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.

Honeycombs

There are 9 uniform honeycombs that include triangular prism cells:

Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb

Related polytopes

The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −1₂₁.

k₂₁ figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
E_n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	1,920	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	−1₂₁	0₂₁	1₂₁	2₂₁	3₂₁	4₂₁	5₂₁	6₂₁

Four dimensional space

The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:

References

^ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.28
^ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.81
^ The facts on file: Geometry handbook, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4, p.172
^ [1]

Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisma and antiprisms

External links

Weisstein, Eric W. "Prism". MathWorld.
Olshevsky, George. "Prismatic polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
Nonconvex Prisms and Antiprisms
Surface Area MATHguide
Volume MATHguide
Paper models of prisms and antiprisms Free nets of prisms and antiprisms
Paper models of prisms and antiprisms Using nets generated by Stella.
Stella: Polyhedron Navigator: Software used to create the 3D and 4D images on this page.

[1] William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.28

[2] William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.81

[3] The facts on file: Geometry handbook, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4, p.172

[4] [1]

[1]

[2]

[3]

[4]

tetrahedral prism	octahedral prism	cuboctahedral prism	icosahedral prism	icosidodecahedral prism	Truncated dodecahedral prism

Rhombi-cosidodecahedral prism	Rhombi-cuboctahedral prism	Truncated cubic prism	Snub dodecahedral prism	n-gonal antiprismatic prism

Cantellated 5-cell	Cantitruncated 5-cell	Runcinated 5-cell	Runcitruncated 5-cell	Cantellated tesseract	Cantitruncated tesseract	Runcinated tesseract	Runcitruncated tesseract

Cantellated 24-cell	Cantitruncated 24-cell	Runcinated 24-cell	Runcitruncated 24-cell	Cantellated 120-cell	Cantitruncated 120-cell	Runcinated 120-cell	Runcitruncated 120-cell