Radial velocity

"Radial speed" redirects here. Not to be confused with radial motion.

A plane flying past a radar station: the plane's velocity vector (red) is the sum of the radial velocity (green) and the tangential velocity (blue).

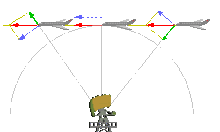
The radial velocity of an object with respect to a given point is the rate of change of the distance between the object and the point. That is, the radial velocity is the component of the object's velocity that points in the direction of the radius connecting the object and the point. In astronomy, the point is usually taken to be the observer on Earth, so the radial velocity then denotes the speed with which the object moves away from or approaches the Earth.

In astronomy, radial velocity most commonly refers to the spectroscopic radial velocity, which is determined by spectroscopy. i.e. by measuring the frequencies of light received from the object. By contrast, astrometric radial velocity is determined by astrometric observations (for example, a secular change in the annual parallax).

Spectroscopic radial velocity

Light from an object with a substantial relative radial velocity at emission will be subject to the Doppler effect, so the frequency of the light decreases for objects that were receding (redshift) and increases for objects that were approaching (blueshift).

The radial velocity of a star or other luminous distant objects can be measured accurately by taking a high-resolution spectrum and comparing the measured wavelengths of known spectral lines to wavelengths from laboratory measurements. A positive radial velocity indicates the distance between the objects is or was increasing; a negative radial velocity indicates the distance between the source and observer is or was decreasing.

Diagram showing how an exoplanet's orbit changes the position and velocity of a star as they orbit a common center of mass.

In many binary stars, the orbital motion usually causes radial velocity variations of several kilometers per second (km/s). As the spectra of these stars vary due to the Doppler effect, they are called spectroscopic binaries. Radial velocity can be used to estimate the ratio of the masses of the stars, and some orbital elements, such as eccentricity and semimajor axis. The same method has also been used to detect planets around stars, in the way that the movement's measurement determines the planet's orbital period, while the resulting radial-velocity amplitude allows the calculation of the lower bound on a planet's mass using the binary mass function. Radial velocity methods alone may only reveal a lower bound, since a large planet orbiting at a very high angle to the line of sight will perturb its star radially as much as a much smaller planet with an orbital plane on the line of sight. It has been suggested that planets with high eccentricities calculated by this method may in fact be two-planet systems of circular or near-circular resonant orbit.

Detection of exoplanets

Main article: Doppler spectroscopy

The radial velocity method to detect exoplanets

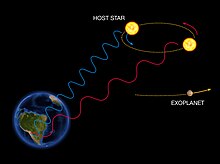
The radial velocity method to detect exoplanets is based on the detection of variations in the velocity of the central star, due to the changing direction of the gravitational pull from an (unseen) exoplanet as it orbits the star. When the star moves towards us, its spectrum is blueshifted, while it is redshifted when it moves away from us. By regularly looking at the spectrum of a star – and so, measuring its velocity – one can see if it moves periodically due to the influence of a companion.

Data reduction

From the instrumental perspective, velocities are measured relative to the telescope's motion. So an important first step of the data reduction is to remove the contributions of

- the Earth's elliptic motion around the sun at approximately ± 30 km/s,

- a monthly rotation of ± 12 m/s of the Earth around the center of gravity of the Earth-Moon system,

- the daily rotation of the telescope with the Earth crust around the Earth axis, which is up to 400 m/s at the equator and proportional to the cosine of the telescope's latitude,

- small contributions from the Earth polar motion,

- contributions of 220 km/s from the motion around the Galactic center and associated proper motions.

See also

• Proper motion
• Peculiar velocity
• Relative velocity

References

• The Radial Velocity Equation in the Search for Exoplanets ( The Doppler Spectroscopy or Wobble Method )