Centered octagonal number

A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers. The centered octagonal number for n is given by the formula

$8T_{n-1}+1$

where T is a regular triangular number, or much more simply, by squaring the odd numbers:

$(2n-1)^2 = 4n^2-4n+1.$

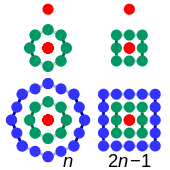
The first few centered octagonal numbers are

1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089

All centered octagonal numbers are odd, and in base 10 one can notice the one's digits follow the pattern 1-9-5-9-1. An odd number is a centered octagonal number if and only if it is a perfect square.

Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number.

See also regular octagonal number.