Steinmetz solid

Steinmetz solid (intersection of two cylinders)

In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse.

The intersection of two cylinders is called a bicylinder. Topologically, it is equivalent to a square hosohedron. The intersection of three cylinders is called a tricylinder. A bisected bicylinder is called a vault, and a cloister vault in architecture has this shape.

Steinmetz solids are named after mathematician Charles Proteus Steinmetz, who solved the problem of determining the volume of the intersection. However, the same problem had been solved earlier, by Archimedes in the ancient Greek world, Zu Chongzhi in ancient China, and Piero della Francesca in the early Italian Renaissance. They appear prominently in the sculptures of Frank Smullin.

Animated depiction of a bicylinder

Bicylinder

The generation of a bicylinder

Calculating the volume of a bicylinder

A bicylinder generated by two cylinders with radius r has the volume $$V={\frac {16}{3}}r^{3},$$ and the surface area $$A=16r^{2}.$$

The upper half of a bicylinder is the square case of a domical vault, a dome-shaped solid based on any convex polygon whose cross-sections are similar copies of the polygon, and analogous formulas calculating the volume and surface area of a domical vault as a rational multiple of the volume and surface area of its enclosing prism hold more generally. In China, the bicylinder is known as Mou he fang gai, literally "two square umbrella"; it was described by the third-century mathematician Liu Hui.

Proof of the volume formula

For deriving the volume formula it is convenient to use the common idea for calculating the volume of a sphere: collecting thin cylindric slices. In this case the thin slices are square cuboids (see diagram). This leads to $${\begin{aligned}V&=\int _{-r}^{r}(2x)^{2}\ \mathrm {d} z\\[2pt]&=4\cdot \int _{-r}^{r}x^{2}\ \mathrm {d} z\\[2pt]&=4\cdot \int _{-r}^{r}(r^{2}-z^{2})\ \mathrm {d} z\\[2pt]&={\frac {16}{3}}r^{3}.\end{aligned}}$$ It is well known that the relations of the volumes of a right circular cone, one half of a sphere and a right circular cylinder with same radii and heights are 1 : 2 : 3. For one half of a bicylinder a similar statement is true:

• The relations of the volumes of the inscribed square pyramid $(a=2r,\ h=r,\ V={\tfrac {4}{3}}r^{3}),$ the half bicylinder $(V={\tfrac {8}{3}}r^{3})$ and the surrounding squared cuboid $(a=2r,\ h=r,\ V=4r^{3})$ are 1 : 2 : 3:$${\begin{array}{ccccc}{\frac {4}{3}}r^{3}&:&{\frac {8}{3}}r^{3}&:&4r^{3}\\[2pt]1&:&2&:&3\end{array}}$$

Using Multivariable Calculus

Consider the equations of the cylinders:

$${\begin{aligned}x^{2}+z^{2}&=r^{2}\\x^{2}+y^{2}&=r^{2}\end{aligned}}$$

The volume will be given by:

$$V=\iiint _{V}\mathrm {d} z\,\mathrm {d} y\,\mathrm {d} x$$

With the limits of integration:

$${\begin{array}{rcccl}-{\sqrt {r^{2}-x^{2}}}&\leqslant &z&\leqslant &{\sqrt {r^{2}-x^{2}}}\\[4pt]-{\sqrt {r^{2}-x^{2}}}&\leqslant &y&\leqslant &{\sqrt {r^{2}-x^{2}}}\\[4pt]-r&\leqslant &x&\leqslant &r\end{array}}$$

Substituting, we have:

$${\begin{aligned}V&=\int _{-r}^{r}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\mathrm {d} z\,\mathrm {d} y\,\mathrm {d} x\\[2pt]&=8r^{3}-{\frac {8r^{3}}{3}}\\[2pt]&={\frac {16r^{3}}{3}}\end{aligned}}$$

Proof of the area formula

The surface area consists of two red and two blue cylindrical biangles. One red biangle is cut into halves by the yz-plane and developed into the plane such that half circle (intersection with the yz-plane) is developed onto the positive ξ-axis and the development of the biangle is bounded upwards by the sine arc $\eta =r\sin {\tfrac {\xi }{r}},\ 0\leq \xi \leq \pi r.$ Hence the area of this development is

cloister vault

$$B=\int _{0}^{\pi r}r\sin {\frac {\xi }{r}}\ \mathrm {d} \xi =r^{2}\cos {0}-r^{2}\cos {\pi }=2r^{2}$$ and the total surface area is: $$A=8B=16r^{2}.$$

Alternate proof of the volume formula

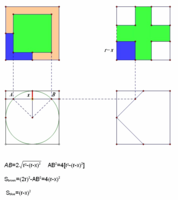
To derive the volume of a bicylinder (white), one can enclose it within a cube (red). When a plane, parallel to the axes of the cylinders, intersects the bicylinder, it forms a square. This plane’s intersection with the cube results in a larger square. The area difference between these two squares corresponds to four smaller squares (blue). As the plane traverses through the solids, these blue squares form square pyramids with isosceles faces at the cube’s corners. The apexes of these pyramids are located at the midpoints of the cube’s four edges. Moving the plane through the entire bicylinder results in a total of eight pyramids.

• 
  Zu Chongzhi's method (similar to Cavalieri's principle) for calculating a sphere's volume includes calculating the volume of a bicylinder.
• 
  Relationship of the area of a bicylinder section with a cube section

The volume of the cube (red) minus the volume of the eight pyramids (blue) is the volume of the bicylinder (white). The volume of the 8 pyramids is: $$8\times {\frac {1}{3}}r^{2}\times r={\frac {8}{3}}r^{3},$$ and then we can calculate that the bicylinder volume is $$(2r)^{3}-{\frac {8}{3}}r^{3}={\frac {16}{3}}r^{3}.$$

Tricylinder

Generating the surface of a tricylinder: At first two cylinders (red, blue) are cut. The so generated bicylinder is cut by the third (green) cylinder.

The intersection of three cylinders with perpendicularly intersecting axes generates a surface of a solid with vertices where 3 edges meet and vertices where 4 edges meet. The set of vertices can be considered as the edges of a rhombic dodecahedron. The key for the determination of volume and surface area is the observation that the tricylinder can be resampled by the cube with the vertices where 3 edges meet (s. diagram) and 6 curved pyramids (the triangles are parts of cylinder surfaces). Similar considerations can determine the volume and the surface area of the curved triangles as it is done for the bicylinder above.

The volume of a tricylinder is $$V=8(2-{\sqrt {2}})r^{3}$$ and the surface area is $$A=24(2-{\sqrt {2}})r^{2}.$$

More cylinders

With four cylinders, with axes connecting the vertices of a tetrahedron to the corresponding points on the other side of the solid, the volume is

$$V_{4}=12\left(2{\sqrt {2}}-{\sqrt {6}}\right)r^{3}\,$$

With six cylinders, with axes parallel to the diagonals of the faces of a cube, the volume is:

$$V_{6}={\frac {16}{3}}\left(3+2{\sqrt {3}}-4{\sqrt {2}}\right)r^{3}\,$$

See also

• Ungula

External links

• A 3D model of Steinmetz solid in Google 3D Warehouse