Bounded variation

In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded (finite): the graph of a function having this property is well behaved in a precise sense. For a continuous function of a single variable, being of bounded variation means that the distance along the direction of y-axis (i.e. the distance calculated neglecting the contribution of motion along x-axis) traveled by an ideal point moving along the graph of the given function (which, under given hypothesis, is also a continuous path) has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function (which is an hypersurface in this case), but can be every intersection of the graph itself with a plane parallel to a fixed x-axis and to the y-axis.

Functions of bounded variation are precisely those with respect to which one may find Riemann-Stieltjes integrals of all continuous functions.

Another characterization states that the functions of bounded variation on a closed interval are exactly those $f$ which can be written as a difference $g-h$, where both $g$ and $h$ are bounded monotone.

In the case of several variables, a function $f$ defined on an open subset $\Omega$ of $\scriptstyle \mathbb {R} ^{n}$ is said to have bounded variation if its distributional derivative is a finite vector Radon measure.

One of the most important aspects of functions of bounded variation is that they form an algebra of discontinuous functions whose first derivative exists almost everywhere: due to this fact, they can and frequently are used to define generalized solutions of nonlinear problems involving functionals, ordinary and partial differential equations in mathematics, physics and engineering. Considering the problem of multiplication of distributions or more generally the problem of defining general nonlinear operations on generalized functions, function of bounded variation are the smallest algebra which has to be embedded in every space of generalized functions preserving the result of multiplication.

History

According to Boris Golubov, BV functions of a single variable were first introduced by Camille Jordan, in the paper (Jordan 1881) dealing with the convergence of Fourier series. The first step in the generalization of this concept to functions of several variables was due to Leonida Tonelli, who introduced a class of continuous BV functions in 1926 (Cesari 1986, pp. 47–48), to extend his direct method for finding solutions to problems in the calculus of variations in more than one variable. Ten years after, in 1936, Lamberto Cesari changed the continuity requirement in Tonelli's definition to a less restrictive integrability requirement, obtaining for the first time the class of functions of bounded variation of several variables in its full generality: as Jordan did before him, he applied the concept to resolve of a problem concerning the convergence of Fourier series, but for functions of two variables. After him, several authors applied BV functions to study Fourier series in several variables, geometric measure theory, calculus of variations, and mathematical physics. Renato Caccioppoli and Ennio de Giorgi used them to define measure of non smooth boundaries of sets (see voice "Caccioppoli set" for further informations). Olga Arsenievna Oleinik introduced his view of generalized solutions for nonlinear partial differential equations as functions from the space $BV$ in the paper (Oleinik 1957): few years after, Edward D. Conway and Joel A. Smoller applied them to the study of a single nonlinear hyperbolic partial differential equation of first order in the paper (Conway & Smoller 1966), proving that the solution of the Cauchy problem for such equations is a function of bounded variation, provided the initial value belongs to the same class. Aizik Isaakovich Vol'pert developed extensively a calculus for BV functions: in the paper (Vol'pert 1967) he proved the chain rule for BV functions and in the book (Hudjaev & Vol'pert 1986) he studied extensively the properties of BV functions and their application. His chain rule formula was later extended by Luigi Ambrosio and Gianni Dal Maso in the paper (Ambrosio & Dal Maso 1990).

Formal definition

BV functions of one variable

Definition 1. The total variation of a real-valued function $f$, defined on an interval $\scriptstyle [a,b]\subset \mathbb {R}$ is the quantity

$V_{b}^{a}(f)=\sup _{P\in {\mathcal {P}}}\sum _{i=0}^{n_{P}-1}|f(x_{i+1})-f(x_{i})|.\,$

where the supremum is taken over the set $\scriptstyle {\mathcal {P}}=\left\{P=\{x_{0},\dots ,x_{n_{p}}\}|P{\text{ is a partition of }}[a,b]\right\}$ of all partitions of the interval considered.

If $f$ is differentiable and its derivative is integrable, its total variation is the vertical component of the arc-length of its graph, that is to say,

$V_{b}^{a}(f)=\int _{a}^{b}|f'(x)|\,dx.$

Definition 2. A real-valued function $f$ on the real line is said to be of bounded variation (BV function) on a chosen interval $[a,b]$ if its total variation is finite, i.e.

$f\in BV([a,b])\iff V_{b}^{a}(f)<+\infty$

It can be proved that a real function $f$ is of bounded variation in an interval if and only if it can be written as the difference $f=f_{1}-f_{2}$ of two non decreasing functions. (This is known as the Jordan decomposition.)

Through the Stieltjes integral, any function of bounded variation on a closed interval $[a,b]$ defines a bounded linear functional on $C([a,b])$. In this special case (Kolmogorov & Fomin 1969, pp. 374–376), the Riesz representation theorem states that every bounded linear functional arises uniquely in this way. The normalised positive functionals or probability measures correspond to positive non-decreasing lower semicontinuous functions. This point of view has been important in spectral theory (Riesz & Sz.-Nagy 1990), in particular in its application to ordinary differential equations.

BV functions of several variables

Functions of bounded variation, BV functions, are functions whose distributional derivative is a finite Radon measure. More precisely:

Definition 1 Let $\Omega$ be an open subset of $\scriptstyle \mathbb {R} ^{n}$. A locally integrable function $u$ is said of bounded variation (BV function), and write

$u\in BV(\Omega )$

if there exists a finite vector Radon measure $\scriptstyle Du\in {\mathcal {M}}(\Omega ,\mathbb {R} ^{n})$ such that the following equality holds

$\int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x=-\int _{\Omega }\langle {\boldsymbol {\phi }},Du(x)\rangle \qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$

that is, $u$ defines a linear functional on the space $\scriptstyle C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ of continuously differentiable vector functions $\scriptstyle {\boldsymbol {\phi }}$ of compact support contained in $\Omega$: the vector measure $Du$ represents therefore the distributional or weak gradient of $u$.

An equivalent definition is the following.

Definition 2 Given a locally integrable function $u$, the total variation of $u$ in is defined as

$V(u,\Omega ):=\sup \left\{\int _{\Omega }u(x)\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x\colon {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n}),\ \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1\right\}$

where $\scriptstyle \Vert \;\Vert _{L^{\infty }(\Omega )}$ is the essential supremum norm. Sometimes, especially in the theory of Caccioppoli sets, the following notation is used

$\int _{\Omega }\vert Du\vert =V(u,\Omega )$

in order to emphasize that $V(u,\Omega )$ is the total variation of the distributional / weak gradient of $u$. This notation reminds also that if $u$ is of class $C^{1}$ (i.e. a continuous and differentiable function having continuous derivatives) then its variation is exactly the integral of the absolute value of its gradient.

The space of functions of bounded variation (BV functions) can then be defined as

$BV(\Omega )=\{u\in L^{1}(\Omega )\colon V(u,\Omega )<+\infty \}$

The two definitions are equivalent since if $\scriptstyle V(u,\Omega )<+\infty$ then

$\left|\int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x\right|\leq V(u,\Omega )\Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$

therefore $\scriptstyle \int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)$ defines a continuous linear functional on the space $\scriptstyle C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$. Since $\scriptstyle C_{c}^{1}(\Omega ,\mathbb {R} ^{n})\subset C^{0}(\Omega ,\mathbb {R} ^{n})$ as a linear subspace, this continuous linear functional can be extended continuously and linearily to the whole $\scriptstyle C^{0}(\Omega ,\mathbb {R} ^{n})$ by the Hahn–Banach theorem i.e. it defines a Radon measure.

Basic properties

Only the properties common to functions of one variable and to functions of several variables will be considered in the following, and proofs will be carried on only for functions of several variables since the proof for the case of one variable is a straightforward adaptation of the several variables case. References (Giusti 1984, pp. 7–9), (Hudjaev & Vol'pert 1986) and (Màlek et al. 1996) are extensively used.

BV functions have only jump-type singularities

In the case of one variable, the assertion is clear: for each point $x_{0}$ in the interval $\scriptstyle ]a,b[\subset \mathbb {R}$ of definition of the function $u$, either one of the following two assertions is true

$\lim _{x\rightarrow x_{0^{-}}}\!\!\!u(x)=\!\!\!\lim _{x\rightarrow x_{0^{+}}}\!\!\!u(x)$

$\lim _{x\rightarrow x_{0^{-}}}\!\!\!u(x)\neq \!\!\!\lim _{x\rightarrow x_{0^{+}}}\!\!\!u(x)$

while both limits exists and are finite. In the case of functions of several variables, there are some premises to understand: first of all, there is a continuum of directions along which it is possible to approach a given point $x_{0}$ belonging to the domain $\scriptstyle \Omega \in \mathbb {R} ^{n}$. It is necessary to make precise a suitable concept of limit: choosing a unit vector $\scriptstyle {\boldsymbol {\hat {a}}}\in \mathbb {R} ^{n}$ it is possible to divide $\Omega$ in two sets

$\Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}=\Omega \cap \{{\boldsymbol {x}}\in \mathbb {R} ^{n}|\langle {\boldsymbol {x}}-{\boldsymbol {x}}_{0},{\boldsymbol {\hat {a}}}\rangle >0\}\qquad \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}=\Omega \cap \{{\boldsymbol {x}}\in \mathbb {R} ^{n}|\langle {\boldsymbol {x}}-{\boldsymbol {x}}_{0},-{\boldsymbol {\hat {a}}}\rangle >0\}$

Then for each point $x_{0}$ belonging to the domain $\scriptstyle \Omega \in \mathbb {R} ^{n}$ of the BV function $u$, only one of the following two assertions is true

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})=\!\!\!\!\!\!\!\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})$

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})\neq \!\!\!\!\!\!\!\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})$

or $x_{0}$ belongs to a subset of $\Omega$ having zero $n-1$-dimensional Hausdorff measure. The quantities

$\lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{({\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!u({\boldsymbol {x}})=u_{\boldsymbol {\hat {a}}}({\boldsymbol {x}})\qquad \lim _{\overset {{\boldsymbol {x}}\rightarrow {\boldsymbol {x}}_{0}}{{\boldsymbol {x}}\in \Omega _{(-{\boldsymbol {\hat {a}}},{\boldsymbol {x}}_{0})}}}\!\!\!\!\!\!\!u({\boldsymbol {x}})=u_{-{\boldsymbol {\hat {a}}}}({\boldsymbol {x}})$

are called approximate limits of the BV function $u$ at the point $x_{0}$.

V(·, Ω) is lower semi-continuous on BV(Ω)

The functional $\scriptstyle V(\cdot ,\Omega ):BV(\Omega )\rightarrow \mathbb {R} ^{+}$ is lower semi-continuous: to see this, choose a Cauchy sequence of BV-functions $\scriptstyle \{u_{n}\}_{n\in \mathbb {N} }$ converging to $\scriptstyle u\in L_{loc}^{1}(\Omega )$. Then, since all the functions of the sequence and their limit function are integrable and by the definition of lower limit

$\liminf _{n\rightarrow \infty }V(u_{n},\Omega )\geq \lim _{n\rightarrow \infty }\int _{\Omega }u_{n}(x)\,\mathrm {div} {\boldsymbol {\phi }}\,dx=\int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}\,dx\qquad \forall {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n}),\quad \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1$

Now considering the supremum on the set of functions $\scriptstyle {\boldsymbol {\phi }}\in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ such that $\scriptstyle \Vert {\boldsymbol {\phi }}\Vert _{L^{\infty }(\Omega )}\leq 1$ then the following inequality holds true

$\liminf _{n\rightarrow \infty }V(u_{n},\Omega )\geq V(u,\Omega )$

which is exactly the definition of lower semicontinuity.

BV(Ω) is a Banach space

By definition $BV(\Omega )$ is a subset of $\scriptstyle L_{loc}^{1}(\Omega )$, while linearity follows from the linearity properties of the defining integral i.e.

${\begin{aligned}\int _{\Omega }[u(x)+v(x)]\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x&=\int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x+\int _{\Omega }v(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x=\\&=-\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Du(x)\rangle -\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Dv(x)\rangle =-\int _{\Omega }\langle {\boldsymbol {\phi }}(x),[Du(x)+Dv(x)]\rangle \end{aligned}}$

for all $\scriptstyle \phi \in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ therefore $\scriptstyle u+v\in BV(\Omega )$for all $\scriptstyle u,v\in BV(\Omega )$, and

$\int _{\Omega }c\cdot u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x=c\!\int _{\Omega }u(x)\,\mathrm {div} {\boldsymbol {\phi }}(x)\mathrm {d} x=-c\!\int _{\Omega }\langle {\boldsymbol {\phi }}(x),Du(x)\rangle$

for all $\scriptstyle c\in \mathbb {R}$, therefore $\scriptstyle cu\in BV(\Omega )$ for all $\scriptstyle u\in BV(\Omega )$, and all $\scriptstyle c\in \mathbb {R}$. The proved vector space properties imply that $BV(\Omega )$ is a vector subspace of $L^{1}(\Omega )$. Consider now the function $\scriptstyle \|\;\|_{BV}:BV(\Omega )\rightarrow \mathbb {R} ^{+}$ defined as

$\|u\|_{BV}:=\|u\|_{L^{1}}+V(u,\Omega )$

where $\scriptstyle \|\;\|_{L^{1}}$ is the usual $L^{1}(\Omega )$ norm: it is easy to prove that this is a norm on $BV(\Omega )$. To see that $BV(\Omega )$ is complete respect to it, i.e. it is a Banach space, consider a Cauchy sequence $\scriptstyle \{u_{n}\}_{n\in \mathbb {R} }$ in $BV(\Omega )$. By definition it is also a Cauchy sequence in $L^{1}(\Omega )$ and therefore has a limit $u$ in $L^{1}(\Omega )$: since $u_{n}$ is bounded in $BV(\Omega )$ for each $n$, then $\scriptstyle \Vert u\Vert _{BV}<+\infty$ by lower semicontinuity of the variation $\scriptstyle V(\cdot ,\Omega )$, therefore $u$ is a BV function. Finally, again by lower semicontinuity, choosing an arbitrary small positive number $\scriptstyle \varepsilon$

$\Vert u_{j}-u_{k}\Vert _{BV}<\varepsilon \quad \forall j,k\geq N\in \mathbb {N} \quad \Rightarrow \quad V(u_{k}-u,\Omega )\leq \liminf _{j\rightarrow +\infty }V(u_{k}-u_{j},\Omega )\leq \varepsilon$

Chain rule for BV functions

Chain rules for nonsmooth functions are very important in mathematics and mathematical physics since there are several important physical models whose behavior is described by functions or functionals with a very limited degree of smoothness.The following version is proved in the paper (Vol'pert 1967, p. 248): all partial derivatives must be intended in a generalized sense. i.e. as generalized derivatives

Theorem. Let $\scriptstyle f:\mathbb {R} ^{p}\rightarrow \mathbb {R}$ be a function of class $C^{1}$ (i.e. a continuous and differentiable function having continuous derivatives) and let $\scriptstyle {\boldsymbol {u}}({\boldsymbol {x}})=(u_{1}({\boldsymbol {x}}),\ldots ,u_{p}({\boldsymbol {x}}))$ be a function in $BV(\Omega )$ with $\Omega$ being an open subset of $\scriptstyle \mathbb {R} ^{n}$. Then $\scriptstyle f\circ {\boldsymbol {u}}({\boldsymbol {x}})=f({\boldsymbol {u}}({\boldsymbol {x}}))\in BV(\Omega )$ and

${\frac {\partial f({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial x_{i}}}=\sum _{k=1}^{p}{\frac {\partial {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial u_{k}}}{\frac {\partial {u_{k}({\boldsymbol {x}})}}{\partial x_{i}}}\qquad \forall i=1,\ldots ,n$

where $\scriptstyle {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))$ is the mean value of the function at the point $\scriptstyle x\in \Omega$, defined as

${\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))=\int _{0}^{1}f\left({\boldsymbol {u}}_{\boldsymbol {\hat {a}}}({\boldsymbol {x}})t+{\boldsymbol {u}}_{-{\boldsymbol {\hat {a}}}}({\boldsymbol {x}})(1-t)\right)dt$

A more general chain rule formula for Lipschitz continuous functions $\scriptstyle f:\mathbb {R} ^{p}\rightarrow \mathbb {R} ^{s}$ has been found by Luigi Ambrosio and Gianni Dal Maso and published in the paper (Ambrosio & Dal Maso 1990). However, even this formula has very important direct consequences: choosing $\scriptstyle f(u)=v({\boldsymbol {x}})u({\boldsymbol {x}})$ where $\scriptstyle v({\boldsymbol {x}})$ is a BV function the preceding formula becomes the Leibnitz rule for $BV$ functions

${\frac {\partial v({\boldsymbol {x}})u({\boldsymbol {x}})}{\partial x_{i}}}={{\bar {u}}({\boldsymbol {x}})}{\frac {\partial v({\boldsymbol {x}})}{\partial x_{i}}}+{{\bar {v}}({\boldsymbol {x}})}{\frac {\partial u({\boldsymbol {x}})}{\partial x_{i}}}$

This implies that the product of two functions of bounded variation is again a function of bounded variation, therefore $BV(\Omega )$ is an algebra.

BV(Ω) is a Banach algebra

This property follows directly from the fact that $BV(\Omega )$ is a Banach space and also an associative algebra: this implies that if $\{v_{n}\}$ and $\{u_{n}\}$ are Cauchy sequences of $BV$ functions converging respectively to functions $v$ and $u$ in $BV(\Omega )$, then

${\begin{matrix}vu_{n}{\xrightarrow[{n\to \infty }]{}}vu\\v_{n}u{\xrightarrow[{n\to \infty }]{}}vu\end{matrix}}\quad \Longleftrightarrow \quad vu\in BV(\Omega )$

therefore the ordinary product of functions is continuous in $BV(\Omega )$ respect to each argument, making this function space a Banach algebra.

Generalizations and extensions

Weighted BV functions

It is possible to generalize the above notion of total variation so that different variations are weighted differently. More precisely, let $\scriptstyle \varphi :[0,+\infty )\longrightarrow [0,+\infty )$ be any increasing function such that $\scriptstyle \varphi (0)=\varphi (0+)=\lim _{x\rightarrow 0_{+}}\varphi (x)=0$ (the weight function) and let $\scriptstyle f:[0,T]\longrightarrow X$ be a function from the interval $\scriptstyle [0,T]\subset \mathbb {R}$ taking values in a normed vector space $X$. Then the $\scriptstyle {\boldsymbol {\varphi }}$-variation of $f$ over $[0,T]$ is defined as

$\mathop {\varphi {\mbox{-Var}}} _{[0,T]}(f):=\sup \sum _{j=0}^{k}\varphi \left(|f(t_{j+1})-f(t_{j})|_{X}\right),$

where, as usual, the supremum is taken over all finite partitions of the interval $[0,T]$, i.e. all the finite sets of real numbers $t_{i}$ such that

$0=t_{0}<t_{1}<\ldots <t_{k}=T.$

The original notion of variation considered above is the special case of $\scriptstyle \varphi$-variation for which the weight function is the identity function: therefore an integrable function $f$ is said to be a weighted BV function (of weight $\scriptstyle \varphi$) if and only if its $\scriptstyle \varphi$-variation is finite.

$f\in BV_{\varphi }([0,T];X)\iff \mathop {\varphi {\mbox{-Var}}} _{[0,T]}(f)<+\infty$

The space $\scriptstyle BV_{\varphi }([0,T];X)$ is a topological vector space with respect to the norm

$\|f\|_{BV_{\varphi }}:=\|f\|_{\infty }+\mathop {\varphi {\mbox{-Var}}} _{[0,T]}(f),$

where $\scriptstyle \|f\|_{\infty }$ denotes the usual supremum norm of $f$. Weighted BV functions were introduced and studied in full generality by Wladislav Orlicz and Julian Musielak in the paper (Musielak & Orlicz 1959): Laurence Chisholm Young studied earlier the case $\scriptstyle \varphi (x)=x^{p}$ where $p$ is a positive integer.

SBV functions

SBV functions i.e. Special functions of Bounded Variation where introduced by Luigi Ambrosio and Ennio de Giorgi in the paper (Ambrosio & De Giorgi 1988), dealing with free discontinuity variational problems: given an open subset $\Omega$ of $\scriptstyle \mathbb {R} ^{n}$, the space $SBV(\Omega )$ is a proper subspace of $BV(\Omega )$, since the weak gradient of each function belonging to it const exatcly of the sum of a $n$-dimensional support and a $n-1$-dimensional support measure and no lower-dimensional terms, as seen in the following definition.

Definition. Given a locally integrable function $u$, then $\scriptstyle u\in {S\!BV}(\Omega )$ if and only if

1. There exist two Borel functions $f$ and $g$ of domain $\Omega$ and codomain $\scriptstyle \mathbb {R} ^{n}$ such that

$\int _{\Omega }\vert f\vert dH^{n}+\int _{\Omega }\vert g\vert dH^{n-1}<+\infty .$

2. For all of continuously differentiable vector functions $\scriptstyle \phi$ of compact support contained in $\Omega$, i.e. for all $\scriptstyle \phi \in C_{c}^{1}(\Omega ,\mathbb {R} ^{n})$ the following formula is true:

$\int _{\Omega }u{\mbox{div}}\phi dH^{n}=\int _{\Omega }\langle \phi ,f\rangle dH^{n}+\int _{\Omega }\langle \phi ,g\rangle dH^{n-1}.$

where $H^{\alpha }$ is the $\alpha$-dimensional Hausdorff measure.

Details on the properties of SBV functions can be found in works cited in the bibliography section: particularly the paper (De Giorgi 1992) contains a useful bibliography.

bv sequences

As particular examples of Banach spaces, Dunford & Schwartz (1958, Chapter IV) consider spaces of sequences of bounded variation, in addition to the spaces of functions of bounded variation. The total variation of a sequence x=(x_i) of real or complex numbers is defined by

$TV(x)=\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

The space of all sequences of finite total variation is denoted by bv. The norm on bv is given by

$\|x\|_{bv}=|x_{1}|+TV(x)=|x_{1}|+\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

With this norm, the space bv is a Banach space.

The total variation itself defines a norm on a certain subspace of bv, denoted by bv₀, consisting of sequences x = (x_i) for which

$\lim _{n\to \infty }x_{n}=0.$

The norm on bv₀ is denoted

$\|x\|_{bv_{0}}=TV(x)=\sum _{i=1}^{\infty }|x_{i+1}-x_{i}|.$

With respect to this norm bv₀ becomes a Banach space as well.

Examples

The function f(x)=sin(1/x) is not of bounded variation.

The function

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

is not of bounded variation on the interval $[0,2/\pi ]$

The function f(x)=x sin(1/x) is not of bounded variation.

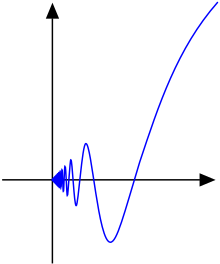
While it is harder to see, the function

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\x\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

is not of bounded variation on the interval $[0,2/\pi ]$ either.

The function f(x)=x² sin(1/x) is of bounded variation.

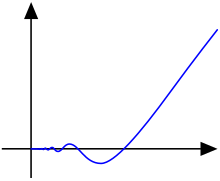
At the same time, the function

$f(x)={\begin{cases}0,&{\mbox{if }}x=0\\x^{2}\sin(1/x),&{\mbox{if }}x\neq 0\end{cases}}$

is of bounded variation on the interval $[0,2/\pi ]$. However, all three functions are of bounded variation on each interval $[a,b]$ with $a>0$.

The Sobolev space $W^{1,1}(\Omega )$ is a proper subset of $BV(\Omega )$. In fact, for each $u$ in $W^{1,1}(\Omega )$ it is possible to choose a measure $\scriptstyle \mu :=\nabla u{\mathcal {L}}$ (where $\scriptstyle {\mathcal {L}}$ is the Lebesgue measure on $\Omega$) such that the equality

$\int u\mathrm {div} \phi =-\int \phi \,d\mu =-\int \phi \nabla u\qquad \forall \phi \in C_{c}^{1}$

holds, since it is nothing more than the definition of weak derivative, and hence holds true. One can easily find an example of a BV function which is not $W^{1,1}$: in dimension one, any step function with a non-trivial jump will do.

Applications

Mathematics

Functions of bounded variation have been studied in connection with the set of discontinuities of functions and differentiability of real functions, and the following results are well-known. If $f$ is a real function of bounded variation on an interval $[a,b]$ then

• $f$ is continuous except at most on a countable set;
• $f$ has one-sided limits everywhere (limits from the left everywhere in $(a,b]$, and from the right everywhere in $[a,b[$ );
• the derivative $f'(x)$ exists almost everywhere (i.e. except for a set of measure zero).

For real functions of several real variables

• the characteristic function of a Caccioppoli set is a BV functions: BV functions lie at the basis of the modern theory of perimeters.
• Minimal surfaces turn out very often to be graphs of BV functions: in this context, see reference (Giusti 1984).

Physics and engineering

The ability of BV functions to deal with discontinuities has made their use widespread in the applied sciences: solutions of problems in mechanics, physics, chemical kinetics are very often representable by functions of bounded variation. The book (Hudjaev & Vol'pert 1986) details a very ample set of mathematical physics applications of BV functions. Also there is some modern application which deserves a brief description.

• The Mumford-Shah functional: the segmentation problem for a two-dimensional image, i.e. the problem of faithful reproduction of contours and grey scales is equivalent to the minimization of such functional.

See also

• Renato Caccioppoli
• Caccioppoli set
• Lamberto Cesari
• Ennio de Giorgi
• Helly's selection theorem
• Locally integrable function
• L^p(Ω) space
• Lebesgue-Stieltjes integral
• Radon measure
• Reduced derivative
• Riemann-Stieltjes integral
• Total variation

References

• Cesari, Lamberto (6-9 June 1985), "L'opera di Leonida Tonelli e la sua influenza nel pensiero scientifico del secolo (the work of Leonida Tonelli and his influence on scientific thinking in this century)", in Montalenti, G.; Amerio, L. et als. (eds.), Convegno celebrativo del centenario della nascita di Mauro Picone e Leonida Tonelli (International congress in occasion of the celebration of the centenary of birth of Mauro Picone and Leonida Tonelli), Atti dei Convegni Lincei, vol. 77, Roma: Accademia Nazionale dei Lincei, pp. 41–73 {{citation}}: Check date values in: |year= / |date= mismatch (help); External link in |title= (help). Some recollections from one of the founders of the theory of BV functions of several variables (in Italian).
• Dunford, Nelson; Jacob T., Schwartz (1958), Linear operators. Part I: General Theory, Pure and Applied Mathematics, vol. VII, New York-London-Sydney: Wiley-Interscience, ISBN 0-471-60848-3. Includes a discussion of the functional-analytic properties of spaces of functions of bounded variation.
• Giusti, Enrico (1984), Minimal surfaces and functions of bounded variations, Monographs in Mathematics, vol. 80, Basel-Boston-Stuttgart: Birkhäuser Verlag, ISBN 0-8176-3153-4 ISBN 3-7643-3153-4 {{citation}}: Check |isbn= value: invalid character (help); External link in |publisher= (help), particularly part I, chapter 1 "Functions of bounded variation and Caccioppoli sets". A good reference on the theory of Caccioppoli sets and their application to the Minimal surface problem.
• Hudjaev, Sergei Ivanovich; Vol'pert, Aizik Isaakovich (1985), Analysis in classes of discontinuous functions and equations of mathematical physics, Mechanics: analysis, vol. 8, Dordrecht-Boston-Lancaster: Martinus Nijhoff Publishers, ISBN 90-247-3109-7. The whole book is devoted to the theory of BV functions and their applications to problems in mathematical physics involving discontinuous functions and geometric objects with non-smooth boundaries.
• Kannan, Rangachary; King Krueger, Carole (1996), Advanced analysis on the real line, Universitext, Berlin-Heidelberg-New York: Springer Verlag, ISBN 0-387-94642-X. Maybe the most complete book reference for the theory of BV functions in one variable: classical results and advanced results are collected in chapter 6 "Bounded variation" along with several exercises. The first author was a collaborator of Lamberto Cesari.
• Kolmogorov, Andrej N.; Fomin, Sergej V. (1969), Introductory Real Analysis, New York: Dover Publications, ISBN 0486612260
• Màlek, Josef; Nečas, Jindřich; Rokyta, Mirko; Růžička, Michael (1996), Weak and measure-valued solutions to evolutionary PDEs, Applied Mathematics and Mathematical Computation, vol. 13, London-Weinheim-New York-Tokyo-Melbourne-Madras: Chapman & Hall/CRC Press, ISBN 0-412-57750-X. One of the most complete monographs on the theory of Young measures, strongly oriented to applications in continuum mechanics of fluids.
• Maz'ya, Vladimir G. (1985), Sobolev Spaces, Berlin-Heidelberg-New York: Springer-Verlag, ISBN 3-540-13589-8, ISBN 0-387-13589-8 {{citation}}: Check |isbn= value: invalid character (help); particularly chapter 6, "On functions in the space $BV(\Omega )$". One of the best monographs on the theory of Sobolev spaces.
• Moreau, Jean Jacques (1988), "Bounded variation in time", in Moreau, J.J.; Panagiotopoulos, P.D.; Strang, G. (eds.), Topics in nonsmooth mechanics., Basel-Boston-Stuttgart: Birkhäuser Verlag, pp. 1–74, ISBN 3-7643-1907-0 {{citation}}: External link in |publisher= (help)
• Musielak, Julian; Orlicz, Wladislaw (1959), "On generalized variations (I)" (PDF), Studia Mathematica, 18, Warszawa-Wrocław: 13–41 {{citation}}: External link in |journal= (help). The first paper where weighted BV functions are studied in full generality.
• Riesz, Frigyes; Szőkefalvi-Nagy, Béla (1990), Functional Analysis, New York: Dover Publications, ISBN ISBN 0-486-66289-6 {{citation}}: Check |isbn= value: invalid character (help)
• Vol'pert, Aizik Isaakovich (1967), "Spaces BV and quasi-linear equations" (PDF), Mathematics USSR-Sbornik, 2 (2): 225–267, retrieved January 23, 2007 {{citation}}: External link in |journal= (help). A seminal paper where Caccioppoli sets and BV functions are deeply studied and applied to the theory of partial differential equations.

Bibliography

• Alberti, Giovanni; Mantegazza, Carlo (1997), "A note on the theory of SBV functions", Bollettino Unione Matematica Italiana, Sezione B, 11 (2): 375–382, Zbl 0877.49001 {{citation}}: External link in |journal= (help). A paper containing a demonstration of the compactness of the space of SBV functions.
• Ambrosio, Luigi; Dal Maso, Giovanni (1990), "A General Chain Rule for Distributional Derivatives", Proceedings of the American Mathematical Society, 108 (3): 691–702, doi:10.2307/2047789, Zbl 0685.49027 {{citation}}: External link in |journal= (help). A paper containing a very general chain rule formula for composition of BV functions.
• Ambrosio, Luigi; De Giorgi, Ennio (1988), "Un nuovo tipo di funzionale del calcolo delle variazioni (A new kind of in the calculus of variations)", Atti della Accademia Nazionale dei Lincei, Rendiconti della Classe di Scienze Fisiche, Matematiche e Naturali, 8, 82 (2): 199–210, Zbl 0715.49014 (in Italian, with English summary. The first paper about SBV functions and related variational problems.
• Conway, Edward D.; Smoller, Joel A. (1966), "Global solutions of the Cauchy problem for quasi-linear first-order equations in several space variables", Communications on Pure and Applied Mathematics, 19 (1): 95–105, MR {{citation}}: External link in |journal= (help). An important paper where properties of BV functions were applied to obtain a global in time existence theorem for single hyperbolic equations of first order in any number of variables.
• De Giorgi, Ennio (1992), "Problemi variazionali con discontinuità libere (Free-discontinuity variational problems)", in Amaldi, E.; Amerio, L., et als. (eds.), Convegno internazionale in memoria di Vito Volterra (International congress in memory of Vito Volterra), 8-11 October 1990, Atti dei Convegni Lincei, vol. 92, Roma: Accademia Nazionale dei Lincei, pp. 133–150 {{citation}}: External link in |title= (help)CS1 maint: multiple names: editors list (link). A survey paper on free-discontinuity variational problems including several details on the theory of SBV functions, their applications and a rich bibliography (in Italian), written by Ennio de Giorgi.
• Oleinik, Olga A. (1957), "Discontinuous solutions of non-linear differential equations", 'UMN', 12 (3(75)): 3–73, Zbl 0080.07701 {{citation}}: External link in |journal= (help) (in Russian). An important paper where the author describes generalized solutions of nonlinear partial differential equations as BV functions.
• Oleinik, Olga A. (1959), "Construction of a generalized solution of the Cauchy problem for a quasi-linear equation of first order by the introduction of "vanishing viscosity"", 'UMN', 14 (2(86)): 159–164, Zbl 0096.06603 {{citation}}: External link in |journal= (help) (in Russian). An important paper where the author consturcts a weak solution in BV for a nonlinear equation partial differential equation with the method of vanishing viscosity.
• Tony F. Chan and Jackie (Jianhong) Shen (2005), Image Processing and Analysis - Variational, PDE, Wavelet, and Stochastic Methods, SIAM Publisher, ISBN 089871589X (with in-depth coverage and extensive applications of Bounded Variations in modern image processing, as started by Rudin, Osher, and Fatemi).

External links

Theory

• Boris I. Golubov (and comments of Anatolii Georgievich Vitushkin) "Variation of a function", Springer-Verlag Online Encyclopaedia of Mathematics.
• "BV function". PlanetMath..
• Jordan, Camille (1881). Sur la série de Fourier. Comptes rendus des Académie des sciences de Paris 92:228-230 [January 23, 2007] (at Gallica). This is, according to Boris Golubov, the first paper on functions of bounded variation.
• Rowland, Todd and Weisstein, Eric W. "Bounded Variation". From MathWorld—A Wolfram Web Resource.

Other

• Luigi Ambrosio home page at the Scuola Normale Superiore, Pisa. Academic home page (with preprints and publications) of one of the contributors to the theory and applications of BV functions.
• Research Group in Calculus of Variations and Geometric Measure Theory, Scuola Normale Superiore, Pisa.
• Aizik Isaakovich Vol'pert at Technion. Academic home page of one of the leading contributors to the theory of BV functions.

---

BV function at PlanetMath.