Logarithm: Difference between revisions
Small additions + math cleanup |
Undid previous edit. No need to "clean up". Strive for consistency in notation, in this article math markup is only used when necessary. |
||
| Line 1: | Line 1: | ||
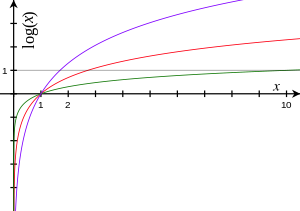
[[Image:Logarithms.svg|thumb|300px|Logarithm functions, graphed for various bases: <span style="color:red">red</span> is to base ''<span style="color:red">e</span>'', <span style="color:green">green</span> is to base <span style="color:green">10</span>, and <span style="color:purple">purple</span> is to base <span style="color:purple">1.7</span>. Each tick on the axes is one unit. Logarithms of all bases pass through the point (1, 0), because any non-zero number raised to the power 0 is 1, and through the points (''b'', 1) for base ''b'', because a number raised to the power 1 is itself. The curves approach the ''y''-axis but do not reach it because of the [[Mathematical singularity|singularity]] at ''x'' = 0 (a vertical [[asymptote]]).]] |
[[Image:Logarithms.svg|thumb|300px|Logarithm functions, graphed for various bases: <span style="color:red">red</span> is to base ''<span style="color:red">e</span>'', <span style="color:green">green</span> is to base <span style="color:green">10</span>, and <span style="color:purple">purple</span> is to base <span style="color:purple">1.7</span>. Each tick on the axes is one unit. Logarithms of all bases pass through the point (1, 0), because any non-zero number raised to the power 0 is 1, and through the points (''b'', 1) for base ''b'', because a number raised to the power 1 is itself. The curves approach the ''y''-axis but do not reach it because of the [[Mathematical singularity|singularity]] at ''x'' = 0 (a vertical [[asymptote]]).]] |
||
In [[mathematics]], the '''logarithm''' of a number to a given ''[[Radix|base]]'' is the [[Power (mathematics)|power]] or [[exponent]] to which the base must be raised in order to produce that number. For example, the logarithm of |
In [[mathematics]], the '''logarithm''' of a number to a given ''[[Radix|base]]'' is the [[Power (mathematics)|power]] or [[exponent]] to which the base must be raised in order to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 3 is the power to which ten must be raised to produce 1000: 10<sup>3</sup> = 1000. The logarithm of ''x'' to the base ''b'' is written log<sub>''b''</sub>(''x'') or log(''x'') when the base ''b'' is implicit. |
||
By the following formulas, logarithms reduce multiplication to addition |
By the following formulas, logarithms reduce multiplication to addition and exponentiation to products: |
||
:log<sub>''b''</sub>(''x'' · ''y'') = log<sub>''b''</sub>(''x'') + log<sub>''b''</sub>(''y''), |
|||
:log<sub>''b''</sub>(''x''<sup>''p''</sup>) = ''p'' log<sub>''b''</sub>(''x''). |
|||
| ⚫ | Three particular values for the base ''b'' are most common. The [[natural logarithm]], the one with base {{nowrap begin}}''b'' = [[e (mathematical constant)|e]]{{nowrap end}}, occurs in [[calculus]] since its [[derivative]] is 1/''x''. The logarithm to base {{nowrap begin}}''b'' = 10{{nowrap end}} is called [[common logarithm]], while the base {{nowrap begin}}''b'' = 2{{nowrap end}} gives rise to the [[binary logarithm]]. |
||
:<math> \log_b(x \cdot y) = \log_b(x)+\log_b(y) \,</math> |
|||
:<math> \log_b(\tfrac{x}{y}) = \log_b(x)-\log_b(y) \,</math> |
|||
:<math> \log_b(x^p) = p\log_b(x) \,</math> |
|||
| ⚫ | Three particular values for the base |
||
The invention of logarithms is due to [[John Napier|John Napier's]] in the early 17th century. Since then, via [[logarithm table]]s, logarithms were a crucial key to simplifying scientific calculations. Today's applications of logarithms are numerous. [[Logarithmic scale]] reduces wide-ranging quantities to smaller scopes; this is applied in the [[Richter scale]], for example. In addition to being a standard function used in various scientific formulas, logarithms appear in determining the [[complexity theory|complexity of algorithms]] and of [[fractal]]s. They also form the mathematical backbone of [[Interval (music)|musical intervals]] and some models in [[psychophysics]], and have been used in [[forensic accounting]]. Logarithms are also closely related to questions revolving around [[prime-counting function|counting prime numbers]]. |
The invention of logarithms is due to [[John Napier|John Napier's]] in the early 17th century. Since then, via [[logarithm table]]s, logarithms were a crucial key to simplifying scientific calculations. Today's applications of logarithms are numerous. [[Logarithmic scale]] reduces wide-ranging quantities to smaller scopes; this is applied in the [[Richter scale]], for example. In addition to being a standard function used in various scientific formulas, logarithms appear in determining the [[complexity theory|complexity of algorithms]] and of [[fractal]]s. They also form the mathematical backbone of [[Interval (music)|musical intervals]] and some models in [[psychophysics]], and have been used in [[forensic accounting]]. Logarithms are also closely related to questions revolving around [[prime-counting function|counting prime numbers]]. |
||
Revision as of 20:28, 6 October 2010
In mathematics, the logarithm of a number to a given base is the power or exponent to which the base must be raised in order to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 3 is the power to which ten must be raised to produce 1000: 103 = 1000. The logarithm of x to the base b is written logb(x) or log(x) when the base b is implicit.
By the following formulas, logarithms reduce multiplication to addition and exponentiation to products:
- logb(x · y) = logb(x) + logb(y),
- logb(xp) = p logb(x).
Three particular values for the base b are most common. The natural logarithm, the one with base b = e, occurs in calculus since its derivative is 1/x. The logarithm to base b = 10 is called common logarithm, while the base b = 2 gives rise to the binary logarithm.
The invention of logarithms is due to John Napier's in the early 17th century. Since then, via logarithm tables, logarithms were a crucial key to simplifying scientific calculations. Today's applications of logarithms are numerous. Logarithmic scale reduces wide-ranging quantities to smaller scopes; this is applied in the Richter scale, for example. In addition to being a standard function used in various scientific formulas, logarithms appear in determining the complexity of algorithms and of fractals. They also form the mathematical backbone of musical intervals and some models in psychophysics, and have been used in forensic accounting. Logarithms are also closely related to questions revolving around counting prime numbers.
Logarithms have been generalized in various ways. The complex logarithm applies to complex numbers instead of real numbers. The discrete logarithm is an important primer in public-key cryptography.
Logarithm of positive real numbers
The logarithm of a number y with respect to a number b is the power to which b has to be raised in order to give y. The number b is called base. In symbols, the logarithm is the number x solving the following equation:
- bx = y.[1]
The logarithm x is denoted logb(y). (Some European countries write blog(y) instead.[2]) For b = 2, for example, this means
- log2(8) = 3,
since 23 = 2 · 2 · 2 = 8. Another example is
since
The first equality is because a−1 is the reciprocal of a, 1 / a, for any number a unequal to zero. A third example, log10(150) is approximately 2.176. Indeed, 102 = 100 and 103 = 1000. As 150 lies between 100 and 1000, its logarithm lies between 2 and 3. Ways of calculating the logarithm are explained further down.
The logarithm logb(y) is defined for any positive number y and any positive base b which is unequal to 1. These restrictions are explained below.
Logarithmic identities
There are three important formulas, sometimes called logarithmic identities, relating various logarithms to one another. The first is about the logarithm of a product, the second about logarithms of powers and the third involves logarithms with respect to different bases.
Logarithm of a product
The logarithm of a product is the sum of the two logarithms. That is, for any two positive real numbers x and y, and a given positive base b, the following identity holds:
- logb(x · y) = logb(x) + logb(y).
For example,
- log3(9 · 27) = log3(243) = 5,
since 35 = 243. On the other hand, the sum of log3(9) = 2 and log3(27) = 3 also equals 5. Another helpful special case of this rule is the following: for any positive number x, logb(b · x) = logb(b) + logb(x) = 1 + logb(x). In other words, multiplying the number x by the base b amounts to adding one to its logarithm. In general, that identity is proven using the following relation of powers and multiplication:
- bs · bt = bs + t.
Substituting the particular values s = logb(x) and t = logb(y) gives
- blogb(x) · blogb(y) = blogb(x) + logb(y).
The left hand side agrees with x · y. Indeed, by the above definition, the logarithm of x is the number to which the base b has to be raised in order to yield x. In other words, the following identity holds:
- x = blogb(x)
and a similar equality holds with y in place of x. Taking the base-b-logarithm of both sides yields
- logb(x · y) = logb(blogb(x) + logb(y)) = logb(x) + logb(y).
Logarithms also convert divisions to subtractions:
for example
Logarithm of a power
The logarithm of the p-th power of a number x is p times the logarithm of that number. In symbols:
- logb(xp) = p · logb(x).
Also, logarithms relate roots to division:
As an example, the logarithm to base b = 2 of 64 is 6, since 26 = 64. But 64 is also 43 and indeed 3 · log2(4) = 3 · 2 equals 6. This formula can be derived by raising the afore-mentioned identity
- x = blogb(x)
to the p-th power (exponentiation). This gives
- xp = (blogb(x))p = bp · logb(x).
For the second equality, the identity (de)f = de · f was used. Thus, the logb of the left hand side, logb(xp), and of the right hand side, p · logb(x), agree. The sought formula is proven.
Change of base
The following formula relates the logarithm of a fixed number x to one base in terms of the one to another base:
This is actually a consequence of the previous rule, as the following proof shows: taking the base-k-logarithm of the above-mentioned identity,
- x = blogb(x),
yields
- logk(x) = logk(blogb(x)).
By the previous rule, the right hand term equals logb(x) · logk(b). Dividing the preceding equation by logk(b) shows the change-of-base formula. The division is possible since logkb ≠ 0. Indeed, this logarithm cannot be zero, since k0 = 1, but b was supposed to be different than 1.
As a practical consequence, logarithms with respect to any base k can be calculated, e.g. using a calculator, if logarithms to the base b are unavailable. From a more theoretical viewpoint, this result implies that the graphs of all logarithm functions (whatever the base b) are similar to each other.
Particular bases
While the definition of logarithm applies to any positive real number b (excluding 1), a few particular choices for b are more commonly used. These are b = 10, b = e (the mathematical constant ≈ 2.71828…), and b = 2. The different standards come about because of the different properties preferred in different fields. For example, it has been argued that common logarithms are easier to deal with than other ones, since in the decimal number system the powers of 10 have a simple representation.[3] Mathematical analysis, on the other hand, prefers the base b = e because of the "natural" properties explained below.
The following table lists common notations for logarithms to these bases and the fields where they are used. Instead of writing logb(x), it is common in many disciplines to omit the base, log(x), when the intended base can be determined from the context. The notations suggested by the International Organization for Standardization (ISO 31-11) are underlined in the table below.[4] Given a number n and its logarithm logb(n), the base b can be determined by the following formula:
This follows from the change-of-base formula above.
| Base b | Name for logb(x) | Notations for logb(x) | Used in |
|---|---|---|---|
| 2 | binary logarithm | lb(x),[5] ld(x), log(x) (in computer science), lg(x)[6] |
computer science, information theory |
| e | natural logarithm | ln(x),[a] log(x) (in mathematics and many programming languages,[7]) |
mathematical analysis, physics, chemistry, statistics, economics and some engineering fields |
| 10 | common logarithm | lg(x),[8] log(x) (in engineering, biology, astronomy), |
various engineering fields, (see decibel and see below), logarithm tables, handheld calculators |
Analytic properties
Logarithm as a function
The expression logb(x) depends on both the base b and on x. As in most situations, in this section b is regarded as fixed. Therefore the logarithm only depends on the variable x, a positive real number. Assigning to x its logarithm logb(x) therefore is a function. It is called logarithm function or logarithmic function or even just logarithm.

The above definition of logarithms was done indirectly by means of the exponential function f(x) = bx: the logarithm (to base b) of y is the solution x to the equation
- f(x) = y.
A rigorous proof that this equation actually has a solution and that this solution is unique requires some elementary calculus, specifically the intermediate value theorem.[citation needed] This theorem says that a continuous function that takes two values m and n also takes any intermediate value, that is, any value that lies between m and n. A function is continuous if it does not "jump", that is, if its graph can be drawn without lifting the pen. This property can be shown to hold for the exponential function f(x). Moreover, it takes arbitrarily big and arbitrarily small positive values, so that any number y can be boxed by y0 and y1 which are values of the function f. Thus, the intermediate value theorem ensures that the equation
- f(x) = y
has a solution. Moreover, as the function f is strictly increasing (for b > 1), or strictly decreasing (for 0 < b < 1), there can only be one solution to this equation.
A compact way of rephrasing the point that the base-b logarithm of y is the solution x to the equation f(x) = bx = y is to say that the logarithm function is the inverse function of the exponential function. Inverse functions are closely related to the original functions: the graphs of the two correspond to each other upon reflecting them at the diagonal line x = y, as shown at the right: a point (t, u = bt) on the graph of the exponential function yields a point (u, t = logbu) on the graph of the logarithm and vice versa. Moreover, analytic properties of the function pass to its inverse function.[9] Thus, as the exponential function f(x) = bx is continuous and differentiable, so is its inverse function, logb(x). Roughly speaking, a differentiable function is one whose graph has no sharp "corners".
Derivative and antiderivative

The derivative of the natural logarithm is given by
This can be derived from the definition as the inverse function of ex, using the chain rule.[10] This implies that the antiderivative of 1/x is ln(x) + C. This fact was used by de Saint-Vincent in 1647 to solve the problem of quadrature of a hyperbolic sector, as shown at the right. The derivative with a generalised functional argument f(x) is
For this reason the quotient at right hand side is called logarithmic derivative of f. The antiderivative of the natural logarithm ln(x) is
Derivatives and antiderivatives of logarithms to other bases can be derived therefrom using the formula for change of bases.
Integral representation of the natural logarithm

The natural logarithm ln(t) = loge(t) satisfies the following identity:
In prose, the natural logarithm of t agrees with the integral of 1/x dx from 1 to t, that is to say, the area between the x-axis and the function 1/x, ranging from x = 1 to x = t. This is depicted at the right. The formula is a consequence of the fundamental theorem of calculus and the above formula for the derivative of ln(x). Some authors actually use the right hand side of this equation as a definition of the natural logarithm and derive the formulas concerning logarithms of products and powers mentioned above from this definition.[11] The product formula ln(tu) = ln(t) + ln(u) is deduced in the following way:
The "=" labelled (1) used a splitting of the integral into two parts, the equality (2) is a change of variable (w = x/t). This can also be understood geometrically. The integral is split into two parts (shown in yellow and blue). The key point is this: rescaling the left hand blue area in vertical direction by the factor t and shrinking it by the same factor in the horizontal direction does not change its size. Moving it appropriately, the area fits the graph of the function 1/x again. Therefore, the left hand area, which is the integral of f(x) from t to tu is the same as the integral from 1 to u:

The power formula ln(tr) = r ln(t) is derived similarly:
The second equality is using a change of variables, w := x1/r, while the third equality follows from integration by substitution.
The sum over the reciprocals of natural numbers, the so-called harmonic series
is also closely tied to the natural logarithm: as n tends to infinity, the difference
converges (i.e., gets arbitrarily close) to a number known as Euler–Mascheroni constant. Little is known about it—not even whether it is a rational number or not.[12]
Calculation
Taylor series
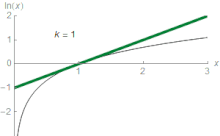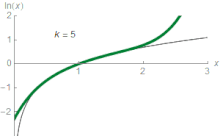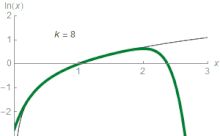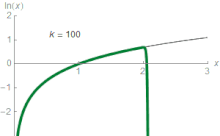
There are several series for calculating natural logarithms.[13] For all complex numbers z satisfying |1 − z| < 1, a simple, though inefficient, series is
Actually, this is the Taylor series expansion of the natural logarithm at z = 1. It is derived from the geometric series (which is the Taylor series of 1/(1 − x)), which converges for |x| < 1:
Taking the indefinite integral of both sides yields
and the above expression is obtained by substituting x by 1 − z (so that 1 − x = z).
More efficient series
Another series is
for complex numbers z with positive real part. This series can be derived from the above Taylor series. The series converges most quickly if z is close to 1. For example, for z = 1.5, the first three terms of this series approximate ln(1.5) with an error of about 3·10−6. (For comparison, the above Taylor series needs 13 terms to achieve that precision.) The quick convergence for z close to 1 can be taken advantage of in the following way: given a low-accuracy approximation y ≈ ln(z) and putting A = z/exp(y), the logarithm of z is
- ln(z) = y + ln(A).
The better the initial approximation y is, the closer A is to 1, so its logarithm can be calculated efficiently. The calculation of A can be done using the exponential series, which converges quickly provided y is not too large. Calculating the logarithm of larger z can be reduced to smaller values of z by writing z = a · 10b, so that ln(z) = ln(a) + b · ln(10).
Computation using significands
In most computers, real numbers are modelled by floating points, which are usually stored as
- x = m · 2n.
In this representation m is called significand and n is the exponent. Therefore
- logb(x) = logb(m) + n logb(2),
so that in order to compute the logarithm of x, it suffices to calculate logb(m) for some m such that 1 ≤ m < 2. Having m in this range means that the value u = (m − 1)/(m + 1) is always in the range 0 ≤ u < 1/3. Some machines use the significand in the range 0.5 ≤ m < 1 and in that case the value for u will be in the range −1/3 < u ≤ 0. In either case, the series is even easier to compute.
The binary (base b = 2) logarithm of a number x can be approximated using the binary logarithm algorithm.
Complex logarithm
The complex logarithm is a generalization of the above definition of logarithms of positive real numbers to complex numbers. Complex numbers are commonly represented as z = x + iy, where x and y are real numbers and i is the imaginary unit. Unlike the case when z is a real number, the equation
- ea = z.
has multiple complex numbers a as solutions, i.e., there are multiple complex numbers a whose exponential equals z. In fact, for any z ≠ 0 there are infinitely many.
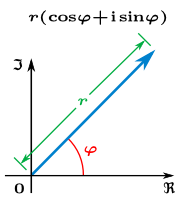
The solutions of the above equation are most readily described using the polar form of z. It encodes a complex number z by its absolute value, that is, the distance r to the origin, and the argument φ, the angle between the line connecting the origin and z and the x-axis. Using the trigonometric functions sine and cosine, r and φ are such that
- z = r · cos(φ) + i · r · sin(φ).[14]
The absolute value r is given by . There are multiple numbers φ such that the preceding equation holds: given one such φ,
- φ' = φ + 2π
also satisfies the above equation. Adding 2π to the argument corresponds to "winding" around the circle counter-clock-wise by an angle of 2π (360 degrees). It is a fact proven in complex analysis that
- z = reiφ.
Consequently,
- a = ln(r) + i φ
is such that the a-th power of e equals z, so that a qualifies being called the complex logarithm of z.

While the argument φ is not uniquely specified, there is exactly one argument φ satisfying −π < φ and φ ≤ π. It is called the principal argument and denoted Arg(z), with a capital A.[15] (The normalization 0 ≤ φ < 2π for the principal argument also appears in the literature.[16]) When φ is chosen to be the principal argument, a is called principal value of the logarithm, denoted Log(z). The principal argument of any positive real number is 0; hence the principal logarithm of such a number is always real and equals the natural logarithm. In contrast to the real case, analogous formula for principal values of logarithm of products and powers for complex numbers do in general not hold.
The graph at the right depicts Log(z). The discontinuity, i.e., jump in the hue at the negative part of the x-axis is due to jump of the principal argument at this locus. This behavior can only be circumvented by dropping the range restriction on φ. Then, however, both the argument of z and, consequently, its logarithm become multi-valued functions. In fact, any logarithm of z can be shown to be of the form
- ln(r) + i (φ + 2nπ),
where φ is the principal argument Arg(z).
Uses and occurrences

Logarithms appear in many places, within and outside mathematics. The logarithmic spiral, for example, appears (approximately) in various guises in nature, such as the shells of nautilus.[17] Logarithms also appear in formulas in various sciences, such as the Tsiolkovsky rocket equation, the Fenske equation, or the Nernst equation.
The logarithm of a positive integer x to a given base shows how many digits are needed to write that integer in that base. For instance, the common logarithm log10(x) is linked to the number n of numerical digits of x: n is the smallest integer strictly bigger than log10(x), i.e., the one satisfying the inequalities:
- n − 1 ≤ log10(x) < n.
Similarly, the number of binary digits (or bits) needed to store a positive integer x is the smallest integer strictly bigger than log2(x).
Logarithmic scale

Various quantities in science are expressed as logarithms of other quantities, a concept known as logarithmic scale. For example, the Richter scale measures the strength of an earthquake by taking the common logarithm of the energy emitted at the earthquake. Thus, an increase in energy by a factor of 10 adds one to the Richter magnitude; a 100-fold energy results in +2 in the magnitude etc.[18] Considering the logarithm instead of the value, here the energy of the quake, reduces the range of possible values to a much smaller range. A second example is the pH in chemistry: it is the negative of the base-10 logarithm of the activity of hydronium ions (H3O+, the form H+ takes in water).[19] The activity of hydronium ions in neutral water is 10−7 mol·L−1 at 25 °C, hence a pH of 7. Vinegar (typically around 5% w/v aqueous solution of acetic acid), on the other hand, has a pH of about 3. The difference of 4 corresponds to a ratio of 104 of the activity, that is, vinegar's hydronium ion activity is about 10−3 mol·L−1. In a similar vein, the decibel (symbol dB) is a unit of measure which is the base-10 logarithm of ratios. For example it is used to quantify the loss of voltage levels in transmitting electrical signals[20] or to describe power levels of sounds in acoustics.[21] In spectrometry and optics, the absorbance unit used to measure optical density is equivalent to −10 dB. The apparent magnitude measures the brightness of stars logarithmically.
Semilog graphs or log-linear graphs use this concept for visualization: one axis, typically the vertical one, is scaled logarithmically. This way, exponential functions of the form f(x) = a · bx appear as a straight line whose slope is proportional to b. In a similar vein, log-log graphs scale both axes logarithmically.[22]
Psychology
In psychophysics, the Weber–Fechner law proposes a logarithmic relationship between stimulus and sensation (though Stevens' power law is typically more accurate). The logarithm appears in situations when the smallest change ΔS of some stimulus S that an observer can still notice is proportional to S, by the above relation of the natural logarithm and the integral over dS / S. (Similar formulas also appear in other sciences, such as the Clausius–Clapeyron relation.) Hick's law proposes a logarithmic relation between the time individuals take for choosing an alternative and the number of choices they have.[23]
Mathematically untrained individuals tend to estimate numerals with a logarithmic spacing, i.e., the position of a presented numeral correlates with the logarithm of the given number so that smaller numbers are given more space than bigger ones. With increasing mathematical training this logarithmic representation becomes more and more linear, as confirmed both in Western school children, comparing second to sixth graders,[24] as well as in comparison between American and indigene cultures.[25]
Complexity and entropy
A function f(x) is said to grow logarithmically, if it is (sometimes approximately) proportional to the logarithm. (Biology, in describing growth of organisms, uses this term for an exponential function, though.[26]) It is irrelevant to which base the logarithm is taken, since choosing a different base amounts to multiplying the result by a constant, as follows from the formula above. For example, any natural number N can be represented in binary form in no more than (log2(N)) + 1 bits. I.e., the amount of hard disk space on a computer grows logarithmically as a function of the size of the number to store. Corresponding calculations carried out using loge will lead to results in nats which may lack this intuitive interpretation. However, the change amounts to a factor of loge2≈0.69—twice as many values can be encoded with one additional bit, which corresponds to an increase of about 0.69 nats. A similar example is the relation of decibel (dB), using a common logarithm (b = 10) vis-à-vis neper, based on a natural logarithm.
Some disciplines disregard the factor resulting from choosing different bases of logarithms. For example, complexity theory, a branch of computer science, describes the asymptotic behavior of algorithms by making statements like "the behavior of the algorithm is logarithmic". For example, sorting N items using the quicksort algorithm typically requires time proportional to the product N · log(N). Using big O notation, the complexity is denoted as
- O(N · log(N)),
which is a lot slower a growth than, say the complexity O(N2) of bubble sort.
Using logarithms, the notion of entropy in information theory is a measure of quantity of information. If a message recipient may expect any one of N possible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified as log2 N bits.[27] In the same vein, the concept of entropy also appears in thermodynamics. Fractal dimension and Hausdorff dimension measure how much space geometric structures occupy.
| Example | point | (straight) line | Koch curve | Sierpinski triangle | plane | Apollonian sphere |

|

| |||||
| Hausdorff dimension | 0 | 1 | log(4)/log(3) ≈ 1.262 | log(3)/log(2) ≈ 1.585 | 2 | ≈ 2.474 |
Pure mathematics

Natural logarithms have a tendency to appear in number theory. For any given number x, the number of prime numbers less than or equal to x is denoted π(x). In its simplest form, the prime number theorem asserts that π(x) is approximately given by
in the sense that the ratio of π(x) and that fraction approaches 1 when x tends to infinity.[28] This can be rephrased by saying that the probability that a randomly chosen number between 1 and x is prime is indirectly proportional to the numbers of decimal digits of x. A far better estimate of π(x) is given by the offset logarithmic integral function Li(x), defined by
The Riemann hypothesis, one of the oldest open mathematical conjectures, can be stated in terms of comparing π(x) and Li(x).[29] The Erdős–Kac theorem describing the number of distinct prime factors also involves the natural logarithm.
By the formula calculating logarithms of products, the logarithm of n factorial, n! = 1 · 2 · ... · n, is given by
- ln(n!) = ln(1) + ln(2) + ... + ln(n).
This can be used to obtain Stirling's formula, an approximation for n! for large n.[30]
In geometry the logarithm is used to calculate the distance on the Poincaré half-plane model of the hyperbolic geometry.[citation needed]
Probability theory and statistics
The law of the iterated logarithm in probability theory describes the magnitude of the fluctuations of a random walk, such as a tossing a coin repeatedly.
In inferential statistics, the logarithm of the data in a dataset can be used for parametric statistical testing if the original data do not meet the assumption of normality.[citation needed] A log-normal distribution is one whose logarithm is normally distributed.[31]
Logarithms appear in Benford's law, an empirical description of the occurrence of digits in certain real-life data sources, such as heights of buildings. The probability that the first decimal digit of the data in question is d (from 1 to 9) equals
- log10(d + 1) − log10(d),
irrespective of the unit of measurement.[32] Thus according to that law, about 30% of the data can be expected to have 1 as first digit, 18% start with 2 etc. Deviations from this pattern can be used to detect fraud in accounting.[33]
Music
Logarithms appear in the encoding of musical tones. In equal temperament, the frequency ratio depends only on the interval between two tones, not on the specific frequency, or pitch of the individual tones. Therefore, logarithms can be used to describe the intervals: the interval between two notes in semitones is the base-21/12 logarithm of the frequency ratio.[34] For finer encoding, as it is needed for non-equal temperaments, intervals are also expressed in cents, hundredths of an equally-tempered semitone. The interval between two notes in cents is the base-21/1200 logarithm of the frequency ratio (or 1200 times the base-2 logarithm). The table below lists some musical intervals together with the frequency ratios and their logarithms.
| Interval (two tones are played at the same time) | 1/72 tone | Semitone | Just major third | Major third | Tritone | Octave |
| Frequency ratio r | 2 | |||||
| , i.e., corresponding number of semitones | 1/6 | 1 | ≈ 3.86 | 4 | 6 | 12 |
| , i.e., corresponding number of cents | 16.67 | 100 | ≈ 386.31 | 400 | 600 | 1200 |
Related operations and generalizations
The cologarithm of a number is the logarithm of the reciprocal of the number: cologb(x) = logb(1/x) = −logb(x). This terminology is found primarily in older books.[35] The antilogarithm function antilogb(y) is the inverse function of the logarithm function logb(x); it can be written in closed form as by.[36] The antilog notation was common before the advent of modern calculators and computers: tables of antilogarithms to the base 10 were useful in carrying out computations by hand.[37] Today's applications of antilogarithms include certain electronic circuit components known as antilog amplifiers.[38]
The double or iterated logarithm, ln(ln(x)), is the inverse function of the double exponential function. The super- or hyper-4-logarithm is the inverse function of tetration. The super-logarithm of x grows even more slowly than the double logarithm for large x. The Lambert W function is the inverse function of ƒ(w) = wew.
From the pure mathematical perspective, the identity log(cd) = log(c) + log(d) expresses an isomorphism between the multiplicative group of the positive real numbers and the group of all the reals under addition. Logarithmic functions are the only continuous isomorphisms from the multiplicative group of positive real numbers to the additive group of real numbers.[39] By means of that isomorphism, the Lebesgue measure dx on R corresponds to the Haar measure dx/x on the positive reals.[40] In complex analysis and algebraic geometry, differential forms of the form (d log(f) =) df/f are known as forms with logarithmic poles.[41] This notion in turn gives rise to concepts such as logarithmic pairs, log terminal singularities or logarithmic geometry.
The polylogarithm is a function defined as
It generalizes the natural logarithm in that Li1(z) = −ln(1 − z). On the other hand, Lis(1) equals the Riemann zeta function ζ(s).
The discrete logarithm is a related notion in the theory of finite groups. It involves solving the equation bn = x, where b and x are elements of the group, and n is an integer specifying a power in the group operation. Zech's logarithm is related to the discrete logarithm in the multiplicative group of non-zero elements of a finite field.[42] For some finite groups, it is believed that the discrete logarithm is very hard to calculate, whereas discrete exponentials are quite easy. This asymmetry has applications in public key cryptography, more specifically in elliptic curve cryptography.[43]
For p-adic numbers, the logarithm can also be defined as the inverse function of the exponential. However, the p-adic exponential and thus the logarithm have smaller domains of definition than in the real or complex case.[44] The logarithm of a matrix is the inverse function of the matrix exponential.[45]
History
Predecessors
The Indian mathematician Virasena worked with the concept of ardhaccheda: the number of times a number could be halved; effectively similar to the integer part of logarithms to base 2. He described various relations[which?] using this operation as well as working with logarithms in base 3 (trakacheda) and base 4 (caturthacheda).[46][47]
Michael Stifel published Arithmetica integra in Nuremberg in 1544; it contains a table of integers and powers of 2 that some have considered to be an early version of a logarithmic table.[48][49]
John Napier

The method of logarithms was publicly propounded in 1614, in a book entitled Mirifici Logarithmorum Canonis Descriptio, by John Napier.[50] (Joost Bürgi independently discovered logarithms; however, he did not publish his discovery until four years after Napier).
By repeated subtractions Napier calculated 107(1 − 10−7)L for L ranging from 1 to 100. The result for L=100 is approximately 0.99999 = 1 − 10−5. Napier then calculated the products of these numbers with 107(1 − 10−5)L for L from 1 to 50 and finally did similarly with 0.9995 ≈ (1 − 10−5)20. These computations, which occupied Napier for 20 years, allowed to give for any number N between 0 and 107, the number L solving the equation
- N = 107(1 − 10−7)L.
Napier first called L "artificial number", but later introduced the word "logarithm" to mean a number that indicates a ratio: λόγος (logos) meaning proportion, and ἀριθμός (arithmos) meaning number. In modern notation, L is approximately equal to 107log1/e(N/107), because (1 − 10−7)107 is approximately 1/e. However, the number e and the modern definition for logarithms were developed about 100 years later, by Euler in 1728.[51][52]
The invention of logarithms was quickly met with acclaim in many countries. The work of Cavalieri (Italy), Wingate (France), Fengzuo (China), and Kepler's Chilias logarithmorum (Germany) helped spread the concept further.[53]
Tables of logarithms and historical applications

Logarithms contributed to the advance of science, and especially of astronomy. Prior to their invention, the more involved method of prosthaphaeresis, which relied on trigonometric identities, was used to approximately calculate products. Until the advent of calculators and computers, logarithms were used constantly in surveying, celestial navigation, and other branches of practical mathematics. Once the invention of the chronometer made possible the accurate measurement of longitude at sea, mariners had everything necessary to reduce their navigational computations to mere additions.[citation needed]
The calculation of products using logarithms stakes on the following formula:
- c · d = blogbc · blogbd = b(logbc + logbd).
The base b is fixed. Many tables use the common logarithm, i.e., b = 10. The logarithms logbc and logbd are looked up in a table of logarithms. Calculating the sum of the logarithms is an easy operation. Finally, raising b to the power of this sum (historically called antilogarithm) is again done by looking up a table. For manual calculations that demand any appreciable precision, this process, requiring three lookups and a sum, is much faster than performing the multiplication. To achieve seven decimal places of accuracy requires a table that fills a single large volume; a table for nine-decimal accuracy occupies a few shelves.[citation needed] The precision of the approximation can be increased by interpolating between table entries.
Calculation of powers are reduced to multiplications and look-ups by
- cd = b(logbc) · d.
Divisions and roots are also covered by these two techniques since
and
- .
The following table lists the major tables of logarithms compiled in history:
| Year | Author | Range | Decimal places | Note |
|---|---|---|---|---|
| 1617 | Henry Briggs | 1–1000 | 8 | |
| 1624 | Henry Briggs Arithmetica Logarithmica | 1–20,000, 90,000–100,000 | 14 | |
| 1628 | Adriaan Vlacq | 20,000–90,000 | 10 | contained only 603 errors[54] |
| 1792–94 | Gaspard de Prony Tables du Cadastre | 1–100,000 and 100,000–200,000 | 19 and 24, respectively | "seventeen enormous folios",[55] never published |
| 1794 | Jurij Vega Thesaurus Logarithmorum Completus (Leipzig) | corrected edition of Vlacq's work | ||
| 1795 | François Callet (Paris) | 100,000–108,000 | 7 | |
| 1871 | Sang | 1–200,000 | 7 |
Briggs and Vlacq also published original tables of the logarithms of the trigonometric functions.
Another critical application was the slide rule. The non-sliding logarithmic scale or Gunter's rule was invented by Edmund Gunter shortly after Napier's invention. This design was improved by William Oughtred into the slide rule: a pair of logarithmic scales movable with respect to each other. The slide rule was an essential calculating tool for engineers and scientists until the 1970s since it allows much faster computation than techniques based on tables.[51] The slide rule provides somewhat less precision than typical table-based calculations, but enough for many types of engineering.
See also
Notes
^ a: Some mathematicians disapprove of this notation. In his 1985 autobiography, Paul Halmos criticized what he considered the "childish ln notation," which he said no mathematician had ever used.[56]
In fact, the notation was invented by a mathematician Irving Stringham.[57][58]
References
- Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, World Scientific, ISBN 9789812560803, OCLC 492669517
- Shirali, Shailesh (2002), A Primer on Logarithms, Universities Press, ISBN 9788173714146
- ^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Technical Publications, ISBN 9788184317558, see Chapter 1
- ^ ""Mathematisches Lexikon" at Mateh_online.at".
- ^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, ISBN 978-0-7641-1972-9, chapter 17, p. 275
- ^ B. N. Taylor (1995). "Guide for the Use of the International System of Units (SI)". NIST Special Publication 811, 1995 Edition. US Department of Commerce.
- ^ Gullberg, Jan (1997), Mathematics: from the birth of numbers., W. W. Norton & Co, ISBN 039304002X
- ^ This notation was suggested by Edward Reingold and popularized by Donald Knuth[citation needed]
- ^ including C, C++, Java, Haskell, Fortran, Python, Ruby, and BASIC
- ^ Weisstein, Eric W. "Common Logarithm". MathWorld.
- ^ Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94841-6, MR1476913, section III.3
- ^ Lang 1997, section IV.2
- ^ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR1009558, see Section III.6
- ^ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5
- ^ Handbook of Mathematical Functions, National Bureau of Standards (Applied Mathematics Series no. 55), June 1964, page 68.
- ^ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, World Scientific, ISBN 9789810202460, see Section 1.2
- ^ Ganguly, S. (2005), Elements of Complex Analysis, Academic Publishers, ISBN 9788187504863, Definition 1.6.3
- ^ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, AMS Bookstore, ISBN 978-0-8218-4399-4, section 5.9
- ^ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, see page 135
- ^ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Cengage Learning, ISBN 978-0-547-15669-9, section 4.4.
- ^ IUPAC (1997), A. D. McNaught, A. Wilkinson (ed.), Compendium of Chemical Terminology ("Gold Book") (2nd ed.), Oxford: Blackwell Scientific Publications, doi:10.1351/goldbook, ISBN 0-9678550-9-8
- ^ Bakshi, U. A. (2009), Telecommunication Engineering, Technical Publications, ISBN 9788184317251, see Section 5.2
- ^ Maling, George C. (2007), "Noise", in Rossing, Thomas D. (ed.), Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, section 23.0.2
- ^ Bird, J. O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6, see section 34
- ^ Welford, A. T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, p. 61
- ^ Siegler, Robert S.; Opfer, John E. (2003), "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity", Psychological Science, 14 (3): 237–43, doi:10.1111/1467-9280.02438
- ^ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures", Science, 320 (5880): 1217–1220, doi:10.1126/science.1156540, PMC 2610411, PMID 18511690
- ^ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, see Chapter 19, p. 298
- ^ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, see section III.I
- ^ P. T. Bateman & Diamond 2004, Theorem 4.1
- ^ P. T. Bateman & Diamond 2004, Theorem 8.15
- ^ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, see Chapter 4
- ^ Aitchison, J.; Brown, J. A. C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935
- ^ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, R.I.: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5, see Section 2.1
- ^ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data" (PDF), Journal of Forensic Accounting, V: 17–34.
- ^ Wright, David (2009), Mathematics and music, AMS Bookstore, ISBN 978-0-8218-4873-9, see Chapter 5
- ^ Wooster, Woodruff B; Smith, David E (1902), Academic Algebra, Ginn & Company, p. 360
- ^ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, ISBN 978-0-486-61272-0, tenth printing, see section 4.7., p. 89
- ^ Silas Whitcomb Holman (1918), Computation Rules and Logarithms, Macmillan and Co.
- ^ Forrest M. Mims (2000), The Forrest Mims Circuit Scrapbook, Newnes, ISBN 1878707485
- ^ Bourbaki, Nicolas (1998), General topology. Chapters 5--10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, MR1726872, see section V.4.1
- ^ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4, see Section 1.4
- ^ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, vol. 20, Birkhäuser Verlag, ISBN 978-3-7643-2822-1, MR1193913, see section 2
- ^ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Cambridge University Press, ISBN 978-0-521-39231-0
- ^ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd ed.), London: CRC Press, ISBN 978-1-58488-508-5
- ^ Katok, Svetlana (2007), p-adic analysis compared with real, Student mathematical library, vol. 37, AMS Bookstore, ISBN 978-0-8218-4220-1, Section 3.4.1.
- ^ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, SIAM, ISBN 978-0-89871-646-7, see Chapter 11.
- ^ Gupta, R. C. (2000), "History of Mathematics in India", in Hoiberg, Dale; Ramchandani, Indu (eds.), Students' Britannica India: Select essays, Popular Prakashan, p. 329
- ^ Singh, A. N., Lucknow University http://www.jainworld.com/JWHindi/Books/shatkhandagama-4/02.htm
{{citation}}: Missing or empty|title=(help); Unknown parameter|unused_data=ignored (help) - ^ Walter William Rouse Ball (1908), A short account of the history of mathematics, Macmillan and Co, p. 216
- ^ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, 9780030776700, p. 182, ISBN 9780030776700
- ^ Ernest William Hobson. John Napier and the invention of logarithms. 1614. The University Press, 1914.
- ^ a b Maor 2009, section 1
- ^ Eves, Howard Whitley (1992), An introduction to the history of mathematics, The Saunders series (6th ed.), Philadelphia: Saunders, ISBN 978-0-03-029558-4, section 9-3
- ^ Maor 2009, section 2
- ^ "this cannot be regarded as a great number, when it is considered that the table was the result of an original calculation, and that more than 2,100,000 printed figures are liable to error.", Athenaeum, 15 June 1872. See also the Monthly Notices of the Royal Astronomical Society for May 1872.
- ^ English Cyclopaedia, Biography, Vol. IV., article "Prony."
- ^ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Springer-Verlag, ISBN 978-0387960784
- ^ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii
- ^ Roy S. Freedman (2006), Introduction to Financial Technology, Academic Press, p. 59, ISBN 9780123704788
External links
- Logarithms on geoset.info
- Jost Burgi, Swiss Inventor of Logarithms
- Translation of Napier's work on logarithms
- Algorithm for determining Log values for any base





![{\displaystyle \log _{b}({\sqrt[{p}]{x}})={\frac {\log _{b}(x)}{p}}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc3bd89e2a1789064418e0f8c68c4f3b48fcbe01)












![{\displaystyle {\begin{aligned}-\ln(1-x)&=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{\frac {x^{4}}{4}}+\cdots \\[6pt]\ln(1-x)&=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}-\cdots .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45a5693660b875be375fe86ff091e87128d4350)







![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)

![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\cdot \log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f66dd86aabb1bcc6a3772f0ba3f52ca3f12bea7)
![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\cdot \log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3501339845305ee5f05ca0d776c687e933a5cc8d)


![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01417eed9495836c4b9545de6df92b6bd7abe388)

