Normal distribution

This article is about the univariate normal distribution. For normally distributed vectors, see Multivariate normal distribution. For matrices, see Matrix normal distribution. For stochastic processes, see Gaussian process.

Probability density function 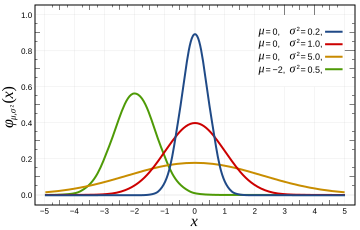The red line is the standard normal distribution
Cumulative distribution function Colors match the image above
Parameters	μ ∈ R — location (real) σ2 > 0 — squared scale (real)
Support	x ∈ R
PDF	${\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)$
CDF	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \!\left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)$
Mean	μ
Median	μ
Mode	μ
Variance	σ2
Skewness	0
Excess kurtosis	0
Entropy	$\ln \!{\sqrt {2\pi \sigma ^{2}e}}$
MGF	$\exp \!{\Big (}\mu t+{\tfrac {1}{2}}\sigma ^{2}t^{2}{\Big )}$
CF	$\exp \!{\Big (}i\mu t-{\tfrac {1}{2}}\sigma ^{2}t^{2}{\Big )}$

In probability theory and statistics, the normal distribution or Gaussian distribution is a continuous probability distribution that describes data that cluster around a mean or average. The graph of the associated probability density function is bell-shaped, with a peak at the mean, and is known as the Gaussian function or bell curve. The Gaussian distribution is one of many things named after Carl Friedrich Gauss, who used it to analyze astronomical data, and determined the formula for its probability density function. However, Gauss was not the first to study this distribution or the formula for its density function—that had been done earlier by Abraham de Moivre.

The normal distribution can be used to describe, at least approximately, any variable that tends to cluster around the mean. For example, the heights of adult males in the United States are roughly normally distributed, with a mean of about 70 in (1.8 m). Most men have a height close to the mean, though a small number of outliers have a height significantly above or below the mean. A histogram of male heights will appear similar to a bell curve, with the correspondence becoming closer if more data are used.

By the central limit theorem, the sum of a large number of independent random variables is distributed approximately normally. For this reason, the normal distribution is used throughout statistics, natural science, and social science as a simple model for complex phenomena. For example, the observational error in an experiment is usually assumed to follow a normal distribution, and the propagation of uncertainty is computed using this assumption.

History

The Galton board is a device invented by Sir Francis Galton with the purpose to demonstrate how the normal distribution appears in nature. This machine consists of a vertical board with interleaved rows of pins. Small balls are dropped from the top and then bounce randomly left or right as they hit the pins. The balls are collected into bins at the bottom and settle down into the pattern approximating the Gaussian curve.

The normal distribution was first introduced by Abraham de Moivre in an article in 1733, which was reprinted in the second edition of his “The Doctrine of Chances” (1738) in the context of approximating certain binomial distributions for large n. His result was extended by Laplace in his book “Analytical theory of probabilities” (1812), and is now called the theorem of de Moivre–Laplace.

Laplace used the normal distribution in the analysis of errors of experiments. The important method of least squares was introduced by Legendre in 1805. Gauss, who claimed to have used the method since 1794, justified it rigorously in 1809 by assuming a normal distribution of the errors.

Since its introduction, the normal distribution has been known by many different names: the law of error, the law of facility of errors, Laplace’s second law, Gaussian law, etc. Curiously, it has never been known under the name of its inventor, de Moivre. The name “normal distribution” was coined independently by Peirce, Galton and Lexis around 1875; the term was derived from the fact that this distribution was seen as typical, common, normal. This name “normal distribution” was popularized in statistical community by Karl Pearson around the turn of the 20th century.

The term “standard normal” which denotes the normal distribution with zero mean and unit variance came into general use around 1950s, appearing in the popular textbooks by P.G. Hoel (1947) “Introduction to mathematical statistics” and A.M. Mood (1950) “Introduction to the theory of statistics”.

Definition

In its simplest form, normal distribution can be described by the probability density function

$\phi (x)={\tfrac {1}{\sqrt {2\pi }}}\,e^{-\,x^{2}\!/2}$

which is known as the standard normal distribution. The constant $\scriptstyle 1/{\sqrt {2\pi }}$ in this expression ensures that the area under the curve ϕ(x) is equal to 1. This fact can be proved using simple calculus. Note that it is standard in statistics to denote the pdf of a standard normal random variable with the greek letter ϕ, whereas density functions for other distributions are usually denoted with letters ƒ or p.

Standard normal distribution is centered around point x = 0, and has the “width” of the curve equal to 1. Generally we consider the normal distribution with arbitrary center μ, and variance σ². The probability density function for such distribution is given by the formula

$f(x)={\tfrac {1}{\sqrt {2\pi \sigma ^{2}}}}\,e^{-(x-\mu )^{2}/(2\sigma ^{2})}={\tfrac {1}{\sigma }}\,\phi {\big (}{\tfrac {x-\mu }{\sigma }}{\big )}$

Parameter μ is called the mean, and it determines the location of the peak of the density function. Point x = μ is at the same time the mean, the median and the mode of normal distribution. Parameter σ is called standard deviation, and σ² is the variance of the distribution. Some authors instead of σ² use its reciprocal τ = σ⁻², which is called the precision. This parameterization has an advantage in numerical applications where σ² is very close to zero and is more convenient to work with in analysis as τ is a natural parameter of the normal distribution.

In this article we assume that σ is strictly greater than zero. While it is certainly useful for certain limit theorems (e.g. asymptotic normality of estimators) and for the theory of Gaussian processes to consider the probability distribution concentrated at μ (see Dirac measure) as a normal distribution with mean μ and variance σ² = 0, this degenerate case is often excluded from the considerations because no density with respect to the Lebesgue measure exists without the use of generalized functions.

Normal distribution is denoted as N(μ,σ²), sometimes the letter N is written in calligraphic font (typed as \mathcal{N} in LaTeX). Thus when a random variable X is distributed normally with mean μ and variance σ², we write

$X\sim {\mathcal {N}}(\mu ,\,\sigma ^{2}).\,$

Characterization

In the definition section we defined the normal distribution by specifying its probability density function. However this is just one of the possible ways to characterize a probability distribution. Other ways include the cumulative distribution function, the moments, the cumulants, the characteristic function, the moment-generating function, etc.

Probability density function

The continuous probability density function of the normal distribution is the Gaussian function

$f(x;\,\mu ,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-(x-\mu )^{2}/(2\sigma ^{2})}={\tfrac {1}{\sigma }}\,\phi {\big (}{\tfrac {x-\mu }{\sigma }}{\big )},\ x\in \mathbb {R} ,$

where σ > 0 is the standard deviation, the real parameter μ is the expected value, and ϕ(x) = (2π)^−1/2e^−x2/2 is the density of the “standard normal” distribution, i.e. the normal distribution with μ = 0 and σ = 1. The integral of ƒ(x; μ, σ²) over the real line is equal to one as shown in the Gaussian integral article.

Properties:

• function ƒ is symmetric around x = μ;
• the mode, median and mean are all equal to the location parameter μ;
• the inflection points of the curve occur one standard deviation away from the mean (i.e., at μ − σ and μ + σ);
• the function is supersmooth of order 2, implying that it is infinitely differentiable;
• the standard normal density function ϕ is an eigenfunction of the Fourier transform;
• the derivative of ϕ is ϕ′(x) = −xϕ(x), the second derivative is ϕ′′(x) = (x²−1)ϕ(x).

Cumulative distribution function

The cumulative distribution function (cdf) of a random variable X evaluated at a number x, is the probability of the event that X is less than or equal to x. The cdf of the standard normal distribution is denoted with the capital greek letter Φ (phi), and can be computed as an integral of the probability density function:

$\Phi (x)=\int _{-\infty }^{x}\phi (t)\,dt={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt.$

This integral cannot be expressed in terms of standard functions, however with the use of a special function erf, called the error function, the standard normal cdf Φ(x) can be written as

$\Phi (x)={\frac {1}{2}}{\Big [}1+\operatorname {erf} {\Big (}{\frac {x}{\sqrt {2}}}{\Big )}{\Big ]},\quad x\in \mathbb {R} .$

The complement of the standard normal cdf, 1 − Φ(x), is often denoted Q(x), and is referred to as the Q-function, especially in engineering texts. This represents the tail probability of the Gaussian distribution, that is the probability that a standard normal random variable X is greater than the number x:

$Q(x)=\int _{x}^{\infty }\phi (t)\,dt=1-\Phi (x).$

Other definitions of the Q-function, all of which are simple transformations of Φ, are also used occasionally.

The inverse of the standard normal cdf, called the quantile function or probit function, can be expressed in terms of the inverse error function:

$\Phi ^{-1}(z)={\sqrt {2}}\,\operatorname {erf} ^{-1}(2z-1),\quad z\in (0,1).$

It is recommended to use letter z to denote the quantiles of the standard normal cdf, unless that letter is already used for some other purpose.

The values Φ(x) may be approximated very accurately by a variety of methods, such as numerical integration, Taylor series, asymptotic series and continued fractions. For large values of x it is usually easier to work with the Q-function.

For a generic normal random variable with mean μ and variance σ² the cdf will be equal to

$F(x;\,\mu ,\sigma ^{2})=\int _{-\infty }^{x}f(t;\mu ,\sigma ^{2})\,dt=\Phi {\big (}{\tfrac {x-\mu }{\sigma }}{\big )}={\frac {1}{2}}{\Big [}1+\operatorname {erf} {\Big (}{\frac {x-\mu }{\sigma {\sqrt {2}}}}{\Big )}{\Big ]},\quad x\in \mathbb {R}$

and the corresponding quantile function is

$F^{-1}(p;\,\mu ,\sigma ^{2})=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

Properties:

• the standard normal cdf is symmetric around point (0, ½): Φ(−x) = 1 − Φ(x);
• the derivative of Φ is equal to the pdf ϕ: Φ’(x) = ϕ(x);
• the antiderivative of Φ is: ∫ Φ(x) dx = xΦ(x) + ϕ(x).

Characteristic function

The characteristic function φ_X(t) of a random variable X is defined as the expected value of e^itX, where i is the imaginary unit, and t ∈ R is the argument of the characteristic function. Thus the characteristic function is the Fourier transform of the density ϕ(x).

For the standard normal random variable, the characteristic function is

$\varphi (t)=\int _{-\infty }^{\infty }e^{itx}{\tfrac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}dx=e^{-{\frac {1}{2}}t^{2}}.$

For a generic normal distribution with mean μ and variance σ², the characteristic function is

$\varphi (t;\,\mu ,\sigma ^{2})=\operatorname {E} [e^{it{\mathcal {N}}(\mu ,\sigma ^{2})}]=e^{i\mu t-{\frac {1}{2}}\sigma ^{2}t^{2}}.$

Moment generating function

The moment generating function is defined as the expected value of e^tX. For a normal distribution, the moment generating function exists and is equal to

$M(t;\,\mu ,\sigma ^{2})=\operatorname {E} [e^{tX}]=\chi (-it;\,\mu ,\sigma ^{2})=e^{\mu t+{\frac {1}{2}}\sigma ^{2}t^{2}}.$

The cumulant generating function is the logarithm of the moment generating function:

$g(t;\,\mu ,\sigma ^{2})=\ln M(t;\,\mu ,\sigma ^{2})=\mu t+{\tfrac {1}{2}}\sigma ^{2}t^{2}$

Since this is a quadratic polynomial in t, only the first two cumulants are nonzero.

Properties

The joint distribution of two independent normal random variables is a special case of the bivariate normal distribution.

1. The family of normal distributions is closed under linear transformations. That is, if X is normally distributed with mean μ and variance σ², then a linear transform aX + b (for some real numbers a≠0 and b) is also normally distributed:

   $aX+b\ \sim \ {\mathcal {N}}(a\mu +b,\,a^{2}\sigma ^{2}).$

   Also if X₁, X₂ are two independent normal random variables, with means μ₁, μ₂ and standard deviations σ₁, σ₂, then their linear combination will also be normally distributed: ^[proof]

   $aX_{1}+bX_{2}\ \sim \ {\mathcal {N}}(a\mu _{1}+b\mu _{2},\,a^{2}\!\sigma _{1}^{2}+b^{2}\sigma _{2}^{2})$

2. The converse of (1) is also true: if X₁ and X₂ are independent and their sum X₁ + X₂ is distributed normally, then both X₁ and X₂ must also be normal. This is known as the Cramér’s theorem.
3. Normal distribution is infinitely divisible: for a normally distributed X with mean μ and variance σ² we can find n independent random variables {X₁, …, X_n} each distributed normally with means μ/n and variances σ²/n such that

   $X_{1}+X_{2}+\cdots +X_{n}\ \sim \ {\mathcal {N}}(\mu ,\sigma ^{2})$

4. Normal distribution is stable (with exponent α = 2): if X₁, X₂ are two independent N(μ,σ²) random variables and a, b are arbitrary real numbers, then

   $aX_{1}+bX_{2}\ \sim \ {\sqrt {a^{2}+b^{2}}}\cdot X_{3}\ +\ (a+b-{\sqrt {a^{2}+b^{2}}})\mu ,$

   where X₃ is also N(μ,σ²). This relationship directly follows from property (1).
5. The Kullback–Leibler divergence between two normal distributions X₁ ∼ N(μ₁, σ²₁) and X₂ ∼ N(μ₂, σ²₂) is given by:

   $D_{\rm {KL}}(X_{1}\|X_{2})=\ln \!{\bigg (}{\frac {\sigma _{2}}{\sigma _{1}}}{\bigg )}\,+\,{\frac {\sigma _{1}^{2}+(\mu _{1}-\mu _{2})^{2}}{2\sigma _{2}^{2}}}\,-\,{\frac {1}{2}}\ .$

   The Hellinger distance between the same distributions is equal to

   $H(X_{1},X_{2})=\left(1-{\sqrt {\frac {2\sigma _{1}\sigma _{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}}\,e^{-{\frac {1}{4}}{\frac {(\mu _{1}-\mu _{2})^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}}\right)^{\!1/2}.$

6. Normal distributions form a two-parameter exponential family with natural parameters μ and $\scriptstyle {\frac {1}{\sigma ^{2}}}$, and natural statistics X and X². The canonical form has parameters $\scriptstyle {\mu \over \sigma ^{2}}$ and $\scriptstyle {1 \over \sigma ^{2}}$ and sufficient statistics $\scriptstyle \sum x$ and $\scriptstyle -{1 \over 2}\sum x^{2}.$

Standardizing normal random variables

As a consequence of property 1, it is possible to relate all normal random variables to the standard normal. For example if X is normal with mean μ and variance σ², then

$Z={\frac {X-\mu }{\sigma }}$

has mean zero and unit variance, that is Z has the standard normal distribution. Conversely, having a standard normal random variable Z we can always construct another normal random variable with specific mean μ and variance σ²:

$X=\sigma Z+\mu .\,$

This “standardizing” transformation is convenient as it allows one to compute the pdf and especially the cdf of a normal distribution having the table of pdf and cdf values for the standard normal. They will be related via

$F_{X}(x)=\Phi {\bigg (}{\frac {x-\mu }{\sigma }}{\bigg )},\quad f_{X}(x)={\frac {1}{\sigma }}\,\phi {\bigg (}{\frac {x-\mu }{\sigma }}{\bigg )}.$

Moments

The normal distribution has moments of all orders. That is, for a normally distributed X with mean μ and variance σ², the expectation E[|X|^p] exists and is finite for all p such that Re[p]>−1. Usually we are interested only in moments of integer orders: p = 1, 2, 3, ….

• Central moments are the moments of X around its mean μ. Thus, central moment of order p is the expected value of (X−μ)^p. Using standardization of normal distribution, this expectation will be equal to σ^pE[Z^p], where Z is standard normal.

  $\operatorname {E} {\big [}(X-\mu )^{p}{\big ]}={\begin{cases}0&{\text{if }}p{\text{ odd}}\\\sigma ^{p}(p-1)!!&{\text{if }}p{\text{ even}}\end{cases}}=\sigma ^{p}{\frac {p!}{2^{p/2}(p/2)!}}\cdot \mathbf {1} _{\{p{\text{ even}}\}}.$

  Here n!! denotes the double factorial, that is the product of every other number from n to 1; and 1_{…} is the indicator function.
• Central absolute moments are the moments of |X−μ|. They coincide with regular moments for all even orders, but are nonzero for all odd p’s.

  $\operatorname {E} {\big [}|X-\mu |^{p}{\big ]}=\sigma ^{p}(p-1)!!\cdot {\begin{cases}{\sqrt {2/\pi }}&{\text{if }}p{\text{ odd}}\\1&{\text{if }}p{\text{ even}}\end{cases}}.$

• Raw moments and raw absolute moments are the moments of X and |X| respectively. The formulas for these moments are much more complicated, and are given in terms of confluent hypergeometric functions ₁F₁ and U.

  ${\begin{aligned}&\operatorname {E} {\big [}X^{p}{\big ]}=\sigma ^{p}\cdot (-i{\sqrt {2}}\operatorname {sgn} \mu )^{p}\;U{\Big (}{-{\tfrac {1}{2}}p},\,{\tfrac {1}{2}},\,-{\tfrac {1}{2}}(\mu /\sigma )^{2}{\Big )},\\&\operatorname {E} {\big [}|X|^{p}{\big ]}=\sigma ^{p}\cdot 2^{\frac {p}{2}}{\frac {\Gamma {\big (}{\frac {1+p}{2}}{\big )}}{\sqrt {\pi }}}\;_{1}F_{1}{\Big (}{-{\tfrac {1}{2}}p},\,{\tfrac {1}{2}},\,-{\tfrac {1}{2}}(\mu /\sigma )^{2}{\Big )}.\\\end{aligned}}$

  These expressions remain valid even if p is not integer.
• First two cumulants are equal to μ and σ² respectively, whereas all higher-order cumulants are equal to zero.

Order	Raw moment	Central moment	Cumulant
1	$\scriptstyle \mu$	0	$\scriptstyle \mu$
2	$\scriptstyle \mu ^{2}+\sigma ^{2}$	$\scriptstyle \sigma ^{2}$	$\scriptstyle \sigma ^{2}$
3	$\scriptstyle \mu ^{3}+3\mu \sigma ^{2}$	0	0
4	$\scriptstyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}$	$\scriptstyle 3\sigma ^{4}$	0
5	$\scriptstyle \mu ^{5}+10\mu ^{3}\sigma ^{2}+15\mu \sigma ^{4}$	0	0
6	$\scriptstyle \mu ^{6}+15\mu ^{4}\sigma ^{2}+45\mu ^{2}\sigma ^{4}+15\sigma ^{6}$	$\scriptstyle 15\sigma ^{6}$	0
7	$\scriptstyle \mu ^{7}+21\mu ^{5}\sigma ^{2}+105\mu ^{3}\sigma ^{4}+105\mu \sigma ^{6}$	0	0
8	$\scriptstyle \mu ^{8}+28\mu ^{6}\sigma ^{2}+210\mu ^{4}\sigma ^{4}+420\mu ^{2}\sigma ^{6}+105\sigma ^{8}$	$\scriptstyle 105\sigma ^{8}$	0

Central limit theorem

Main article: central limit theorem

Plot of the pdf of a normal distribution with μ = 12 and σ = 3, approximating the pdf of a binomial distribution with n = 48 and p = 1/4

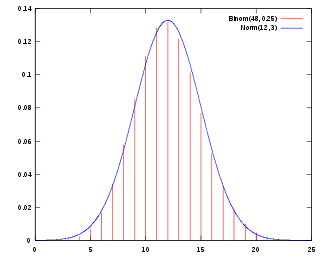
Under certain conditions (such as being independent and identically-distributed with finite variance), the sum of a large number of random variables is approximately normally distributed; this is the central limit theorem.

The practical importance of the central limit theorem is that the normal cumulative distribution function can be used as an approximation to some other cumulative distribution functions, for example:

• A binomial distribution with parameters n and p is approximately normal for large n and p not too close to 1 or 0 (some books recommend using this approximation only if np and n(1 − p) are both at least 5; in this case, a continuity correction should be applied).
  The approximating normal distribution has parameters μ = np, σ² = np(1 − p).
• A Poisson distribution with parameter λ is approximately normal for large λ.
  The approximating normal distribution has parameters μ = σ² = λ.

Whether these approximations are sufficiently accurate depends on the purpose for which they are needed, and the rate of convergence to the normal distribution. It is typically the case that such approximations are less accurate in the tails of the distribution. A general upper bound of the approximation error of the cumulative distribution function is given by the Berry–Esséen theorem.

Standard deviation and confidence intervals

Dark blue is less than one standard deviation from the mean. For the normal distribution, this accounts for about 68% of the set (dark blue), while two standard deviations from the mean (medium and dark blue) account for about 95%, and three standard deviations (light, medium, and dark blue) account for about 99.7%.

About 68% of values drawn from a normal distribution are within one standard deviation σ > 0 away from the mean μ; about 95% of the values are within two standard deviations and about 99.7% lie within three standard deviations. This is known as the 68-95-99.7 rule, or the empirical rule, or the 3-sigma rule.

To be more precise, the area under the bell curve between μ − nσ and μ + nσ in terms of the cumulative normal distribution function is given by

${\begin{aligned}&F(\mu +n\sigma ;\,\mu ,\sigma ^{2})-F(\mu -n\sigma ;\,\mu ,\sigma ^{2})\\&\quad =\Phi (n)-\Phi (-n)=2\Phi (n)-1=\mathrm {erf} \left({\frac {n}{\sqrt {2}}}\right),\end{aligned}}$

where erf is the error function. To 12 decimal places, the values for the 1-, 2-, up to 6-sigma points are:

$\scriptstyle \;n\;$	$\;\scriptstyle \mathrm {erf} \left({\frac {n}{\sqrt {2}}}\right)\;$
1	0.682689492137
2	0.954499736104
3	0.997300203937
4	0.999936657516
5	0.999999426697
6	0.999999998027

The next table gives the reverse relation of sigma multiples corresponding to a few often used values for the area under the bell curve. These values are useful to determine (asymptotic) confidence intervals of the specified levels based on normally distributed (or asymptotically normal) estimators:

$\scriptstyle \;\mathrm {erf} \left({\frac {n}{\sqrt {2}}}\right)\;$	$\scriptstyle \;n\;$
0.80	1.281551565545
0.90	1.644853626951
0.95	1.959963984540
0.98	2.326347874041
0.99	2.575829303549
0.995	2.807033768344
0.998	3.090232306168
0.999	3.290526731492
0.9999	3.890591886413
0.99999	4.417173413469

where the value on the left of the table is the proportion of values that will fall within a given interval and n is a multiple of the standard deviation that specifies the width of the interval.

Related and derived distributions

• If X is distributed normally with mean μ and variance σ², then
  • The exponent of X is distributed log-normally: e^X ~ Ln-N(μ, σ²).
  • The absolute value of X has folded normal distribution: IXI ~ N_f (μ, σ²).
  • The square of X, scaled down by the variance σ², has the non-central chi-square distribution with 1 degree of freedom: X²/σ² ~ χ²₁(μ). If μ = 0, the distribution is called simply chi-square.
  • Variable X restricted to an interval [a, b] is called the truncated normal distribution.
• If X₁ and X₂ are two independent standard normal random variables, then
  • Their sum and difference is distributed normally with mean zero and variance two: X₁ ± X₂ ∼ N(0, 2).
  • Their product Z = X₁ · X₂ follows an (unnamed?) distribution with density function

    $f_{Z}(z)=\pi ^{-1}K_{0}(|z|),\,$

    where K₀ is the modified Bessel function of the second kind. This distribution is symmetric around zero, unbounded at z = 0, and has the characteristic function φ_Z(t) = (1 + t²)^−1/2.
  • Their ratio follows the standard Cauchy distribution: X₁ ÷ X₂ ∼ Cauchy(0, 1).
  • Their Euclidean norm has the Rayleigh distribution (also known as chi distribution with 2 degrees of freedom):

    $\textstyle {\sqrt {X_{1}^{2}+X_{2}^{2}}}\ \sim \ {\text{Rayleigh}}(1).$

• If X₁, X₂, …, X_n are independent standard normal random variables, then the sum of their squares has the chi-square distribution with n degrees of freedom: $\scriptstyle X_{1}^{2}+\ldots +X_{n}^{2}\ \sim \ \chi _{n}^{2}$.
• If X₁, X₂, …, X_n are independent normally distributed random variables with means μ and variances σ², then their sample mean is independent from the sample standard deviation, which can be demonstrated using the Basu’s theorem or Cochran’s theorem. The ratio of these two quantities will have the Student’s t-distribution with n − 1 degrees of freedom:

  $t={\frac {\overline {X}}{S}}={\frac {{\tfrac {1}{n}}(X_{1}+\ldots +X_{n})}{\sqrt {{\tfrac {1}{n-1}}{\big [}(X_{1}-{\overline {X}})^{2}+\ldots +(X_{n}-{\overline {X}})^{2}{\big ]}}}}\ \sim \ t_{n-1}$

Descriptive and inferential statistics

Scores

Many scores are derived from the normal distribution, including percentile ranks ("percentiles" or "quantiles"), normal curve equivalents, stanines, z-scores, and T-scores. Additionally, a number of behavioral statistical procedures are based on the assumption that scores are normally distributed; for example, t-tests and ANOVAs (see below). Bell curve grading assigns relative grades based on a normal distribution of scores.

Normality tests

Main article: normality test

Normality tests check a given set of data for similarity to the normal distribution. The null hypothesis is that the data set is similar to the normal distribution, therefore a sufficiently small P-value indicates non-normal data.

• Kolmogorov–Smirnov test
• Lilliefors test
• Anderson–Darling test
• Ryan–Joiner test
• Shapiro–Wilk test
• Normal probability plot (rankit plot)
• Jarque–Bera test
• Spiegelhalter's omnibus test

Estimation of parameters

Estimators

Main articles: standard error of the mean and unbiased estimation of standard deviation

For a normal distribution with mean μ and variance σ², the sample mean $\scriptstyle {\overline {X}}$:

• is the UMVU estimator for the population mean μ, by the Lehmann–Scheffé theorem (because it is an unbiased, complete, sufficient statistic),
• is the maximum likelihood estimator for the population mean μ,
• has sampling distribution $\scriptstyle N(\mu ,\sigma ^{2}/n),$ since the sum of n i.i.d. random variables has distribution $\scriptstyle N(n\mu ,n\sigma ^{2}),$ and thus
• the standard error of the sample mean is $\scriptstyle \sigma /{\sqrt {n}}$.

As the number of samples grows, the standard error of the sample mean decays as $\scriptstyle {\frac {1}{\sqrt {n}}}$, so if one wishes to decrease the standard error by a factor of 10, one must increase the number of samples by a factor of 100. This fact is widely used in determining sample sizes for opinion polls and number of trials in Monte Carlo simulation.

The sample distribution of the mean depends on the standard deviation σ; it is not an ancillary statistic, and thus to estimate the error of the sample mean, one must estimate the standard deviation.

The sample standard deviation, defined as:

$s={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}},$

is a common estimator for the population standard deviation:

• $\scriptstyle s^{2}$ is an unbiased estimator for the variance σ²,
• the sampling distribution of s² is, up to scale, a chi-square distribution with n–1 degrees of freedom;
• properly, $\scriptstyle {\frac {(n-1)s_{n}^{2}}{\sigma ^{2}}}\,\sim \,\chi _{n-1}^{2};$
• s is an ancillary statistic of the population mean μ; its sampling distribution does not depend on the population mean, and
• s² (and thus s) are independent of the sample mean $\scriptstyle {\overline {X}}$, by Cochran's theorem.

Correction factor c₄ in unbiased estimation of standard deviation of a normal distribution.

Note that:

• There is a factor of n–1, not n, in the definition; this corresponds to the number of degrees of freedom (the residuals sum to 1, which removes one degree of freedom), and is known as Bessel's correction.
• The normal distribution is the only distribution whose sample mean and sample variance are independent.
• While $\scriptstyle s^{2}$ is an unbiased estimator for the variance σ², s is a biased estimator for the standard deviation σ; see unbiased estimation of standard deviation.

For the normal distribution, one can compute a correction factor, which depends on n, to arrive at an unbiased estimator of the standard deviation. This is denoted by c₄, and the corrected (unbiased) estimator is $\scriptstyle {\frac {s}{c_{4}}}$. For n=2 $\scriptstyle c_{4}\,\approx \,0.80$, while for n=10 $\scriptstyle c_{4}\,\approx \,0.97,$ so this correction is rarely used outside of high-precision estimation of small samples.

The standard error of the uncorrected (biased) sample standard deviation s is $\scriptstyle \sigma {\sqrt {1-c_{4}^{2}}}\,\approx \,\sigma /{\sqrt {2n}},$ thus it also decays as $\scriptstyle {\frac {1}{\sqrt {n}}}$.

Unbiased estimation of parameters

The maximum likelihood estimator of the population mean μ from a sample is an unbiased estimator of the mean. The maximum likelihood estimator of the variance is unbiased if we assume the population is known a priori, but in practice that does not happen. However, if we are faced with a sample and have no knowledge of the mean or the variance of the population from which it is drawn, as assumed in the maximum likelihood derivation above, then the maximum likelihood estimator of the variance is biased. An unbiased estimator of the variance σ² is:

$S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}.$

This "sample variance" follows a Gamma distribution if all X_i are independent and identically-distributed:

$S^{2}\sim \Gamma \left({\frac {n-1}{2}},{\frac {2\sigma ^{2}}{n-1}}\right),$

with mean $\scriptstyle \operatorname {E} (S^{2})\,=\,\sigma ^{2}$ and variance $\scriptstyle \operatorname {Var} (S^{2})\,=\,{\frac {2\sigma ^{4}}{n-1}}.$

The maximum likelihood estimate of the standard deviation is the square root of the maximum likelihood estimate of the variance. However, neither this nor the square root of the sample variance provides an unbiased estimate for standard deviation: see unbiased estimation of standard deviation for formulae particular to the normal distribution.

Maximum likelihood estimation of parameters

Suppose

$X_{1},\dots ,X_{n}$

are independent and each is normally distributed with expectation μ and variance σ ² > 0. In the language of statisticians, the observed values of these n random variables make up a "sample of size n from a normally distributed population." It is desired to estimate the "population mean" μ and the "population standard deviation" σ, based on the observed values of this sample. The continuous joint probability density function of these n independent random variables is

${\begin{aligned}f(x_{1},\dots ,x_{n};\mu ,\sigma )&=\prod _{i=1}^{n}\phi _{\mu ,\sigma ^{2}}(x_{i})\\&={\frac {1}{(\sigma {\sqrt {2\pi }})^{n}}}\prod _{i=1}^{n}\exp {\biggl (}-{1 \over 2}{\Bigl [}{x_{i}-\mu \over \sigma }{\Bigr ]}^{2}{\biggr )},\;(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}.\end{aligned}}$

As a function of μ and σ, the likelihood function based on the observations X₁, ..., X_n is

$L(\mu ,\sigma )={\dfrac {C}{\sigma ^{n}}}\exp \left(-{\sum _{i=1}^{n}(X_{i}-\mu )^{2} \over 2\sigma ^{2}}\right),\;\mu \in \mathbb {R} ,\ \sigma >0,$

with some constant C > 0 (which in general would be even allowed to depend on X₁, ..., X_n, but will vanish anyway when partial derivatives of the log-likelihood function with respect to the parameters are computed, see below).

In the method of maximum likelihood, the values of μ and σ that maximize the likelihood function are taken as estimates of the population parameters μ and σ.

Usually in maximizing a function of two variables, one might consider partial derivatives. But here we will exploit the fact that the value of μ that maximizes the likelihood function with σ fixed does not depend on σ. Therefore, we can find that value of μ, then substitute it for μ in the likelihood function, and finally find the value of σ that maximizes the resulting expression.

It is evident that the likelihood function is a decreasing function of the sum

$\sum _{i=1}^{n}(X_{i}-\mu )^{2}.\,\!$

So we want the value of μ that minimizes this sum. Let

${\overline {X}}_{n}={\frac {1}{n}}(X_{1}+\cdots +X_{n})$

be the "sample mean" based on the n observations. Observe that

${\begin{aligned}\sum _{i=1}^{n}(X_{i}-\mu )^{2}&=\sum _{i=1}^{n}{\bigl (}[X_{i}-{\overline {X}}_{n}]+({\overline {X}}_{n}-\mu ){\bigr )}^{2}\\&=\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}+2({\overline {X}}_{n}-\mu )\underbrace {\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})} _{=\,0}+\sum _{i=1}^{n}({\overline {X}}_{n}-\mu )^{2}\\&=\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}+n({\overline {X}}_{n}-\mu )^{2}.\end{aligned}}$

Only the last term depends on μ and it is minimized by

${\widehat {\mu }}_{n}={\overline {X}}_{n}.$

That is the maximum-likelihood estimate of μ based on the n observations X₁, ..., X_n. When we substitute that estimate for μ into the likelihood function, we get

$L({\overline {X}}_{n},\sigma )={\frac {C}{\sigma ^{n}}}\exp {\biggl (}-{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over 2\sigma ^{2}}{\biggr )},\;\sigma >0.$

It is conventional to denote the log-likelihood function (i.e., the logarithm of the likelihood function, by a lower-case ℓ) and we have

$\ell ({\overline {X}}_{n},\sigma )=\log C-n\log \sigma -{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over 2\sigma ^{2}},\;\sigma >0,$

and then

${\begin{aligned}{\partial \over \partial \sigma }\ell ({\overline {X}}_{n},\sigma )&=-{n \over \sigma }+{\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2} \over \sigma ^{3}}\\&=-{n \over \sigma ^{3}}{\biggl (}\sigma ^{2}-{1 \over n}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}{\biggr )},\;\sigma >0.\end{aligned}}$

This derivative is positive, zero, or negative according as σ² is between 0 and

${\hat {\sigma }}_{n}^{2}:={1 \over n}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2},$

or equal to that quantity, or greater than that quantity. (If there is just one observation, meaning that n = 1, or if X₁ = ... = X_n, which only happens with probability zero, then $\scriptstyle {\hat {\sigma }}{}_{n}^{2}\,=\,0$ by this formula, reflecting the fact that in these cases the likelihood function is unbounded as σ decreases to zero.)

Consequently this average of squares of residuals is the maximum-likelihood estimate of σ², and its square root is the maximum-likelihood estimate of σ based on the n observations. This estimator $\scriptstyle {\hat {\sigma }}{}_{n}^{2}$ is biased, but has a smaller mean squared error than the usual unbiased estimator, which is $\scriptstyle {\frac {n}{n-1}}$ times this estimator.

Surprising generalization

The derivation of the maximum-likelihood estimator of the covariance matrix of a multivariate normal distribution is subtle. It involves the spectral theorem and the reason it can be better to view a scalar as the trace of a 1×1 matrix than as a mere scalar. See estimation of covariance matrices.

Occurrence

Approximately normal distributions occur in many situations, as explained by the central limit theorem. When there is reason to suspect the presence of a large number of small effects acting additively and independently, it is reasonable to assume that observations will be normal. There are statistical methods to empirically test that assumption, for example the Kolmogorov–Smirnov test.

Effects can also act as multiplicative (rather than additive) modifications. In that case, the assumption of normality is not justified, and it is the logarithm of the variable of interest that is normally distributed. The distribution of the directly observed variable is then called log-normal.

Finally, if there is a single external influence which has a large effect on the variable under consideration, the assumption of normality is not justified either. This is true even if, when the external variable is held constant, the resulting marginal distributions are indeed normal. The full distribution will be a superposition of normal variables, which is not in general normal. This is related to the theory of errors (see below).

To summarize, here is a list of situations where approximate normality is sometimes assumed. For a fuller discussion, see below.

• In counting problems, where the central limit theorem includes a discrete-to-continuum approximation and where infinitely divisible and decomposable distributions are involved, such as
  • Binomial random variables, associated with yes/no questions;
  • Poisson random variables, associated with rare events;
• In physiological measurements of biological specimens:
  • The logarithm of measures of size of living tissue (length, height, skin area, weight);
  • The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth; presumably the thickness of tree bark also falls under this category;
  • Other physiological measures may be normally distributed, but there is no reason to expect that a priori;
• Measurement errors are often assumed to be normally distributed, and any deviation from normality is considered something which should be explained;
• Financial variables, in the Black–Scholes model
  • Changes in the logarithm of exchange rates, price indices, and stock market indices; these variables behave like compound interest, not like simple interest, and so are multiplicative;
  • While the Black–Scholes model assumes normality, in reality these variables exhibit heavy tails, as seen in stock market crashes;
  • Other financial variables may be normally distributed, but there is no reason to expect that a priori;
• Light intensity
  • The intensity of laser light is normally distributed;
  • Thermal light has a Bose–Einstein distribution on very short time scales, and a normal distribution on longer timescales due to the central limit theorem.

Of relevance to biology and economics is the fact that complex systems tend to display power laws rather than normality.

Photon counting

Light intensity from a single source varies with time, as thermal fluctuations can be observed if the light is analyzed at sufficiently high time resolution. Quantum mechanics interprets measurements of light intensity as photon counting, where the natural assumption is to use the Poisson distribution. When light intensity is integrated over large times longer than the coherence time, the Poisson-to-normal approximation is appropriate.

Measurement errors

Normality is the central assumption of the mathematical theory of errors. Similarly, in statistical model-fitting, an indicator of goodness of fit is that the residuals (as the errors are called in that setting) be independent and normally distributed. The assumption is that any deviation from normality needs to be explained. In that sense, both in model-fitting and in the theory of errors, normality is the only observation that need not be explained, being expected. However, if the original data are not normally distributed (for instance if they follow a Cauchy distribution), then the residuals will also not be normally distributed. This fact is usually ignored in practice.

Repeated measurements of the same quantity are expected to yield results which are clustered around a particular value. If all major sources of errors have been taken into account, it is assumed that the remaining error must be the result of a large number of very small additive effects, and hence normal. Deviations from normality are interpreted as indications of systematic errors which have not been taken into account. Whether this assumption is valid is debatable.

A famous and oft-quoted remark attributed to Gabriel Lippmann says: "Everyone believes in the [normal] law of errors: the mathematicians, because they think it is an experimental fact; and the experimenters, because they suppose it is a theorem of mathematics."

Physical characteristics of biological specimens

The sizes of full-grown animals is approximately lognormal. The evidence and an explanation based on models of growth was first published in the 1932 book Problems of Relative Growth by Julian Huxley.

Differences in size due to sexual dimorphism, or other polymorphisms like the worker/soldier/queen division in social insects, further make the distribution of sizes deviate from lognormality.

The assumption that linear size of biological specimens is normal (rather than lognormal) leads to a non-normal distribution of weight (since weight or volume is roughly proportional to the 2nd or 3rd power of length, and Gaussian distributions are only preserved by linear transformations), and conversely assuming that weight is normal leads to non-normal lengths. This is a problem, because there is no a priori reason why one of length, or body mass, and not the other, should be normally distributed. Lognormal distributions, on the other hand, are preserved by powers so the "problem" goes away if lognormality is assumed.

On the other hand, there are some biological measures where normality is assumed, such as blood pressure of adult humans. This is supposed to be normally distributed, but only after separating males and females into different populations (each of which is normally distributed).

Financial variables

The normal model of asset price movements does not capture extreme movements such as stock market crashes.

Already in 1900 Louis Bachelier proposed representing price changes of stocks using the normal distribution. This approach has since been modified slightly. Because of the multiplicative nature of compounding of returns, financial indicators such as stock values and commodity prices exhibit "multiplicative behavior". As such, their periodic changes (e.g., yearly changes) are not normal, but rather lognormal - i.e. logarithmic returns as opposed to values are normally distributed. This is still the most commonly used hypothesis in finance, in particular in option pricing in the Black–Scholes model.

However, in reality financial variables exhibit heavy tails, and thus the assumption of normality understates the probability of extreme events such as stock market crashes. Corrections to this model have been suggested by mathematicians such as Benoît Mandelbrot, who observed that the changes in logarithm over short periods (such as a day) are approximated well by distributions that do not have a finite variance, and therefore the central limit theorem does not apply. Rather, the sum of many such changes gives log-Levy distributions.

Distribution in standardized testing and intelligence

In standardized testing, results can be scaled to have a normal distribution; for example, the SAT's traditional range of 200–800 is based on a normal distribution with a mean of 500 and a standard deviation of 100. As the entire population is known, this normalization can be done, and allows the use of the Z test in standardized testing.

Sometimes, the difficulty and number of questions on an IQ test is selected in order to yield normal distributed results. Or else, the raw test scores are converted to IQ values by fitting them to the normal distribution. In either case, it is the deliberate result of test construction or score interpretation that leads to IQ scores being normally distributed for the majority of the population. However, the question whether intelligence itself is normally distributed is more involved, because intelligence is a latent variable, therefore its distribution cannot be observed directly.

Diffusion equation

The probability density function of the normal distribution is closely related to the (homogeneous and isotropic) diffusion equation and therefore also to the heat equation. This partial differential equation describes the time evolution of a mass-density function under diffusion. In particular, the probability density function

$\phi _{0,t}(x)={\tfrac {1}{\sqrt {2\pi t\,}}}e^{-{\frac {x^{2}}{2t}}},$

for the normal distribution with expected value 0 and variance t satisfies the diffusion equation:

${\frac {\partial }{\partial t}}\phi _{0,t}(x)={\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\phi _{0,t}(x).$

If the mass-density at time t = 0 is given by a Dirac delta, which essentially means that all mass is initially concentrated in a single point, then the mass-density function at time t will have the form of the normal probability density function with variance linearly growing with t. This connection is no coincidence: diffusion is due to Brownian motion which is mathematically described by a Wiener process, and such a process at time t will also result in a normal distribution with variance linearly growing with t.

More generally, if the initial mass-density is given by a function ϕ(x), then the mass-density at time t will be given by the convolution of ϕ and a normal probability density function.

Use in computational statistics

The normal distribution arises in many areas of statistics. For example, for a random variable with finite variance, the sampling distribution of the sample mean is approximately normal, even if the distribution of the population from which the sample is taken is not normal. However, for distributions with infinite or undefined variance, such as the Cauchy distribution, the sampling distribution of the sample mean need not be approximately normal.

In addition, the normal distribution maximizes information entropy among all distributions with known mean and variance, which makes it the natural choice of underlying distribution for data summarized in terms of sample mean and variance. The normal distribution is the most widely used family of distributions in statistics and many statistical tests are based on the assumption of normality.

Generating values for normal random variables

For computer simulations, it is often useful to generate values that have a normal distribution. There are several methods and the most basic is to invert the standard normal cdf. More efficient methods are also known, one such method being the Box–Muller transform. An even faster algorithm is the ziggurat algorithm. These are discussed below. A simple approach that is easy to program is as follows. Simply sum 12 uniform (0, 1) deviates and subtract 6 (half of 12). This is quite usable in many applications. The sum over these 12 values has an Irwin–Hall distribution; 12 is chosen to give the sum a variance of exactly one. The resulting random deviates are limited to the range (−6, 6) and have a density which is a 12-section eleventh-order polynomial approximation to the normal distribution.

The Box–Muller method says that, if you have two independent random numbers U and V uniformly distributed on (0, 1], (e.g. the output from a random number generator), then two independent standard normally distributed random variables are X and Y, where:

$X={\sqrt {-2\ln U}}\,\cos(2\pi V),$

$Y={\sqrt {-2\ln U}}\,\sin(2\pi V).$

This formulation arises because the chi-square distribution with two degrees of freedom (see property 4 above) is an easily-generated exponential random variable (which corresponds to the quantity ln U in these equations). Thus an angle is chosen uniformly around the circle via the random variable V, a radius is chosen to be exponential and then transformed to (normally distributed) x and y coordinates.

George Marsaglia developed the Ziggurat algorithm, which is faster than the Box–Muller transform and still exact. In about 97% of all cases it uses only two random numbers, one random integer and one random uniform, one multiplication and an if-test. Only in 3% of the cases where the combination of those two falls outside the "core of the ziggurat" a kind of rejection sampling using logarithms, exponentials and more uniform random numbers has to be employed.

There is also some investigation into the connection between the fast Hadamard transform and the normal distribution, since the transform employs just addition and subtraction and by the central limit theorem random numbers from almost any distribution will be transformed into the normal distribution. In this regard a series of Hadamard transforms can be combined with random permutations to turn arbitrary data sets into a normally-distributed data.

Numerical approximations of the normal distribution and its cdf

The normal distribution function is widely used in scientific and statistical computing. Therefore, it has been implemented in various ways.

The GNU Scientific Library calculates values of the standard normal cdf using piecewise approximations by rational functions. Another approximation method uses third-degree polynomials on intervals. The article on the bc programming language gives an example of how to compute the cdf in Gnu bc with George Marsaglia algorithm.

For a more detailed discussion of how to calculate the normal distribution, see Knuth's The Art of Computer Programming, section 3.4.1C.

An algorithm made by Graem West, based on Hart's algorithm 5666 (1968), provides quicker result than the one found by George Marsaglia with same level of accuracy.

See also

Template:Statistics portal Related distributions

• Multivariate normal distribution — normally distributed vectors
• Complex normal distribution — complex normal random variables and vectors
• Matrix normal distribution — normally distributed matrices
• Gaussian process — normal stochastic processes
  • Wiener process
  • Brownian bridge
  • Ornstein-Uhlenbeck process
• Pearson distribution — generalized family of probability distributions that extend the Gaussian distribution to include different skewness and kurtosis values

others

• Behrens–Fisher problem
• Bell curve grading
• Central limit theorem - average of a sufficiently large number of identically distributed independent random variables each with finite mean and variance will be approximately normally distributed
• Data transformation (statistics) - simple techniques to transform data into normal distribution
• Erdős-Kac theorem, on the occurrence of the normal distribution in number theory
• Gaussian blur, convolution using the normal distribution as a kernel
• Gaussian function
• Isserlis Gaussian moment theorem
• Normally distributed and uncorrelated does not imply independent (an example of two normally distributed uncorrelated random variables that are not independent; this cannot happen in the presence of joint normality)
• Probit function
• Sum of normally distributed random variables

References

• John Aldrich. Earliest Uses of Symbols in Probability and Statistics. Electronic document, retrieved March 20, 2005. (See "Symbols associated with the Normal Distribution".)
• Bernardo, J. M. (2000). Bayesian Theory. Wiley. ISBN 0-471-49464-X. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Abraham de Moivre (1738). The Doctrine of Chances.
• Stephen Jay Gould (1981). The Mismeasure of Man. First edition. W. W. Norton. ISBN 0-393-01489-4 .
• Havil, 2003. Gamma, Exploring Euler's Constant, Princeton, NJ: Princeton University Press, p. 157.
• R. J. Herrnstein and Charles Murray (1994). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 0-02-914673-9 .
• Pierre-Simon Laplace (1812). Analytical Theory of Probabilities.
• Jeff Miller, John Aldrich, et al. Earliest Known Uses of Some of the Words of Mathematics. In particular, the entries for "bell-shaped and bell curve", "normal" (distribution), "Gaussian", and "Error, law of error, theory of errors, etc.". Electronic documents, retrieved December 13, 2005.
• S. M. Stigler (1999). Statistics on the Table, chapter 22. Harvard University Press. (History of the term "normal distribution".)
• Eric W. Weisstein et al. Normal Distribution at MathWorld. Electronic document, retrieved March 20, 2005.
• Marvin Zelen and Norman C. Severo (1964). Probability Functions. Chapter 26 of Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed, by Milton Abramowitz and Irene A. Stegun. National Bureau of Standards.

External links

The normal distribution

• Mathworld: Normal Distribution
• PlanetMath: normal random variable
• Intuitive derivation.
• Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics
• Maxwell demons: Simulating probability distributions with functions of propositional calculus
• Visualization of normal distribution
• XLL Excel Addin function for Normal Dist. Random Number Generator

Online results and applications

• Normal distribution table
• Public Domain Normal Distribution Table
• Distribution Calculator – Calculates probabilities and critical values for normal, t, chi-square and F-distribution.
• Java Applet on Normal Distributions
• Free Area Under the Normal Curve Calculator from Daniel Soper's Free Statistics Calculators website.
• Interactive Graph of the Standard Normal Curve Quickly Visualize the one and two-tailed area of the Standard Normal Curve
• Javascript calculator which calculates the probability that a value randomly chosen from a Normal Distribution is greater than, less than or between chosen values
• Standard Normal Distribution Table for the iPhone

Algorithms and approximations

• GNU Scientific Library – Reference Manual – The Gaussian Distribution
• Calculating the Cumulative Normal distribution, C++, VBA, sitmo.com
• An algorithm for computing the inverse normal cumulative distribution function by Peter J. Acklam – has examples for several programming languages
• An Approximation to the Inverse Normal(0, 1) Distribution, gatech.edu
• Handbook of Mathematical Functions: Polynomial and Rational Approximations for P(x) and Z(x), Abramowitz and Stegun