Jump to content

Schulze method: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
No edit summary
Line 338: Line 338:
* [http://www.boardgamegeek.com/article/2582330 Golden Geek Awards 2008 - Nominations Open], August 2008
* [http://www.boardgamegeek.com/article/2582330 Golden Geek Awards 2008 - Nominations Open], August 2008
* [http://www.boardgamegeek.com/article/3840078 Golden Geek Awards 2009 - Nominations Open], August 2009
* [http://www.boardgamegeek.com/article/3840078 Golden Geek Awards 2009 - Nominations Open], August 2009
* [http://www.boardgamegeek.com/article/5492260 Golden Geek Awards 2010 - Nominations Open], September 2010</ref>
* [http://www.boardgamegeek.com/article/5492260 Golden Geek Awards 2010 - Nominations Open], September 2010
* [http://boardgamegeek.com/thread/694044 2011 Golden Geek Awards - Nominations open! For Board Games, RPGs and Video Games], September 2011</ref>
* [[Apache Cassandra|Cassandra]] <ref>[http://article.gmane.org/gmane.comp.db.cassandra.devel/424/match=condorcet+schwartz+sequential+dropping+beatpath Project Logo], October 2009</ref>
* [[Apache Cassandra|Cassandra]] <ref>[http://article.gmane.org/gmane.comp.db.cassandra.devel/424/match=condorcet+schwartz+sequential+dropping+beatpath Project Logo], October 2009</ref>
* [http://0xAA.org Codex Alpe Adria] <ref>{{cite web|url=http://0xAA.org/competitions/ |title=Codex Alpe Adria Competitions |publisher=0xaa.org |date=2010-01-24 |accessdate=2010-05-08}}</ref>
* [http://0xAA.org Codex Alpe Adria] <ref>{{cite web|url=http://0xAA.org/competitions/ |title=Codex Alpe Adria Competitions |publisher=0xaa.org |date=2010-01-24 |accessdate=2010-05-08}}</ref>

Revision as of 15:39, 22 September 2011

A joint Politics and Economics series
Social choice and electoral systems
Single-winner methods
Single vote - plurality methods

Condorcet methods

Positional voting

Cardinal voting

Proportional representation
Party-list

Quota-remainder methods

Approval-based committees

Fractional social choice

Semi-proportional representation

Mixed systems
By results of combination
By mechanism of combination

By ballot type

Paradoxes and pathologies
Spoiler effects

Pathological response

Strategic voting

Paradoxes of majority rule

Social and collective choice
Impossibility theorems

Positive results

icon Mathematics portal

The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential Dropping (SSD), Cloneproof Schwartz Sequential Dropping (CSSD), the Beatpath Method, Beatpath Winner, Path Voting, and Path Winner.

The Schulze method is a Condorcet method, which means the following: if there is a candidate who is preferred over every other candidate in pairwise comparisons, then this candidate will be the winner when the Schulze method is applied.

Currently, the Schulze method is the most widespread Condorcet method (list). The Schulze method is used by several organizations including Wikimedia, Debian, Gentoo, and Software in the Public Interest.

The output of the Schulze method (defined below) gives an ordering of candidates. Therefore, if several positions are available, the method can be used for this purpose without modification, by letting the k top-ranked candidates win the k available seats. Furthermore, for proportional representation elections, a single transferable vote variant has been proposed.

Description of the method

Ballot

The input to the Schulze method is the same as for other preferential single-winner election methods: each voter must furnish an ordered preference list on candidates where ties are allowed.

One typical way for voters to specify their preferences on a ballot (see left) is as follows. Each ballot lists all the candidates, and each voter ranks this list in order of preference using numbers: the voter places a '1' beside the most preferred candidate(s), a '2' beside the second-most preferred, and so forth. Each voter may optionally

  • give the same preference to more than one candidate. This indicates that this voter is indifferent between these candidates.
  • use non-consecutive numbers to express preferences. This has no impact on the result of the elections, since only the order in which the candidates are ranked by the voter matters, and not the absolute numbers of the preferences.
  • keep candidates unranked. When a voter doesn't rank all candidates, then this is interpreted as if this voter (i) strictly prefers all ranked to all unranked candidates, and (ii) is indifferent among all unranked candidates.

Schulze Method

Let d[V,W] be the number of voters who prefer candidate V to candidate W.

A path from candidate X to candidate Y of strength p is a sequence of candidates C(1),...,C(n) with the following properties:

  1. C(1) = X and C(n) = Y.
  2. For all i = 1,...,(n-1): d[C(i),C(i+1)] > d[C(i+1),C(i)].
  3. For all i = 1,...,(n-1): d[C(i),C(i+1)] ≥ p.

p[A,B], the strength of the strongest path from candidate A to candidate B, is the maximum value such that there is a path from candidate A to candidate B of that strength. If there is no path from candidate A to candidate B at all, then p[A,B] = 0.

Candidate D is better than candidate E if and only if p[D,E] > p[E,D].

Candidate D is a potential winner if and only if p[D,E] ≥ p[E,D] for every other candidate E.

It can be proven that p[X,Y] > p[Y,X] and p[Y,Z] > p[Z,Y] together imply p[X,Z] > p[Z,X].[1]: §4.1  Therefore, it is guaranteed (1) that the above definition of "better" really defines a transitive relation and (2) that there is always at least one candidate D with p[D,E] ≥ p[E,D] for every other candidate E.

Example

Consider the following example, in which 45 voters rank 5 candidates.

  • 5 ACBED (meaning, 5 voters have order of preference: A > C > B > E > D)
  • 5 ADECB
  • 8 BEDAC
  • 3 CABED
  • 7 CAEBD
  • 2 CBADE
  • 7 DCEBA
  • 8 EBADC

First, we compute the pairwise preferences. For example, in comparing A and B pairwise, there are 5+5+3+7=20 voters who prefer A to B, and 8+2+7+8=25 voters who prefer B to A. So d[A, B] = 20 and d[B, A] = 25. The full set of pairwise preferences is:

Directed graph labeled with pairwise preferences d[*, *]
Matrix of pairwise preferences
d[*,A] d[*,B] d[*,C] d[*,D] d[*,E]
d[A,*] 20 26 30 22
d[B,*] 25 16 33 18
d[C,*] 19 29 17 24
d[D,*] 15 12 28 14
d[E,*] 23 27 21 31

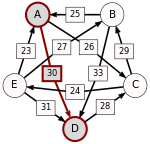
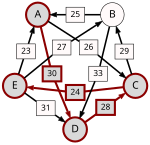
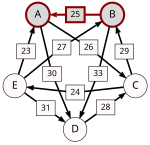
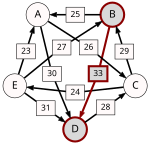
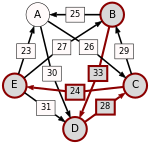
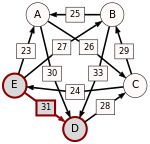
To help visualize the strongest paths, the diagram on the right-hand side shows an arrow from A to B with label d[A, B], in the style of a directed graph. (To avoid cluttering the diagram we only draw d[A, B] when d[A, B] represents a majority of voters, which turns out not to affect the result in this case.)

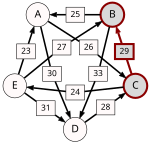
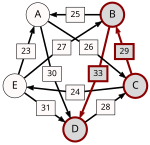
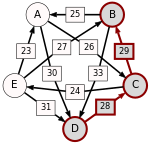
Recall that the strength of a path is the strength of its weakest link. One example of computing the strongest path strength is p[B, D] = 33: the strongest path from B to D is the direct path (B, D) which has strength 33. For contrast, let us also compute p[A, C]. The strongest path from A to C is not the direct path (A, C) of strength 26, rather the strongest path is the indirect path (A, D, C) which has strength min(30, 28) = 28.

For each pair of candidates X and Y, the following table shows the strongest path from candidate X to candidate Y in red, with the weakest link underlined.

Strongest paths
... to A ... to B ... to C ... to D ... to E
from A ...
A-(30)-D-(28)-C-(29)-B
A-(30)-D-(28)-C
A-(30)-D
A-(30)-D-(28)-C-(24)-E 		from A ...
from B ...
B-(25)-A
B-(33)-D-(28)-C
B-(33)-D
B-(33)-D-(28)-C-(24)-E 		from B ...
from C ...
C-(29)-B-(25)-A
C-(29)-B
C-(29)-B-(33)-D
C-(24)-E 		from C ...
from D ...
D-(28)-C-(29)-B-(25)-A
D-(28)-C-(29)-B
D-(28)-C
D-(28)-C-(24)-E 		from D ...
from E ...
E-(31)-D-(28)-C-(29)-B-(25)-A
E-(31)-D-(28)-C-(29)-B
E-(31)-D-(28)-C
E-(31)-D		 from E ...
... to A ... to B ... to C ... to D ... to E
Strengths of the strongest paths
p[*,A] p[*,B] p[*,C] p[*,D] p[*,E]
p[A,*] 28 28 30 24
p[B,*] 25 28 33 24
p[C,*] 25 29 29 24
p[D,*] 25 28 28 24
p[E,*] 25 28 28 31

Now we can determine the output of the Schulze method. Comparing A and B for example, since 28 = p[A,B] > p[B,A] = 25, for the Schulze method candidate A is better than candidate B. Another example is that 31 = p[E,D] > p[D,E] = 24, so candidate E is better than candidate D. Continuing in this way we get the Schulze ranking is E > A > C > B > D, and E wins. In other words, E wins since p[E,X] ≥ p[X,E] for every other candidate X.

Implementation

The only difficult step in implementing the Schulze method is computing the strongest path strengths. However, this is a well-known problem in graph theory sometimes called the widest path problem. One simple way to compute the strengths therefore is a variant of the Floyd–Warshall algorithm. The following pseudocode illustrates the algorithm. 

# Input: d[i,j], the number of voters who prefer candidate i to candidate j.
# Output: p[i,j], the strength of the strongest path from candidate i to candidate j.

for i from 1 to C
   for j from 1 to C
      if (i <> j) then
         if (d[i,j] > d[j,i]) then
            p[i,j] := d[i,j]
         else
            p[i,j] := 0

for i from 1 to C
   for j from 1 to C
      if (i <> j) then
         for k from 1 to C
            if (i <> k and j <> k) then
               p[j,k] := max ( p[j,k], min ( p[j,i], p[i,k] ) )

This algorithm is efficient, and has running time proportional to C3 where C is the number of candidates. (This does not account for the running time of computing the d[*,*] values, which if implemented in the most straightforward way, takes time proportional to C2 times the number of voters.)

Ties and alternative implementations

When we allow users to have ties in their preferences, the outcome of the Schulze method naturally depends on how we interpret these ties in defining d[*,*]. Two natural choices are that d[A, B] represents either the number of voters who strictly prefer A to B (A>B), or the margin of (voters with A>B) minus (voters with B>A). But no matter how the ds are defined, the Schulze ranking has no cycles, and assuming the ds are unique it has no ties.[1]

Although ties in the Schulze ranking are unlikely,[2] they are possible. Schulze's original paper[1] proposed breaking ties in accordance with a voter selected at random, and iterating as needed.

An alternative, slower, way to describe the winner of the Schulze method is the following procedure:

  1. draw a complete directed graph with all candidates, and all possible edges between candidates
  2. iteratively [a] delete all candidates not in the Schwartz set (i.e. any candidate which cannot reach all others) and [b] delete the weakest link
  3. the winner is the last non-deleted candidate.

Satisfied and failed criteria

Satisfied criteria

The Schulze method satisfies the following criteria:

Failed criteria

Since the Schulze method satisfies the Condorcet criterion, it automatically fails the following criteria:

Likewise, since the Schulze method is not a dictatorship and agrees with unanimous votes, Arrow's Theorem implies it fails the criterion

Comparison table

The following table compares the Schulze method with other preferential single-winner election methods:

Monotonic Condorcet Majority Condorcet loser Majority loser Mutual majority Smith ISDA Clone independence Reversal symmetry Polynomial time Participation, Consistency
Schulze Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes No
Ranked pairs Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes No
Kemeny-Young Yes Yes Yes Yes Yes Yes Yes Yes No Yes No No
Nanson No Yes Yes Yes Yes Yes Yes No No Yes Yes No
Baldwin No Yes Yes Yes Yes Yes Yes No No No Yes No
Instant-runoff voting No No Yes Yes Yes Yes No No Yes No Yes No
Borda Yes No No Yes Yes No No No No Yes Yes Yes
Bucklin Yes No Yes No Yes Yes No No No No Yes No
Coombs No No Yes Yes Yes Yes No No No No Yes No
MiniMax Yes Yes Yes No No No No No No No Yes No
Plurality Yes No Yes No No No No No No No Yes Yes
Anti-plurality Yes No No No Yes No No No No No Yes Yes
Contingent voting No No Yes Yes Yes No No No No No Yes No
Sri Lankan contingent voting No No Yes No No No No No No No Yes No
Supplementary voting No No Yes No No No No No No No Yes No
Dodgson No Yes Yes No No No No No No No No No

The main difference between the Schulze method and the ranked pairs method (both of which have tick the same boxes in the above table) can be seen in this example:

Suppose the MinMax score of a set X of candidates is the strength of the strongest pairwise win of a candidate A ∉ X against a candidate B ∈ X. Then the Schulze method, but not the ranked pairs method, guarantees that the winner is always a candidate of the set with minimum MinMax score.[1]: §4.8  So, in some sense, the Schulze method minimizes the strongest pairwise win that has to be overturned when determining the winner.

History of the Schulze method

The Schulze method was developed by Markus Schulze in 1997. It was first discussed in public mailing lists in 1997–1998[4] and in 2000.[5] Subsequently, Schulze method users included Software in the Public Interest (2003),[6] Debian (2003),[7] Gentoo (2005),[8] TopCoder (2005),[9] Wikimedia (2008),[10] KDE (2008),[11] the Free Software Foundation Europe (2008),[12] the Pirate Party of Sweden (2009),[13] and the Pirate Party of Germany (2010).[14] In the French Wikipedia, the Schulze method was one of two multi-candidate methods approved by a majority in 2005,[15] and it has been used several times.[16]

In 2011, Schulze published the method in the academic journal Social Choice and Welfare.[1]

Use of the Schulze method

sample ballot for Wikimedia's Board of Trustees elections

The Schulze method is not currently used in parliamentary elections. However, it has been used for parliamentary primaries in the Swedish Pirate Party. It is also starting to receive support in other public organizations. Organizations which currently use the Schulze method are:

Notes

  1. ^ a b c d e f g h i j k l m n Markus Schulze, A new monotonic, clone-independent, reversal symmetric, and condorcet-consistent single-winner election method, Social Choice and Welfare, volume 36, number 2, page 267–303, 2011. Preliminary version in Voting Matters, 17:9-19, 2003.
  2. ^ Under reasonable probabilistic assumptions when the number of voters is much larger than the number of candidates
  3. ^ a b c Douglas R. Woodall, Properties of Preferential Election Rules, Voting Matters, issue 3, pages 8-15, December 1994
  4. ^ See:
  5. ^ See:
  6. ^ a b Process for adding new board members, January 2003
  7. ^ a b See:
  8. ^ a b See:
  9. ^ a b See:
  10. ^ a b See:
  11. ^ a b section 3.4.1 of the Rules of Procedures for Online Voting
  12. ^ a b See:
  13. ^ a b See:
  14. ^ a b 11 of the 16 regional sections and the federal section of the Pirate Party of Germany are using LiquidFeedback for unbinding internal opinion polls. In 2010/2011, the Pirate Parties of Neukölln (link), Mitte (link), Steglitz-Zehlendorf (link), Lichtenberg (link), and Tempelhof-Schöneberg (link) adopted the Schulze method for its primaries. In 2011, the Pirate Party of Berlin adopted this method for its primaries (link).
  15. ^ a b Choix dans les votes
  16. ^ fr:Spécial:Pages liées/Méthode Schulze
  17. ^ Election of the Annodex Association committee for 2007, February 2007
  18. ^ Condorcet method for admin voting, January 2005
  19. ^ See:
  20. ^ Project Logo, October 2009
  21. ^ "Codex Alpe Adria Competitions". 0xaa.org. 2010-01-24. Retrieved 2010-05-08.
  22. ^ "Fellowship Guidelines" (PDF). Retrieved 2011-06-01.
  23. ^ Report on HackSoc Elections, December 2008
  24. ^ Adam Helman, Family Affair Voting Scheme - Schulze Method
  25. ^ appendix 1 of the constitution
  26. ^ Logo Competition, May 2009
  27. ^ See:
  28. ^ "Guidance Document". Eudec.org. 2009-11-15. Retrieved 2010-05-08.
  29. ^ article XI section 2 of the bylaws
  30. ^ Democratic election of the server admins, July 2010
  31. ^ article 51 of the statutory rules
  32. ^ Free Geek Needs You!, September 2011
  33. ^ See:
  34. ^ GnuPG Logo Vote, November 2006
  35. ^ §14 of the bylaws
  36. ^ "User Voting Instructions". Gso.cs.binghamton.edu. Retrieved 2010-05-08.
  37. ^ Haskell Logo Competition, March 2009
  38. ^ A club by any other name ..., April 2009
  39. ^ See:
  40. ^ Knight Foundation awards $5000 to best created-on-the-spot projects, June 2009
  41. ^ See:
  42. ^ article 8.3 of the bylaws
  43. ^ See:
  44. ^ Lumiera Logo Contest, January 2009
  45. ^ The MKM-IG uses Condorcet with dual dropping. That means: The Schulze ranking and the ranked pairs ranking are calculated and the winner is the top-ranked candidate of that of these two rankings that has the better Kemeny score. See:
  46. ^ "Wahlmodus" (in Template:De icon). Metalab.at. Retrieved 2010-05-08.{{cite web}}: CS1 maint: unrecognized language (link)
  47. ^ Benjamin Mako Hill, Voting Machinery for the Masses, July 2008
  48. ^ See:
  49. ^ See:
  50. ^ 2009 Director Elections
  51. ^ NSC Jersey election, NSC Jersey vote, September 2007
  52. ^ Online Voting Policy
  53. ^ 2010 OpenStack Community Election, November 2010
  54. ^ "Voting Procedures". Parkscholars.org. Retrieved 2010-05-08.
  55. ^ §6(10) of the bylaws
  56. ^ 23 January 2011 meeting minutes
  57. ^ Piratenversammlung der Piratenpartei Schweiz, September 2010
  58. ^ 2006 Community for Pittsburgh Ultimate Board Election, September 2006
  59. ^ LogoVoting, December 2007
  60. ^ See:
  61. ^ Squeak Oversight Board Election 2010, March 2010
  62. ^ See:
  63. ^ Election status update, September 2009
  64. ^ Minutes of the 2010 Annual Sverok Meeting, November 2010
  65. ^ See this mail.
  66. ^ See:
  67. ^ See e.g. here (May 2009), here (August 2009), and here (December 2009).
  68. ^ See here and here.
  69. ^ See:
Wikimedia Commons has media related to Schulze method.

General

Tutorials

Advocacy

Books

Software

Legislative projects

Template:Link GA

Retrieved from "https://en.wikipedia.org/w/index.php?title=Schulze_method&oldid=451863708"