Regular tetrahedron

A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. It is one of the five regular Platonic solids, which have been known since antiquity.

In a regular tetrahedron, all faces are the same size and shape (congruent) and all edges are the same length.

Five tetrahedra are laid flat on a plane, with the highest 3-dimensional points marked as 1, 2, 3, 4, and 5. These points are then attached to each other and a thin volume of empty space is left, where the five edge angles do not quite meet.

Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they form the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are not regular, including the Schläfli orthoscheme and the Hill tetrahedron, can tessellate.

The regular tetrahedron is self-dual, which means that its dual is another regular tetrahedron. The compound figure comprising two such dual tetrahedra form a stellated octahedron or stella octangula.

Coordinates for a regular tetrahedron

The following Cartesian coordinates define the four vertices of a tetrahedron with edge length 2, centered at the origin, and two level edges:

$\left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)$

Expressed symmetrically as 4 points on the unit sphere, centroid at the origin, with lower face level, the vertices are:

$v_{1}=\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right)$

$v_{2}=\left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right)$

$v_{3}=\left(-{\sqrt {\frac {2}{9}}},-{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right)$

$v_{4}=(0,0,1)$

with the edge length of ${\sqrt {\frac {8}{3}}}$.

Still another set of coordinates are based on an alternated cube or demicube with edge length 2. This form has Coxeter diagram and Schläfli symbol h{4,3}. The tetrahedron in this case has edge length 2√2. Inverting these coordinates generates the dual tetrahedron, and the pair together form the stellated octahedron, whose vertices are those of the original cube.

Tetrahedron: (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)

Dual tetrahedron: (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)

Regular tetrahedron ABCD and its circumscribed sphere

Angles and distances

For a regular tetrahedron of edge length a:

Face area	$A_{0}={\frac {\sqrt {3}}{4}}a^{2}\,$
Surface area	$A=4\,A_{0}={\sqrt {3}}a^{2}\,$
Height of pyramid	$h={\frac {\sqrt {6}}{3}}a={\sqrt {\frac {2}{3}}}\,a\,$
Centroid to vertex distance	${\frac {3}{4}}\,h={\frac {\sqrt {6}}{4}}\,a={\sqrt {\frac {3}{8}}}\,a\,$
Edge to opposite edge distance	$l={\frac {1}{\sqrt {2}}}\,a\,$
Volume	$V={\frac {1}{3}}A_{0}h={\frac {\sqrt {2}}{12}}a^{3}={\frac {a^{3}}{6{\sqrt {2}}}}\,$
Face-vertex-edge angle	$\arccos \left({\frac {1}{\sqrt {3}}}\right)=\arctan \left({\sqrt {2}}\right)\,$ (approx. 54.7356°)
Face-edge-face angle, i.e., "dihedral angle"	$\arccos \left({\frac {1}{3}}\right)=\arctan \left(2{\sqrt {2}}\right)\,$ (approx. 70.5288°)
Vertex-Center-Vertex angle, the angle between lines from the tetrahedron center to any two vertices. It is also the angle between Plateau borders at a vertex. In chemistry it is called the tetrahedral bond angle. This angle (in radians) is also the arclength of the geodesic segment on the unit sphere resulting from centrally projecting one edge of the tetrahedron to the sphere.	$\arccos \left(-{\frac {1}{3}}\right)=2\arctan \left({\sqrt {2}}\right)\,$ (approx. 109.4712°)
Solid angle at a vertex subtended by a face	$\arccos \left({\frac {23}{27}}\right)$ (approx. 0.55129 steradians) (approx. 1809.8 square degrees)
Radius of circumsphere	$R={\frac {\sqrt {6}}{4}}a={\sqrt {\frac {3}{8}}}\,a\,$
Radius of insphere that is tangent to faces	$r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}}\,$
Radius of midsphere that is tangent to edges	$r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}}\,$
Radius of exspheres	$r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}\,$
Distance to exsphere center from the opposite vertex	$d_{\mathrm {VE} }={\frac {\sqrt {6}}{2}}a={\sqrt {\frac {3}{2}}}a\,$

With respect to the base plane the slope of a face (2√2) is twice that of an edge (√2), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).

For a regular tetrahedron with side length a, radius R of its circumscribing sphere, and distances d_i from an arbitrary point in 3-space to its four vertices, we have

${\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2};\\4\left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}$

Isometries of the regular tetrahedron

The proper rotations, (order-3 rotation on a vertex and face, and order-2 on two edges) and reflection plane (through two faces and one edge) in the symmetry group of the regular tetrahedron

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other.

The tetrahedron is the only Platonic solid that is not mapped to itself by point inversion.

The regular tetrahedron has 24 isometries, forming the symmetry group T_d, [3,3], (*332), isomorphic to the symmetric group, S₄. They can be categorized as follows:

• T, [3,3]⁺, (332) is isomorphic to alternating group, A₄ (the identity and 11 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation):
  • identity (identity; 1)
  • rotation about an axis through a vertex, perpendicular to the opposite plane, by an angle of ±120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; ⁠1 ± i ± j ± k/2⁠)
  • rotation by an angle of 180° such that an edge maps to the opposite edge: 3 ((1 2)(3 4), etc.; i, j, k)
• reflections in a plane perpendicular to an edge: 6
• reflections in a plane combined with 90° rotation about an axis perpendicular to the plane: 3 axes, 2 per axis, together 6; equivalently, they are 90° rotations combined with inversion (x is mapped to −x): the rotations correspond to those of the cube about face-to-face axes

Orthogonal projections of the regular tetrahedron

The regular tetrahedron has two special orthogonal projections, one centered on a vertex or equivalently on a face, and one centered on an edge. The first corresponds to the A₂ Coxeter plane.

Orthographic projection

Centered by	Face/vertex	Edge
Image
Projective symmetry	[3]	[4]

Cross section of regular tetrahedron

A central cross section of a regular tetrahedron is a square.

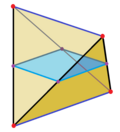
The two skew perpendicular opposite edges of a regular tetrahedron define a set of parallel planes. When one of these planes intersects the tetrahedron the resulting cross section is a rectangle. When the intersecting plane is near one of the edges the rectangle is long and skinny. When halfway between the two edges the intersection is a square. The aspect ratio of the rectangle reverses as you pass this halfway point. For the midpoint square intersection the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.

A tetragonal disphenoid viewed orthogonally to the two green edges.

This property also applies for tetragonal disphenoids when applied to the two special edge pairs.

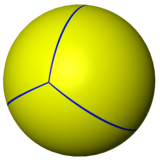
Spherical tiling

The tetrahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Orthographic projection	Stereographic projection

Helical stacking

A single 30-tetrahedron ring Boerdijk–Coxeter helix within the 600-cell, seen in stereographic projection

Regular tetrahedra can be stacked face-to-face in a chiral aperiodic chain called the Boerdijk–Coxeter helix. In four dimensions, all the convex regular 4-polytopes with tetrahedral cells (the 5-cell, 16-cell and 600-cell) can be constructed as tilings of the 3-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope's boundary surface.