Talk:Centrifugal force (rotating reference frame)

The centrifuge

Does the centrifugal force that causes stuff to move to the outer edge of a centrifuge come under the real or fictitious category? If it is real, it is certainly not a reactive force. If it is fictitious, it has got a very real effect.

I suggest that the introduction be tidied up such as to define centrifugal force without splitting it into a real kind and a fictitious kind. 203.115.188.254 (talk) 11:01, 4 April 2008 (UTC)

There happen to be two competing (and incompatible) uses of the term, and lack of perception of the differences continues to cause many confusions and even disputes in academia. Thus, how do you propose to do such "cleaning up" without recreating the kind of confusion that this article gets rid of from the start?

About your example: There is no real direct force that causes stuff to move to the outer edge; such a hypothetical force can have no real effect. However, moving objects resist changing their trajectory, and that causes a very real reactive force against the centrifuge wall. Do you think that it may be useful to add this example? Harald88 (talk) 16:19, 6 April 2008 (UTC)

Harald88, In planetary orbital theory, an elliptical orbit is the result of an inward radial force of gravity and a very real outward radial force which is the centrifugal force.

In the centrifuge, gravity is neglible and so we only have the centrifugal force.

The orbital solution to a centrifugal force acting in isolation without gravity is an infinitely eccentric hyperbola. This translates into a straight line in the laboratory.

In the centrifuge, a very real effect occurs, but you say that this is simply due to the tendency of moving objects to resist changing their trajectory. This tendency is known as inertia and it is equivalent to centrifugal force in the laboratory. It is a very real effect.

Hence, I do not accept that centrifugal force is a fictitious effect. If it can bring about a real effect in a centrifuge, then it is real. David Tombe (talk) 07:29, 16 April 2008 (UTC)

You did not answer my question. Do you think that it may be useful to add this example? Harald88 (talk) 09:21, 20 April 2008 (UTC)

Harald88, By all means put in a section about the centrifuge. It totally undermines the existing introduction which tries to claim that centrifugal force applies to two different things, one real and one fictitious, which just happen to act in the same place at the same time.

In the centrifuge, would they try to argue that the centrifugal force only becomes real at the moment when the heavy particles hit the edge?

That would be the same as saying that gravity for a man falling over a cliff only becomes real when he hits the ground. David Tombe (talk) 13:28, 21 April 2008 (UTC)

Is it real or fictitious?

The main article seems to be hedging its bets. It claims that there are two kinds of centrifugal force, with one kind being real and the other kind being fictitious. It then gives examples of each kind but goes on to admit that both of these kinds are the same thing.

The problem seems to be that modern literature presents centrifugal force to be a fictitious force, whereas classical literature presents it as a real force.

Even in the absence of a resolution of this controversy, the main article needs to be tidied up. We need to explain what centrifugal force is, without mentioning whether it is real or fictitious.

There then needs to be sections giving reasons for suggesting that it is fictitious, and sections giving reasons for suggesting that it is real.

But in its current form, the article is unsatisfactory because it talks of two kinds of centrifugal force when in fact there is only one kind. David Tombe (talk) 05:45, 18 April 2008 (UTC)

No, the two uses are entirely incompatible, and I thought that the article makes that clear - one of the purposes of this article is to end such confusion and misjudgment. Where did you get that idea, which sentence needs to be improved?

Note also that the article refers to a modern encyclopdia (edition of 2007) that defines centrifugal force as a reaction force.

Thanks, Harald88 (talk) 09:19, 20 April 2008 (UTC)

Harald88, the example of the swerving car in the so-called consensus version totally undermines what you have just said. It is trying to make out that the fictitious centrifugal force and the real centrifugal force are the same thing depending on how you view it.

The version which I put in, which you didn't see because it was changed by Thermochap, merely states the facts as regards what centrifugal force is. It then points out that it used to be regarded as real, but that it is now regarded as fictitious. If you say that a 2007 encyclopaedia states that it is real, then that is a clear sign that there is no consensus on the matter within the physics community. David Tombe (talk) 12:31, 20 April 2008 (UTC)

The Introduction

Thermochap, I thought that the middle paragraph of your new introduction was unnecessarily complicated. It involved the Affine connection. Overall, I'm not happy with it because you have acknowledged that centrifugal force is a real reaction to a centripetal force and then brushed that fact under the carpet as being history. What do you call that real reaction effect now if it is no longer considered to be centrifugal force?

Meanwhile, you have emphasized the modern view that centrifugal force is only a fictitious effect as viewed from a rotating frame of reference, when in fact you are perfectly aware yourself that the effect is real.

I had deliberately worded the article in such as way as to point out that nowadays, centrifugal force is considered to be fictitious, whereas in days of old, it was considered to be real.David Tombe (talk) 08:14, 20 April 2008 (UTC)

David, we have been through all this long ago. It is clear to everybody that you don't understand the first thing about this article's subject. Please do not try to edit it, your attempts to do so invariably make the article wrong and completely out of tune with established physical understanding. I have reverted it. –Henning Makholm 08:19, 20 April 2008 (UTC)

Indeed, the use of the term as reaction force is less common nowadays, but that "old" meaning is related to Newtonian mechanics which led to the derivation of centripetal acceleration; which in turn is necessary for understanding the fictitious use of the term. Thus, although at a time I went along with putting the fictitious meaning first because of its greater popularity, for a logical and comprehensible explanation to the reader it is certainly better as it is now.

In spite of that, as long as people like David turn up, it appears that it is still not well enough explained - or perhaps the topic is just to difficult? I'm not sure. David, what should be changed so that you won't find it confusing anymore?

Thanks, Harald88 (talk) 09:14, 20 April 2008 (UTC)

I actually think that the introduction is better off without any reference to the archaic use of the term "centrifucal force" to denote the reaction force to a centripetal force. That could still be in the article, but somewhere nearer the end. I also think that it needs to be made clear early in the article that the term "fictitious force" has a very specific meaning. It is not the same as "fictional". It is not the opposite of "real". It is a force that enters the calculations when a non-inertial reference frame is used. --PeR (talk) 17:28, 20 April 2008 (UTC)

I agree with these points, mostly. However, we should be careful not to move the reaction force so far down that it appears to be merely a historical curiosity that can safely be skipped. That's what it is, of course, to one who groks the fictitious force, but it seems to me that regrettably often people confuse the two forces. Therefore readers deserves to have the difference between them explained in some detail. And it is far nicer to do that by saying, "here is an older meaning of the word, but beware that it is different from the mainstream meaning in such-and-such way", than to have to say "here is a stupid misconception that you must disabuse yourself of". Of course we can only do this because we have sources to show that the achaic sense of the term is not complete fuction -- but given that we do have those, grabbing the chance sounds like a good idea. –Henning Makholm 22:25, 20 April 2008 (UTC)

Actually, because the reaction force is precisely a historical curiosity that can safely be skipped, I think it does more harm than good to give it a prominent position. Lots of people just read the first paragraph, and they should get as good info as possible. We should keep the text as clear as possible, and keep distractions to a minimum. --PeR (talk) 20:49, 21 April 2008 (UTC)

The Consensus Version

Henning, In the so-called consensus version, you talk about two kinds of centrifugal force. You talk about a real kind, and then you talk about a fictitious kind.

Below that, you then describe a scenario in which centrifugal force is either real or fictitious according to how you look at it.

This is entirely unsatisfactory.

The version which you reverted was not mine. In the version which I put in yesterday, I merely described centrifugal force and then pointed out the fact that it used to be considered to be real, but that nowadays it is considered to be fictitious.David Tombe (talk) 12:35, 20 April 2008 (UTC)

No. The consensus version describes that the term "centrifugal force" has two different possible meanings, and then goes on to describe a situation that happen to illustrate both meanings. But even in the described situation the two meanings of "centrifugal force" refers to two different forces. –Henning Makholm 22:11, 20 April 2008 (UTC)

David, The centrifugal force was never considered to be real by Newton, Maxwell, or Bernoulli. If you want to put a statement like that you need to cite a source. Specifically you need to cite a source that says "the centrifugal force was considered to be real", or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 17:16, 20 April 2008 (UTC)

Thermochap pointed out this nice animation from commons:

Map and spin frame perspectives of forces associated with an object released after being spun around on a massless rope.

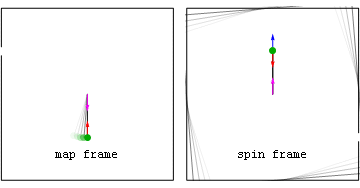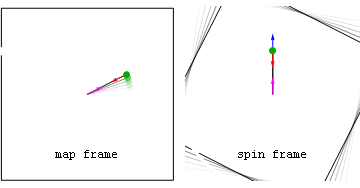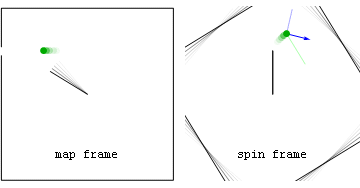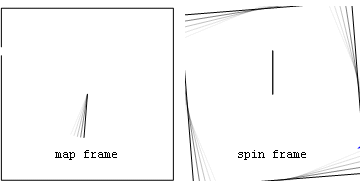
which nicely shows the difference between the two meanings described in the article. The red arrow is the centripetal force; the magenta one is the reactive centrifugal force, and the blue one is the fictitious force. I think this would make a good illustration for this article, if only the blue arrow had been decomposed into centrifugal and Coriolis terms after the green ball is let go. Names, aside, the force shown in magenta is and always was considered to be real; that shown in blue is and always was considered to be fictitious. –Henning Makholm 22:45, 20 April 2008 (UTC)

Henning, centrifugal force has only one meaning. The controversy lies in whether or not it is real or fictitious. The official position today is that it is fictitious. However, in former times, it was considered to be real.

I don't quite follow PeR's logic that if I were to provide a quote from an old paper confirming that centrifugal force was believed to be real, that this would have to be dismissed on the grounds that it was my original research.

The present introduction is totally unsatisfactory because it is trying to fudge the controversy by stating that the term centrifugal force has two different possible meanings.

The new introduction which I put in yesterday simply stated what centrifugal force is, and then further stated that the modern consensus is that centrifugal force is fictitious, whereas previously it had been regarded as real.David Tombe (talk) 07:11, 21 April 2008 (UTC)

If you don't understand what I said, then read WP:OR. Then read what I said again. I'm tired of repeating myself. --PeR (talk) 07:57, 21 April 2008 (UTC)

Admissibility of Evidence

PeR, I think that you are going to have to repeat yourself. We need to get something straight here regarding the issue of admissibility of evidence. You declared that centrifugal force was never considered to be real. You further went on to state that if I were to produce any quotes from Newton or Bernoulli which indicated that they believed that centrifugal force was real, that this would not be deemed to be admissible evidence on the grounds that it would be my own original research.

Here is a quote from Bernoulli out of the ET Whittaker book on the history of aethers.

"The elasticity which the Aether appears to possess, and in virtue of which it is able to transmit vibrations, is really due to the presence of these whirlpools; for, owing to centrifugal force, each whirlpool is continually striving to dilate, and so presses against the neighbouring whirlpools."

And here is a quote from Maxwell's paper 'On Physical Lines of Force',

"The explanation which most readily occurs to the mind is that the excess of pressure in the equatorial direction arises from the centrifugal force of vortices or eddies in the medium having their axes in directions parallel to the lines of force"

And you are trying to tell me that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real?

YES! I am trying to tell you that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real. However, if you don't want to accept this you don't have to. Just don't write anything in the article. If you do want to write something like that then you must (and here I am repeating myself, as requested) cite a source that says "the centrifugal force was considered to be real" or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 19:42, 21 April 2008 (UTC)

PeR, There is a controversy about whether or not centrifugal force is real. The official position today is that it is not real.

The current introduction is abominable because it tries to fudge the issue by pretending that there are two centrifugal forces. One for the realists, and one for the fictitiousists. This is an extreme case of ecclecticism. The current introduction cannot remain because it is a total disgrace.David Tombe (talk) 08:02, 21 April 2008 (UTC)

You misinterpret what it says. However, the fact that you don't understand it is evidence that it is not clearly enough written, so I agree that it should be rewritten. --PeR (talk) 19:42, 21 April 2008 (UTC)

Suggestions for improved and simplified introduction

PeR, I'm glad that you agree that the introduction should be re-written. So let's take it one step at a time.

First of all, I assume that we are both agreed that somewhere in the introduction there should be a statement clarifying that we should not be confusing centrifugal force with centripetal force.

And now, how about this for an introductory sentence?

"When an object is constrained to move in circular motion, an outward radial force will be observed to act on that object"

Would you agree that that is a correct statement of fact? There is certainly no need to distinguish between the reactive kind and the other kind because they are exactly the same effect.

Beyond that, I can't think that much more is needed in the introduction other than to state that a controversy exists regarding whether or not it is real or fictitious. David Tombe (talk) 02:13, 22 April 2008 (UTC)

Your proposal is not a correct statement of fact. It is simply false. An outward centrifugal force appears to act on an object only when it is described in a rotating coordinate system - and then not just for objects moving in circles, but for all object that are observed in that coordinate system. The outwards force that appears in an inertial system when an object moves in a circle does not act on the object that moves circularly, but on the constraints that make it move in a circle. This is clearly described in the article (at least when you have not recently vandalised it), and there are several descriptions of it to be found on this talk page.

Your continued assertions that these two forces are the same force are simply wrong. The two forces do not even apply to the same body. There is no controversy whatsoever about whether any of these forces are real or fictitious. Everybody agrees that the reactive force is (usually) real; and everybody agrees that the fictitious force is fictitious. Nothing of this will change because you continue to claim that it is false. –Henning Makholm 04:11, 22 April 2008 (UTC)

Henning, you are making it more complicated that it is. When an object is constrained to move in a circle, then an outward centrifugal force will act on it.

And there is a controversy about whether centrifugal force is real or fictitious. And there is only one centrifugal force. It is sheer double talk to split centrifugal force into two in order to cater for both beliefs. David Tombe (talk) 04:44, 22 April 2008 (UTC)

David, read what Henning wrote again. Your proposal is not a correct statement of fact. It is simply false. --PeR (talk) 07:04, 22 April 2008 (UTC)

PeR, OK, let's go through Henning Makholm's reply stage by stage. He says,

An outward centrifugal force appears to act on an object only when it is described in a rotating coordinate system

The very fact that we state the word 'outward' describes the effect perfectly without having to mention anything about rotating coordinate systems. Henning Makholm is making it more complicated than it is.

He then states,

- and then not just for objects moving in circles, but for all object that are observed in that coordinate system.

This statement was totally unnecessary because all objects that are observed in that coordinate system will be partaking in the circular motion in question. This was just a clouding statement.

Utter nonsense. Our choice to describe things from a rotating coordinate system cannot possibly make things move circularly. There is an infinitude of possible kinds of movements that are circular in neither an inertial coordinate system nor in a rotating one. –Henning Makholm 19:50, 22 April 2008 (UTC)

Henning, my apologies. I should have clarified that all objects that experience centrifugal force in that coordinate system will be partaking in the circular motion in question. We don't need to mention rotating frames. It is only necessary that an object be constrained to follow a curved path. David Tombe (talk) 05:38, 23 April 2008 (UTC)

He then states,

The outwards force that appears in an inertial system when an object moves in a circle does not act on the object that moves circularly, but on the constraints that make it move in a circle.

What happens in a centrifuge regarding the large particles before they reach the edge? Is the centrifugal force not acting on them?

When viewed from an inertial coordinate system, there is no centrifugal force acting on particles. Before they reach the edge, they drift with constant velocity within the centrifuge. When viewed from a co-rotating system, a centrifugal force acts on particles as they drift towards the edge, and keeps acting to pin them to the wall. In both cases the particles will start pushing the wall outwards once they stick to the wall (this is the reactive meaning of the centrifugal force). –Henning Makholm 19:50, 22 April 2008 (UTC)

Henning, Yes there is. These particles have been constrained to partake in the circular motion, and a centrifugal force acts radially outwards on them and causes them to accelerate towards the edge. If they were not constrained to move circularly with the centrifuge, then no centrifugal force would act on them. The centrifugal force is an absolute radial effect.David Tombe (talk) 06:03, 23 April 2008 (UTC)

He then says,

Your continued assertions that these two forces are the same force are simply wrong. The two forces do not even apply to the same body.

It's only in Henning Makholm's imagination that there are two centrifugal forces. No textbook ever states such a notion.

Perhaps not. But there are sufficient citations for either of the two different notions, and they are clearly two different notions, sharing essentially nothing but the name. –Henning Makholm 19:50, 22 April 2008 (UTC)

As for Henning Makholm's claim that the two forces don't even apply to the same body, he is only making the matter worse. In the example in the introduction to the main article, the bit that you call the fictitious centrifugal force acts to throw the man towards the car door. The bit which you call the reactive centrifugal force occurs by virtue of the man pushing against the car door as a result of that very same centrifugal force.

In this example, the fictitious centrifugal force applies to the passenger. The reactive centrifugal force applies to the car door. That is two different forces, and arguments about one causing the other does not make them into the same force. –Henning Makholm 19:50, 22 April 2008 (UTC)

Henning, it's a transmission of the same effect. It is splitting hairs to divide it into two different forces. That can all be discussed in the main article. There is no need to mention the reactive effect in the introduction.David Tombe (talk) 06:03, 23 April 2008 (UTC)

And he is saying that these two centrifugal forces do not act on the same body. It's like saying that the force with which a man hits the ground is not the same force as the gravity which caused him to fall over the cliff.

Of course they are not. The gravity applies to the man and causes him to accelerate downwards. Later, contact forces apply to the dirt where the man hits and cause the dirt to be rearranged. They are not the same force -- not only do they act on different bodies, they act at different times. Gravity acts continuously during the fall; the contact forces act only during the collision. –Henning Makholm 19:50, 22 April 2008 (UTC)

Henning, No. Even when the object is lying at rest on the Earth, gravity is still pushing it against the Earth. David Tombe (talk) 06:03, 23 April 2008 (UTC)

The man pushes against the car door because of the one and only centrifugal force.

From an inertial viewpoint, the man pushes against the car door because the car door pushes against the man, trying to make him turn a corner. In any case the reason why the man pushes is not the same as the force against the door that the pushing constitutes. –Henning Makholm 19:50, 22 April 2008 (UTC)

I need to have a citation which specifically states that centrifugal force applies to two different forces. David Tombe (talk) 08:04, 22 April 2008 (UTC)

I agree with your last statement. We need to cite a science-history book that states that Newton and others used the word "centrifugal force" with a different meaning than that which is used today. (The current references only show the usage of the term, which is not the same thing.) The rest of your analysis is just plain wrong. Sorry. My best advice is that you try reading the fictitious force article, some elementary mechanics textbooks, and then try reading Hennings text again. --PeR (talk) 10:00, 22 April 2008 (UTC)

What we seem to need is citations for the ordinary, fictitious, meaning of "centrifugal force". Once both meanings are properly cited to be (have been) in use, there will be no need to cite separately the obvious fact that the two meanings are different. –Henning Makholm 19:50, 22 April 2008 (UTC)~

Henning, That is not good enough. We know that there is centrifugal force. And we know that there are references that apply it to the reaction against the force that constrains the object to the curved path. But that is not sufficient to justify an unconventional claim that centrifugal force is a term which applies to two different forces. Such a claim is a grossly misleading exaggeration of the truth. David Tombe (talk) 06:03, 23 April 2008 (UTC)

PeR, so far your entire contribution to this debate has been to state that I am wrong and that I should read more of what Henning Makholm has to say, as if by reading his nonsense over and over again, then I might actually believe it eventually.

I'd like to hear your own analysis of the situation.

Let's go back to the very beginning. Tell me at what point this basic sentence goes wrong,

The centrifugal force is an outward radial force that acts on any object that is constrained to move in circular motion.David Tombe (talk) 13:32, 22 April 2008 (UTC)

Your statement doesn't properly describe the fictitious force (modern use of the term "centrifugal force"), because it fails to mention the rotating reference frame. It doesn't describe the reaction force (Newton's use of the term), because it says that it acts on the object itself, not the thing which is constraining it to move in a circle. --PeR (talk) 13:53, 22 April 2008 (UTC)

PeR, the fact that the object is constrained to move in circular motion caters for the rotating frame of reference aspect. As for the reaction bit, that can be dealt with in the main body of the article. That is an extension of the concept. A body which is being acted upon by a centrifugal force naturally transmits this force on when it comes into contact with another body. —Preceding unsigned comment added by David Tombe (talk • contribs) 14:38, 22 April 2008 (UTC)

This is utterly wrong. The choice of which reference frame to use (and hence whether or not one must consider a fictitious centrifugal force) can be made independently of how things move. Some choices may be more or less convenient according to whether they simply the movements, but the actual movements cannot make any choice of reference frame more or less correct. –Henning Makholm 19:50, 22 April 2008 (UTC)

The reasons for the reversion of the wikified version

The wikified version is teaching the false doctrine that centrifugal force is a term which applies to two different forces.

This doctrine is based on the idea that the centrifugal force which throws the passenger towards the door of the swerving car is a different force from the force which the passenger eventually causes on the door when contact is made.

The argument goes that a fictitious force throws the passenger to the car door and when contact is made, this is then transmitted into a real force which pushes against the door.

Such an argument is the same as saying that the force which an object causes on the Earth's surface due to its weight is a different force from the gravitional force that pushes the person against the surface of the Earth.

There is one force of gravity, and there is one centrifugal force.

The introduction to the article must describe in as simple terms as possible what that one centrifugal force is.David Tombe (talk) 13:47, 22 April 2008 (UTC)

I don't know whether what you say is true or not, but please IF you are going to rewrite the article, rewrite it in such a way that the article is wikified! Stephenb (Talk) 15:01, 22 April 2008 (UTC)

Looking at both versions of the text, I have to say it looks as though reverting was correct, but I'm no physicist. Have you guys thought of trying Wikipedia:Third opinion and getting another opinion? Stephenb (Talk) 15:29, 22 April 2008 (UTC)~

Stephen, thanks for replying. But I can assure you that the onus of wikification is on them. They need to provide a citation which clearly states that centrifugal force is a term which applies to two different forces. There is no textbook or encyclopaedia which will state that. David Tombe (talk) 05:41, 23 April 2008 (UTC)

You misunderstand. Wikification is the process of turning the text into an article, using proper grammar, formatting, references and citations. Whether or not your version or the other version contains faulty information is not why I reverted. The "consensus" version was wikified; yours was not, and looked like someone had edited it in bad faith resulting in a poor article, which is bordering on vandalism (since it appeared to remove information too). Stephenb (Talk) 09:10, 23 April 2008 (UTC)

In the old days, before about 1950, physics books called centrifugal force an inertial force. In those days inertial force was the term used for what today are labeled fictious forces. What this means is that the force is frame dependent. The force can be made to go away by simply switching from a noninertial frame to an inertial frame and the force disapears. The older terminology is certainly less of a problem, since students now wonder what is this fictious force? in my view the entire discussion of this is confusing and of questionable value as part of the article. There are no fictious forces, since they dont exist by definition of the word. So saying centrifugal force is fictious is the same as saying it doesnt exist. But since it does exist, that is bound to create confusion. I propose using the term frame dependent force since that captures the essential meaning of what is happening and we get rid of this textbook stupidity of fictious forces.Electrodynamicist (talk) 16:07, 22 April 2008 (UTC)

It is definitely worth mentioning that "fictitious force" is synonymous to the older "inertial force". Indeed it is a poorly chosen term, but this is an encyclopedia, not a place for redefining terminology. If it were, there certainly wouldn't be an article entitled imaginary number. --PeR (talk) 18:21, 22 April 2008 (UTC)

Update: Looking at some different uses of the term "inertial force" (including the Wikipedia disambig page inertial force) it seems the term has to meanings, in the same way as "centrifugal force" does. Thus, the sentence The centrifugal force is an inertial force. is correct in two ways (out of four :-). --PeR (talk) 09:50, 25 April 2008 (UTC)

Elliptical Motion

Henning, a rotating reference frame is irrelevant. The object in question has to actually be rotating with that reference frame before the centrifugal force will be induced. In other words, the object has to be constrained to move in circular motion.

There is no need to mention reference frames. In the swerving car scenario, the passenger is being constrained to follow the circular path by virtue of the back of his seat pushing him. A radially outward centrifugal force then occurs at right angles to this.

We must not lose track of the fact that this centrifugal effect is not something that is confined to circular motion. It occurs in any curved path motion. It occurs in elliptical and hyperbolic motion.

Therefore , mention of a rotating frame of reference merely confuses the issue because there could be an object which is stationary in the inertial frame. In the rotating frame, this object would trace out a circle, but it would experince no centrifugal force.

Regarding the 'reactive' centrifugal force, this is not a different force. It is an extension, or a transmission of the same effect. David Tombe (talk) 05:28, 23 April 2008 (UTC)

PeR

PeR, You have just reverted a perfectly good introduction to a shambles version. Did you even read what I said about elliptical motion? Anyway, a citation will be needed for the version which you have put in place.

We haven't even heard any evidence yet that you understand the issues in question. You seem to always just defer to what Henning Makholm says. The version which I put in was easier to read and it covered the key points. Nobody is disputing any fact which I wrote in that introduction. David Tombe (talk) 06:11, 23 April 2008 (UTC)

David, you might want to read through this. Notice how everybody else (including me) is politely trying to explain why you're wrong? Notice how nobody agrees with you? Maybe you should consider the possibility that the others may be right? --PeR (talk) 08:24, 23 April 2008 (UTC)

PeR, You obviously haven't been paying the slightest bit of attention to anything that has been going on. Your mind is totally locked into last year's argument.

We are not arguing about whether the centrifugal force is real or fictitious. That was last year's argument and I still have my own opinion on that matter.

At the moment, we are trying to clean up the existing introduction in certain key respects. These are notably,

(1) To avoid any specific statement, especially in the first line of the introduction, to the extent that centrifugal force is a term which is applied to two different forces.

The reality is that one of those effects is a transmitted effect of the other. That can be dealt with in the main body of the article. There is no need to deal with that in the introduction.

(ii) We need to generalize the wording to cater for all kinds of curved path motion. In the so-called consensus version, one might get the impression that centrifugal force only occurs with circular motion.

So far, your only contribution to this debate has been to continually repeat that I am wrong without even being specific as to which particular point you are talking about. And you seem to have a habbit of referring what other people have said.

Can we soon maybe hear some of your own views, just so that we can be sure that you actually understand the issues in question.David Tombe (talk) 08:52, 23 April 2008 (UTC)

The Recent Edits

Rracecarr, The edits that you undid were designed to generalize the situation to cater for curved motion generally, which it seems that you began to realize after you had made the reversion.

They were also designed to treat reactive centrifugal force as a knock effect rather than as a distinct force in its own right.

The version which you reverted to contains some errors. Notably it doesn't specify that an object has to be co-rotating in a rotating frame in order to experience centrifugal force.

Surely you must know that already. Centrifugal force is treated in modern applied maths courses as one of two inertial effects which supplement the true acceleration when we do a rotating coordinate frame transformation. In order for the centrifugal force to be non-zero the object must have a tangential speed of zero relative to the rotating frame.

Ideally, I would like to see the introduction very much simplified and all matters to do with reactive centrifugal force dealt with in a section in the main article.David Tombe (talk) 15:30, 23 April 2008 (UTC)

Errors in the intro

There are at least 2 errors in the version being pushed by DT. 1) Centrifugal force is present in a rotating frame whether or not the object rotates with the frame; 2) the centrifugal force does not act away from the focus--this is sloppy terminology. For example, the centripetal force experienced by a particle moving along a parabolic path does not in general point toward the focus of the parabola.Rracecarr (talk) 15:30, 23 April 2008 (UTC)

Rracecarr, Regarding point number (1), if an object is not co-rotating with a rotating frame, then it experiences no centrifugal force.

Imagine you are standing on the ground. Above you is a large rotating disc. Somebody sitting on that rotating disc will consider that you are tracing out a circular path. Neither he nor you will observe any centrifugal force.

You are getting confused with Coriolis force. Coriolis force is different because it is a tangential effect and a fictitious Coriolis effect can indeed be induced on an object which is moving, but not necessarily co-rotating with the frame. Centrifugal force is a radial force and it cannot be introduced as an artifact of rotation. But if somebody is constrained to co-rotate, then they will experience an outward radial centrifugal force.

On point number (2), yes it was sloppy terminology but I wanted to get the point started that we are not confined to circular motion.

What you should have done was improved the terminology. There was no need for a wholesale reversion. David Tombe (talk) 15:42, 23 April 2008 (UTC)

You are flat wrong that there is no centrifugal force if the object does not rotate with the frame. The centrifugal force in a rotating frame of reference is totally independent of the velocity of the object. It depends only on the position, and is only zero if the object is collocated with the axis of rotation. I'm not going to revert right now because I'm already past 3RR (as are you--I think you're at 5). Rracecarr (talk) 16:18, 23 April 2008 (UTC)

No Rracecarr, it is you that is totally wrong. If an object is not rotating with the frame, it will be tracing out a circle in that frame. There will be no centrifugal force acting on it in any shape or form.

To get centrifugal force, we need to have a tangential speed measured relative to the true inertial frame. Co-rotation with a rotating frame is a perfect scenario.

That might seem logical to do it that way. Unfortunately, that's not the way that the centrifugal force is defined. The centrifugal force is defined based solely on the rotation speed of the reference frame, and distance from the axis and the coriolis force compensates for any difference due to the motion of the particle. The advantage of this definition is that corotation isn't needed, and it can deal with particles moving in arbitrary ways, not just ones that happen to be rotating about a center.- (User) WolfKeeper (Talk) 16:29, 3 May 2008 (UTC)

When the car swerves around the corner, the seat of the car is constraining the passenger to co-rotate in the circle we the car is following. Hence a radial centrifugal force is induced which throws the passenger to the side door.

I can see that your confusion comes due to your special interest in Coriolis force. Fictitious Coriolis force has got important differences to centrifugal force.

Circular motion can induce tangential motion as an artifact. But it cannot induce radial motion as an artifact. Coriolis force is a tangential effect and centrifugal force is a radial effect.

In classical mecahnics, I'm sure you have done the equations. We end up with the two 'inertial terms'. One is Coriolis force. If we do a radial motion in the rotating frame, we will get an apparent tangential deflection as viewed from the rotating frame.

However, the centrifugal force term only becomes active if there is a tangential velocity as measured relative to the true frame. David Tombe (talk) 16:32, 23 April 2008 (UTC)

This edit misses the point. Centrifugal force is a useful concept in rotating reference frames, and it acts on all objects, whether they're moving in a curved path, a straight path, or not moving at all. In my view you have removed the most important and useful definition. I'm not going to waste time arguing with you, because it is obvious that you won't listen. Fortunately, someone else who understands physics will likely be along soon to correct your mistakes. Otherwise I will revert tomorrow.Rracecarr (talk) 16:36, 23 April 2008 (UTC)

Rracecarr, the centrifugal force that I am talking about is the one that occurs in a centrifuge. As the heavy particles in the solution are constrained to co-rotate, they experience an outward radial force which moves them to the edge.

The centrifugal force that you are talking about is a mathematical game. It doesn't exist. There is a circular motion artifact. That is all.

But thanks to PeR's message on my talk page, I can now finally see where you are coming from. Somehow, you can see in this circular motion, a resultant between a Coriolis force and a centrifugal force.

If that is official teaching, then so be it. But in that case, we really need to be introducing three centrifugal forces into the main article.

(1) The real centrifugal force such as occurs in the centrifuge when particles get thrown to the edge, or when passengers get thrown to the side door when a car swerves around a corner.

(2) Then there is the knock on effect of this which some people describe as the reactive centrifugal force. When the object in (1) presses against something, due to the centrifugal force, it transmits the effect on to that something, just as a book on a table transmits the force of gravity unto the table in the form of its weight.

(3) And finally we have this ultra mathematical nicety which contributes towards an artificial circular path as viewed from a rotating frame of reference.

Finally I know what you are talking about. But quite frankly, when a reader wants to read about centrifugal force, they will only be interested in (1), and I think that it is (1) which the article should be concentrating on.

It seems that you, PeR, and Henning Makholm have been subtely pushing (3) and are determined to keep it that way. David Tombe (talk) 17:14, 23 April 2008 (UTC)

Your (1) and (3) are the same thing. They are forces which appear when you view the world through a rotating frame of reference. It seems you would like to draw a distinction between the intuitive force (1) and the mathematical description of it (3). Rracecarr (talk) 17:46, 23 April 2008 (UTC)

Rracecarr, The only thing that viewing something from a rotating reference frame does is to introduce a circular motion artifact on top of the alreay existing motion. It does absolutely nothing else.

The centrifuge on the other hand produces a very real radial effect which is absolute, and can be viewed from any frame of reference.

So the fictitious effect which you are interested in is not the same thing as the centrifugal force as is commonly understood by the man in the street.

The man in the street sees centrifugal force as the outward radial force which occurs when an object is constrained to follow a curved path.

You are just playing out cheap mathematical games and confusing this whole article.

There is a big difference between an object that is co-rotating in a rotating reference frame and an object that is at rest in the inertial frame and viewed from the rotating frame. In the former, an actual centrifugal force accelerates the object radially outwards. In the latter, nothing happens.

If you can't see the difference between the two situations, then you are not living in the real world.

You, and PeR, and Henning Makholm are totally messing this article up to satisfy your own curiosity about irrelevent manipulations of maths.

You seem to think that there is something very interesting about the fact that the artificial circle can mathematically equate to the summation of the expression for Centrifugal force and the expression for Coriolis force.

At best, that is hardly interesting, and it's certainly not what a reader has in mind when he wants to read about centrifugal force.

But at any rate, the whole basis of this idea is faulty. Take a look at the mathematical expressions for the two fictitious forces. They both involve the angular velocity quantity ω. This angular velocity equates to v/r where v is the speed relative to the true frame.

In other words, these expressions only have any significance for objects moving at v relative to the true frame (ie. co-rotating with the rotating frame).

This can be easily demonstrated simply by looking at the centrifuge. If there is no co-rotation then the centrifuge will not operate.

This theory of yours, that a fictitious centrifugal force combines with a fictitious Coriolis force to yield a fictitious centripetal force is totally bogus.

And you are sacrificing this whole article in the name of this pet theory of yours. David Tombe (talk) 05:43, 24 April 2008 (UTC)

I am going to try not to be snippety or condescending, in the hopes that you will listen rather than simply defend. Heavy things move toward the outside of a spinning centrifuge. This effect can be understood in 2 different ways: by analyzing in an inertial reference frame (the lab) or by analyzing in a frame which rotates with the centrifuge.

In the lab frame, the stuff in the centrifuge spins in circles: it accelerates inward toward the middle of the centrifuge. A centripetal force is required to maintain this centripetal acceleration, and the heavier particles require more force, due to Newton's second law. Because it is "harder" to bend the paths of the heavier particles, they go "straighter" and move toward the outside. Intuitively, it seems there is a centrifugal force flinging them outward, but in the lab frame there really is no such force. If you write out the equations of motion, there is no term for centrifugal force--it exists only in people's imaginations.

The second way of understanding the effect is by moving to the frame with rotates with the centrifuge. In that case, the stuff inside doesn't spin around at all--it basically sits still, but again, the heavier particles move toward the outside. In this frame, the movement is caused by a centrifugal force, which arises because of the rotating frame of reference. The centrifugal force exists in this frame, in the sense that there is a term for it in the equation of motion, but it is fictitious in the sense that it only exists because we've chosen a rotating frame of reference--there is still no actual physical source of outward force. Rracecarr (talk) 18:48, 24 April 2008 (UTC)

Rracecarr, Thank you for your response. I can understand why you think like that, but you are overlooking some points.

First, I should point out that I understand that wikipedia is about presenting the official viewpoint, and if my viewpoint differs from the official viewpoint, then I will not be attempting to impose my viewpoint on the main page.

The official viewpoint regarding the centrifugal force in the centrifuge is that it is an 'inertial' force, and as such, I will not be arguing with that fact on the main page.

At the moment, I am trying to get you to see that whether the centrifugal force in the centrifuge is 'inertial' or 'fictitious' or whatever, that it is quite different from the purely fictitious effect which is an artifact of a rotating frame of reference. In the latter case, a particle that is stationary in the true frame is not being subjected to any kinds of force whatsoever.

Now even if you wish to write off the centrifuge effect as being fictitious too, you must at least admit that it is nevertheless real enough to invoke Archimedes' principle.

That alone is sufficient grounds upon which to distinguish between the two scenarios.

Regarding my own opinions on what you said, I should state that in the laboratory Cartesian frame that centrifugal force is disguised as 'Inertia'. It is the straight line motion that is the extreme hyperbola asociated with a central force orbit in which the inward gravity force is zero.

The reality of the situation is that there is a radially outward force in circular motion, no matter from what frame of reference we view it.

But that is only my opinion and I will not enforce that on the main page. Nevertheless, I believe that if you stand back and take the broader view, you will realize that there is a point here.

What I am trying to correct on the main page is the presentation, coherence and emphasis.

I want the reactive centrifugal force to be discussed as a knock on effect in the main article. There are some good citations there, but it shouldn't be clouding the introduction.

I want the introduction to focus on the 'inertial' effect that occurs in a centrifuge or when a passenger gets flung to the side door of a swerving car. I want it to refer to the general case of curved path motion and not exclusively to circular motion.

I am opposed to the emphasis that is placed on the issue of rotating frames of reference as these are not needed to observe the effect.

I am opposed to the emphasis that is placed on the artificial circular motion. That is not centrifugal force. The theory that makes out that a fictitious centripetal force results from a fictitious centrifugal force and a fictitious Coriolis force is false on a number of counts.

(1)You cannot have a centripetal force in isolation. In the radial direction, it must be balanced by centrifugal force otherwise there would be radial motion.

Yes, but radial motion can occur in general.- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)

(2)Despite what some people say, the Coriolis force does not act radially. The entire derivation is based on the principle that it is a tangential force and so it cannot act along the same line as the centrifugal force. The two forces are always mutually perpendicular.

Sorry, this is quite wrong. The Coriolis acceleration is: $-2\mathbf {\omega \times v}$. As you can see, since it is a cross-product, if v is perpendicular to r then it acts completely radially.- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)

(3)Those 'inertial' force equations are only designed to apply to objects that co-rotate. The angular velocity ω terms refer to the tangential velocity of the co-rotating object. For an object that is stationary in the true frame, those terms do not exist. David Tombe (talk) 04:31, 25 April 2008 (UTC)

Sorry, but that is wrong also. Coriolis and Centrifugal acceleration/forces apply to all objects when considered from the rotating frame of reference. They do not have to be rotating in 'reality' (i.e. as seen from an inertial frame).- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)

Actually, if you consider the *lab* from Racecarr's above example with the centrifuge, the fictitious acceleration also acts on it! So how come it doesn't fly off? It's because the coriolis force holds the lab in a circular motion around the centrifuge, because the coriolis acceleration/force is purely radial in that case!- (User) WolfKeeper (Talk) 05:21, 25 April 2008 (UTC)

Wolfkeeper, I was fully aware of the fact that the Coriolis acceleration is $-2\mathbf {\omega \times v}$. But if you ever studied the derivation of this term, you would see that it is only the tangential component that we are interested in.

No. The equation means what it says. omega is a vector aligned with the rotation axis which is of length proportional to the angular velocity, v is a vector that is aligned with the instantaneous velocity of a particle. 'x' is the cross product. There is no other valid interpretation of that equation; and it most definitely may point radially.- (User) WolfKeeper (Talk) 17:34, 25 April 2008 (UTC)

Once again, you have become fixated on this ultra fictitious scenario regarding why the background stars don't fly off due to the Earth's diurnal rotation.

No, not at all.- (User) WolfKeeper (Talk) 17:34, 25 April 2008 (UTC)

The question I am trying to address is,

can you see the difference between these two case scenarios?

(a) A stationary object as viewed from a rotating frame of reference.

(b) An object co-rotating with a rotating frame of reference hence inducing a radial centrifugal force which is real enough to invoke Archimedes' principle.

Can you see the difference between those two scenarios? David Tombe (talk) 07:02, 25 April 2008 (UTC)

You didn't answer my question (below). Explain your own theory properly, before you ask others why they think it's wrong. --PeR (talk) 07:51, 25 April 2008 (UTC)

PeR, you missed the point. This has got nothing to do with any theories of mine. I'm trying to focus your attention on the fact that swinging buckets of water over your head the not the same as the background stars describing circles across the sky.

Your team are fixated on the latter and all the mathematical games that you can play to try and argue that a stationary object has got a net summation of fictitious forces acting on it.

This article is supposed to be about the 'inertial' centrifugal force of the centrifuge.David Tombe (talk) 15:02, 25 April 2008 (UTC)

Reply to PeR

PeR, Regarding your private message to me, I should reply that you are not in a position to tell other people not to edit this page. Wikipedia is an ongoing thing. Since you didn't like my alternative version (although somebody else obviously did), I decided to fix up the existing version instead.

And you can discuss these matters on the talk page. You don't need to go private behind the scenes.

I now understand exactly where you, Henning Makholm and RRacecarr are going wrong. You can't see the difference between the situation which occurs when an object is co-rotating with a rotating reference frame, and when the object is not co-rotating.

It is only when the object is co-rotating that we get any actual effect. The situation that you like to highlight regarding the artificial circle, really is fictitious in the true sense of the word, and it is of no interest to anybody.

The situation which I am interested in is the inertial effect which occurs in a centrifuge.

In the introduction, we need to state the very basic and simple sentence that when an object is constrained to move in a curved path, it experiences a radially outward force.

The introduction cannot be allowed to focus on that obscure fictitious scenario that you seem to be so interested in, and indeed there is precious reason to even bother mentioning it in the main article.

You cannot dominate the topic with all that nonsense about a fictitious Coriolis force twice as strong as a fictitious centrifugal force causing a fictitious centripetal force. That is not what the readers are interested in.

Secondly, the reactive aspect shouldn't be in the introduction. It should be in a section in the main article.

The readers want the outward radial effect which comes from constrained curved motion. They want swinging buckets of water over the head. They want masses being swung around on the end of a string and discussions about whether they fly off radially tangentially or both, when released.

There is no need to mention rotating frames of reference because a centrifuge can be seen to have worked irrespective of which reference frame we view it from.

You are trying to cloud up this article with what you believe to be some clever realization about fictitious forces summing together to give other fictitious forces and you don't want to face up to what centrifugal force is really about. David Tombe (talk) 11:19, 24 April 2008 (UTC)

Your talk page is not behind the scenes. Anyone can read it.

Here's a part of what you wrote in the introduction:

An inertial or "fictitious" centrifugal force appears when a rotating reference frame is used for analysis, providing that the object in question co-rotates with the frame. The true acceleration on objects that are co-rotating with the frame is supplemented by a radially outward (fictitious) centrifugal force.

This effect can be extended generally to all curved path motions.

Now tell me, with your "definition" of centrifugal force, when is an object considered to be co-rotating with the frame? When it is stationary in the frame, sure. But what if it has a very small, but nonzero velocity relative to the frame? What if this speed becomes slightly larger? What if the speed in the rotating frame is so large that the object is stationary in the inertial frame? In that case you say there is no centrifugal force. Where do you draw the limit? Does your centrifugal force end abruptly, or does it phase out as the velocity relative to the rotating frame increases? Mechanics is an exact science, so please give equations explaining your theory. Also, please give a reference to the textbook where you found that equation. --PeR (talk) 18:45, 24 April 2008 (UTC)

PeR, centrifugal force exists to the extent that the motion co-rotates. Ultimately the effect can be traced to the tangential velocity with respect to the rotation axis in the laboratory frame. David Tombe (talk) 04:34, 25 April 2008 (UTC)

"to the extent that the motion co-rotates" is rather vague. Mechanics is an exact science, so please give equations with a refrence. --PeR (talk) 06:56, 25 April 2008 (UTC)

PeR, you are just pretending that you don't understand. If it doesn't co-rotate, there is no centrifugal force. The object sits still unaffected.

If it fully co-rotates, the radial centrifugal force is given by v^2/r, where v is the tangential speed.

If it partially co-rotates, the centrifugal force is given by the same equation but with the speed changed to the tangential speed of the object in question, with respect to the same rotation axis.

At the moment, you are just in denial of reality. For too long, you have had your mind focused on some irrelevant fictitious form of centrifugal force and there is a group of you closing ranks to defend that erroneous way of thinking.

I'm sorry, but you don't understand. This article is completely about that 'erroneous' way of thinking as you put it. The problem you have is a) it's self consistent b) it models reality correctly (it must do, since it's derived from an inertial frame using correct logic).- (User) WolfKeeper (Talk) 17:22, 25 April 2008 (UTC)

So far, there is you, Henning Makholm, RRacecarr, Wolfkeeper, and now FiziksFighter. I am expecting more to arrive to back you all up before this is over.

I have no doubt that you will all attempt to confound the issue with a hail of bogus mathematics. But this issue doesn't depend on maths. It depends on basic common sense.

Only a fool thinks that the background stars are being subjected to a combination of fictitious forces that result in a final inward fictitious radial centripetal force. David Tombe (talk) 16:22, 25 April 2008 (UTC)

The thing is, maths is a model of reality, not reality. In the rotating non inertial frame model that is the subject of the article, yes, yes they are. You're just going to have to live with that.- (User) WolfKeeper (Talk) 17:22, 25 April 2008 (UTC)

Article should be split

The two sorts of centrifugal force are distinct topics. Distinct topics should have their own articles- that's one of the differences between a dictionary and an encyclopedia. Just because they are called the same doesn't meant they get to go in the same article. In fact, it's wrong to have them in the same article in the wikipedia.- (User) WolfKeeper (Talk) 05:42, 25 April 2008 (UTC)

Agreed. I think there should be an article entitled Fictitious forces in a rotating reference frame, that would be a subarticle of both this one, Fictitious force, and Coriolis force. It is much easier to discuss centrifugal and Coriolis forces together than one at a time, since you rarely have one without the other. A significant portion of the current article is devoted to explaining the difference between the two meanings of the term. Perhaps it should be moved to Centrifugal force (disambiguation). Then we create a new article entitled Centrifugal force (reaction force), and leave Centrifugal force as a redirect to the disambig. For good measure we should also create a page Centrifugal force (fictitious) that redirects to Fictitious forces in a rotating reference frame. --PeR (talk) 06:47, 25 April 2008 (UTC)

Or maybe we could move this article to centrifugal force (fictitious) with a redirect from centrifugal force and split off the real force to centrifugal force (reaction force) and put a cross-reference 'for' at the top. I'm leaning against a disamb at this time, there's only two meanings and I'm pretty sure that the real force isn't being referenced very much.- (User) WolfKeeper (Talk) 17:55, 25 April 2008 (UTC)

Or possibly instead of centrifugal force (fictitious) we could move it to centrifugal effect which would talk about the acceleration, and then include the force equation as well. There just doesn't seem to be quite the same degree of garbage going on over at coriolis effect and there's more symmetry in the wiki better reflecting the physics.- (User) WolfKeeper (Talk) 18:03, 25 April 2008 (UTC)

I like Wolf 1 a lot. Not so big on Wolf 2 (centrifugal effect). It is not in such common usage as Coriolis effect, and the same discussion of acceleration can be included at both the centrifugal force articles.Rracecarr (talk) 18:13, 25 April 2008 (UTC)

Yes, I agree. I did a google on 'centrifugal effect' and it's not common enough to be an article title.- (User) WolfKeeper (Talk) 19:13, 25 April 2008 (UTC)

I also thought that the classical use of the term was uncommon these days, but I'm starting to change my mind. It seems to be used applied mechanics. And I have heard materials science people use the term correctly in the classical sense when discussing rotating parts in machinery. I think, because the term is not introduced at high-school level, people from different fields will have learned the term with different meanings, and people who learned about the fictitious kind from a theoretical physics class might never realize that people who studied statics use the same term with a different meaning. --PeR (talk) 21:50, 25 April 2008 (UTC)

Sure, if it wasn't in use, we wouldn't have it in an article. It's in the article because we found references to it, less than to the d'Alembert force version, but it's definitely in use.- (User) WolfKeeper (Talk) 22:08, 25 April 2008 (UTC)

OK, I've created Reactive centrifugal force, on reflection it seemed a better name than Centrifugal force (reactive), but we can always move it, or add redirects if necessary.- (User) WolfKeeper (Talk) 02:37, 27 April 2008 (UTC)

Good, I think. That leaves us with the question of where to explain the differences between the two meanings. They are confused often enough (and the confusion can be difficult enough to dispel) that I think it falls within our encyclopedic mandate to set the difference straight explicitly. –Henning Makholm 02:55, 27 April 2008 (UTC)

Ok, I've hacked the article a bit, I'm not totally happy with it, but it's about 60% there. I think we need to prune back the reactive force more, and probably explain more about the reactive force in its own article.- (User) WolfKeeper (Talk) 03:02, 27 April 2008 (UTC)

Agreed, though I think we may have more than 40% to go yet. The previous consensus state of the article was not quite a model of brilliance and clarity in its explanation of the fictitious force, and we should be able to do better if we don't have to do it in the context of an (apparent!) controversy between two meanings of the word. In particular, I think the "Rotating reference frames" and "Fictitious forces" sections overlap each other without good reason; they should be combined into a single section which tells it all in a logical sequence.

As for references to the reactive force, I think there should be the hatnote, plus a more verbose discussion late in the article, probably including the table of differences. I suggest that the "confusion and misconception" section might be coopted for this, and possibly be given a more encyclopedic-sounding title along the way. –Henning Makholm 03:15, 27 April 2008 (UTC)

Article should be split into three ?

It would seem now that the article should be split into three.

(a) The ultra fictitious centrifugal force associated with the mathematical games surrounding the articial circle produced by a rotating frame of refeence.

(b) The 'inertial' centrifugal force which invokes Archimedes' principle in a centrifuge and causes real differential effects on the particles in a solution observable from all frames of reference.

(c) The knock on effect that a body being acted upon by (2) has on any object obstructing its path.David Tombe (talk) 07:11, 25 April 2008 (UTC)

No. --PeR (talk) 07:48, 25 April 2008 (UTC)

Well PeR, since you have been so disagreeable up until now, I would hardly have expected any other response from you.

I will however take this matter to the wiki physics project.

The question will be put. Are these two effects the same thing?

(a) An object in the rest frame that is not co-rotating with a rotating frame appears to trace out a circle in the rotating frame. An example of this is the stars as they cross the sky at night time.

(b) When objects co-rotate with a rotating frame, a radial centrifugal force is induced which is real enough to invoke Archimedes' principle. An example is the centrifuge.

Are these two effects the same?David Tombe (talk) 08:50, 25 April 2008 (UTC)

Just make sure you include a link to this page, so that people can catch up on what has already been said. --PeR (talk) 09:24, 25 April 2008 (UTC)

Electrodynamicists edit's

Electrodynamicist, while I appreciate you reverting to that concise introduction, my own belief now is that we should be dealing with the so-called consensus version on one point at a time.

The issue ultimately comes down to the fact that some of the editors here want to focus attention exclusively on the ultra fictitious centrifugal force which they create around stationary particles just by playing around with maths, and wrongly too.David Tombe (talk) 14:48, 25 April 2008 (UTC)

New tack

Maybe we can write the article in such a way that everyone is happy. As I understand it, David Tombe is unhappy that the consensus version does not discuss in the intro, in a straightforward, plain English way, things like buckets swinging over heads. I think he may be right that such a "common sense" description is in order. However, the rest of us are not happy with phrases like outward radial force which acts on objects moving in a circular path, since such a force does not actually exist. Surely there is a wording that will satisfy everyone.

Working in that direction, I have a couple of questions for David Tombe:

1) When an elevator starts to move upward, you feel heavier. What do you call that "force"?

2) Do you acknowledge that what you call "ultra mathematical games" are, fundamentally, exactly the same centrifugal force you want the article to focus on, just expressed in a different language? Would you agree to an article that talked about water in a bucket and moved smoothly on to discuss that situation from the reference frame of the bucket, and so to fictitious forces? Rracecarr (talk) 17:52, 25 April 2008 (UTC)

Rracecarr, regarding the man being accelerated upwards in an elevator, I don't have a special name for that force. The force acts against gravity and there is a resultant upward force. It's the same as any contact force. It causes acceleration.

On the maths, I am well versed in the equations for a rotating frame of reference. But I believe that these equations can be used to cloud the underlying realities of the situation.

When a man is stationary in an inertial frame, then there is nothing happening. It is irrelevant that somebody in a rotating frame views him as travelling in a circle.

But when a centrifuge causes particles to move outwards to the edge, we have a very real effect that has caused relative motion between different particles in the solution. We have invoked Archimedes' principle.

One should be able to see that these two situations are not the same, without having to go into any maths.

At least I know now that it is because of the maths that you think that the situations are the same.

Regarding that maths, one key point is that Wolfkeeper seems to think that the cross product expression for Coriolis force proves that the Coriolis force acts in any direction. He is overlooking the fact that the cross product was introduced to be in the tangential direction with the magnitude being the product of the angular speed and a radially aligned magnitude.

Another point is that in order for circular motion to occur, we need to have a net zero radial force. In the circular artifact scenario, the forces aren't balanced

And a third point is that when you study the derivation of those equations, you will see that the angular velocity is intricately linked to the linear velocity. There has to be a physical connection between the v term and the ω term. In your artificial circle example, the stationary object has got no physical connection with the motion.

So nothing happens. It is neither centrifugal force nor Coriolis force. It is merely a circular motion artifact.

But we shouldn't need to go into this maths to have to see that. It should be obvious from a common sense premises that centrifugal force only occurs on an object which is being constrained to move in a curved path.

On your second question, I would adopt the policy that all articles should began with a simple and basic introduction but maybe brightened up with one or two obscure points of interest.

As the article progresses, I would never object to more and more complicated and specialized aspects being introduced. The issue of rotating frames of reference could be introduced as a specialized section.

The current introduction could be re-worded by giving a basic description of centrifugal force as per the kind that is experienced in everyday situations. A clarification clause should be introduced to make sure that readers don't confuse it with centripetal force.

The swerving car example could then be given. Or indeed the artificially induced gravity scenario of a rotating cylinder. But I don't believe that the knock on effect needs to be emphasized as a separate centrifugal force. It is merely what weight is to gravity.

Finally, Wolfkeeper asked why is there never a similar dispute going on at the Coriolis force page? The reason is that the discussion surrounding where Coriolis force is real and where it is fictitious, and where it doesn't exist at all is to too complicated, too controversial and too likely to break wikipedia's rules agains original research and opinion. Furthermore, even at best, the man in the street is not familiar with what Coriolis force really means, and there is no easy way to explain it without involving alot of arguments. So its best to leave that article for the time being.

Centrifugal force has a clean cut off between what is actually centrifugal force and what has been confused for centrifugal force. That is because it is a radial effect. But Coriolis force is a tangential effect and so circular motion can create an artifact which gets confused with what genuinely is a fictitious Coriolis force. Then there is the controversy surrounding where Coriolis force becomes real. So we have three stages of analysis in Coriolis force. the Foucault pendulum at the poles is only an artifact. The missile flying through the air from Miami to New York is Coriolis force but purely fictitious. Finally the atmosphere involves a v that is physically connected with an entrained ω and so the effects can be real and viewable from outer space. The latter scenario corresponds by analogy to the reality of the centrifuge where the v and the ω are physically connected. David Tombe (talk) 19:05, 25 April 2008 (UTC)

All I know is, coriolis and centrifugal force fall out of a completely valid mathematical manipulation of a general equation of motion with respect to an inertial reference frame, and in that sense at least, they are very, very real.- (User) WolfKeeper (Talk) 19:30, 25 April 2008 (UTC)

Let's stick with the elevator for a minute. The force experienced by the person in the elevator is fundamentally the same as the centrifugal force experience by particles in a centrifuge, right? Both are the result of acceleration--the only difference is that in the elevator it is linear acceleration, whereas in the centrifuge it is centripetal acceleration. Agree? Rracecarr (talk) 20:20, 25 April 2008 (UTC)

Bucket swinging over head

I agree with David Tombe, that the introduction needs to be more accessible, and that swinging a bucket over one's head is a good example. Here's a draft text:

The term "Centrifugal force" has two different meanings. The classical meaning of the term, as used by Isaac Newton and others, is to denote the reaction force to a centripetal force. In modern usage the term can also be used to denote a fictitious force that occurs in a rotating reference frame.

An example of the classical use of the term is the statement.

When swinging a bucket over your head, the bucket pulls on your hand with a centrifugal force.

The hand exerts a centripetal force (action) on the bucket, and the bucket in turn exerts a centrifugal force (reaction) on the hand.

In contrast, an example of the modern usage would be:

When swinging a bucket of water over your head, the water stays in place due to the centrifugal force.

This sentence considers a reference frame that rotates with the bucket. (In an inertial reference the water could not be said to "stay in place", since it is moving in a circle along with the bucket.) The force referred to here is a fictitious, or pseudo force that is not caused by physical interaction, and therefore has no corresponding reaction force in the rotating frame. It is simply a mathematical construction that makes a it possible to describe the system as seen from the bucket's perspective.

I'll work it into the introduction once the edit war there has ceased.

--PeR (talk) 21:28, 25 April 2008 (UTC)

This looks good, PeR. How about removing the hand from the example:

The term "Centrifugal force" has two different meanings. The classical meaning of the term, as used by Isaac Newton and others, is to denote the reaction force to a centripetal force. In modern usage the term can also be used to denote a fictitious force that occurs in a rotating reference frame.

An example of the classical use of the term is the statement.

When swinging a bucket of water over your head, the water pushes on the bucket with a centrifugal force.

The bucket exerts a centripetal force (action) on the water, and the water in turn exerts a centrifugal force (reaction) on the bucket.

In contrast, an example of the modern usage would be:

When swinging a bucket of water over your head, the centrifugal force acting on the water causes it to stay in place.

This sentence considers a reference frame that rotates with the bucket. (In an inertial reference the water could not be said to "stay in place", since it is moving in a circle along with the bucket.) The force referred to here is a fictitious, or pseudo force that is not caused by physical interaction, and therefore has no corresponding reaction force in the rotating frame. It is simply a mathematical construction that makes a it possible to describe the system as seen from the bucket's perspective.

Rracecarr (talk) 21:44, 25 April 2008 (UTC)

Better with the removed hand, but I like my version better for the second quote. (Shorter, less complex). --PeR (talk) 22:10, 25 April 2008 (UTC)

I thought it was important to emphasize a difference between the two quotes: in the first the force acts on the bucket, in the second, it acts on the water. Rracecarr (talk) 22:22, 25 April 2008 (UTC)

Yep. On second thought, I like your version better for both quotes. --PeR (talk) 22:24, 25 April 2008 (UTC)

You guys need to actually read Newton's book since what you say here is wrong. From reading what is written here, I see what you dont know what you are doing and dont understand the arguments involved at all. Obviously this means the article does need major changes to correct the misconceptions of the editors who wrote the so called consensus version. I also suggest you actually educate yourselves before writing any more articles for wikipedia.72.64.46.3 (talk) 23:13, 25 April 2008 (UTC)

Maybe it is you, David Tombe, who needs education. That would seem the more likely possibility, since you are the only one who thinks the above is wrong. Rracecarr (talk) 02:57, 26 April 2008 (UTC)

Rracecarr, I think we need to be quite clear about this. I am not the anonymous writing from 72.64.46.3 David Tombe (talk) 07:16, 26 April 2008 (UTC)

Silly of me. Why would I assume that about 4 anon IPs, all in the Hampton, VA, USA area, doing your reverting for you and answering questions aimed at you, none of which has ever contributed to any other articles? Rracecarr (talk) 16:04, 26 April 2008 (UTC)

Actually, I think the rude anon in Hampton, VA, might be someone else. (Possibly a friend of David's.) The recent edits by User:58.10.103.101, is from a different country, and David has signed contributions from that country in his own name before. --PeR (talk) 16:24, 26 April 2008 (UTC)

Yes, I knew 58.10.103.101 was David, but that does not mean the VA anon isn't. Still, I have struck the sarcastic comment, and I will keep my other suspicions to myself. Rracecarr (talk) 16:31, 26 April 2008 (UTC)

Interesting to note that the VA anon is now prefixing a "Mr" to usernames. That is something that David Tombe used to do last year... --PeR (talk) 17:41, 1 May 2008 (UTC)

VA anon = User:Electrodynamicist, beyond a shadow. Rracecarr (talk) 23:28, 2 May 2008 (UTC)

Replies to RRacecarr, PeR, and Wolfkeeper

Rracecarr, the upward force that the elevator floor is applying to the person inside the elevator is definitely not the same kind of force as the centrifugal force which causes the heavier particles to move outwards in a centrifuge.

It is exactly, precisely the same kind of force. In the elevator, the acceleration producing the "force" is linear. In a centrifuge, it is centripetal. That is the only difference. If you had an elevator that would continue to accelerate hard for a long while, it would work just as well as a centrifuge for separating particles, and for just the same reason. If you can understand that, I think a lot of the problems we're having will go away. Rracecarr (talk) 16:20, 26 April 2008 (UTC)

I looked at your new edits. I noticed that you emphasized the fact that the inward centripetal force is being caused by an object. That immediately tells me that you are leading towards a point, with that point being almost certainly related to the issue of action and reaction.

I think that one of the big mistakes that people are making here is in actually trying to decide which force is the action and which force is the reaction. We don't need to bother doing that. When an object moves in a circle, the outward centrifugal force and the inward centripetal force will always be balanced.

I actually agree with you here. There is technically no way of defining which is the action and which the reaction. The thing that is important to remember is that the centripetal force acts on the object moving in a circle, but the centrifugal force does not. It acts on the thing exerts the centripetal force on the object moving in a circle. Rracecarr (talk) 16:20, 26 April 2008 (UTC)

You must also remember that the centripetal force does not have to be caused by an object. It could be caused by gravity, electrostatics, or indeed the Lorentz force.

On a macroscopic scale, it is ALWAYS caused by the forces you mention--gravitational or electromagnetic. The other kinds of force only act over microscopic distances. But gravitational and electromagnetic fields do not occur in isolation. They are the result of masses and charges. So yes, the centripetal force is always exerted by an object, and that object is always subject to a reactive centrifugal force. Rracecarr (talk) 16:20, 26 April 2008 (UTC)

Therefore, always remember to make your point in the most general way.

The most general way of describing a centrifugal force is that it is an outward force which occurs when any object is constrained to move in a curved path.

On what does this force act? You need to be clear. Rracecarr (talk) 16:20, 26 April 2008 (UTC)

I hope that you can now understand why we don't need to differentiate between a centrifugal force and a reactive centrifugal force, especially in the introduction. I tried to make that simple statement, I then added the fact that we shouldn't confuse it with centripetal force, and I finally stated that whereas in former times, centrifugal force was considered to be real, the modern day view is that it is fictitious.David Tombe (talk) 06:52, 26 April 2008 (UTC)

Wolfkeeper, I know exactly the derivation that you are talking about. I am very familiar with it. But never lose track of the physical reality to which it applies. There are two key aspects of this maths which you are overlooking,

(1) The Coriolis term is specifically derived to be in the tangential direction. It is a tangential effect arising from a radial motion, whereas the centrifugal force is a radial effect arising from a tangential motion.

(2) The maths only has physical meaning when v and ω are physically connected. For centrifugal force this means co-rotation. For Coriolis force, this means that v has a physical connection with the source of the rotation, such as is the case with the hydrodynamics of cyclones, or with a Foucault pendulum at mid-latitudes.

In the case of there being no physical connection, such as with a missile or a bird flying over a children's roundabaout, then there will be a fictitious Coriolis force, but only acting on radial motion. The artificial effect which acts on tangential motion in the unconnected state is not even Coriolis force.

It's all very well coming up with this maths, and the maths is indeed correct. But never lose sight of the physical meaning of the maths. David Tombe (talk) 07:03, 26 April 2008 (UTC)

PeR, Unlike with Coriolis force, centrifugal force is something that the public are more aware of. The swerving car will almost certainly be the first situatation in which a child will become subconsciously aware of it, whereas the bucket of water being swung over the head will be the first situation that will draw attention to it. The centrifuge as an engineering tool will follow on at high.

So either the bucket of water or the swerving car make good examples in the introduction. But we must first state the general description of the centrifugal force.

Take note of what I said above to Wolfkeeper. Neither centrifugal force nor Coriolis force are the artificial tangential effects which are viewed from a rotating frame of reference. You clouded your point up when you started introducing this dimension.

You began good and gave an example of centrifugal force showing that the water in the bucket was defying gravity. Then you contradicted yourself by trying to argue that in the rotating frame there was no such force. Of course there is. David Tombe (talk) 07:14, 26 April 2008 (UTC)

PeR, I just looked at your last paragraph again. You are very badly confused. You are equating the water in the swinging bucket with the ultra fictitious artificial circle produced when a stationary object is viewed from a rotating frame of reference. The latter inolves no forces at all. In the water in the bucket, centrifugal force causes pressure.

People can be hurt by centrifugal force, but nobody has ever been hurt as a direct result of being viewed from a rotating frame of reference.David Tombe (talk) 07:23, 26 April 2008 (UTC)

Reply to FyzixFighter

FyzixFighter, You have endorsed Rracecarr's latest edits. Let's look at it,

"A mass undergoing circular motion constantly accelerates toward the center of the circle. This centripetal acceleration is caused by a centripetal force, which is applied to the mass by some other object. In accordance with Newton's Third Law of Motion, the mass exerts an equal and opposite force on the object. This is the real or "reactive" centrifugal force: it is directed away from the center of rotation, and is exerted by the rotating mass on the object which imposes the centripetal acceleration. Although this sense was used by Isaac Newton,[1] it is only occasionally used in modern discussions.[2][3][4][5]"

Would you agree that centripetal force can by cuased other than by contact action from an object? For example gravity, electrostatics, or the Lorentz force.

Would you agree that this passage could be simply stated as,

"When an object moves in circular motion, the centripetal force and the centrifugal force are balanced" ?

Why not actually think about the issues before joining up with a team for an edit war? Let's see you here in the debate. David Tombe (talk) 07:37, 26 April 2008 (UTC)

I just woke up and wow... I don't want to derail the already existing conversation so I'll just answer up here. No, I would not say that the centripetal force and centrifugal force are balanced because in order for two forces to "balance", they must be acting on the same object. The two forces in this case are not acting on the same object so saying they are balanced makes no sense. They are equal and opposite, but that does not mean they are balanced. We do not say that the force of the earth on the apple is balanced by the force of the apple on the earth as the earth falls. Now frankly, it's not up to us to explain classical mechanics to you. You cry foul when we don't have a reference, yet you have never provided a reliable source that says there are three types of "centrifugal force" - you invoke common sense, but in my experience common sense is not a reliable source. By the way, here's a few references for the two types of centrifugal force - "A Dictionary of Physics", pg 57, Oxford ; New York : Oxford University Press, 1996 and "McGraw-Hill Dictionary of Physics", pg 77, New York : McGraw-Hill, 1984. --FyzixFighter (talk) 16:29, 26 April 2008 (UTC)

You say that an object moves in a circle when forces are balanced. I think I read somewhere that it would move in a straight line. Is that a statement you found in a book, or one that you made up yourself? --PeR (talk) 07:39, 26 April 2008 (UTC)

No PeR. I said that when something moves in a circle, the radial forces are balanced. You completely twisted what I said because you are now realizing that you have been totally wrong all along. David Tombe (talk) 07:42, 26 April 2008 (UTC)

No, I honestly don't understand what you mean. In your mind, what forces are acting upon the object that moves in a circle? Could you list them all, and say what they sum up to? --PeR (talk) 07:52, 26 April 2008 (UTC)

PeR, when an object is moving in a circle, there is a centripetal force acting inwards radially and a centrifugal force acting outwards radially. The inward centripetal force could be supplied by anything from tension in a string, to pressure from the floor of a rotating cylinder, or to gravity, electrostatics, or the Lorentz force.

At any rate, if the motion is circular, the centrifugal force exactly cancels with the centripetal force because there is zero radial acceleration.

If however the two forces are not balanced, the resulting motion will be more complicated. The most well known case is in planetary orbits. In a Keplerian ellipse, parabola or hyperbola, the outward centrifugal force does not balance with the inward gravitational force. David Tombe (talk) 09:45, 26 April 2008 (UTC)

(Let's just talk about circular motion for the time being.) You say there is "zero radial acceleration". Do you mean that the circular motion is due to acceleration in some other direction? (If so: Which direction? What causes that acceleration?) Or are you saying that an object can deviate from a straight line without acceleration? --PeR (talk) 10:45, 26 April 2008 (UTC)

PeR, We have not addressed the issue of how the object came to be moving in circular motion. We are merely focusing on the fact that when an object is already moving in circular motion that there can be no net radial acceleration, otherwise it wouldn't be circular motion. Hence the centrifugal force and the centripetal forces will be balanced.

You will never understand this issue if you continue to focus your attention on the special case of circular motion. I suggest that you study the general case of motion that results when an inward radial gravity force acts in tandem with an outward radial centrifugal force.

There are many possible results in terms of size, direction etc. all dependent on the initial conditions. But all solutions will come down to either an ellipse, a parabola, or a hyperbola, The circle is just a special case.

And so yes, it is possible to have an obect moving in a curved path with no net acceleration if that curved path forms part of a circle. David Tombe (talk) 11:20, 26 April 2008 (UTC)

You say:

...it is possible to have an obect moving in a curved path with no net acceleration if that curved path forms part of a circle.

Now, most textbooks define acceleration as "rate of change in velocity". Do you use a different definition? Or do you propose that an object moving in a circle never changes its velocity? --PeR (talk) 12:06, 26 April 2008 (UTC)

Again I say you need to learn some physics. The velocity does not change only the direction changes. Your understanding is limited. You need to recuse yourself from editing, along with the rest of the fools here, because you obviously dont know physics.71.251.185.86 (talk) 13:29, 26 April 2008 (UTC)

PeR, A centripetal force alone cannot cause a circular motion. It can do so only in conjunction with a centrifugal force. The two of them act together in tandem and maintain the object in the tangential direction while maintaining the tangential speed. The net radial acceleration is zero.

Consider a weight being swung around in a circle on the end of the string. The tension which supplies the inward centripetal force only comes into existence as a reaction to the outward centrifugal force.

That is in total contrast to all the assertions that had been made on the main page falsely saying that centrifugal force is a reaction to a centripetal force. In the case of the weight on the end of the string, it is the other way around. David Tombe (talk) 13:50, 26 April 2008 (UTC)

David, I'd really like to hear your answer to my question above. Feel free to answer here, or on your talk page. --PeR (talk) 14:41, 26 April 2008 (UTC)

PeR, I go along with the official definition of acceleration. Now using the very same maths that you use to promote your theories about the rotating frame of reference, we consider a position vector in the radial direction. Differentiate it. It is a product because it involves the unit vector which has to be dealt with separately to account for direction change.

The final result is an expression for acceleration in the radial direction and acceleration in the tangential direction. The tangential direction contains the Coriolis force but we are not interested in that right now.

When the centrifugal force, which is always radially outwards, is balanced by another inward radial force, then we will have zero radial acceleration and hence circular motion.

If there is no tangential acceleration and hence no angular acceleration, then we will have a net zero acceleration for an object moving in a circle.David Tombe (talk) 14:49, 26 April 2008 (UTC)

You say we have zero net acceleration, so by the textbook definition, zero change in velocity. Velocity includes direction of movement, so you are saying that an object can move in a circle without changing its direction of movement? Or do you use a different definition of velocity? --PeR (talk) 15:28, 26 April 2008 (UTC)

Look at the old talk archive -- it appears that David still insists on taking unadjusted coordinate accelerations in a polar coordinate system. That's how he thinks uniform circular movement has no net acceleration. –Henning Makholm 01:08, 27 April 2008 (UTC)

If I can also jump in, David take that same analysis that you just put above to looking at what kind of acceleration is required for circular motion. But let's not start out at the position vector, let's go right to the velocity vector. The velocity vector in constant circular motion is v*theta_hat, where v is a constant. Differentiating this with respect to time gives 0*omega_hat+v*d(omega_hat)/dt. Now when you go through the math for the unit vectors, you will find that d(omega_hat)/dt is -d(omega)/dt*r_hat (honestly this is a lot easier to see when done in cartesian unit vectors, and will yield the same results - most calculus-based, freshman physics textbooks go this route). So even though the motion is circular, the acceleration is radial. I'm guessing though that you're going to disagree with me on the d(omega_hat)/dt = -d(omega)/dt*r_hat bit. --FyzixFighter (talk) 16:52, 26 April 2008 (UTC)

FyzixFigher, Sorry for the late reply. Yes, in the Cartesian frame there will be inward radial acceleration in circular motion in conjunction with inertia, which is essentially outward centrifugal force under another name. David Tombe (talk) 15:22, 28 April 2008 (UTC)

Whether you use cartesian unit vectors (x_hat and y_hat) or cylinderical unit vectors (r_hat, theta_hat), the net acceleration in the inertial frame of reference is always radially inward. It is only when you go to a non-inertial frame that fictitious forces, such as the Coriolis and centrifugal force, appear for F_net=m*a to be true for those rotating coordinates. Inertia is not a force - if this is the crux of your argument (as it would appear to me), then provide a reliable source that says as much. The same applies for everything else, provide a reliable source that describes the centrifugal force as a real, physical, non-fictitious source or your edits will continue to be reverted. The talk page is not here to debate whose view of physics is correct, nor to try to teach correct physics. --FyzixFighter (talk) 15:40, 28 April 2008 (UTC)

Reply to PeR and FyzixFighter

You wish to look at the picture from an inertial Cartesian reference frame thinking that the centrifugal force will disappear.

In an inertial Cartesian reference frame, a particle in circular motion will indeed have an acceleration. The direction of the particle's velocity is constantly changing. It will have an acceleration always pointing in towards the centre of the circle.

That inward acceleration will be in the radial direction in relation to the circle itself. The outward centrifugal force will still be there too in the radial direction. It doesn't go away. Both of these forces exist in the radial direction.

The reality of the centrifugal force as an absolute fact can be proved because the effects of a centrifuge are observed by both somebody riding on the centrifuge and by a person sitting in the corner of the room.

From the tangential/radial perspective, there is no acceleration. The centripetal and centrifugal forces exactly cancel.

From the inertial Cartesian perspective, these same two forces work in tandem to cause the acceleration that changes the direction of the particle, but not its speed.

There is no question of having the centripetal force acting alone. In some cases, such as the weight being spun on the end of a string, the centripetal force is only activated by the centrifugal force.

If the string were to be replaced by a spring, we could have an elliptical motion in which the two forces alternate their magnitudes.

You cannot make the very real centrifugal force vanish simply by viewing the picture from the laboratory frame. David Tombe (talk) 05:37, 27 April 2008 (UTC)

Reply to Rracecarr

Rracecarr, regarding the elevator, the correct analogy that you are looking for is,

(i) Centrifugal force is to gravity,

whereas,

(ii) Centripetal force is to 'Normal Reaction'.

You will have to learn to generalize your approach and not confine the study to circular motion, and contact forces in which the centrifugal force is causing a pressure. David Tombe (talk) 05:43, 27 April 2008 (UTC)

General Comments on Splitting the Article

This split has been motivated as a knee-jerk reaction to save face on realizing that the so called consensus version contained many errors. It has effectively moved the one and only centrifugal force off to a new page.

The remaining page deals with a pure artifact that arises from a misinterpretaion of mathematics, and it describes neither centrifugal force nor Coriolis force.

The real centrifugal force has now been labelled as 'Reactive centrifugal force' in a separate article, when in fact there are many scenarios when it is clearly not a reaction.

Take planetary orbital theory as an example. The centrifugal force is not acting as a reaction to gravity. It acts in tandem with gravity to yield elliptical orbits.

An object being swung around on the end of a string induces the tension in the string to provide the centripetal force. Clearly in this scenario, the centrifugal force is the pro-active force.

The situation is now a worse mess than ever.David Tombe (talk) 06:10, 27 April 2008 (UTC)

Reductio ad absurdum

David, in our previous discussion, you started with the hypothesis

When an object moves in circular motion, the centripetal force and the centrifugal force are balanced

and that lead you to the conclusion

...it is possible to have an object moving in a curved path with no net acceleration if that curved path forms part of a circle.

Now you are saying

In an inertial Cartesian reference frame, a particle in circular motion will indeed have an acceleration. The direction of the particle's velocity is constantly changing. It will have an acceleration always pointing in towards the centre of the circle

which means that your previous conclusion was false. My question to you is then: Was your initial hypothesis also false? Or was there an error in one of the steps from the hypothesis to the conclusion? In that case: Which step?

--PeR (talk) 06:34, 27 April 2008 (UTC)

PeR, using radial and tangential coordinates, there is no net acceleration in circular motion. Using Cartesian coordinates there is.

But the underlying reality that you are denying is that in either case, the motion in question is the result of a centripetal force acting in tandem with a centrifugal force.

You are desperately trying to make centrifugal force go away. Your colleagues have now even moved it to a separate page.

You need to study planetary orbital theory. Two forces combine together to yield an ellipse, a parabola, or a hyperbola. The circle is a special case of the ellipse. You cannot make the centrifugal force go away by focusing attention on circular motion in a Cartesian reference frame. David Tombe (talk) 08:07, 27 April 2008 (UTC)

You didn't answer my question. --PeR (talk) 08:16, 27 April 2008 (UTC)

PeR, your question was based on the supposition that my previous assertion had been false. My previous assertion that it is possible to have circular motion with no acceleration is a correct assertion. It occurs when we view circular motion in terms of radial and tangential coordinates.

Changing to different coordinate systems can change accelerations. But it can never change the reality of absolute effects such as Archimedes' principle occuring in a centrifuge. David Tombe (talk) 08:47, 27 April 2008 (UTC)

I'm still not sure what you mean. Are you saying that your previous statement

the centripetal force and the centrifugal force are balanced

only is true when viewed in "radial and tangential coordinates", but not in stationary Cartesian coordinates?

--PeR (talk) 09:00, 27 April 2008 (UTC)

PeR, in Cartesian coordinates, in the special case of circular motion, the combined effect of the centrifugal force and the centripetal force is to cause that circular motion. The combination changes the direction of the object without effecting its radial speed. It's up to you whether or not you want to call that 'balanced'. But at the end of the day, it has got no bearing on the main issue. Centrifugal force has to be present in circular motion. You are trying to argue to the contrary. You are trying to tell me that we can have circular motion with a centripetal force alone.

Consider the special case of a circular gravity orbit as viewed from a Cartesian frame. If the centrifugal force ceased, then the gravity force that had been acting as the centripetal force would bring the object straight to the center. A circular motion cannot contain only a centripetal force. It has to have both a centripetal force and a centrifugal force. David Tombe (talk) 09:16, 27 April 2008 (UTC)

According to the article on force, there are only 4 types of fundamental forces. In the example you just provided, the centripetal force is gravitational. Which type is the centrifugal force?Rracecarr (talk) 15:42, 27 April 2008 (UTC)

By "balanced" it thought you meant "the sum of the centrifugal force and the centripetal force is zero". If that is not what you meant, then please clarify. What, according to you, is the sum of the forces acting on an object that moves in a circle in a stationary Cartesian coordinate system? --PeR (talk) 09:27, 27 April 2008 (UTC)

PeR, for the purposes of this discussion, the only thing that matters is that the two forces are balanced in radial and tangential coordinates. Your entire argument about the artificial circle is explained in radial and tangential coordinates, and in that case, the two forces are definitely not balanced.

We are not going to cloud the issue by discussing it all in Cartesian coordinates. Have you ever seen the expression for centripetal force written in Cartesian coordinates? —Preceding unsigned comment added by David Tombe (talk • contribs) 07:42, 28 April 2008 (UTC)

Of course I have seen an expression for the centripetal force in Cartesian coordinates. You can find one in almost any physics textbook. So now you are saying that your statement

the centripetal force and the centrifugal force are balanced

only is true when viewed in "radial and tangential coordinates", but not in stationary Cartesian coordinates?

Or do you prefer to say that you don't understand what's going on in Cartesian coordinates, and we keep the discussion in "radial and tangential coordinates"?

--PeR (talk) 09:17, 28 April 2008 (UTC)

fx = -cos(wt) m r w^2, fy = -sin(wt) m r w^2; trivially obtained by differentiating twice with respect to time: x=r cos(wt) + cx, y=r sin(wt) + cy, where r = radius, w is the angular speed of the mass about its center, t is the time, (cx,cy) is the rotation center. I didn't even need to look it up.- (User) WolfKeeper (Talk) 09:27, 28 April 2008 (UTC)

Yes Wolfkeeper, I didn't even need to look it up either. I was only asking had you ever actually seen it been used. PeR is trying to cloud this issue by introducing Cartesian coordinates which are seldom used in this topic. A coordinate system cannot chnage the reality of a situation. The centrifuge works whether you describe it Cartesianly or polarly. It works whether you call it inertia or centrifugal force. But one thing is sure. Centrifugal force only arises when we have real rotation of the object in question. David Tombe (talk) 10:37, 28 April 2008 (UTC)

So, David, now that you have seen an expression for the centripetal force in Cartesian coordinates, will you finally answer my question: What, according to you, is the sum of all forces acting on an object that moves in a circle in a stationary Cartesian coordinate system? --PeR (talk) 13:15, 28 April 2008 (UTC)

PeR, in the Cartesian inertial frame, an object describing a circle experiences centripetal force and inertia. Inertia is another word for centrifugal force. David Tombe (talk) 14:01, 28 April 2008 (UTC)

That wasn't an answer to my question. --PeR (talk) 15:09, 28 April 2008 (UTC)

PeR, the sum of all forces in a circular motion in the Cartesian frame is a change in direction without a change in speed. There was absolutely no point to your question. It was just an attempt at verbal witchcraft to deflect the issue from the reality of centrifugal force. David Tombe (talk) 15:26, 28 April 2008 (UTC)

What I meant by the word "sum" is the mathematical vector sum of the two forces that you mention. The vector sum of two forces will be another force that can be measured in Newtons. The change in velocity that you give as an answer would be measured in meters per second.

Perhaps it would be clearer if we put numbers on everything:

Consider an object, with the mass of one kilogram, that is swung on a rope in a gravity-free and frictionless environment, so that it moves in a circle with a radius of one meter, with an angular velocity of one radian per second, as seen from an inertial (stationary, non-rotating) reference frame. What are the centripetal/centrifugal/other forces (magnitude and direction) acting on that object as seen from that reference frame? What is their vector sum? What is the acceleration of the object?

Rest assured that there is no "witchcraft" going on here. I simply want to pinpoint exactly where our views differ. I'll give you my answer to the questions first:

Answer according to User:PeR

* Centripetal force acting on the object = 1 N, directed towards the center of rotation. (This force is provided by the rope.)

* Centrifugal force acting on the object = 0. (There is no centrifugal force acting on the object.)

* Other forces acting on the object = 0. (There are no other forces in this example.)

* Vector sum of the above forces = 1 N, directed towards the center of rotation.

* Acceleration of the object = 1 m/s^2, directed towards the center of rotation. (Because F = ma).

Now, just so there's no misunderstanding, I'd like you to replace the question-marks in the table below with magnitude/direction pairs.

Answer according to User:David Tombe

* Centripetal force on the object = -1 N

* Centrifugal force on the object = 0

* Other forces acting on the object = 0

* Vector sum of the above forces = 1 N

* Acceleration of the object = 1 m/s^2, directed towards the center of rotation.

Note that my answer will be the same regardless of whether Cartesian coordinates or polar coordinates are used. If your answer will be different depending on coordinate system, then please make one copy of the answer table for each coordinate system.

I've tried to make the example as simple as it could be while still highlighting our different views. Your input will be appreciated.

--PeR (talk) 09:12, 1 May 2008 (UTC)

PeR, My answers are inserted above. There will be no net acceleration as viewed in tangential/polar coordinates, but in the inertial frame, there will be exactly as you say, an acceleration of 1m/s^2 directed into the centre of the circle.

But we don't actually need to be arguing about this. Let's just say for the sake of argument that a stationary object as viewed from a rotating reference frame traces out a circle and that you are correct that fictitious forces combine to create a fictitious centripetal force. I don't actually agree with that at all, but let's accept it anyway for the sake of argument.

I have accepted that applied maths courses teach the doctrine that those rotating reference frame equations apply to all particles, irrespective of co-rotation. I did the course myself many years ago.

I decided to compromise and accept the wording of the first sentence in the existing introduction which sates the above fact. Personally, I see no need to cloud the issue with rotating frames, but I have decided to accept that line since it is in the modern maths books.

I then decided to draw attention to the fact that when co-rotation does actually occur, that we will get an actual radial acceleration or an actual hydrostatic pressure. That is the centrifugal force that the man in the street is looking for.

But Wolfkeeper instantly reverted it on the false premises that I was suggesting that centrifugal force only occurs in co-rotation.

When his error was pointed out, he dug in and stuck to his position.

He is now trying to deny hydrostatic pressure in a rotating bucket.

That is what the argument is about now.

I have offered up a perfectly good compromise introduction that covers all the key points accurately, but Wolfkeeper is behaving totally irrationally.

So I have a question for you. Is the hydrostatic pressure in a rotating bucket an absolute reality, or is it only something which we view from a particular frame of reference?

Also, do have a look at my new introduction because I'd be interested to hear exactly what aspects of it you disapprove of. It would have neatly tidied up the whole reactive centrifugal force thing.David Tombe (talk) 09:37, 1 May 2008 (UTC)

I'm still confused. The question was regarding an intertial frame, and you filled in "Acceleration of the object = 0". But then you immediately state: "in the inertial frame, there will be exactly as you say, an acceleration of 1m/s^2 directed into the centre of the circle." Which is it?

--PeR (talk) 09:50, 1 May 2008 (UTC)

Regarding your new introduction: I have read it. It is getting better compared to your initial attempts, but it still misses a few key points, for example you keep removing the link to fictitious force, which is a term that is vital to the subject. I think you'd be much more productive if you worked on it here on the talk page. In article space, it'll just keep getting reverted because of the inaccuracies.

By the way, the title of this section, reductio ad absurdum, essentially means if your initial hypothesis leads you to state that "one equals zero", then your initial hypothesis was false.

--PeR (talk) 10:12, 1 May 2008 (UTC)

PeR, I realize now that it was the inertial frame that your box was for. Sorry, I answered as if it was for radial/tangential. I will correct it now. My answers for 'inertial frame' are the same as yours.

On the other issue, you mentioned inaccuracies. Can you please point out those inaccuracies. I don't actually believe that you are genuine. You have given yourself away by having stated that the term 'fictitious' is essential. Why should the term fictitious be so essential for the situations concerning actual radial acceleration and hydrostatic pressure?

I think you are in the same boat as Wolfkeeper. You are living in a fictitious world of denial. You will do anything to make sure that there is nothing in the introduction to this article that might lead anybody to suspect that centrifugal force might be real.

You are in a conspiracy with Henning Makholm, FyzixFighter, and Wolfkeeper to impose a false view of reality through the wikipedia pages.

There are no inaccurate facts in my new introduction, and for you to say so is a downright lie. The truth is that you are offended by references to the co-rotation scenario where actual hydrostatic pressure is induced. That is a real absolute effect. It is frame independent, and it doesn't fit in nicely with you fictitious view of the world where everything is relative and there are no absolutes.

So you are trying to suppress this fact. That's what it all comes down to. You are platooning in superior numbers with a group who know alot more about how to manipulate the wikipedia rules and regaulations than they know about physics.

All this rubbish above about 'what is the acceleration in the inertial frame' is an irrelevant decoy to enable you to obfuscate the whole issue.David Tombe (talk) 10:29, 1 May 2008 (UTC)

So now you do agree that there is no centrifugal force when using an inertial frame of reference. That is very good. We are half-way to agreement. Now, when you say "radial/tangential", do you mean a set of coordinate axes that rotates so that the radial coordinate axis always points to the object? Is it OK by you if we refer to that as a "rotating coordinate system"? If we were to color-code the forces, so that forces that are the same in any reference frame are called "blue" forces, and forces that are zero in an inertial frame, but exist in a rotating frame are called "red" forces, would you then agree with the statement: the force from the rope is a "blue" force, and the centrifugal force is a "red" force? --PeR (talk)

P.S. Please stop writing insults to your fellow editors. We might think you're trolling. --PeR (talk)

PeR, I hope we're going to get to the point of this soon. My ultimate argument will be that centrifugal force is absolute and doesn't depend on frame of reference. It is an outward radial effect. It doesn't matter how we view it.

What you are doing is trying to fudge the issue by looking at it in Cartesian coordinates. In Cartesian coordinates, centrifugal force becomes inertia. Now I know that you will immediately say that inertia is not a force. But that then drags us into a conversation on original research and we don't need to go down that road.

In the Cartesian frame, which incidentally I don't believe exists in real life, centrifugal force in the presence of a negligible central force of attraction such as gravity, will result in a highly eccentric hyperbolic motion. This approximates to the straight line.

We call straight line motion inertia. It is the tendency to move in a straight line at constant speed unless some other force acts.

Hence if we analyze circular motion in a Cartesian frame the centripetal force will act in addition to inertia(centrifugal force) and cause a radially inward acceleration which changes the dircetion but not the speed of the particle. Basically the centripetal force causes the particle to deviate from its straight line path, as per inertia.

But we are way behind now with the main argument. First can you tell me where the 'point of view' material is in my proposed introduction. I guarantee that you can't do that. It is a false inuendo. you are basically referring to the clauses that illustrate true facts that are not convenient for the term 'fictitious force'.

On your specific question, both those forces are radial so they both have to be the same colour. I say that they are both blue. They both always exist at any time in the radial direction. Even in the Cartesian frame, they both exist in the radial dircetion.David Tombe (talk) 13:19, 1 May 2008 (UTC)

Previously you said:

I answered as if it was for radial/tangential. I will correct it now. My answers for 'inertial frame' are the same as yours.

and changed the "centrfiugal force" from one Newton to zero.

Now, if it is true that "centrifugal force is absolute and doesn't depend on frame of reference" then why did you change your answer?

Also, if the centrifugal force doesn't depend on frame of reference, then what is it, one Newton or zero? (The answer you have filled in now, above, is zero. To me that's the same thing as saying it doesn't exist in that frame of reference.)

--PeR (talk) 13:56, 1 May 2008 (UTC)

PeR, Can you get to the point please. In radial coordinates the centrifugal force and the centripetal force balance in circular motion. That's all we need to know. In Cartesian coordinates, the physics doesn't change but the way we describe it all changes. In Cartesian coordinates, there is no radial direction. It doesn't actually matter about Cartesian coordinates. The reason why you keep concentrating on Cartesian coordinates is because you know it is more complicated and you can see an opportunity to cloud the whole issue.

Basically you are hoping to be able to conclude that in Cartesian coordinates in circular motion, we have centripetal force only and no centrifugal force. You are then going to go to your artificial circle scenario and try and reason that we could therefore have centripetal force only in that case too. But you can't do that. There was inertia in the Cartesian scenario for the real circular motion. In your artificial circular motion there is no inertia, and anyway, in radial coordinates the forces in your artificial scenario are not balanced.

Your theory is wrong. It is wrong because the equations only apply to co-rotation, and to radial velocity for Coriolis purposes, and when misapplied as in the artificial circle scenario, the forces don't even balance.

I am not going to look any more at Cartesian coordinates simply for you to confuse the issue and make false conclusions because that's exactly what you are trying to do.

And you don't need to look at the maths at all to know that your theory is wrong. The fact that hydrostatic pressure can be generated in a rotating bucket is sufficient to show that a real effect occurs in co-rotation which does not occur when something stationary is viewed from a rortating frame. David Tombe (talk) 15:08, 1 May 2008 (UTC)

Reply to Racecarr regarding the centrifuge

Rracecarr, in the centrifuge, heavier particles actually move past lighter particles. This is a real effect which is observed from every frame of reference. For this effect to occur, a force must be acting and it cannot be centripetal force because the particles have not yet contacted the reaction surface, notwithstanding the fact that centripetal force is in the wrong direction anyway.

The fictitious circle that you are emphasizing is not the same situation at all. It is merely an artifact.

The maths which you believe unites the two situations is only applicable when the v and the ω are physically connected. That follows from the derivation. And if you study the derivation, you will see that when the velocity formula is expanded into the acceleration formula, the v in the v times ω term gets replaced with another v which is only radial.

In other words, that maths does not apply to the artificial circle. You have unanchored the maths from the physical reality to which it applies. David Tombe (talk) 06:20, 28 April 2008 (UTC)

Since you didn't answer me above, I copy and paste:

[David Tombe said] Consider the special case of a circular gravity orbit as viewed from a Cartesian frame. If the centrifugal force ceased, then the gravity force that had been acting as the centripetal force would bring the object straight to the center. A circular motion cannot contain only a centripetal force. It has to have both a centripetal force and a centrifugal force. David Tombe (talk) 09:16, 27 April 2008 (UTC)

[I said] According to the article on force, there are only 4 types of fundamental forces. In the example you just provided, the centripetal force is gravitational. Which type is the centrifugal force?Rracecarr (talk) 13:43, 28 April 2008 (UTC)

RRacecarr, centrifugal force is real whether it is listed in that list of four fundamental forces or not. We are not going to deny the reality of what goes on in a centrifuge because the force in question is not listed on somebody's list of four fundamental forces.

Might you by any chance consider an elliptical orbit as viewed from a cartesian inertial frame. At some stage of the orbit, the gravitational centripetal force is pulling the object closer to the origin. Then there comes a point when the object starts to move radially outwards. Is the force that makes that object move radially outwards on the list of four fundamental forces as per the reference above? David Tombe (talk) 13:58, 28 April 2008 (UTC)

Allow me to insert a few comments here about this entire debate from the viewpoint of Physics as it is used today.

First, viewing things in the cartesian coordinates or radial/tangential components makes no difference - both will have no force acting outward on the mass at the end of a spring (for example). In both frames of reference the centripetal force is supplied by the tension in the string, and the tension is due to the inertia (which is not a force - it is the resistance a body has to change in motion). The more mass the object has, the greater its resistance to a change in motion and the more force will have to be applied toward the center to change that motion.

Viewing the object from a rotating frame of reference will make it appear that there is an outward force acting on the object. This is because the frame of reference itself is accelerating. Accelerations only appear and disappear under coordinate transformations if you are transforming between inertial and non-inertial reference frames. Generally in physics we avoid using non-inertial reference frames for normal motion, like a mass swung at the end of a string or a planet in orbit around a star.

The centrifuge problem is not mysterious. Heavier particles have greater inertia and therefore require a greater force to follow a curved path. The force exerted on lighter particles by the material around it is enough to cause it to follow a curved path. The force exerted by surrounding medium is not great enough to cause the heavier particles to follow a curved path, so they push their way through the medium until the encounter the end of the tube. In either case, the net force acting on the particles is directed inward. Some choose to view this from an accelerating (rotating) frame of reference in which they observe an outward force - and this viewpoint can be useful - but don't confuse the appearance of a force in this frame as a true force, the force arises from the fact that the frame of reference is accelerating.

Which leads me to my last comment - according to how centripetal force is presently taught - it is the net force acting in the radial direction. It is the sum of both inward and outward forces that might be acting on the particle and it is directed inward. For example, if I am sitting in a seat of a car with someone seated next to me, and the car quickly goes through a curve such that I am pushed up against the door of the car, and the other person is pushed up against me, there are two radial forces acting on me. The normal force from the car door is acting toward the center, the contact force between me and the other person is directed out of the circle. The sum of those two forces is the centripetal force. It is just a restatement of Newton's 2nd Law - which in this case the acceleration is centripetal acceleration.

Hope this helps clear things up.PhySusie (talk) 14:45, 28 April 2008 (UTC)

Susie, Thanks for your comments. There are a number of points that you have raised that I would like to go over. You say that in circular motion, there is no outward force even in radial/tangential coordinates?

I would say that there is no net force in the radial direction due to the fact that the centripetal and centrifugal forces cancel out.

In the centrifuge, you say that the net force is inward? Not while the heavy particles are accelerating radially outwards towards the edge.

If heavy particles push past the lighter particles, then we have an effect which is observable from all reference frames. In fact we have a distinct force acting radially outwards.

How can you equate this to the situation in which a stationary object is observed to move in a circle by somebody in a rotating frame of reference? In the latter scenario, there are absolutely no forces acting at all.

Finally, you say that in the Cartesian system, that the centrifugal force does not exist. Inertia is centrifugal force. Centrifugal force acting alone causes straight line motion. If we have a circular motion as viewed in the Cartesian frame, then we have a radially inward centripetal force acting in tandem with inertia.

I do however agree with your assertion that it doesn't matter which kind of coordinate system we use. centrifugal force is either real or it is not real. We therefore may as well use the radial/tangential system for analysis as this is the most convenient.

Anyway, thank you for your comments. David Tombe (talk) 15:05, 28 April 2008 (UTC)

Hi David! It seems like you've retained an intuitive understanding of the term "force" which everyone starts out with, but which is not the same as the physics definition, and which generations of physics teachers have struggled to iron out of people's heads. For example, inertia is not a "force", in the sense that physicists use the term. For example, when a plane travels through the air at constant velocity, Newton's second law says that the net force on it is zero. Have you tried reading about centripetal and centrifugal forces in an intro physics textbook? (Any readable textbook will do.) I think that might help you better understand where PeR, PhySusie, and others are coming from.

Here's an example of your intuitive understanding coming into conflict with the physicists' one. If "there is no net force in the radial direction", then Newton's second law demands that there is no net acceleration in the radial direction (acceleration in the mathematical, not colloquial, sense). And circular motion is impossible without acceleration in the radial direction. See the article uniform circular motion for the relevent formula, for example. :-) --Steve (talk) 17:37, 28 April 2008 (UTC)

Steve, it all comes down to a single question. Are these two situations the same?

(a)An object that is stationary in the inertial frame is seen to move in a circle from a rotating frame. This effect is entirely an artifact.

(b)An object which moves in a circle experiences an outward radial acceleration. The centrifuge is an example of this, and it is a real effect because heavy particles actually partake in relative motion to the lighter particles. As such, there is a real effect which can be observed from all reference frames.

At the moment, the fictitious force page deals with a set of equations which are believed to unite these two effects into one. However, if you look at the derivation of these equations, you will see that the ω for the rotating frame is actually the tangential component of the particle velocity. In other words, the particle velocity is routed through ω.

This physical connection only occurs in scenario (b). In other words, those equations only work when an object is co-rotating.

As it stands now, sceanrio (b) has been removed to another page and explained very badly. It has been explained purely within the context of circular motion in which the centripetal force is being supplied by contact pressure. It ignores elliptical motion and cases that might be caused by tension as in a string, or gravity, electrostatics or electromagnetism.

And the centrifugal force does not alwaays react to the centripetal force. In the case of a tense string, the centripetal force is reacting to the centrifugal force.

I believe that the two articles should be joined together again and that centrifugal force should be introduced as case (b). David Tombe (talk) 07:45, 29 April 2008 (UTC)

David, I know you're interested in arguing whether (a) and (b) are or aren't the same, and are or aren't illusory, but you're destroying your credibility by not using the terms "force" and "acceleration" to mean what they mean in physics. For example, every physics textbook explains why an object which moves in a circle must experience an inward radial acceleration, just the opposite of what you said. It would be worth your while to invest the thirty minutes to read an intro physics textbook on this, so that you can understand what other people are saying and vice-versa. Once you understand what other people mean by "force" and "acceleration", and understand the textbook derivation of centrifugal and coriolis force, and also read up on uniform circular motion, then you'll be in a great position to discuss what is or isn't an illusion or whatever else, without everyone getting hung up and distracted by the technical and terminological errors that you are making. Have you tried this? Do you not have access to an intro physics textbook? --Steve (talk) 16:16, 29 April 2008 (UTC)

Steve, I'm not sure if you have caught on yet to what the argument is about or who is arguing for what. As far as this article is concerned it matters not whether I use the term force or acceleration because we are talking about an inertial force. If I by chance should ever say the word acceleration and you are not happy about it, then just multiply it by mass.

None of this impinges on the issue of what is or isn't an illusion. When heavy particles move past lighter particles in a centrifuge, that is a vision which can be viewed from any frame of reference. Now it's my own opinion that centrifugal force is real and I don't care whether you want to call it centrifugal force or inertia. But that is not what this argument is about. It was last year however. Last year I had a long argument with PeR on whether or not centrifugal force was real, which accounts for his childish behaviour at the moment.

At the moment the issue is quite simply about wording the introduction in the most basic way to describe centrifugal force for what it is. When I looked at the introduction recently, it was in a total mess with some other kind of centrifugal force called 'reactive centrifugal force' being described and described wrongly.

What are the key elements of centrifugal force? It occurs when something moves in a curved path. It doesn't matter whether it is a contact push or a contact pull that causes the direction change. It doesn't matter whether it is gravity, electrostatics, or the Lorentz force. It doesn't matter whether the curve is a circle, an ellipse, a parabola, or a hyperbola. The only point of interest is that there is an outward radial motion in conjunction with tangential motion.

So I have been trying to delete all references to circles, to objects, to reactions, to Netwon's third law etc. because they are all irreleavnt and merely act to cloud the issue.

That is all I have been doing.

The point which seemed to make PeR scream when I first edited the article last week was the reference to the fact that in the days of Newton, Bernoulli, and Maxwell, centrifugal force was considered to be real, but that nowadays the official position is that centrifugal force is fictitious.

PeR being an ardent fictitiousist obviously took great offence at even the mention of the fact that such wasn't always the belief of the ruling physics party.

It's not of course of paramount importance to draw attention to what people believed in the past although there already was a reference to the fact that Newton believed that centrifugal force was real.

The important thing is to give a simple first line description, and mine was modelled on an average of on-line articles on centrifugal force.

I can't think why all this should have caused such a major edit war but it has become quite clear to me that PeR, Henning Makholm, and RRacecarr are determined to promote centrifugal force as a purely fictitious concept and to avoid mention of all such matters as Newton's bucket and the centrifuge etc.

Do the general readers want to see an article beginning with irrelevant stuff about rotating reference frames? You know as well as I do that centrifugal force is frame independent and can easily be described in layman's terms.

Just one after thought. I have read your comments again. PeR may have given you the impression that I hold some kind of unorthodox view on acceleration in circular motion. But my position is quite orthodox. In Cartesian coordinates, a particle has an inward acceleration (the centripetal acceleration) that causes the direction of the particle to continually change but not the speed. PeR was making mischief and engaging in verbal witchcraft because in radial/tangential coordinates, the radial acceleration is zero. (The radial direction itself is of course accelerating). The reason for this was that in the example of the stationary object as observed from the rotating frame, PeR thought that a combined Coriolis force and centrifugal force would yield an inward centripetal force. I pointed out that for circular motion, we need to have the forces in the radial direction balanced. PeR then began to undermine this idea by referring to the Cartesian situation and meanwhle trying to expose an inconsistency in what I had been saying. In fact if you read the dialogue you will notice his style. He often asked questions based on a misrepresentation of what I had said before.

So forget about all that about centripetal force and meanings of acceleration or force. The main issue is about getting a simple description of centrifugal force into the introduction. David Tombe (talk) 18:44, 29 April 2008 (UTC)

Again, David, every post you write has physical and mathematical errors (or at best, "unconventional terminologies") that are distracting from what you're trying to say and harm your credibility. For example, there's a well-defined, coordinate-independent thing called acceleration. The acceleration of a circularly-rotating object points radially inward in any system of coordinates, not just cartesian. The way everyone else understands the term "radial acceleration" is the component of acceleration in the radial direction. You, apparently, sometimes mean that, and sometimes mean "second derivative of the radial coordinate in polar coordinates". So if that's what you mean, say "second derivative of the radial coordinate in polar coordinates". Then everyone will understand what your saying. Likewise, force is equal to mass times acceleration, but "radial force" (meaning the radial component of force) is not equal to "mass times the second derivative of the radial coordinate in polar coordinates". If you want to discuss "mass times the second derivative of the radial coordinate in polar coordinates", that's fine, just call it by that name, not by the term "radial force" or "force in the radial direction", since no one else would call it by that name.

Have you found and read a textbook on this yet? I imagine you could have done so many times over in the time it took you to compose that response. :-) --Steve (talk) 18:07, 30 April 2008 (UTC)

Steve, This is nothing to do with unconventional terminologies. But just for the record, I have always been referring to the total acceleration in the radial direction. I have not been restricting my meaning to the r double dot term. In circular motion the sum of r double dot and r theta dot squared is zero.

But anyhow, shall we get to the main point. My proposed introduction today was erased because it contained an unacceptable truth. It contained references to true situations which might cause a reader to question whether or not 'fictitious' was the best term to use to describe centrifugal force.

In the wake of the reversion, a new character arrived on the scenes by the name of Anome. He immediately started to pile on references to back up the fact that there are sources which say that centrifugal force is fictitious.

We all know that.

But that doesn't mean that we have to hide away other true facts that might cause people to question the term. Those true facts are (i)In cases of co-rotation, a particle experiences an actual acceleration in the outward radial direction, and (ii) that in a rotating bucket of water, a hydrostatic pressure is induced.

There is no original research there. There is no point of view being expressed. And there is no need for references for such basic facts.

But these facts are not being tolerated and they are being hastily erased.

Just to prove that what I am saying is right, can you answer me one question. Would you support an introduction that highlighted the term 'fictitious' with loads of citations, but then went on to mention things which might pour some doubt on the suitability of the term? And by those things, I'm talking for example about the centrifuge and the hydrostatic pressure in the rotating bucket.

And I don't really believe at all that you can't see through all this, and what exactly is going on. You are pretty smart. You are smarter than most, but sometimes you get blinkered by terminologies and lose sight of the higher picture.

This is not about terminologies. This is about denial. This is about refusal to see a mechanical equivalent to the Faraday paradox.

By the way, I'm always amused about these beginners physics books that you want me to look at. What level do you have in mind? David Tombe (talk) 12:59, 1 May 2008 (UTC)

I have no idea what your education, background, or position is. But whatever it is, your statement: "in circular motion...there is no net force in the radial direction" is false. In circular motion, there is a net force, and it's radially inward, as is clearly explained in every introductory college-level physics textbook. If you're a professional physicist, then you are a professional physicist who would benefit greatly from carefully re-reading the appropriate section of an introductory college-level physics textbook. If you've never read an introductory college-level physics textbook, you really should, and in fact you probably should have done that before accusing everyone else of being confused and reverting their edits. You keep trying to change the subject, but I'm going to keep telling you that until you stop repeatedly making elementary factual errors such as this one, no one will believe that you understand what you're talking about. --Steve (talk) 16:06, 1 May 2008 (UTC)

Steve, there can be no reason to ever justify dealing with circular or elliptical motion problems in Cartesian coordinates. It is like trying to fit a square peg into a round hole. We always end up talking about the radial direction no matter how hard we try not to. The only people who want to introduce Cartesian coordinates into circular motion are those who want to confuse the issue in order to detract attention away from the failure of their own theories in polar coordinates.

All these matters and arguments can be dealt with satisfactorily entirely within the language of polar coordinates. And in polar coordinates, when a body is moving in a circle, the net radial acceleration is zero.David Tombe (talk) 10:25, 2 May 2008 (UTC)

David, when you say polar coordinates, do you mean polar coordinates for an inertial, stationary frame or polar coordinates for a rotating frame? Or do you not distinguish between the two? --FyzixFighter (talk) 15:52, 2 May 2008 (UTC)

David, I'll respond assuming you meant in the inertial frame, since that appears from context to be what you're saying. The acceleration of a rotating object is radially inward in any system of coordinates for the inertial frame. Here's polar, for example: The expression for outward radial acceleration is (r double dot - r (theta dot)^2). r isn't changing, so r-double-dot is zero. Theta is changing, with theta-dot = v/r. So you get (0-r(v/r)^2)=-v^2/r acceleration in the outward radial direction, which corresponds to +v^2/r acceleration in the inward radial direction. Exactly the same result as you can derive with cartesian coordinates, or with any stationary coordinate system, or with no coordinate system at all! (See the article uniform circular motion for a coordinate-independent derivation.) If you don't understand this, I promise that you'll find a clear explanation in an intro college-level physics textbook. Please do this simple step now, not later. --Steve (talk) 16:32, 2 May 2008 (UTC)

David: You might look at circular motion example. In that example the mere fact that a particle moves in a circle is shown to imply an inward acceleration radially toward the center of the circle. Newton's second law then says there is a force ( m × a ) at work to keep the motion in a circle. Maybe it is apocryphal, but story is that Newton asked why the moon did not fall to the earth, since it is attracted by gravity. His answer: the moon does fall toward the earth, but it also is moving tangentially so rapidly that the little progress it makes in dropping toward the earth is made up for by the tangential movement that carries it further away. Gravity provides the centripetal force needed to keep circular motion. Brews ohare (talk) 17:52, 2 May 2008 (UTC)

Brews, Exactly. From a Cartesian perspective. But as soon as you start to talk the language of 'radial', then a centripetal force is balanced by a centrifugal force. This conversation is continued in a special section at the bottom of the page. David Tombe (talk) 17:57, 2 May 2008 (UTC)

Come on, David. You aren't really going to argue that the physical prediction of the need for a centripetal force will be different if I change variables? What kind of physical theory depends upon the coordinate system? It's just a mathematical convenience! If you need convincing, circular motion example is almost in circular coordinates already: just do it. Brews ohare (talk) 18:17, 2 May 2008 (UTC)

Brews, Correct. The physics doesn't change simply by changing coordinate frames. But we use polar coordinates for these issues because they give us a radial direction. There is no other way to conceive of the direction of centripetal force. And as soon as we start thinking 'radial' for centripetal force, then there will be a radial centrifugal force too.

In the Cartesian frame we are dealing with exactly the same physics. But it is much more complicated to express. It involves the angular rotation of that radial vector (which is where your actual acceleration comes into it) in conjunction with 'inertia'.David Tombe (talk) 18:47, 2 May 2008 (UTC)

Hi David: I posted a coordinate system free, entirely vector derivation at Vector derivation. I obtain the same answers. There is only the centripetal force. Does that settle things? Brews ohare (talk) 21:28, 2 May 2008 (UTC)

Comments on the Split

What appears to have happened now is that the ultra fictitious case of centrifugal force, which is based on a faulty interpretation of maths, has been moved to a position of primacy in an article all of its own, as being the flagship carrier for centrifugal force. It seems that the editors think that this is what the public are looking for when they go to look up centrifugal force.

Centrifugal force is no loner the real effect that occurs in the centrifuge. It is now a fictitious circular motion that we observe from a rotating frame of reference.

Well as far as that is current textbook theory, then the introduction is basically correct now since I have removed the bit about the object having to be moving. If we're going to have a wrong article, better that it is correctly wrong.

Unfortunately though, real centrifugal force has been moved away to a page of its own where people are less likely to look. And it has been totally confused by giving it the misnomer 'Reactive centrifugal Force'. Yet we can see clearly in the case of a weight being swung around on the end of the string that centrifugal force is anything but reactive. And more so in the centrifuge where the heavier particles push their way through the lighter particles to make their way to the outer edge. What is that supposed to be in reaction to? Certainly not the centripetal force as is claimed in the article.

Then to make matters worse, the article gives the impression that centrifugal force is only something that occurs with circular motion, and not elliptical or hyperbolic motion. It would seem that the latter two concepts were too advanced for whoever wrote the article.

And finally, whoever wrote the article considers contact pressure with an object to be the only legitimate means of bringing about centrifugal force. Gravity, electrostatics, and the Lorentz force have been excluded.

All attempts to generalize it to curved motion caused by any force have been fiercely resisted particularly by PeR and FyzixFighter.

Clearly there is team vandalism going on at present on this article. It is now in a worse state than when the edit war began. David Tombe (talk) 07:57, 28 April 2008 (UTC)

Reply to PeR

PeR, there is no need to leave formal warnings for me in my tray. You have accused me of wikistalking. That is very rich coming from you. It's a case of the pot calling the kettle black.

You and FyzixFighter have been actively making a point of deleteing every single edit that I make. I am trying to improve this article. I tried to generalize the definition of centrifugal force but both of you reverted it to a high school version that shies away from anything more complicated than a circle.

That is wikistalking if ever there was a case. You are simply making that statement that you will let Wolfkeeper and Rracecarr edit these pages but under no account are you going to alow me to have the slightest input. That is wikistalking.

So do you want to call a truce, or do you want the administration to be brought in? David Tombe (talk) 08:04, 28 April 2008 (UTC)

The vandalism warning concerned your edit to Rollerblade. It has nothing to do with this article. If you want to discuss the edit, then do so on Talk:Rollerblade. If you want to discuss the warning, then do so on your talk page. --PeR (talk) 08:27, 28 April 2008 (UTC)

And likewise, do you want to discuss why you removed my edits yesterday? I generalized circular to curved. I generalized contact pressure forces to all forces. And I pointed out that centrifugal force is not reactive, but rather centripetal force is reactive. But you and FyzixFighgher swiftly reverted those edits as a matter of duty to your team. That is foul play. You can't have it both ways. If you are going to delete all my edits, then you are going to see all your edits deleted too. And if the administration come in then its all your fault. David Tombe (talk) 10:30, 28 April 2008 (UTC)

Space elevator

OK, here's a reasonably good example of centrifugal force. In the rotating frame of reference that is rotating with the Earth- centrifugal force holds up the space elevator. While in the inertial frame of reference it's (ironically) inertia, in the Earth-synchronous rotating frame of reference- it isn't moving. The force that holds it up is the centrifugal force.- (User) WolfKeeper (Talk) 08:25, 28 April 2008 (UTC)

Wolfkeeper, I can simplify that for you.

In the Inertial frame of reference, it is inertia that holds the space station up.

In the frame that is co-rotating with the space station, you can use those equations for the rotating reference frame BECAUSE the object in question is co-rotating. And so, yes, it is centrifugal force that holds the space station up in the rotating frame.

Ah hah! Doing that, that is what this article is about.- (User) WolfKeeper (Talk) 10:43, 28 April 2008 (UTC)

Except these equations in the article deal with the general case, where the elevator is wobbling around, and not totally stationary, and there are elevator cars generating coriolis forces on the cable as they climb it, and with the moon pulling this way and that way, and with the Earth attachment point being moved around by ship- all this can be done in the rotating frame of reference.- (User) WolfKeeper (Talk) 10:45, 28 April 2008 (UTC)

Either way, the effect is observed from both reference frames whether you call it centrifugal force or inertia.

But this is not the same as the artificial circle scenario in which the object is at rest in the inertial frame. In that case, you cannot apply those equations. There is no co-rotation and there is neither inertia nor centrifugal force.

In my books, inertia is merely centrifugal force as observed in an inertial frame of reference.

Let's not lose track of the main point of the argument. The centrifuge effect is viewable from all frames of reference. It causes heavy particles to have relative motion to lighter particles. But that effect only occurs when the object co-rotates with the rotating frame. It doesn't matter whether we chose to call it inertia or centrifugal force.

So why not simplify the article and leave rotating reference frames out of it. Why not describe centrifugal force in its simplest manner ie. the outward radial force that occurs on all objects that are constrained to follow a curved path.David Tombe (talk) 10:26, 28 April 2008 (UTC)

Because it would totally piss-off (among others) weathermen, who spend all their working life working in a rotating reference frame, without ever wishing to do all their work in a non rotating reference frame?- (User) WolfKeeper (Talk) 10:39, 28 April 2008 (UTC)

Wolfkeeper, the equations are fine so long as the object in question co-rotates. When the object co-rotates, we have centrifugal force. When the object doesn't co-rotate, we have nothing.

Are you incapable of seeing the difference between an illusion of circular motion and a very real radial force that can cause hydrostatic pressure?David Tombe (talk) 14:03, 28 April 2008 (UTC)

Sorry, David but your assertion is wrong. Any object in rotating reference frame will experience a centrifugal force (and a coriolis force). It is just that when it is co-rotating with the frame (i.e. it is stationary in the rotating frame) it feels only the centrifugal force and no coriolis forces, because those happen to be zero. For a noninteracting object, the coriolis and centrifugal forces will conspire tot let the object follow the straight path it would follow in the inertial frame. Very simple. (TimothyRias (talk) 11:35, 29 April 2008 (UTC))

Timothy, you are overlooking quite a number of factors. In one scenario, there is a very real effect. It can cause hydrostatic pressure in a liquid. It can cause heavy particles to push past light particles in a way that can be viewed from all reference frames.

In the other sceanrio, nothing happens. All we get is the illusion of a circular path as viewed from the rotating frame.

You seem to think that these two effects are exactly the same and that they are united under the maths for rotating reference frames. In fact, that maths only applies to the former scenario. If you see the derivation of that maths you will notice that the ω term which is ostensibly the angular velocity of the rotating frame, is actually physically related to the tangential component of the moving particle.

If the particle does not co-rotate, then you can't apply those equations.

The derivation, for the same resons also tells us that the v term for the rotating frame has to be radial. Centrifugal force is a radial effect arising from a tangential motion, and the Coriolis force is a tangential effect arising from a radial motion. In fact from the velocity formula you can actually see that they are two mutually perpendicular aspects of the same thing.

Hence, there will be no Coriolis force ever acting in the radial direction.

So your argument about the stationary particle experiencing a centripetal force composed of an outward centrifugal force added to an inward Coriolis force that is twice as strong, is wrong.

And it is further wrong on the grounds that it would lead to a net inward radial acceleration. In circular motion, we need a net zero radial acceleration.David Tombe (talk) 12:16, 29 April 2008 (UTC)

First of all the effect is real in both cases. In the sense that a particle that is stationary in an inertial frame, really moves in a circle in the rotating frame. This is not an illusion. The physics in the rotating frame is just as good as in the inertial frame. It depends on the physical situation which happens to be easier to use.

Your statement If you see the derivation of that maths you will notice that the ω term which is ostensibly the angular velocity of the rotating frame, is actually physically related to the tangential component of the moving particle. is false. In the formula:

$\mathbf {a} _{\mathrm {rot} }=\mathbf {a} -2\mathbf {\omega \times v} -\mathbf {\omega \times (\omega \times r)}$

ω is the angular velocity of the frame and nothing else. Only the variable r and v (the later being the time derivative of the first) have any relation to the particle. If a particle is stationary in an inertial frame, then ofcourse v is related to ω through $v=-\omega \times r)$. In that case the coriolis acceleration is $-2\mathbf {\omega \times v} =2\mathbf {\omega \times \omega \times r}$ which is twice the centrifugal acceleration but pointed inward. Thus refutes your statement that Hence, there will be no Coriolis force ever acting in the radial direction.

Finally we have your statement In circular motion, we need a net zero radial acceleration. which is just plain wrong. Circular motion just as any other nonstraight motion implies a netto acceleration, because obviously the velocity is not constant. (it changes direction). This is basic high school physics. (TimothyRias (talk) 12:57, 29 April 2008 (UTC))

Timothy, I have already considered all your points many times. If you look at the derivation of the formula above, you will see that v is routed through ω. They are not independent of each other. In the limit for calculus purposes v reduces to exactly the radial velocity, and ω will always implicitly contain the tangential velocity. There is no point in reading the final result out to me. I studied it all years ago.

The application of this formula which you are making is detached from the physical reality upon which the formula was derived.

And on your other points, there will indeed be an inward acceleration in a circle when we look at it in Cartesian coordinates. This inward acceleration changes the direction of the particle but not its speed. However, if we move over to radial/tangential coordinates, then the radial force will be zero. In your example, which is done in radial/tangential coordinates, the net radial acceleration is not zero and so it doesn't describe a circle. David Tombe (talk) 18:09, 29 April 2008 (UTC)

Do you have a reference for that bizarre claim? You keep saying that, but it isn't true. If it was true, merely changing from cartesian coordinates to polar coordinates would make something go around in a circle all by itself!!!!!- (User) WolfKeeper (Talk) 19:39, 29 April 2008 (UTC)

Wolfkeeper, now you are starting to talk nonsense. How do you infer that the inapllicability of a set of equations means that changing between two coordinate systems would make something go around in a circle all by itself!!!!!? You have now ceased to engage in rational argument. You are at that stage where you misrepresent and twist what others have said and then ridicule your own misrepresentations.David Tombe (talk) 20:11, 29 April 2008 (UTC)

I'm sorry if you think that that is the case, I would never do that intentionally. However, I'm hoping that you will be able to cite this claim of yours, because I don't see how this could ever be, but since it's true, you'll be able to give us a good reference?- (User) WolfKeeper (Talk) 22:12, 29 April 2008 (UTC)

You have been over extending the application of a formula which was derived exclusively to cater for particles in co-rotation, or to put it more simply, to cater for particles which are actually moving in a circle.

On your other point, I'm not going to get into an argument about whether or not both situations are real. I would just hope that you would realize that the two situations are quite different. In one situation, an object sits still and nothing happens to it. In the other situation, there is an actual tangential motion which leads to a radially outward motion which can cause pressure and diffusion that is visible from all frames of reference. check out the Bucket argument. David Tombe (talk) 18:09, 29 April 2008 (UTC)

David, would you mind explaining why you keep claiming that ω has anything to do with the velocity of the particle. There are plenty of ways to derive the above result that clearly show that this is not the case. ω is nothing more than a parameter in coordinate change $\mathbf {x} \rightarrow R(\mathbf {\omega } t)\mathbf {x}$ where R(ω) is a rotation matrix. If $\mathbf {r} (t)$ is a path then $\mathbf {r} (t)\rightarrow r_{rot}(t)=R(\mathbf {\omega } t)\mathbf {r} (t)$ and for the second time derivative ${\ddot {\mathbf {r} }}_{rot}(t)\rightarrow {\ddot {\mathbf {r} }}(t)-2\mathbf {\omega \times {\dot {r}}_{rot}(t)} -\mathbf {\omega \times (\omega \times r_{rot}(t))}$. Which is the result above. Omega in no way depends on r. (TimothyRias (talk) 07:50, 30 April 2008 (UTC))

Requested move

The following is a closed discussion of the proposal. Please do not modify it. Subsequent comments should be made in a new section on the talk page. No further edits should be made to this section.

The result of the proposal was move. 199.125.109.99 (talk) 17:14, 1 May 2008 (UTC)

• Centrifugal force (fictitious) → Centrifugal force —(Discuss)— Moved a few days ago with no real consensus. This force is always called centrifugal force; that it is 'fictitious' does not need to be part of the title. The way, the truth, and the light (talk) 17:32, 28 April 2008 (UTC)

Just to be clear, you're proposing that we keep the article reactive centrifugal force the same, but move centrifugal force (fictitious) to centrifugal force, right? To me, it comes down to: When the term "centrifugal force" is used in a physics (or non-physics) book or paper, what percentage of the time is it referring to the fictitious one and what percentage is it the reactive one? If it's always, or almost always, the fictitious one, then I'd definitely support that move. If it's 50-50 or thereabouts, a straight-up disambiguation page (as now) would presumably be more appropriate, following WP:NPOV. Can anyone find prominant real-world examples where the term "centrifugal force" is used for the reactive one? Certainly the fictitious one is quite prevalent in textbooks. :-) --Steve (talk) 18:03, 28 April 2008 (UTC)

When I did the search for any reactive force mentions, I found few, but some of the ones were fairly significant (principia). However the most frequent use of the term 'centrifugal force' probably refers to the incorrect force that 'exists' in a non rotating reference frame which is purely inertia. I added that to the disamb page, but it got delete.- (User) WolfKeeper (Talk) 02:33, 29 April 2008 (UTC)

Frankly, I'd like to see the articles recombined into one, with a clear distinction between what is fictitious and what is not. The present duo look together like a POV split, even if they aren't. Mangoe (talk) 20:35, 28 April 2008 (UTC)

I don't think it's going to happen, the policy is that wikipedia is not a dictionary, and we don't have articles that cover two or more different topics just because they share an article name.- (User) WolfKeeper (Talk) 02:33, 29 April 2008 (UTC)

Well, the problem is that in a sense they aren't "different", in the sense that they both "occur" in the same context. If this article is kept separate, then centrifugal force becomes a disambig-- except that to make that work, you'll have write a disambig that explains the difference, in which case there's no need for three articles. I really don't think there's a coherent way to explain one without having to explain the other. Mangoe (talk) 03:30, 29 April 2008 (UTC)

I guess I'm imagining that they'd be kept separate, this article would be renamed "centrifugal force", and it would start with This article is about centrifugal force, a fictitious force in physics. For the real outward-acting force that exists in all circular motion see Reactive centrifugal force, or something like that. The misuse as "inertia" is certainly a bona fide third definition, but I think it fits well enough to be included in the main (fictitious force) article. Combining everything back into one article is another legit possibility, but the current overlap in content isn't overwhelming, and moreover I think it's nice to tuck away the less-common and less-important concept so that it won't bother and distract the average reader. :-) --Steve (talk) 04:29, 29 April 2008 (UTC)

No, they apply in different contexts. Centrifugal force can be applied when nothing physically is rotating at all. Reactive centrifugal force only ever occurs when something is rotating. They can occur together or separately. You can have multiple examples of reactive centrifugal forces occuring simultaneously with different centers while a pseudo centrifugal force can only have one center at a time. They are completely and utterly distinct concepts.- (User) WolfKeeper (Talk) 04:55, 29 April 2008 (UTC)

Wolfkeeper, you are wrong. See my reply to Steve above. When nothing is physically rotating there can be no centrifugal force. I think that your belief to the contrary lies at the root of this problem. You are backed up by superior numbers, but I believe that you are wrong.

Well, I know I'm correct, because I've read lots of web pages on it, I was taught it at degree level, and I've even simulated it on a computer. I know it backwards, forwards and inside out. And that's how I know you're completely wrong. Sorry.- (User) WolfKeeper (Talk) 08:09, 29 April 2008 (UTC)

Yesterday, I drew your attention to the fact that the ω of the rotating frame of reference has to also be physically connected to the tangential speed of the particle. If the particle is sitting still in an inertial frame, then there is nothing doing. The situation is quite different from the situation which occurs in a centrifuge.

No, the frame of reference can do whatever the hell it wants, it can spin the opposite way if it wants, or not spin at all (w=0). You normally would make the frame of reference rotate the same as a particular physical object, but you absolutely don't have to, and everything works- you can run the maths in the rotating reference frame and then after that transform it all back to the inertial reference frame using a rotation operator and everything is precisely in the right place.- (User) WolfKeeper (Talk) 08:09, 29 April 2008 (UTC)

This analogy extends to Coriolis force. If a bird flies over a rotating children's roundabout, then the Coriolis force is entirely fictitious. There is no physical connection between the two situations.

What would happen if the child grabbed the leg of the bird as it flew past? The Coriolis force would still act. It's not completely fictitious. I actually prefer the term 'pseudo' force, because that makes clear it's not a real force, but it is real, it is real inertia. Fictitious implies that it is completely illusory, but that isn't so.- (User) WolfKeeper (Talk) 08:09, 29 April 2008 (UTC)

But in cyclones in the atmosphere, the moving elements of air are physically connected to the larger entrained body of atmosphere. Hence the effects can be real, as like in the centrifuge. I have been trying to impress this point on Rracecarr but without any success. David Tombe (talk) 07:52, 29 April 2008 (UTC)

Centrifugal and coriolis pseudo forces are certainly real. They can kill you(!) If it can kill you it is real. It is really inertia that only appears to be a force due to the coordinate transformation that you do to get to the rotating reference frame.- (User) WolfKeeper (Talk) 08:09, 29 April 2008 (UTC)

Yes, Wolkeeper, inertia is real. But that is not the argument. The argument is about distinguishing between cases in which the effects are purely fictitious and cases in which the effects are real. David Tombe (talk) 08:29, 29 April 2008 (UTC)

They're always real pseudoforces. They are not truly fictitious. Fictitious implies that they're completely and utterly made up, like Sherlock Holmes- he never existed. But no, fictitious forces are not like that. Inertia is real and can kill you. Pseudoforces are inertia and are real and can kill you.- (User) WolfKeeper (Talk) 08:37, 29 April 2008 (UTC)

Wolfkeeper, you still don't understand the difference between the real effect which occurs during actual curved path motion, and the fictitious effect which is observed when a stationary particle is observed from a rotating frame of reference. David Tombe (talk) 12:18, 29 April 2008 (UTC)

Merge the two articles. There is no good reason to split in two articles; they are about the same effect in different situations. (TimothyRias (talk) 11:41, 29 April 2008 (UTC))

• The readers coming in from search-engines and internal wikilinks are best served by a common article at centrifugal force that explains the topic in its entirety. We cannot in this case expect a layman to pick his way through a inadequately-lengthed "discussion" at a disambiguation page to decide for himself which page he needs; give him all the relevant information where he expects it to be at a central article. Support a move back to the status quo ante. Knepflerle (talk) 13:28, 29 April 2008 (UTC)

• Support move and remerger - this whole issue is one long confusion of terms that only arises when using filthy imprecise words instead of the beauty of abstract mathematics. - Eldereft ~(s)talk~ 16:59, 29 April 2008 (UTC)

• Support move and remerger - while I understand the good faith intentions of the original split, the references to a "reactive centrifugal force" are few and far between. Also, in some cases there is no reactive centrifugal force, such as in planetary orbits where the action-reaction pair of forces are both centripetal. --FyzixFighter (talk) 17:29, 29 April 2008 (UTC)

• Compromise proposal: This article is renamed "centrifugal force", and its scope broadened to include everything called centrifugal force. But, it includes only a short section on the "reactive centrifugal force", which says Main article: Reactive centrifugal force. It's a win-win, one article on everything, but some not-especially-important concepts and details are sequestered into their own article. Eh? --Steve (talk) 00:29, 30 April 2008 (UTC)

The two should not be merged just because they have the same name. They're completely different, apply to different situations, are likely to be of interest to different audiences, were invented hundreds of years apart; and the wikipedia is not a dictionary. Dictionaries have an entry per name. Wikipedia has an article per topic. These are different topics.- (User) WolfKeeper (Talk) 02:52, 30 April 2008 (UTC)

You might want to reread the compromise, Wolfkeeper, Steve's compromise still maintains two articles, and (if I understand it correctly) is in fact somewhat similar to the current situation. The compromise would require trimming the "reactive" article a bit to have only the barest mention of the pseudoforce, and placing a brief summary section and Main article: link to the "reactive" page here as well as renaming this article to simply "centrifugal force". The only thing lost is the disambiguation page, but the compromise appears to be more like how spin-off articles are handled. Steve, correct me if I haven't understood your compromise properly. Thoughts on this arrangement? --FyzixFighter (talk) 04:24, 30 April 2008 (UTC)

That's right, I'm proposing two articles: One main, general one, which only briefly mentions the reactive force as a rare alternative definition, and one spin-off article, which is only about the reactive force. --Steve (talk) 17:49, 30 April 2008 (UTC)

I think that's what we have right now really; I've turned the disamb into a redirect to Centrifugal force (fictitious), and I've moved the discussion about the differences into the reactive article. Still, I don't completely agree with this layout, I think that the centrifugal force article is better as a disamb because the disamb is understandable by everyone, whereas the centrifugal pseudoforce is really an advanced topic, and we're kinda dumping everyone searching for 'centrifugal force' into it, where they will probably get confused, but that really is what people mean by 'centrifugal force' in the main so according to policy it should go there, or a disamb. But I just don't see the disamb page structure surviving 'a thousand wiki editors' as it were, I think this structure should be more stable. Stability is good.- (User) WolfKeeper (Talk) 03:07, 1 May 2008 (UTC)

The above discussion is preserved as an archive of the proposal. Please do not modify it. Subsequent comments should be made in a new section on this talk page. No further edits should be made to this section.

More on pseudo forces and merges

But there's no pseudo force in that situation either, so I'm not certain what your point is really.- (User) WolfKeeper (Talk) 17:37, 29 April 2008 (UTC)

And there's really 3 different meanings of the phrase, reactive, pseudo, everyday.- (User) WolfKeeper (Talk) 17:37, 29 April 2008 (UTC)

Wolfkeeper, there is only one centrifugal force. The reactive thing is a knock on effect in a collision. All you need to do is describe what centrifugal force is in simple terms and leave the readers to make up their own minds as to whether it is real or not. My opinion is that it is real because the centrifuge effect can be observed from every frame of reference.

Rotating frames of reference only cloud the issue. David Tombe (talk) 17:56, 29 April 2008 (UTC)

Coriolis effect comes out of the same equation as the centrifugal effect. Are you seriously saying that that doesn't exist either? Better tell those cyclones and anticyclones to stop spinning. "Stop! Stop I say, David says you don't exist! Stop!"- (User) WolfKeeper (Talk) 18:28, 29 April 2008 (UTC)

Wolfkeeper,That was a complete misrepresentation of everything I have been saying. I am the one that has been saying that the effect in the atmosphere is real. The others, such as Rracecarr are the ones that have been saying that it is purely fictitious. You have been sitting on the fence saying that it is not quite fictitious. David Tombe (talk) 20:07, 29 April 2008 (UTC)

David, we are describing the centrifugal force as it is described in reliable sources. And in these reliable sources, the centrifugal force and the Coriolis force are pseudo-forces, artifacts of inertia when describing motion in rotating frames. We do not have to convince you that you are wrong, or that your understanding of physics is incorrect. Nor do you have to convince us that we are wrong. The other editors have shown great patience in trying to explain the physics, but at the end of the day it doesn't matter whether you believe it or not. Wikipedia is based on reliable sources and verifiability, and all sources support the rotating frame, pseudo-force view of the centrifugal force. So either provide a reliable source for the statement that inertia is a force and that the centrifugal force is real and not pseudo, or it doesn't go in. Simple as that. --FyzixFighter (talk) 19:37, 29 April 2008 (UTC)

FyzixFighter, There is nothing in any of my edits which you have deleted that either criticizes the orthodox position on rotating coordinate frames or make the claim that centrifugal force is real.

You have been deleting edits which describe in simple terms exactly what centrifugal force is. It is an outward radial acceleration which occurs when an object moves in a curved path. David Tombe (talk) 20:15, 29 April 2008 (UTC)

Source, please? --FyzixFighter (talk) 20:17, 29 April 2008 (UTC)

No FyzixFighter, I won't give you a source for that fundamental fact. Children learned it in the garden when they swung a bucket of water over their heads. You have simply shown yourself up here as nothing but a trouble maker. You have stormed in on a wikistalking mission and then decided to go and make accusations against me when I hit back. You are just a trouble maker. You are not here to improve the article at all. David Tombe (talk) 20:46, 29 April 2008 (UTC)

From "Analytical Mechanics", Hand & Finch, pg 267 (1998) - "The last three terms on the right hand side above [the centrifugal force, the Coriolis force, and the Euler force] aren't real forces; they are purely kinematic consequences of the rotation of the body coordinates." --FyzixFighter (talk) 21:46, 29 April 2008 (UTC)

Merge the Articles

Wolfkeeper, you should merge the articles. Reactive centrifugal force is a knock on effect which occurs when something that is experiencing centrifugal force knocks against something else. It is not even covered in this article because you have turned cause and effect upside down. and it doesn't really need to be covered at all unless you might wish to write a section on it.

There is only one centrifugal force but there is an argument about whether it is real or fictitious.David Tombe (talk) 12:35, 29 April 2008 (UTC)

David is correct, there is no fictious centrifugal force and your attempt to invent one to satisfy your confused notions of physics is just a fiction itself. 72.64.49.249 (talk) 13:20, 29 April 2008 (UTC)

Leave things as they are: it is clear and clean. Brews ohare (talk) 14:55, 3 May 2008 (UTC)

The Faraday Paradox and the Bucket argument

When a bucket of water is swung in circular motion, it induces a hydrostatic pressure in the water. That is an effect which is observed from all reference frames. It is absolute. It is quite wrong to state that centrifugal force is an effect which is only observed in rotating frames of reference.

The closest that you could get to making that statement true would be to say that this effect is called 'centrifugal force' when it is observed from a rotating frame of reference but when it is observed from an inertial frame, the modern tendency is to refer to this effect as having been caused by inertia.

This effect, whether we call it centrifugal force or inertia, is not the same as the situation which we are dealing with when we observe a stationary object from a rotating frame. In the latter case, there is no real effect. These two circular motion situations are every bit as different from each other as two important circular motions in electromagnetism that are connected with the Faraday paradox. When we move a charged particle tangentially in the equatorial plane of a magnetic field, we get an induced electromotive force. But when we rotate the magnet on its magnetic axis with the particle stationary, we only get the artificial circle as observed from the frame of the rotating magnet. Nobody has ever said that these two effects are the same. Likewise in mechanics. There are two different effects and only one of these effects is centrifugal force.

Hence, there should be one single article on centrifugal force. Reactive centrifugal force does not need to be mentioned as it is merely a knock on effect in collisions and contact pressure situations. It can however be mentioned in a section, if somebody so wishes it to be. But I hope they manage to get the action and reaction the right way around.

Now moving on to the maths. If you look at the derivation of the rotating frame equations, you will see that ω which refers to the angular velocity of the rotating frame also refers to the angular velocity of the particle. It is a simple vector triangle. The particle velocity is split into two components. In the limit, this becomes a tangential component connected with ω, and a radial component which comes into play for Coriolis purposes.

That's quite simply wrong. If you believe that, then I want you to point to the equation where that is assumed in a reliable reference source. All the derivations I have seen make no such assumption.- (User) WolfKeeper (Talk) 02:49, 1 May 2008 (UTC)

Hence, these equations only apply to co-rotation, and to real Coriolis force when the radial velocity is physically referenced to the rotating frame such as in the hydrodynamics of the atmosphere, which of course is why the cyclones are real and not merely apparent.

So how should we proceed with a wording which does not conflict with the textbooks?

Centrifugal force is a term used within a rotating frame of reference, and it applies to the outward radial force which acts on objects which are stationary within the rotating frame. This effect can be extended to all curved path motion.

In the inertial frame of reference, this effect is said to be caused by inertia. David Tombe (talk) 09:23, 30 April 2008 (UTC)

The Three aspects of the subject matter

Steve, you mention about a spin off article for reactive centrifugal force. Do you mean another page? Can it not be handled as a section near the end of a united centrifugal force article?

The so-called reactive centrifugal force seems to have caused the editors to overlook a more fundamental division of effects within what modern textbooks call centrifugal force. This division splits along similar lines as in the Faraday paradox.

There is a real effect which occurs in a centrifuge. That is a radial outward pressure associated with actual curved path motion.

There is a fictitious effect which is associated with a stationary object being viewed from a rotating frame.

Personally, I would only use the term centrifugal force to cover for the real effect. But if the textbooks blend the two together under one set of umbrella maths, then we need to specify these two scenarios as per the Bucket argument. We cannot overlook the physical difference on the ostensible grounds of a unifying maths. That would be like overlooking the difference between the time dependent aspect of the Lorentz force and the motion dependent aspect on the grounds that one single equation covers them all.

We must specify the hydrostatic pressure in the rotating bucket as one scenario, and the stars rotating across the sky as another scenario.

We can have an introduction which sticks to textbook terminologies. But we cannot make the blanket assertion that centrifugal force is fictitious. It is sometimes fictitious and sometimes real.

Editors here have devolved all the real stuff to 'reactive centrifugal force' and deemed the rest to be fictitious. That is not a correct division. There is real centrifugal force before any reactions occur at centrifuge walls.David Tombe (talk) 18:16, 30 April 2008 (UTC)

Reply to Wolfkeeper

Wolfkeeper, If you had read the new introduction, you would have seen that it unequivocally maintained the position that the centrifugal force applies to all objects. I disagree with that, but that is the official position.

You reverted me on the false grounds that I had alleged otherwise.

I haven't got a citation that would explicitly state that the coordinate transformation equations only apply to co-rotation. I can see it just by looking at the vector triangle in the derivation. The particle velocity is split into two components. The tangential velocity of the rotating frame becomes one of those components. Hence the two things are physically linked.

That's WP:Original Research. Go away and get a proper citation, and we'll add it to the article.- (User) WolfKeeper (Talk) 18:36, 1 May 2008 (UTC)

The introduction which I have put in now was carefully thought out to cover all aspects of the controversy.

Read it and think about it before you revert it. David Tombe (talk) 06:19, 1 May 2008 (UTC)

revert

"To the extent to which the object or fluid element co-rotates with the frame, a radial acceleration or a hydrostatic pressure is induced."

A radial acceleration is always induced everywhere in the rotating frame proportional to distance from the axis. It may or may not be balanced or enhanced by other (pseudo)forces, but it's not a matter of the extent of corotation.- (User) WolfKeeper (Talk) 06:21, 1 May 2008 (UTC)

No Wolfkeeper. A radial acceleration only occurs in co-rotation situations as does hydrostatic pressure. I know exactly what you are thinking, and I deliberately worded it to avoid that controversy.

Let's just say for the sake of argument that those equations do actually apply to all situations. Whether the forces are balanced or not, there will be no radial acceleration when the object is stationary in the inertial frame.

The wording was chosen to maintain accuracy and avoid controversy. And now you are just digging in.David Tombe (talk) 06:27, 1 May 2008 (UTC)

Let's examine the existing introduction. This paragraph here,

In some cases, it is convenient to use a rotating reference frame, rather than an inertial reference frame. When this is desirable, coordinate transformations from the inertial reference frame can be applied.

However, to do this correctly, in the rotating reference frame, a centrifugal force must be applied in conjunction with a Coriolis force for the correct equation of motion to be calculated. The centrifugal force depends only on the position and mass of the object it applies to (and does not depend on its velocity), whereas the Coriolis force depends on the velocity and mass of the object but is independent of its position.

is just clutter.

And it says nothing about any of the real effects that would occur in a centrifuge. Neither does it clarify about not to get confused with centripetal force.

Yet you have nevetheless chosen to revert. Your decision was not based on physics arguments. David Tombe (talk) 06:32, 1 May 2008 (UTC)

"To the extent to which the object or fluid element co-rotates with the frame, a radial acceleration or a hydrostatic pressure is induced." By definition, the actual pressure must be independent of the reference frame. We don't live in an Alice in Wonderland world where from one reference frame something implodes from pressure, but in another the same thing is intact.- (User) WolfKeeper (Talk) 06:47, 1 May 2008 (UTC)

Wolfkeeper, when we rotate a bucket of water, centrifugal force creates a hydrostatic pressure in the water. That is a reality and it only happens in the co-rotation scenario.

At the moment, you are in a state of denial for which there seems to be no cure.

No cure you say! Damn these eyes!- (User) WolfKeeper (Talk) 07:41, 1 May 2008 (UTC)

You are living in a fictitious world in which you want to pretend that a rotating bucket of water is exactly the same thing as a stationary bucket of water as when viewed from a rotating frame of reference.

They are not the same thing. It is a centrifugal force version of the Faraday paradox.

Oh... but the Faraday paradox is completely different.- (User) WolfKeeper (Talk) 07:41, 1 May 2008 (UTC)

I tried to compromise with you and retain the initial line that centrifugal force applies to all the objects.

But you seem to be offended at any suggestion at all that centrifugal force can have any element of reality about it.

You are in denial and you are trying to impose your 'fictitiousist' view of the world on everybody else.

I deliberately worded the article to compromise between the mathematical definition and the layman's understanding. You have reverted it to a version which is clearly ill though out, ommitts important facts, and contains alot of unnecessary clutter.

With my introduction, we won't even need a separate article for reactive centrifugal force. The division is a total mess. David Tombe (talk) 07:17, 1 May 2008 (UTC)

I really have no idea what you're trying to do here. The wikipedia is not the place for your OR on rotational physics.- (User) WolfKeeper (Talk) 07:41, 1 May 2008 (UTC)

Sorry, but based on your performance and stated opinions so far, my policy from here on in is that any non trivial edits in any of these rotation articles by you are going to be reverted at the earliest opportunity unless you include references from reliable sources, and the reliable sources self-evidently agree with your text. It's really nothing personal though.- (User) WolfKeeper (Talk) 07:41, 1 May 2008 (UTC)

Wolfkeeper, You are in a state of denial. Hydrostatic pressure exists in a rotating bucket of water. That is not original research and it does not require a citation. If you check the wikipedia rules, you will see that no citations are needed for facts that are obvious.

You adhere to some strange view of the world in which everything is relative and that absolute facts such as hydrostatic pressure in a rotating bucket of water do not exist. You do not live in the real world.

I doubt if you ever thought of the Bucket argument before. And now that you have been made aware of it, you have calmly stated that you are going to ignore it.

You are not in a position to be editing articles on real physics. You have made an absolute shambles of these pages and for some reason, everybody seems to be too scared to stand up to you.David Tombe (talk) 09:09, 1 May 2008 (UTC)

NPOV and reliable sources

I've just sent a note to David regarding Wikipedia's Neutral Point of View policy and attribution, verifiability and reliable sources principles. I look forward to him providing suitable cites to support his contributions from now on. -- The Anome (talk) 11:15, 1 May 2008 (UTC)

Anome, I'm still awaiting anybody to point out what aspect of that introduction that I wrote was not neutral. I expect that I'll be waiting a long time. When you point out the non-neutral sentences, then I'll supply citations. David Tombe (talk) 12:40, 1 May 2008 (UTC)

David, the addition you made to the introduction concerning centrifuges is, by and large, correct. However, when you made the edit, you removed statements about the rotating frame of reference that were also correct. You haven't improved the article; indeed, it is now less complete than before. ('Fictitious' force in the sense used in classical mechanics does not mean 'imaginary' or 'nonexistent,' as you seem to believe. It's an unfortunate choice of word; but then, it's what is used. 'Inertial,' 'pseudo,' or 'd'Alembert' would be better in my opinion. Please read further down in the article where the semantics is explained. Plvekamp (talk) 16:52, 1 May 2008 (UTC)

Reading this only reinforces the perception that Wikipedia is not a valid source for physics information. The perception of Wikipedia is that it is a source of misinformation, and not a source of correct information. The evident fact is that the editors are unwilling to work out a correct version which incorporates the valid criticism of their attempted edits. Mr Wolfkeeper evidently knows nothing, and denies an experimental fact known for thousands of years to be true. Management has now confirmed that course of action, and validated the view that Wikipedia is more about enforcing certain opinions than benefiting from the criticism of independent scholars and experts. Most physics experts I know consider this web site a joke. Wikipedia is a known bad source of information, due to its policy of copying from others without regard to the quality of the information being blindly repeated. I personally have found so many mistakes here that I dont even attempt to correct them. It is not worth the trouble, considering the editor's attitudes. Sorry, but I do not beleive anything you state regarding physics, since your editiors have shown they dont understand what they are doing. Wikipedia dosen't work, and its failure to take into consideration valid criticism only reinforces the bad information already found here.72.84.69.81 (talk) 17:20, 1 May 2008 (UTC)

Judging by this diff, David's most recent centrifuge-related edit has not only been kept, but integrated into the article. -- The Anome (talk) 17:46, 1 May 2008 (UTC)

Wouldn't it be more accurate to say that centrifuges separate based on density? Mangoe (talk) 20:00, 1 May 2008 (UTC)

Good point. How about "denser element" instead of "heavier particle?" Thus you include both fluid elements and particles in suspension. If anyone disagrees, go ahead and revert my edit and we can discuss. Plvekamp (talk) 20:26, 1 May 2008 (UTC)

Mistakes in the wikipedia are inevitable and are always going to be there. However, if you can show that there is a mistake, with references to it, I will gladly help you to fix any problems that there may be. In terms of comprehensibility and scope this article is not perfect, and probably due to article size and other constraints few articles can ever be perfect, but we need it to be as minimally imperfect as possible.- (User) WolfKeeper (Talk) 21:28, 1 May 2008 (UTC)

Would it be appropriate to include the Euler force in the introduction, since the Coriolis is also included ? Or would angular acceleration of the reference frame be overly complicating the issue ? Plvekamp (talk) 21:53, 1 May 2008 (UTC)

Personally, I think it would overcomplicate the introduction, the most common case is for uniformly rotating frames. It's also not mentioned elsewhere in the article, but I noticed it was missing from the 'see also' section and inserted it.- (User) WolfKeeper (Talk) 22:59, 1 May 2008 (UTC)

Good compromise. Thanks Plvekamp (talk) 23:18, 1 May 2008 (UTC)

The playing down of real effects

This edit war will only be resolved when there is an open realization of what the war is about. What is the undercurrent that is driving it? And after making yesterday's edits and watching the response, I can now tell you all exactly what it is about.

I inserted a clause in the introduction which drew attention to the fact that in co-rotation situations, we obtain an actual outward acceleration or an actual hydrostatic pressure. Somebody correctly altered that to 'pressure gradient'. That is what constructive collaborative editing is all about. Somebody else changed 'heavier' to 'more dense'. Very good. That's the right idea. Keep improving the matter and making it progressively more and more accurate.

Now unusually, for the first time, my edits were not completely erased. These key bits of information, rather than being completely erased, were moved to a section further down the page where scan readers are less likley to go.

Compare this to the excessive invasion of the first line with copious references to the term 'fictitious'.

Clearly we have a party here who are very keen to emphasize the word 'fictititious', and to hide any examples that might undermine the suitability of the term 'fictitious'.

As regards the original research which I keep getting accused of, I'm still waiting to have that pointed out.

Now at the moment, the introduction is still most unsatisfactory. But I'm going to leave the first line alone and try and tidy up the incoherent clutter below it.

A member of the public reading about centrifugal force wants to see examples. They don't want to read about transformation equations that might be used by scientists behind the scenes.

And we have no examples in the introduction. All we have is a very amateurish statement to the extent that the matter is confusing. That's the kind of thing that somebody who doesn't understand the issue would write.

I'm going to make a different edit later today. When it gets erased, as it almost certainly will be, then we can discuss why. And I guarantee that it will all come down to the fact that the ruling party do not like attention being brought to the fact that centrifugal force can have real effects. It is being sold in the first line as a 'fictitious' effect and that's the party line which it seems must be upheld at any cost. David Tombe (talk) 08:29, 2 May 2008 (UTC)

David, thank you for making small, specific edits, and discussing them individually. No-one is denying the reality of these phenomena, or that, within the rotating reference frame, they can be explained in terms of a centrifugal force. As far as I can see, your objection seems to be that for you, labeling centrifugal force "fictitious" is equivalent to calling the phenomena which appear to be caused by centrifugal force fictitious. Perhaps "fictitious force" is an unfortunate name, but it is the most common term used to describe entities such as centrifugal force and the Coriolis force. If you object to the term "fictitious force", would you be happier with any of the other terms for such a force, such as "inertial force", "d'Alembert force", or "pseudoforce"? I also agree with you that coordinate transformation is the key to this, and a mathematical treatment is the only way to properly resolve the apparent paradox. -- The Anome (talk) 09:26, 2 May 2008 (UTC)

Anome, the terminology has never been the main issue, although it's true that I do not like the term 'fictitious force', and I would indeed prefer the term 'inertial force'.

The main issue has been that any attempt to illustrate any semblance of reality surrounding centrifugal force is swiftly removed from the introduction.

Interestingly, one critic yesterday stated that he agreed with my insertions but then ciricized me for having removed other stuff.

So today, I will reinsert a single sentence and not delete the other stuff. I guarantee it will be swiftly deleted.

Then we can discuss why. David Tombe (talk) 10:07, 2 May 2008 (UTC)

Anome, we can now see what has happened. PeR has come along within minutes and deleted it. It is also of interest to note that PeR earlier inserted another reference to back up the idea that the term fictitious force is in widespread use. But nobody is denying that.

This illustrates clearly that PeR is pushing a point of view. He is determined to go over the top to emphasize the 'fictitious' aspect of centrifugal force but to hide all references to everyday phenomena that indicate that there may be an element of reality to centrifugal force.

Now you can see clearly what is going on. We have identified the offending clause. David Tombe (talk) 10:33, 2 May 2008 (UTC)

I think the question here is one of explanatory power. You can explain the same phenomena in two different ways; either in a rotating frame, using Newton's laws with the addition of pseudoforces, or at the cost of some extra difficulty in getting your thinking straight about the various forces involved, in an inertial frame, using Newton's laws alone. While the first explanation is in better agreement with our naive physical intutitions about how the world works, and the calculations are easier to do (to first order), mathematicians and physicists prefer the latter, because it is a simpler explanation that requires fewer conceptual entities and an overall simpler mathematical framework, even if it involves slightly more difficulty in making the necessary calculations. The centrifugal force is "fictitious" in the sense that everything in the system can be explained without it, by choosing an inertial frame of reference; but as far as I can see no-one is denying that the effects that can be ascribed to it in the rotating frame are real, regardless of which system of ideas you use to explain them. -- The Anome (talk) 10:53, 2 May 2008 (UTC)

Anome, the lines which PeR removed related to an effect which is absolute and which doesn't depend on which frame of reference we view it from. That outward acceleration or the associated hydrostatic pressure can be viewed from all reference frames. It is not a fictitious effect. That's why PeR removed it. He doesn't want attention brought to absolute effects in conjunction with centrifugal force.David Tombe (talk) 11:07, 2 May 2008 (UTC)

David, please keep an open mind to the notion that when many editors disagree with your edits, those editors could be right. No one is out to persecute you. This page is the proper place to discuss the article, but your "I'm right and they're trying to silence me" attitude is making it difficult. Plvekamp (talk) 11:13, 2 May 2008 (UTC)

Plvekamp, it was actually you who reverted me this time. Did you have a reason to do so? PeR has now informed me that his reason was that I hadn't provided sources. But we don't need sources for facts that are not in dispute.

Are you disputing the facts that you erased?David Tombe (talk) 13:22, 2 May 2008 (UTC)

Action-Reaction Pair

We are now getting closer to the truth. Of course centrifugal force and centripetal force act as an action-reaction pair in every circular motion situation.

A web link to Donald E. Simanek saying the opposite is not acceptable.

Anybody who claims that centripetal force and centrifugal force do not form an action-reaction pair in circular motion needs to provide a citation from a peer reviewed journal or a reliable textbook. David Tombe (talk) 14:00, 2 May 2008 (UTC)

David, it doesn't work that way: editors are responsible for providing cites for the statements they add to the article, not for providing cites refuting other statements added by other people, on the basis that those statements are self-evidently THE TRUTH unless refuted. You are entirely entitled, per the verifiability policy, to ask other editors for cites supporting their own additions to the article, but if you expect them to do so you should also act in the same way, by providing cites for your own additions, rather than asking them to refute yours. -- The Anome (talk) 15:22, 2 May 2008 (UTC)

From "Facts on File Dictionary of Physics", pg 34 (1999) entry on centrifugal force:

"If a car is moving around a bend, for instance it is forced in a curved path by friction between the wheels and the road...It is sometimes said that the centrifugal force is 'reaction' to the centripetal force - this is not true. (The 'reaction' to the centripetal force is an outward push on the road surface.)"

Moreover, the centripetal force and the centrifugal (pseudo)force cannot be a action-reaction pair since they are acting on the same object. Action-reaction pairs have to act on different forces - the centripetal force from the wall of the centrifuge on the fluid is equal and opposite to (acts as an action-reaction pair with) the force from the fluid on the wall of the centrifuge. --FyzixFighter (talk) 15:47, 2 May 2008 (UTC)

FyzixFighter, The statement that you erased read,

When the wall of the centrifuge applies an inward acting centripetal force such as to prevent further radial acceleration, we will have an action-reaction pair.

The wall acts inwards on the object and the object acts outwards on the wall. That is an action-reaction pair. If you insist otherwsie then you are lying and trying to pull the wool over the eyes of the readers.

Reading your passage above, it is clear that your example doesn't apply to the situation in question, and that you have ended up contradicting yourself. Basically, you haven't got a clue what you are talking about. Your reversion was vandalism. David Tombe (talk) 16:01, 2 May 2008 (UTC)

For the force by the object on the wall, see Reactive centrifugal force. However, the sentence that was removed seemed to say that the centrifugal force was acting on the object, and that it existed before there was any contact between the object and the wall. However, regardless of whether it was The Truth, FyzixFighter was in his rights to remove the statement, since it was disputed (by me, and presumably by the other editors who deleted it also) and unsupported by citations. --PeR (talk) 16:20, 2 May 2008 (UTC)

David, you forgot the sentence before that one,

In cases of co-rotation, the centrifugal force induces an actual radial acceleration on the object. This effect is observed in the centrifuge device.

So, in your edit, the centrifugal (pseudo)force acts outward on the object, and the wall also acts inward on the object. So both these are acting on the same object, they therefore cannot be an action-reaction pair. Moreover, from the article on Newton's laws of motion (in the "Newton's third law: law of reciprocal actions" section):

It is important to note that the action/reaction pair act on different objects and do not cancel each other out.

You wanted a cite that said they don't form a action-reaction pair, and I gave you one. So now it's your turn to provide a source supporting your views.

(and after the edit conflict) How does the citation not apply to the situation in question, and how did I contradict myself? --FyzixFighter (talk) 16:23, 2 May 2008 (UTC)

I can see this is going nowhere. Would you like to rewrite the textbooks as well as wikipedia, David ?? What the other editors are putting in the introduction agrees with the texts. Your edits don't. Please stop sabotaging everyone's efforts. The only statement you have contributed that has been agreed upon is the one example you included on the centrifuge, which was put in the applications section where it belongs. Plvekamp (talk) 16:28, 2 May 2008 (UTC)

FyzixFighter and PeR, The sentence read,

When the wall of the centrifuge applies an inward acting centripetal force such as to prevent further radial acceleration, we will have an action-reaction pair.

The wall pushes inwards on the object and the object pushes outwards on the wall. That is an action-reaction pair. And your citation had nothing to do with this scenario. David Tombe (talk) 16:30, 2 May 2008 (UTC)

Actually, the citation is exactly about this situation. Replace wall with road, and object with car and they are identical. The object pushing outwards on the wall is the reactive centrifugal force (which is addressed by the ending parenthetical in the citation). I had interpreted your original edit to imply that the inward force from the wall on the object forms an action-reaction pair with the centrifugal (pseudo)force acting on the object - this is not true. However, I do agree with your restatement above - "The wall pushes inwards on the object and the object pushes outwards on the wall. That is an action-reaction pair." This is accurate, but was not what your original edit implied. --FyzixFighter (talk) 16:41, 2 May 2008 (UTC)

FyzixFighter, would you then be willing to reinstate the clause, reworded to your own satisfaction?David Tombe (talk) 17:06, 2 May 2008 (UTC)

If it were reworded to be in agreement with reliable sources, then yes I could support it. However, the clause (as I currently understand it) deals with a centripetal force and a reactive centrifugal force, and not the centrifugal force that this article discusses (ie, a force in the rotating frame acting on the object), and so I'm not sure it belongs in the intro. I could see it being added to the third paragraph to address the confusion between the centrifugal pseudoforce on the object and the reactive centrifugal force the object exerts. Propose a rewording of the clause, and we can start working on wording and placement. --FyzixFighter (talk) 17:25, 2 May 2008 (UTC)

FyzixFighter, the very fact that this article has segregated the knock on effect to a different page means that the whole situation is quite hopeless now. So let's forget about action-reaction pairs for now. Wolfkeeper has split the topic and so we are not even permitted to adopt an overview of the events which are taking place. I would actually combine the articles if I knew how to, unless maybe it is an administrator power only. the reactive centrifugal force article is rubbish. It's in an even worse mess than this one and I think everybody is just ignoring it now.

So let's go to the first part of the sentence which you erased. That part drew attention to the fact that things actually accelerate outwards radially when they are undergoing co-rotation. Why did you ersae that clause?David Tombe (talk) 17:51, 2 May 2008 (UTC)

Ok, my problem with that clause is that in the stationary frame, there is no outward, radial acceleration. Looking at the example of a person in the car turning a corner. From the stationary frame, the person is moving in a straight line, as the car turns and moves underneath them. From the rotating frame, this looks like the person is accelerating outward, but this is an artifact of the coordinate transformation into the rotating frame, or, as one source has put it, it is a purely kinematic consequence from transforming into the rotating frame. --FyzixFighter (talk) 18:11, 2 May 2008 (UTC)

FyzixFighter, I thought that the whole introduction was about things as viewed from the rotating frame. And all I did was give an example of a situation where the radial acceleration was real. And you erased it.

Would you consider reinstating that sentence?David Tombe (talk) 18:35, 2 May 2008 (UTC)

Plvekamp, I inserted a clause in the introduction which is true and which draws attention to the real aspects of centrifugal force. You are clearly one of the 'Fictitious Party' that feels uncomfortable about this.

Rather than continuing to merely state that I am wrong and delete my entries, can you please explain exactly what it is about the centrifuge effect that makes you feel so uncomfortable?David Tombe (talk) 16:37, 2 May 2008 (UTC)

It doesn't work like that. The statements in the intro are cited in textbooks. You want something different there, the onus is on you to prove it with citations, which you have so far refused to do. I am completely comfortable with the centrifugal effect being due to inertia in the inertial frame, and centrifugal pseudoforce in the rotating frame. Plvekamp (talk) 16:44, 2 May 2008 (UTC)

Plvecamp, Does a co-rotating object accelerate outwards or not?David Tombe (talk) 17:11, 2 May 2008 (UTC)

From which frame of reference? This is an important distinction. And is that object under a constraint, such as the side of the car or the end of the test tube?

If it is free (object in car, particle at top of test tube not encountering resistance):

- From inertial frame: No acceleration, no force, moves in straight line (and approaches end while doing so)
- From rotating frame: Acceleration outward in accordance with centrifugal pseudoforce covered in this article

When it encounters restraint (door of car, particle encountering resistance or at end of test tube)

- From inertial frame: Centripetal force exerted by restraint on object, object accelerates radially inward
- From rotating frame: No acceleration, object is stationary if frame rotates at same speed as constraint

Plvekamp (talk) 17:28, 2 May 2008 (UTC)

Plvekamp, when I say a radially outward acceleration, I don't need to specify a frame of reference. If somebody is sitting in a car that is driving in a circle, will they experience a radially outward acceleration that will cause them to slide to the side door? The answer is either yes or no. We don't need to mention the word 'fictitious' or 'pseudo'.David Tombe (talk) 17:42, 2 May 2008 (UTC)

David, when your talking about what "a person sit in a car driving in a circle" experiences, you are implicitly specifying a frame of reference. Namely, what a person experiences can only be described in a co-moving frame. Such a frame is typically non-inertial and will thus contain psuedoforces (or however one wishes to call them) from the perspective of this observer/person these forces are very much real. As you state the person feels himself pushed towards the outward door. An other observer will understand this diffently. An observer from an inertial frame will see the person in the car being forced to move in a circle by force exerted on him by the car.(TimothyRias (talk) 14:32, 5 May 2008 (UTC))

This is so outrageous - "I don't need to specify a frame of reference" - that I'm at a loss for words. That has to be the most naive statement you've uttered yet. If you actually believe that, then nearly all of mathematical physics is beyond your understanding. Plvekamp (talk) 18:02, 2 May 2008 (UTC)

Plvecamp, your reply above has given you away. You are not genuine. You won't answer the question because the answer would expose a real outward radial acceleration. You live in a fictitious world of denial and you are a wikipedia vandal that the administration can't see through. David Tombe (talk) 19:27, 2 May 2008 (UTC)

David, you seem to be telling people that "they are living in denial" quite frequently. [1] [2] [3] [4] Such statements are unproductive, and will only lead to an escalating degree of impoliteness in the discussion. I'd appreciate it if you in the future try to only comment on the content, and not on the contributor. Thank you. --PeR (talk) 20:21, 2 May 2008 (UTC)

Donald E. Simanek

A link to Simanek's site is quite acceptable. He is a physics professor, after all. Mangoe (talk) 16:55, 2 May 2008 (UTC)

Thanks Mangoe. I'll bear that in mind for future citations. The author only needs to be a physics professor.

My own view is that Donald E. Simanek is badly wrong, and it seems that he is the source of misinformation that has been guiding this 'Fictitious Party' that are dominating these pages. David Tombe (talk) 17:10, 2 May 2008 (UTC)

If you aren't a physicist, then frankly I'm not really all that interested in your challenge to Simanek et al. Never mind my own understanding of the matter; he has credentials, and as far as I can tell, you don't. Mangoe (talk) 17:50, 2 May 2008 (UTC)

Who is this guy??? Please explain which link is the link you are talking about. When you write something you need to be clear about what you mean. —Preceding unsigned comment added by 72.84.70.6 (talk) 20:55, 3 May 2008 (UTC)

Orbital Theory

Steve, we'll continue this in a new section. You left off at,

David, I'll respond assuming you meant in the inertial frame, since that appears from context to be what you're saying. The acceleration of a rotating object is radially inward in any system of coordinates for the inertial frame. Here's polar, for example: The expression for outward radial acceleration is (r double dot - r (theta dot)^2). r isn't changing, so r-double-dot is zero. Theta is changing, with theta-dot = v/r. So you get (0-r(v/r)^2)=-v^2/r acceleration in the outward radial direction, which corresponds to +v^2/r acceleration in the inward radial direction. Exactly the same result as you can derive with cartesian coordinates, or with any stationary coordinate system, or with no coordinate system at all! (See the article uniform circular motion for a coordinate-independent derivation.) If you don't understand this, I promise that you'll find a clear explanation in an intro college-level physics textbook. Please do this simple step now, not later. --Steve (talk) 16:32, 2 May 2008 (UTC)

Steve, I'm quite familiar with orbital theory concerning hyperbolas, parabolas, and ellipses. I've had to solve many a difficult problem in this field.

Let me begin with a very simple example. Consider an object high above the Earth that has got zero tangential speed. The only force acting will be gravity, radially downwards. The object will accelerate downwards and the acceleration due to gravity will be equal to r double dot.

Now consider a circular orbit. There will be an additional outward centrifugal force given by mv^2/r. In this case, r double dot will be equal to zero. There will be no net radial force or acceleration.

True. For once. There's no NET acceleration- the gravitational acceleration balances the centrifugal acceleration, and in the rotating frame of reference there is no coriolis force if there is no motion in that frame.- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

Good. But you are now in disagreement with Steve and FyzixFighter below.David Tombe (talk) 07:00, 3 May 2008 (UTC)

In elliptical orbits there is a constant oscillation between whether the centrifugal force is greater or the gravity force is greater.

Yes, due to variations in coriolis and in centrifugal and gravity in the rotating frame you get an elliptical orbital motion with a focus at the stationary point with the same orbital period.- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

No Wolfkeeper. There is no Coriolis force involved in central orbital theory. Kepler's law of areal velocity gets rid of the tangential components where you find the Coriolis force term. David Tombe (talk) 07:00, 3 May 2008 (UTC)

I'm afraid that isn't the case; the angular momentum is constant (i.e. areal velocity is constant), but not the angular velocity. The reference frame rotates at constant angular velocity while the body doesn't (higher angular velocity close in, lower further out).- (User) WolfKeeper (Talk) 07:32, 3 May 2008 (UTC)

If we consider an ellipse in polar coordinates, centered on the focus, and solve it, we end up with exactly two radial accelerations. There will be an inverse square law acceleration inwards, and a v^2/r acceleration outwards. Centrifugal force is a very real thing.

Now lets get to the point. Your problem with all this is that it contradicts the pet theory that is being pushed on these pages by the 'Fictitious Party'.

That theory is that when an object is at rest in the inertial frame, it will be seen to trace out a circular motion when viewed from a rotating frame. Your argument is that there is a net inward fictitious centripetal force which is the sum of an outward centrifugal force and an inward Coriolis force which is twice as strong.

You will agree that this is the pet theory that the 'Fictitious Party' are trying to promote on these pages. Indeed there was once an entire section devoted to this idea on these pages. It was considered to be much more important than examples of the real effects which your colleagues are currently at this very moment in time trying to hide.

Your theory is wrong to the backbone on a number of counts.

(1) The transformation equations for rotating frames, only apply to co-rotation. This is clear when we look at the derivation. The angular velocity term ω which is ostensibly the angular velocity of the rotating frame, is in fact tied in with the tangential velocity of the particle in question. This is clear by virtue of the fact that it is one of two components of the particle velocity.

I'm sorry, but this is simply wrong, and shows that you have not followed the derivation at fictitious force- it nowhere assumes corotation. Such a theory would be pretty useless in the real world in any case. If you start from falsehood, you can only end up at another falsehood.- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

Wolfkeeper, the derivation at fictitious force only begins after that stage. It begins by already assuming that we know where the ω X term came from. You need to go back further to see that the ω term relates to the tangential velocity of the particle in question.David Tombe (talk) 07:06, 3 May 2008 (UTC)

No, it comes from the velocity increment you get on any particle whatsoever when you go from one reference frame to another which is rotating at speed w relative to the first frame. And this is completely general, it applies to all velocities of particles in the initial and final frames whether they corotate or not.- (User) WolfKeeper (Talk) 07:44, 3 May 2008 (UTC)

(2)In the limit, the v term then becomes the radial velocity. Hence there is no Coriolis force in the radial direction. The Coriolis force and the centrifugal force can never act in the same direction because they are two mutually perpendicular aspects of the same thing. Hence the idea that the Coriolis force could be producing an inward radial force is absolute nonsense.

Um. Why is there a coriolis force anyway? It comes out of the derivation for centrifugal force/acceleration. But if something is corotating then it doesn't move in the rotating frame of reference, so no coriolis force. Strangely, all these physicists keep talking about coriolis, and how it influences the weather on Earth's rotating surface, but you say it doesn't exist at all. Why do you think that is? Could all these weather men have got it wrong all this time and been waiting for the genius of David Tombe to point it out? That NOBODY had ever worked it out as well as you? That's a lot of very smart guys, and they each would have been famous if they had found a hole in the theory, they would have been well-motivated. Or could it be that your corotation idea is a complete red herring for your thinking?- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

Wolfkeeper, something can be co-rotating and moving radially in a rotating frame of reference. When that occurs, we get Coriolis force, unless of course the radial motion is the deflection associated with the centrifugal force.

Irrelevant, coriolis applies to non corotating orbjects. None of the objects in the atmosphere corotate. Your understanding of these pseudoforces only apply to uninteresting cases where these equations would be unnecessary.- (User) WolfKeeper (Talk) 08:01, 3 May 2008 (UTC)

You are totally misrepresenting me on that next point. If you go to the Coriolis force page, you will see that I am actually the one arguing that the Coriolis force exists in the weather, and that it is real.David Tombe (talk) 07:00, 3 May 2008 (UTC)

Yes, but the coriolis force acts at 90 degrees to the *velocity*, not the radial velocity. That's why you get these nice largely circular patterns. Nothing in a swirling cyclone or anticyclone corotates with the Earth.- (User) WolfKeeper (Talk) 08:01, 3 May 2008 (UTC)

(3)Even if we ignore points (1) and (2), the final result comes out to be a net inward radial acceleration. That is not circular motion. Circular motion requires a net zero radial acceleration.

Careful here. Stationary motion or motion in a straight line requires a net zero radial acceleration. Movement in a circle requires a (psuedo)force to rotate the velocity vector. You know- Newton's second law? You may have heard of it.- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

Wolfkeeper, circular motion means a net zero radial acceleration. You already agreed with me above that in a circular gravity orbit, the centrifugal force cancels out with gravity.David Tombe (talk) 07:00, 3 May 2008 (UTC)

Incidentally, it's trivial to show this. If you differentiate the motion of a particle at x=cos(theta*t), y=sin(theta*t) twice with respect to time, you get the net acceleration. You will find it to be precisely radial, and inward. It is NOT zero. That is true in rotating reference frames as well as inertial ones.- (User) WolfKeeper (Talk) 19:58, 2 May 2008 (UTC)

Wolfkeeper, nobody was disputing that in cartesian coordinates we only see the centripetal acceleration. But in your theory about the artificial circle, you are using polar coordinates. So why bother mentioning Cartesian coordinates? And why do so in connection with simple harmonic motion?David Tombe (talk) 07:00, 3 May 2008 (UTC)

So the pet theory of the 'Fictitious Party' is wrong.

When an object is stationary, nothing happens. There is no centrifugal force. There is no hydrostatic pressure gradient induced in a bucket of water.

Those things only happen when the object co-rotates.

And at the moment, your colleagues are desperately trying to hide any references to situations involving co-rotation that result in real physical effects.

There is a group of them who are winning on numbers but who clearly haven't got the first clue about physics but seem to presume that they have.

I would have thought that you would have been intelligent enough to see right through all this, unless perhaps you have got some vested interest in playing along.

But it is all one big fraud. David Tombe (talk) 17:37, 2 May 2008 (UTC)

David, all the three cases of the falling object, circular orbit and elliptical orbit can also be solved in terms of coordinates and forces measured in an inertial frame, and will give exactly the same results as those above without any need to consider pseudoforces. In general, converting to an inertial frame from a rotating frame generates the same physical solutions, but without the need for pseudoforces.

Given these two possible interpretations, physicists choose the inertial frame interpretation, with its simpler physical laws, following the principle of Occam's Razor. Centrifugal force and Coriolis force are not wrong, so much as unnecessary. There is nothing to stop you from sticking with the rotating frame/pseudoforce interpretation, and your equations will continue to produce with exactly the same physical solutions, hydrostatic pressure and all, as the inertial frame/no pseudoforce interpretation, but you will be making life unnecessarily difficult for yourself in solving all but the simplest problems.

Have you considered the possibility that your disagreement with everyone else editing this page, and their agreement with one another in their differing interpretation (which includes your interpretation as a special case using d'Alembert forces), might be because they are -- independently from one another -- correct in their conventional interpretation of the underlying physics, as opposed to there being an organized conspiracy by desperate, unintelligent people to suppress THE TRUTH, which is apparent only to you? -- The Anome (talk) 18:30, 2 May 2008 (UTC) [Updated 18:52, 2 May 2008 (UTC)]

Anome, I knew that already. I know that coordinate transformations don't effect physical reality. So what's your point in relation to the point that I was making to Steve?David Tombe (talk) 19:15, 2 May 2008 (UTC)

Please see above where David told me "I don't need to specify a frame of reference" when I asked him which frame he was referring to. Make your own conclusions. Plvekamp (talk) 18:43, 2 May 2008 (UTC)

Plvecamp, if we are already talking about a radially outward motion, then we don't need to specify a coordinate frame. You haven't answered my question. Will the person in the circularly moving car experience a radilly outward acceleration towards the side door or not? It's a 'yes' or 'no'. There is no need to cloud the answer with reference frames, or words like 'fictitious' or 'pseudo'.David Tombe (talk) 19:12, 2 May 2008 (UTC)

David, for some wierd reason you can't remember how my username is spelled. The answer depends completely on the frame of reference. From an inertial frame, the card door is accelerating toward the person. From a rotating frame, the person is accelerating toward the car door. Same physical result, different accelerations due to differing frames of reference. What's so difficult to understand ??? Sorry I'm sounding grumpy, but this argument is starting to get to me. Time for a break; if you have any more questions ask somebody else. I'm going to leave this topic for awhile and cool off. "I don't need to specify a frame...." AARRRGGGHHHH!!!!!!!!!! Plvekamp (talk) 19:36, 2 May 2008 (UTC)

Alright, I think I might see where you're coming from, and why we may be disagreeing. A person in the car will naturally take the car as his reference frame. When the car turns, he will experience the centrifugal force outwards - as described in the car's reference frame. BUT he is observing this from inside the car, which is turning ! This is a rotating reference frame ! YES, he experiencing a radially outward acceleration ! This is due to his inertia - His body is trying to go in a straight line per Newton's First Law. But from the viewpoint of someone observing from outside the car (this is an inertial reference frame), the car is turning and the person will continue in a straight line until he encounters a centripetal force (car door). Note that in this ideal example we are ignoring car seat friction. And with that I'm really REALLY going to depart this topic for awhile. Plvekamp (talk) 20:15, 2 May 2008 (UTC)

David, just because r double dot is zero does not mean that there is no radial acceleration, but let's walk through this slowly, so we can identify were you disagree. For a perfectly circular orbit in a stationary frame, using polar coordinates:

1. $r(t)=r,\theta (t)={\frac {vt}{r}}$ where r, the radius, and v, the tangential speed, are both constants
2. ${\vec {r}}=r{\hat {r}}$ is the position vector
3. ${\dot {\vec {r}}}={\dot {r}}{\hat {r}}+r{\dot {\hat {r}}}=0+r{\dot {\theta }}{\hat {\theta }}=v{\hat {\theta }}$ gives us the velocity vector
4. ${\ddot {\vec {r}}}={\dot {v}}{\hat {\theta }}+v{\dot {\hat {\theta }}}=0+(-v{\dot {\theta }}{\hat {r}})=-{\frac {v^{2}}{r}}{\hat {r}}$ gives us the acceleration vector

So even though r is a constant, the acceleration does have a radial component. Now where do you disagree. --FyzixFighter (talk) 18:44, 2 May 2008 (UTC)

FyzixFighter, in your number (3), why did you drop the radial velocity component r dot r hat?

OK. I see. You assumed that because we have a circular motion that we can drop r dot. But we can't drop anything until we have derived the full acceleration formula.

What you did was derive the acceleration purely from the velocity vector. This is quite legitimate but it doesn't specify a cordinate frame and so the result is a vω at right angles to the direction of motion. This is the parent quantity to both the Coriolis force and the centrifugal force.

Had you gone to the full acceleration expression, this term would have been expanded into mutually perpendicular components. The radial component is the centrifugal force and the tangential component is the Coriolis force.

In this situation, r double dot must be zero in a circular orbit because the centrifugal force outwards cancels with the gravitational force inwards.David Tombe (talk) 18:52, 2 May 2008 (UTC)

By the way, I can also recommend prolonged contemplation of this animation. -- The Anome (talk) 18:55, 2 May 2008 (UTC)

David:I dropped the r dot r hat part in (3) because r dot is zero (r being constant). --FyzixFighter (talk) 19:06, 2 May 2008 (UTC)

Yes, I saw that. We must have cross wired. See my full reply above. David Tombe (talk) 19:07, 2 May 2008 (UTC)

This derivation is to show you that even in a stationary frame, using polar coordinates and not cartesian coordinates, then acceleration is radially inward and not zero. I did specify a coordinate frame at the very beginning, a stationary, non-rotating frame with polar coordinates. How can r dot be anything but zero. If the r, the distance, is constant than r dot is 0 and r double dot is 0. Basic calculus. Do you have a problem with (1) given that this is a stationary, non-rotating frame? But just for kicks, the whole thing, putting in zeros only at the end:

1. $r(t)=r,\theta (t)={\frac {vt}{r}}$ where r, the radius, and v, the tangential speed, are both constants
2. ${\vec {r}}=r{\hat {r}}$ is the position vector
3. ${\dot {\vec {r}}}={\dot {r}}{\hat {r}}+r{\dot {\hat {r}}}={\dot {r}}{\hat {r}}+r{\dot {\theta }}{\hat {\theta }}={\dot {r}}{\hat {r}}+v{\hat {\theta }}$ gives us the velocity vector
4. ${\ddot {\vec {r}}}={\ddot {r}}{\hat {r}}+{\dot {r}}{\dot {\hat {r}}}+{\dot {v}}{\hat {\theta }}+v{\dot {\hat {\theta }}}={\ddot {r}}{\hat {r}}+{\dot {r}}{\dot {\theta }}{\hat {\theta }}+{\dot {v}}{\hat {\theta }}+(-v{\dot {\theta }}{\hat {r}})$ gives us the acceleration vector

Now, from (1) r is constant which kills the first (r double dot=0)and second term(r dot=0), and the tangential speed, v, is constant which kills the third term. This again leaves us with just the fourth term, a radially inward acceleration for the stationary frame in polar coordinates. --FyzixFighter (talk) 19:46, 2 May 2008 (UTC)

FyzixFighter, before your equation (4) can have any meaning, we have to account for all the terms. Let's forget about the 'theta hat' terms because we are not interested in angular acceleration.

Now supposing the circular motion was a gravity orbit. Where do you see the inverse square law gravity term fitting into equation (4)? Does it go to the general acceleration term on the left hand side, or does it go to the r double dot term on the right hand side?David Tombe (talk) 20:06, 2 May 2008 (UTC)

Account for the terms, as in give them names? Sorry, I don't see why we need to do this. This is a simple derivation with no hidden assumptions. All the assumptions I'm making are in (1) and in the statement that this is a stationary frame. Your argument, if I understood it correctly, is that in polar coordinates the radial acceleration for circular motion is zero. This derivation shows that you are wrong. The theta hat terms don't matter, not because we're not interested in angular acceleration, but because r dot is zero and v dot is zero. For circular motion in a stationary frame with polar coordinates, the acceleration in the tangential (theta hat) direction is zero and the acceleration in the radial (r hat) direction is non-zero.

The gravity, inverse square law question seems a bit non-sequitur. It's not there in (4) because (4) is just the general acceleration for polar coordinates in a non-rotating frame. If we were to combine (4) with Newton's 2nd law of motion (which requires a stationary frame) and Newton's law of gravity, then we would get the equations of motion, but the only terms appearing in the sum of forces would be gravity - no centrifugal force, no coriolis force. --FyzixFighter (talk) 20:36, 2 May 2008 (UTC)

In other words, David, acceleration is the second derivative of position. If you know the position as a function of time, then you know the acceleration by differentiating twice. If the position as a function of time happens to be "uniform circular motion", then this is a proof that the acceleration is v^2/r inward, as is well-known, and taught in every intro college physics course. Now the question arises, if an actual particle had this motion, what would be the forces on it? Well, force equals mass times acceleration, so you would get this motion if and only if there were a net, total inward force of mv^2/r. This force can come from gravity, for example, or from a string. Note that the force is not and cannot be "balanced out" by any other force -- if it were, then the net force would be zero, so the total acceleration would be zero, so the direction of the velocity wouldn't be changing, and it wouldn't be circular motion! Do you dispute Newton's second law? Or do you dispute the calculation of the acceleration of a uniformly-rotating point? :-P --Steve (talk) 22:32, 2 May 2008 (UTC)

Steve and FyzixFighter, it would be a help if the two of you discussed this together and appointed a spokesman to ask me the questions.

Equation (4) tells us nothing until we know exactly what scenario we are applying it to and what the forces involved are. I asked FyzixFighter were he wanted to put the gravity force if it were a circular gravity orbit, and I didn't get a clear response.

Lets then deal with an easier situation. Let's deal with a weight being swung around on the end of a string. We use the symbol T to represent the inward tension. Can you please present me with equation (4) as per this scenario, showing me where you have inserted the tension T.David Tombe (talk) 06:45, 3 May 2008 (UTC)

Hang On! I think I now see the source of alot of the confusion. You have been assuming that the v^2/r term is centripetal force. In fact, this error is mirrored in your pages on Kepler's laws. I've copied a chunk here,

"So the position vector

$\mathbf {r} =r{\hat {\mathbf {r} }}$

is differentiated twice to give the velocity vector and the acceleration vector

${\dot {\mathbf {r} }}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\hat {\mathbf {r} }}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},$

${\ddot {\mathbf {r} }}=({\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\hat {\mathbf {r} }}})+({\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\dot {\theta }}{\dot {\hat {\boldsymbol {\theta }}}})=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.$

Note that for constant distance, $\ r$, the planet is subject to the centripetal acceleration, $r{\dot {\theta }}^{2}$, and for constant angular speed, ${\dot {\theta }}$, the planet is subject to the coriolis acceleration, $2{\dot {r}}{\dot {\theta }}$.

Inserting the acceleration vector into Newton's laws, and dividing by m, gives the vector equation of motion

$({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}=-GMr^{-2}{\hat {\mathbf {r} }}$ "

This maths is all correct but he has wrongly referred to the centrifugal force term as the centripetal force. How could it be the centripetal force when it was derived from a parent term 'v times ω' of which the other component is the Coriolis force?

This seems to be a common error. The v^2/r term is unequivocally the centrifugal force term and in the full orbital equation (radial component), the centrifugal force outwards cancels with the gravitational force inwards in circular orbits.

The term can't possibly mean centripetal force because it is a general equation for acceleration which doesn't assume any particular kind of motion. It would certainly not incorporate centripetal force as a matter of course. The fact that the mutually perpendicular component of it is Coriolis force means that it undoubtedly refers to centrifugal force.David Tombe (talk) 10:21, 3 May 2008 (UTC)

Nope. He has correctly referred to centripetal force as centripetal force. One way you can tell is that it's pointing inward, whereas centrifugal force can only point outward.

Also, note that the auther correctly says it's "coriolis acceleration", not coriolis force. The acceleration is r-dot*theta-dot, while the force that causes this acceleration is unspecified. --Steve (talk) 01:03, 4 May 2008 (UTC)

Steve, I'm going to ignore the issue of whether we talk about force or acceleration. We are talking about inertial forces here so it is quite irrelevant.

Now can we get to the key point. You are quite wrong in thinking that the v^2/r term is centripetal force. How could it be? How would a general expression for acceleration suddenly produce a centripetal term in conjunction with a Coriolis term? The parent inertial term vXω expands in two mutaully perpendicular components in polar coordinates. One is the Coriolis term and the other is the centrifugal term. In fact it is quite ridiculous to think that it could possibly be referring to the centripetal force.

Let's consider how that equation is used in orbital theory. The term that you think is a centripetal term is brought over to the left hand side to join the gravity expression. Hence gravity will have a negative sign and the term that you think is the centripetal term will have a positive sign. on the right hand side, we have r double dot.

So we have a second order differential equation in r.

If r double dot is zero, then the gravitational force inwards is exactly cancelled by the centrifugal force outwards.

If you are correct, it would imply that centripetal force is something that occurs naturally. That is not so. The gravitational force IS the centripetal force in this situation, and the v^2/r term is the centrifugal force. David Tombe (talk) 03:22, 4 May 2008 (UTC)

Trying to find the disagreement

David, I think I've come to understand a key yet subtle point of disagreement. This is an honest attempt to understand how you understand the physics; I think we might be disagreeing on how we define radial acceleration. So let me set the stage. This is a stationary frame described by polar coordinates. We have an object move in some arbitrary fasion in this frame, and whose position is defined by the coordinates $r(t)$ and $\theta (t)$. In this case, what is the proper expression for the radial acceleration, defining the radial acceleration as $a_{r}={\ddot {\vec {r}}}\cdot {\hat {r}}$:

1. $a_{r}={\ddot {r}}$
2. $a_{r}={\ddot {r}}-r{\dot {\theta }}^{2}$

Or do you disagree that the radial acceleration should even be defined as $a_{r}={\ddot {\vec {r}}}\cdot {\hat {r}}$? --FyzixFighter (talk) 04:41, 4 May 2008 (UTC)

FyzixFighter,

1. $a_{r}={\ddot {r}}-r{\dot {\theta }}^{2}$

is the correct expression for radial acceleration. The signs can however be confusing and so it is important to match it all up correctly with the physics. Remember, the signs in the above expression are only a result of vector calculus notation.

Hence when we set up a differential equation for a gravity orbit, we have,

-GM/r^2 + v^2/r = r double dot

In other words, in a circular orbit, r double dot is zero, therefore the inward gravity cancels with the outward centrifugal force.

More generally in elliptical orbits, the two alternate between which is the greater at any point in time.

In the artificial circle which is the subject of this controversy, r double dot will also have to be zero. but since the net force is not zero, then we have a problem.

I can assure you that when we differentiate the polar equation for a conic section (hyperbola, ellipse, parabola) in order to obtain the acceleration, that the final result will come out to be, not only an inverse square law inwards, but also a v^2/r acceleration outwards. David Tombe (talk) 06:13, 4 May 2008 (UTC)

Ah, and here's where we disagree. You can't just pull whatever terms you like to the other side and suddenly call it a force. If we instead pull over the r double dot term to the left hand side of the equation, can we call that a force, too? At a simplistic level, in physics a force is whatever appears on the left hand side of F_net=m*a. In the case of the gravity you bring up, the instant you pull the m*v^2/r term over to the left hand side, the right hand side is no longer the acceleration. And once the acceleration label no longer applies to the right hand side, the label of force no longer applies to the left hand side; it's just a differential equation then. It seems to me that this is a key point of disagreement; you can't rearrange the differential equation, moving terms from one side to the other and then reapply the original physics labels. Physics doesn't work that way. --FyzixFighter (talk) 06:51, 4 May 2008 (UTC)

FyzixFighter, I'm sorry but you're very badly mistaken here. The equation that I wrote out is the central force orbital equation. That is the equation that is used to solve central force orbital problems. I solved many a complex problem using that equation.

The equation which you have used is a general acceleration equation derived from a position vector using vector calculus theorems and notation. Whereby I have always been impressed by the amount of information that this equation reveals, we can not allow a quibble about terminologies to alter the reality of the final central force orbital equation.

Your equation effectively exposes the fact that centrifugal force is inherent in straight line motion as viewed from polar coordinates. In fact, I ought to draw the attention of Brews to that point.

But there is no further argument regarding the form of the orbital equation. One side contains a second order time derivative of the radial distance and the other side contains an inward gravity force and an outward centrifugal force. You can call that second order time derivative whatever name you like. But in circular orbits, it will be zero.

And if you try messing around with the signs in the orbital equation, you will no longer have the orbital equation. If you want a conic solution, then that is the equation. David Tombe (talk) 08:56, 4 May 2008 (UTC)

Plvekamp's response

Plvekamp has finally responded,

From a rotating frame, the person is accelerating toward the car door.

Now the whole introduction is about centrifugal force which it claims is a force only ever viewed from a rotating frame.

I added a line saying that in situations of co-rotation, an object accelerates radially outwards.

Plvekamp erased this sentence on the specious grounds that this true fact didn't agree with the references.

What references was he talking about? Was he referring to all the references that were wheeled in to enforce the fact that the term 'fictitious' is widely used?

So can we conclude that Plvekamp sacrificed reality in order to comply with the references?

If a centrifuge proves to us that centrifugal force is a real and absolute effect, but the references tell us that this shouldn't be so because the force is question is only a fictitious force, then rather than question the references, we should be better to erase the sentences that draw attention to these inconvenient truths.

Plvekamp, it's about time that you opened your eyes a bit to what's going on in the world around you.David Tombe (talk) 20:17, 2 May 2008 (UTC)

I will no longer respond to your goading, David. I have tried to civilly respond, and you have continually misunderstood my answers. Nowhere have I said that centrifuges don't work or that car passengers don't experience centrifugal force in a turning car. These phenomena are entirely explicable by inertia. I'm leaving it to others to explain the physics to you. Plvekamp (talk) 20:46, 2 May 2008 (UTC)

If you weren't denying those phenomena, then why did you erase mentions of them in the introduction?David Tombe (talk) 06:27, 3 May 2008 (UTC)

I will no longer respond to your goading, David. Plvekamp (talk) 12:12, 3 May 2008 (UTC)

One last request

David, is there any conceivable argument that might convince you that you are wrong, or are you simply committed, as is suggested by your most recent response above, to promulgating the WP:TRUTH as you see it?

The reason everyone else in this discussion appears to disagree with you, whilst all agreeing with one another, is that they are describing the apparent phenomenon of "centrifugal force" in rotating non-inertial frames in terms of inertial effects within standard Newtonian physics. This has been the standard physical interpretation of this phenomenon for several centuries, and is not likely to change. On reviewing this very lengthy discussion, I can see that this has been explained to you over and over in many different ways, carefully and politely, by numerous different people, with only you taking the dissenting position.

You are unlikely to succeed in ever getting your views represented in the article if you continue in this way. Here's why.

Wikipedia is a tertiary source; it summarizes the information in secondary sources, such as peer-reviewed scientific papers, physics textbooks, and other texts written by qualified physicists. It is not a mechanism for determining the WP:TRUTH; we accept that people disagree about just about everything, and we try to reflect this in our articles. For this reason, we have a set of ground rules for editing here which explicitly try to avoid determining truth here on Wikipedia, relying instead, wherever there is controversy, on restricting ourselves to opinions which can be attributed to external, verifiable, reliable sources.

If you want to change the article, and have your changes kept, you must, like every other editor here, abide by Wikipedia's basic ground rules, namely

• Adhering to a Neutral point of view whilst avoiding giving fringe views undue weight.
• Attributability
• Verifiability
• Reliable sources
• No original research

Furthermore, we have another requirement: that editors conduct themselves according to our civility policy. Statements that imply that other editors are acting in bad faith, lack intelligence, or are conspiring against you, go against that policy. Repeated breaches of the civility policy may result in accounts being blocked from editing.

Unfortunately, a personal conviction, no matter how strong or sincere, that your views are the WP:TRUTH does not override these policies and guidelines. -- The Anome (talk) 21:53, 2 May 2008 (UTC)

Anome, the argument is not over yet, so it is far too early to be deciding who is right and who is wrong. There are still a number of key issues to be highlighted.

And as regards this statement by you "they are describing the apparent phenomenon of "centrifugal force" in rotating non-inertial frames", the evidence is quite to the contrary. Yesterday, I was the one who put such entries into the introduction, and they were swiftly erased.

On the issue of politeness, you very much seem to be overlooking the responses which I received from some of your editors when I first began editing this page. David Tombe (talk) 06:34, 3 May 2008 (UTC)

David, please re-read what I wrote above. It's not about who is "right" or who is "wrong": where there is controversy, and agreement cannot be reached through argumentation, Wikipedia's policies require content disputes are ultimately decided by applying the principles I listed above. If you want to provide "evidence to the contrary", you must provide citations to attributable, reliable, verifiable sources that directly support your statements; WP:original research and synthetic arguments are not suitable alternatives to this.

Unless you can work within Wikipedia's rules, the "argument" is irrelevant, and has been for some time; no amount of repetition of your position in ways that do not follow Wikipedia's content polices will make Wikipedia's policies adapt to your desires. If you do not want to abide by Wikipedia's policies, you might want to consider choosing another forum for your contributions. -- The Anome (talk) 12:27, 3 May 2008 (UTC) [Updated 12:46, 3 May 2008 (UTC)]

Anome, you know perfectly well that the edits that I made yesterday were not about ideas that are contrary of current theory. I drew attention to the actual acceleration that occurs outwards when an object co-rotates with a rotating frame. An example would be a passenger in a car getting swung to the side door as a car goes round a corner.

You know fine well that that was not a controversial sentence. You are misrepresenting the situation by continuing to imply that I was trying to insert controversial clauses into the article.

Plvekamp, PeR, and FyzixFighter removed that sentence because they are uncomfortable with the truths inherent in it. Their actions were essentially vandalism which you could have prevented but you chose not to do so. David Tombe (talk) 12:39, 3 May 2008 (UTC)

David, please provide a cite to a reliable, verifiable, attributable source that supports your sentence: if you can do so, we can move forward. Otherwise, you are doomed to repeat this cycle over and over. If what you say is common knowledge, it should be easy to find such a reference. Even if it is merely a significant fringe position, it should still be possible to find a cite. If you can't find a cite, you might want to consider the possibility that your statement represents a fringe position without significant support. -- The Anome (talk) 12:46, 3 May 2008 (UTC)

Anome, I'm not going to bother. That wasn't the issue. I have no intention of going to search for a citation for such a trivial and undisputed fact. It wasn't erased because there was no citation. That was just the cover story. It was erased for other reasons, and the point was proved.

By the way, I am watching your efforts to re-word the introduction. Note what Woodstone says over on the Coriolis force talk page.

There seems to be a school of thought that is saying that the term fictitious actually means that it refers to a mathematical term which comes into effect only in the accelerated frame (in this case, the rotating frame) as an alternative way of describing real effects.

I don't think that that is the universal interpretation of the term fictitious. I think you will find that some of the editors here will try and slowly but surely graft it back to the extent that it literally means that the effects can only be viewed in the rotating frame.

If what you are saying is true, RRacecarr and PeR wouldn't have cocnsistently reverted my removal of the word 'apparent' on the Coriolis page.

I would perhaps tend to agree with your amendments if I am interpreting you correctly. You are saying that these effects are real but best dealt with mathematically by what we term 'fictitious forces'. If that is so, I think that you will also agree with me that the term 'inertial force' is infinitely superior. David Tombe (talk) 15:28, 3 May 2008 (UTC)

For what it's worth, David, I completely agree with your last two sentences. One sentence agrees with the explanations in current textbooks, in relation to rotating reference frames. The other sentence is a purely personal preference in terminology, which we also share. Having said that, I still insist that statements you provide in the article be backed up by citations per Wikipedia policy. I will do the same. Plvekamp (talk) 16:43, 3 May 2008 (UTC)

PlveKamp, I think that the big problem that we are up against is that the modern textbooks are pushing these mathematical transformation equations in a way which disguises a very important difference between two completely different situations. These two different situations are described in the famous Bucket argument.

My natural inclination would be to view centrifugal force as a convective force. In other words it is a force which comes into existence at right angles to the direction of motion of a particle moving in a curved path. And that the effects, which are now described to be real, in the introduction are only effects which have come into existence BECAUSE the object is engaged in a curved path motion.

At the moment, the introduction is now admitting to real effects. It was never actually an issue in the edit war about whether or not these real effects could be explained in different ways in different frames.

Initially, I was arguing against a party which were adamant that these effects were entirely fictitious and could only be viewed in the rotating frame.

Finally by pushing the issue of the centrifuge which clearly disproves such a fictitious outlook, the reality of these effects was finally acknowledged. However, in a sense it is being whitewashed by pointing out that centrifugal force is a fictitious force by virtue of the fact that it is merely an appropriate way of describing effects in a rotating frame which could be described by other means in the inertial frame.

This is an improvement. But it still lacks the most important clause of all.

That clause is that centrifugal force is about real radial effects which come about BECAUSE of curved path motion.

Unfortunately the interpretation of the maths that these guys are pushing is indeed the official line. I did it myself many years ago in applied maths and I can confirm that.

The maths itself is correct. But they are interpretating it such as that ω^2r means that the centrifugal force acts on any body in a rotating frame.

I am adamant that the ω term is telling us that it only applies to objects that themselves have that ω. And the fact that a centrifuge only works for co-rotation would tend to back that idea up.

It would seem however that what they are preaching is indeed what is being preached in the universities.

So there's not really very much that anybody can do to help the situation. The first line in the introduction messes it all up from the outset.

I would have liked a line that drew attention to the absolute reality of co-rotation situations. That is essentially what the recent stage of the edit war was about.

But at the end of the day, there is no doubt that fictitiousism is in the ascendency at the moment.

I have just heard that sometime in the early 1950's the textbooks on orbital theory switched the centrifugal force term in the equations into centripetal force.

So really the problem is too far gone now for anybody to be able to do anything about it. David Tombe (talk) 17:53, 3 May 2008 (UTC)

Cartesian coordinates

Brews, in Cartesian coordinates, the centripetal force shows out alone as you say. I am totally familiar with the derivation. We take two velocity vectors on the arc of the circle and make a vector triangle. This leads to an inward pointing acceleration of value v^2/r.

But you are overlooking something very important. This centripetal acceleration is with reference to the straight line path that would have occured had the centripetal acceleration not been there.

This straight line path is in fact inertia. Now do that exact same vector triangle again using the straight line path referenced to the exact same point. This time you will get an outward acceleration of v^2/r. In other words, the centrifugal force is implicit in the inertia.

In polar coordinates, we only consider the radial direction, and in that case inertia becomes centrifugal force.David Tombe (talk) 06:25, 3 May 2008 (UTC)

Hi David: Well, knowing your interest in history, I think you're pulling my leg, and setting up to embroil me in the same controversies that prevailed in the 16th and 17th centuries. I'm sure it is amusing to see put into practice the old saw: "Those who cannot remember the past, are condemned to repeat it". Brews ohare (talk) 14:23, 3 May 2008 (UTC)

Brew's, if you can derive centripetal force, just repeat that derivation, but this time instead of considering the velocity vector as having changed its direction in relation to the Cartesian frame, consider it to have changed its direction outwards in relation to the radial vector. You will get exactly the same expression outwards and it applies to straight line motion in the Cartesian frame. Inertia IS centrifugal force.

There is another way of looking at it. Consider the general central force orbital equation. Gravity and centrifugal force combined yield a conic section. In the extreme case of when the gravity is negligible, we get a highly eccentric hyperbola. This is effectively a straight line.

In other words, centrifugal force acting alone leads to a straight line.

Centrifugal force in conjunction with centripetal force leads to a circular motion.

Conclusion. Centrifugal force is always there in the outward radial direction in circular motion, but in the Cartesian frame it is masked as 'inertia'.David Tombe (talk) 15:12, 3 May 2008 (UTC)

Hi David: The vector-based analysis of centripetal force uses the basic definition of change of displacement r( t + dt ) − r( t ) = ds, which is independent of any coordinate system. There is no issue to consider about "relative to the radial vector" or "in relation to the Cartesian frame". The vector ds exists in space as determined by the path r ( t ) and nothing else. It appears to me that all your verbal arguments simply collapse in the face of this extremely fundamental kinematic argument, which transcends all such considerations. Brews ohare (talk) 15:59, 3 May 2008 (UTC)

No Brews, let's consider the case when there is no centripetal acceleration and the particle moves in a straight line.

Now do that same vector triangle again referenced from the centre of that same circle that you would have used if there had been centripetal force.

This time you will discover a net outward direction changing acceleration.

In other words, the centrifugal force is there all along but disguised in the straight line motion which is inertia. It doesn't show up in the Cartesian analysis. But it is there.

Now go into polar coordinates and if we have circular motion, the centripetal force inwards will be exactly balanced by a centrifugal force outwards.

Consider an elliptical orbit. Consider the stage when the object is closing in on the centre. According to you this closing in is a consequence purely of the one and only inward acting centripetal force. And based on the expression for gravity (inverse square law), you might think that the fact that the gravity is getting stronger as it gets closer, would mean that it should spiral in even more so.

But it doesn't. At some stage of the orbit, it starts to go up again. What is that radially outward force that suddenly overcomes gravity?David Tombe (talk) 17:28, 3 May 2008 (UTC)

David: I am sorry, but you are dead wrong on this one. If the path is a straight line, the kinematical argument predicts zero acceleration. The kinematical argument outlined in the earlier comment and used in centripetal force simply does not use "triangles" or "Cartesian coordinates". Brews ohare (talk) 18:26, 3 May 2008 (UTC)

Brews, if we treat the straight line path from a Cartesian perspective, then the acceleration is zero if it has constant speed.

But if we treat it as measured radially from a fixed point, then it reads a centrifugal acceleration outwards of v^2/r.

Imagine an object going in a straight line with constant speed in the Cartesian frame. Imagine a lamp post which is not on its path.

At some stage the object will be getting progressively closer to that lamp post. Then a point of nearest distance will be reached and the object will then begin to get further away. If we consider the distance between the object and the lamp post, the second time derivative of that distance will be v^2/r away from the lamp post, where v is the component of the actual speed that is perpendicular to the radial vector. In other words, the maximum centrifugal force will occur at the point of nearest approach.

This is a central force orbit. The lamp post exerts negligible gravity and so the solution is a highly eccentric hyperbola which is efectively a straight line.

That is inertia and it is centrifugal force too.David Tombe (talk) 18:46, 3 May 2008 (UTC)

I'd suggest that you're doing some math in your head and making errors. If you actually put it on paper, you'll find that a straight-line motion as seen from the lamp post requires zero acceleration, even if the object does a near miss. To support this view, I can measure distance from the lamp post to the object as r ( t ). Then, for straight-line motion, at another time Δt later, r ( t + Δt ) = r ( t ) + v Δt. Hence, dr / dt = v. And if v is constant, a = dv / dt = 0 . Nothing here depends on where r is measured from. No use is made of any coordinate system. Brews ohare (talk) 19:14, 3 May 2008 (UTC)

Brews, in the scenario that I have given you, the direction of the position vector will be constantly changing and so it will be accelerating when viewed in that coordinate system. David Tombe (talk) 06:16, 4 May 2008 (UTC)

David: Math can greatly cut down on verbiage and contradictory assumptions. In this case, for example, r ( t ) = r ( t₀ ) + v•( t − t₀ ) shows clearly that r changes direction because the time-dependent vector v•( t − t₀ ) is added to it, changing its direction as time increases. However, the velocity associated with r ( t ) is v, and v is constant in magnitude and direction , so a = dv / dt = 0.

Again, no coordinate system is used in this discussion, and analysis in any coordinate system will agree with these results. Brews ohare (talk) 15:19, 4 May 2008 (UTC)

Reply to Wolfkeeper on Orbital Theory

Wolfkeeper, if you have failed to see the link between Kepler's law of areal velocity and the "2 times r dot theta dot" term in the tangential component, which is Coriolis acceleration, then it would appear that you really do have some fundamental misunderstandings of this topic. There is no angular acceleration involved in central force orbital theory.

While you are attempting to back up Steve and FyzixFighter, you are actually saying things that contradict them.

I suggest that the three of you get together to appoint a spokesman so that you can speak with a united voice and we can then bring this argument to a definite conclusion. David Tombe (talk) 09:54, 3 May 2008 (UTC)

The Whitewash Line

Plvekamp, this is what I mean by the whitewash. This line here sums it all up,

The results obtained by considering these pseudo-forces to be "real" within the rotating frame are identical to those given by calculations made in the inertial frame without them.

That line totally fails to address the fact that the most important aspects of centrifugal force, such as getting thrown to the side door of a swerving car, actually arise BECAUSE of the rotation.

The whitewash line evades that issue totally and acts as if we have these effects that just happen to be going on and we have different ways of describing them in different frames of reference. It misses the entire point of what centrifugal force is about in the name of trying to reconcile two conflicting viewpoints over whether centrifugal force is real or fictitious.David Tombe (talk) 18:04, 3 May 2008 (UTC)

Hi David: Maybe the problem here is semantical. The person thrown against the door sees "real" effects, maybe even has to visit the hospital. But these results are described differently in the inertial frame: the car turned but the passenger didn't. On an icy road, when the tires don't work, it's a "real" accident, but its because the driver did nothing "real" by turning the steering - the car went straight, the road turned. The use of "real" here in ordinary language is ambiguous. Brews ohare (talk) 18:53, 3 May 2008 (UTC)

Brews, the problem here is that any real effects only occur when the object co-rotates with the rotating frame and this fact is being suppressed. The passenger in the car is made to co-rotate by the back of his seat. A mutually perpendicular deflection is then induced which throws him to the side door. (vXω)

There are patterns of real cutting of lines of force here which are mirrored in electromagnetic induction. These are being ignored. The dominating 'Fictitious Party' here are trying to insinuate that the effect would be the same for a stationary object that is not co-rotating. No it wouldn't be the same. No forces will act on the stationary object. It is the Faraday paradox.

A spinning bucket of water induces a hydrosatic pressure. But no real effect is ever induced on a stationary object merely by viewing it from a rotating frame of reference.

At the moment, I can see that your big problem is that you haven't yet realized that polar coordinates are the only viable way to analyze these issues. Cartesian coordinates are useless for the purposes because they don't match the underlying reality. No matter how hard you try to analyze it all in Cartesian coordinates, you will still end up talking about the radial direction.

The polar system is the system that yields the clues about the underlying reality behind it all.

You try and see if you can successfully put any mention of actual radial acceleration into the introduction.

At the moment the bottom line of the introduction is effectively saying "If you came here to read about centrifugal force, you have come to the wrong page". David Tombe (talk) 04:24, 4 May 2008 (UTC)

This would not have been a problem if the article had not defined the centrifugal farce as fictious. So you need to say real, to distinguish it from fictious. Fictious means not real or imaginary. Pseudo means false. The confusion is on the part of the people who use these terms to discuss physics. I say again that the editors, and this means Mr Anemone, you dont understand physics, and this article on the centrifugal farce should be deleted from wikipedia since you will never get the physics right in this discussion.72.84.70.6 (talk) 20:28, 3 May 2008 (UTC)

As numerous independent contributors to this thread have pointed out, we use this term in the article simply because "fictitious force" is the standard usage and terminology for things like centrifugal force. This is because from the viewpoint of an inertial frame, generally chosen by physicists for the simplicity of its equations of motion, it does not exist. I personally prefer the less confusing term "pseudo-force", following Feynman, but ultimately it means the same thing. The universe does indeed "[act] as if we have these effects that just happen to be going on and we have different ways of describing them in different frames of reference", something which can not only be confirmed theoretically by transforming equations, but has also been demonstrated in practice in thousands of engineering applications involving rotational motion that have been constructed using these theories.

You are perfectly at liberty to use rotating coordinates and perform calculations using it, and call it a real force; your equations of motion will still describe the same universe as the simpler equations set in the inertial frame. You can even measure it with instruments within the rotating frame, and it will appear to behave exactly as you predict: this is a consequence of the equivalence principle. Nevertheless, your viewpoint, if not your terminology, will remain perfectly compatible with the simpler inertial frame treatment which treats this "force" as the mere result of the effect of coordinate transformations on the laws of classical mechanics as formulated in an inertial frame; and as a result, everyone else will also remain at liberty to continue to regard centrifugal force as nonexistent within the context of that system.

If you want this practice changed, you will first need to change the standard treatment of classical mechanics and the working practices of professional physicists and physics educators, and once you have done that, we can change the article to fit your tastes. Please read the essay at WP:TRUTH, if you have not done so already. -- The Anome (talk) 22:24, 3 May 2008 (UTC)

Anome, You've missed the point entirely. Centrifugal force is an effect which comes about BECAUSE of rotational motion. Spin an object and a centrifugal pressue will be induced.

It has got nothing to do with how we describe it in different frames of reference.

At the moment, the article begins by stating that centrifugal force is fictitious and that it is only apparent in rotating frames.

The article then continues by contradicting this and stating that there are real effects but that they would be there anyway whether there is rotation or not. Wrong.

The article then mentions that the centrifugal force that involves actual outward motion, which would be what people have in mind when they look up an article on centrifugal force, is not the centrifugal force that is dealt with in this article.

And it finally ends by stating that the whole matter is very confusing.

Anybody reading this introduction would simply say 'what?'. And they would be less wise about centrifugal force than before they read it.

I'm going to put in a qualifying clause regarding the necessity of the real effects to be induced by rotation. If this clause is deleted, which I am sure it will be, then I can only conclude that the person who deletes it has got absolutely no comprehension of the topic whatsoever.

In fact if I had been the one that had put in what you put in, it would have been deleted already because these people are not even happy with the idea of real effects at all.

But when it was deleted, somebody who would have deleted it if I had been the author, actually restored it.

It is clear from observing the activities on this page, that there is a certain group who revert according to who made the edit, rather than what the edit involved.David Tombe (talk) 03:47, 4 May 2008 (UTC)

David, the problem appears to be with the term "fictitious force". I don't think it's a great term, but that's what people have called it. I prefer the term inertial force. I find the article is perfectly clear and straightforward, but there is no way around wrapping your mind around the concept of an "apparent force" here. You seem to be confusing a rotating body (which is very real, and has of course real, not "ficticious" effects), and rotating coordinate systems which may be chosen at will. Edit-warring on Wikipedia is not a recommended way of getting to grips with elementary physics. Most people achieve that in the traditional way of picking up a book or visiting a school. dab (𒁳) 17:44, 4 May 2008 (UTC)

No Dbachmann, the problem is that you don't seem to realize that nothing actually happens at all unless there is very real rotation. That nmeans co-rotation in the rotating frame. You will notice that any attempts on my part to emphasize that fact, are systematically deleted. If you think otherwise, then please tell me all about the physical effects which are felt by a stationary object that is observed from a rotating frame of reference. David Tombe (talk) 09:09, 5 May 2008 (UTC)

Careful here, yet again. If a body is moving inertially- in a straight line, when viewed from a rotating frame of reference there is very evidently both a centrifugal force as well as a Coriolis force. There is no need at all for any real rotation to be present, all that is necessary is to do the relevant coordinate transformation, and it appears.- (User) WolfKeeper (Talk) 13:13, 5 May 2008 (UTC)

No Wolfkeeper, the Coriolis force does not occur in the natural state of affairs, but the centrifugal force does. This is a direct consequence of Kepler's law of areal velocity which eliminates the Coriolis force and the Euler force from planetary orbital motion. Everyday straight line motion is a special case of planetary orbital motion.David Tombe (talk) 15:43, 5 May 2008 (UTC)

Consider somebody standing in a rotating space station (e.g. O'Neill cylinder). Because it is spinning the convenient frame of reference is the rotating reference frame that rotates with the station. You're standing there, and you let go of a ball. Due to centrifugal effect, the ball falls to the ground. OK? Now, look at this from the external, stationary frame of reference, you've got this guy spinning around with the station, but his feet are going at a faster linear velocity than his hand (because the hand is nearer the rotation axis). So when he lets go of the ball, it is going to move (in a straight line, with constant speed, due to inertia, in the non rotating frame.) But if the feet are going faster, then they will be ahead of the ball when it lands- they are going faster at each and every point, and their angular velocity is higher at each and every point. So the ball lands behind. In the rotating frame of reference it looks like a magic force has pushed the ball backwards. (If that isn't obvious, take a simple example, and calculate how long the ball takes to hit the ground in the non rotating frame, and how far the feet have moved- I can do the calculation if it's too hard for you.) My questions is, what's the name of that magic force that pushes the ball backwards when you drop it in the space station, David? It's not centrifugal force, because that acts strictly outwards. And it's not Kepler's areal law, because there's no significant gravity.- (User) WolfKeeper (Talk) 16:21, 5 May 2008 (UTC)

I'm still waiting for an answer David.- (User) WolfKeeper (Talk) 04:39, 7 May 2008 (UTC)

The problem with inertial force is that it sounds like a real force. I prefer fictitious myself. Or pseudoforce perhaps, but I'm not sure about that. --Doug Weller (talk) 18:02, 4 May 2008 (UTC)

well, it is a "real force" in a way. The point is, forces are something "real" (i.e., they don't just appear for no reason). That's unless you choose a non-inertial coordinate system. But in real life you'll only ever do that if something is moving along non-inertial lines, which means that there are forces present. Be aware that I am not discussing the physics here, which I understand, but the presentation to somebody who doesn't yet understand it. David is confused because we tell him a force is "fictitious" which has a real effect. That's because he keeps imagining items (cars, water buckets) that do experience some force, and the choice of coordinate system does only follow suit. Nobody will ever choose a rotating coordinate system if there isn't some rotating body involved. This is imho the origin of the confusion. The confusion is all David's, of course, and he has no business disrupting the article, but I am addressing the question as if he had asked politely on WP:RD/S where misunderstandings such as this one would properly belong. dab (𒁳) 18:24, 4 May 2008 (UTC)

Dbachmann, the confusion is not all mine. The confusion is all yours for failing to be able to see that actual rotation induces real radial effects, whereas no effects at all are induced on a stationary object whether it is observed from a rotating frame of reference or not.David Tombe (talk) 09:18, 5 May 2008 (UTC)

A little different way of looking at people's positions is to divide them into the "theorists" for whom inertial frames are "it", and "experimentalists" who aren't interested in formalism, but in what they actually experience. If you love pure thought you can tell the man slammed against the subway door that in a different world (an inertial frame) he got smashed by a fictitious force, but he is likely to tell you where to put your inertial frame: he is living in this frame. Brews ohare (talk) 18:38, 4 May 2008 (UTC)

my point is: the man being slammed against the door isn't experiencing a "fictitious" force, he is experiencing a force that has a real physical cause. The "fiction" part is just that it appears the force is acting on him while it is in fact acting on the subway train. dab (𒁳) 19:35, 4 May 2008 (UTC)

Does it only appear that his bones are broken?119.42.68.141 (talk) 10:09, 9 May 2008 (UTC)

Definition of Centrifugal force

From the McGraw Hill Dictionary of Mathematics and Physics centrifugal force: (1) An outward pseudo-force, in a reference frame that is rotating with respect to an inertial reference frame, (2) The reaction force to a centripetal force. —Preceding unsigned comment added by Denveron (talk • contribs) 04:48, 4 May 2008 (UTC)

One of the requirements of scientific thinking is that the terms used in science have a definite and clear meaning and that there is an economy of terms used. This is not the case in modern physics which has multiplied a profusion of confusing and ambigous terms to discuss centrifugal force. There was no problem with this definition for several hundred years. Yet now, one can not read a physics book without being subjected to a multitude of ambigous confusing and absurd definitions that basically are meaningless metaphysical entities which contribute nothing to the understanding of the physics involved. The fact that wikipedia can not make sense out of this centrifugal farce demonstrates the useless aspect of these absurd terms. Wikipedia editors dont know what these terms mean and they cant explain them here, so you should call this article the centrifugal farce. The article should be entirely deleted since you will never get it right.72.84.66.108 (talk) 15:04, 4 May 2008 (UTC)

People have been wrong about many things for enormous lengths of time; further, life was arguably much simpler in the past. That is not an argument for keeping outdated and incorrect ideas, particularly not in the name of "scientific thinking". ETA I think that the second definition above is perfectly clear and straightforward, and could be used as the basis for simplifying and clarifying the introduction. Most readers are not going to want to read anything about reference frames—rotating, intertial or otherwise. SHEFFIELDSTEEL^TALK 17:35, 4 May 2008 (UTC).

Sheffield Steel, I have been advocating that very point. There is no need to mention rotating frames of reference at all. It merely provides a mechanism within which to perform conjuring tricks with the maths. It obscures the underlying reality of the fact that centrifugal force only occurs when actual curved path motion happens.

In relation to your reply to 72.84.66.108, can you please tell us all exactly what outdated and incorrect ideas you have in mind. From what I can see, he is saying the same as me, which is that we need to have co-rotation in order for centrifugal force to occur. Is that an outdated and incorrect idea?David Tombe (talk) 09:15, 5 May 2008 (UTC)

Yeah, actually.- (User) WolfKeeper (Talk) 14:26, 5 May 2008 (UTC)

A different intro

What I got from the above pages of chatter was that the Introduction was too geeky - not everybody is a mathematical aficionado. So to please David and provide a bit broader attack on the subject than "coordinate transformations" I rewrote the first few paragraphs. I know it's presumptuous of me, but somebody said it's easier to revise something than to look at a blank page. So go for it. Brews ohare (talk) 06:19, 4 May 2008 (UTC)

Brews, You mention about these 'real physical effects'. Then you erased my reference to co-rotation. Can you please tell me which real physical effects, that aren't co-rotating, are best described from a rotating frame of reference? What 'real physical effects' have you got in mind?

Are you seriously trying to tell me that a stationary bucket sitting on the ground is best described from the perspective of a rotating frame of reference?

I think that you will soon realize why I inserted that clause into your revised introduction. This is the key point in the whole dispute. What I am currently arguing with Steve and FyzixFighter about now is only a secondary issue.

On that other point about centrifugal force being inherent in straight line motion past a lamp post, imagine the traffic police standing at the lamp post and pointing their speed radar gun at the oncoming object.

Now remember, the object, let's say a car, is driving at a constant speed in a straight line Cartesianly. It is coming from a distance and it passes the lamp post at a nearest distance of 50 yards.

Will the radar gun register the same speed the whole time?David Tombe (talk) 08:44, 4 May 2008 (UTC)

David: the intro is not a place to throw in a "co-rotating" reference, which cannot help being confusing as an inserted parenthetic aside in a sentence of general nature. If this topic is central, it needs specific discussion with examples in a separate sub-section later on. Insertion of only a few words mid-sentence may avoid careful scrutiny, but it will not explain the subject.

I'll reply to the centrifugal force discussion in the earlier segment.Brews ohare (talk) 15:06, 4 May 2008 (UTC)

In response to your repeated attempts to insert a "co-rotating objects" reference; what exactly does that add to the meaning of the sentence? Do you regard it as a clarification? I think it is a confusing limitation upon the general argument of the sentence. Brews ohare (talk) 15:38, 4 May 2008 (UTC)

You must be joking. The entire article is a morass of confusion, and you are complaining about a small attempt at clarification. The article is nonsense as it stands and the attempts to sort out the confusion by imposing more rigorously defined nonsense is a joke. 72.84.66.108 (talk) 16:52, 4 May 2008 (UTC)

Confusion and misconceptions

This subsection should be deleted. What is not a rant is either repetitious or unsupported. Brews ohare (talk) 16:04, 4 May 2008 (UTC)

Deleted. I've created a new section to address the matter of whether centrifugal force is "real". -- The Anome (talk) 16:57, 4 May 2008 (UTC)

I think we may need to cover centrifugal effect, and then extend it to cover centrifugal force. There's no other article on centrifugal effect per se.- (User) WolfKeeper (Talk) 00:00, 5 May 2008 (UTC)

As in this treatment? That seems like a really good plan. -- The Anome (talk) 00:29, 5 May 2008 (UTC)

Centrifugal Force only occurs with actual curved path motion

'Rotating frames of reference' only clouds the entire issue. The key point which is being consistently swept under the carpet is the fact that the transformation equations only apply to co-rotating objects. If there is no co-rotation, then nothing happens.

It is clear that this entire mess is a result of total denial of this fact. I have looked through the edits of the last day and I can see that Virginia anonymous has been trying to push this same point, but that just as when I do it, it gets deleted immediately.

It seems to me that it is much more important to all of you to emphasize trivial facts, such as 'These real effects can also be described equally well in an inertial frame', than to mention the most important fact of all which is that these real effects are actually induced by the rotation itself.

Recently we saw the parent force for both the centrifugal force and the Coriolis force. It takes the form vXω.

The manner in which the editors here have been trying to present this very real inductive effect would be analgous to trying to explain electromagnetic induction as follows,

As viewed from the frame of reference of a rotating bar magnet, an electric current is seen to be induced in a nearby electric circuit. This effect can be equally well described from the inertial frame.

I'm sure that you would all agree with me that it would be the height of nonsense to explain electromagnetic induction like that because it misses out on the most crucial aspect of all which is that the induced electric current occurs BECAUSE the bar magnet is rotating.

Um. LOL. You do know that electromagnetism forms a 4-vector, and due to Lorentz coordinate transformation magnetism and electic fields can convert into one another in moving frames of reference, and that this is considered to be a form of rotation (in a hyperbolic geometry)? In other words, its pretty similar...- (User) WolfKeeper (Talk) 13:19, 5 May 2008 (UTC)

You are all doing exactly the same in this article. You are all denying the underlying induction aspect that is caused by absolute rotation.

So if you guys are going to insist on deleting all references to the importance of co-rotation, then you will all remain confused for a very long time. David Tombe (talk) 08:58, 5 May 2008 (UTC)

LOL. No, it happens with inertial paths, stationary objects, curved paths, things that are spinning around the frames' axis, things that are spinning about a different axis, things that are spinning at a different rate about the same or different axis, or variable axis... It occurs to everything that isn't on the frames rotation axis...- (User) WolfKeeper (Talk) 13:17, 5 May 2008 (UTC)

No Wolfkeeper, it doesn't. A stationary object in the inertial frame experiences no physical effects by virtue of being observed from a rotating frame. David Tombe (talk) 15:19, 5 May 2008 (UTC)

The need for references

I notice that there is now a section entitled 'Is centrifugal Force Real?'.

Well at the beginning of the edit war, I mentioned that Newton, Maxwell, and Bernoulli had believed it to be real. I even provided references. But that true fact was instantly deleted. The 'Fictitious party' are not even comfortable with any mention of the fact that centrifugal force was once believed to be real by the great masters of physics.

You can read this interchange with PeR at the beginning of the edit war and make up your own minds,

David, The centrifugal force was never considered to be real by Newton, Maxwell, or Bernoulli. If you want to put a statement like that you need to cite a source. Specifically you need to cite a source that says "the centrifugal force was considered to be real", or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 17:16, 20 April 2008 (UTC)

Reply: Admissibility of Evidence

PeR, I think that you are going to have to repeat yourself. We need to get something straight here regarding the issue of admissibility of evidence. You declared that centrifugal force was never considered to be real. You further went on to state that if I were to produce any quotes from Newton or Bernoulli which indicated that they believed that centrifugal force was real, that this would not be deemed to be admissible evidence on the grounds that it would be my own original research. Here is a quote from Bernoulli out of the ET Whittaker book on the history of aethers.

"The elasticity which the Aether appears to possess, and in virtue of which it is able to transmit vibrations, is really due to the presence of these whirlpools; for, owing to centrifugal force, each whirlpool is continually striving to dilate, and so presses against the neighbouring whirlpools."

And here is a quote from Maxwell's paper 'On Physical Lines of Force',

"The explanation which most readily occurs to the mind is that the excess of pressure in the equatorial direction arises from the centrifugal force of vortices or eddies in the medium having their axes in directions parallel to the lines of force"

And you are trying to tell me that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real?

YES! I am trying to tell you that this is not evidence to suggest that Bernoulli and Maxwell believed that centrifugal force was real. However, if you don't want to accept this you don't have to. Just don't write anything in the article. If you do want to write something like that then you must (and here I am repeating myself, as requested) cite a source that says "the centrifugal force was considered to be real" or something very similar to that. If you read a text by, say Maxwell, and interpret that as him saying that the centrifugal force is real, that is still original research, since it is your interpretation of what he says. --PeR (talk) 19:42, 21 April 2008 (UTC)

reply: PeR, There is a controversy about whether or not centrifugal force is real. The official position today is that it is not real. The current introduction is abominable because it tries to fudge the issue by pretending that there are two centrifugal forces. One for the realists, and one for the fictitiousists. This is an extreme case of ecclecticism. The current introduction cannot remain because it is a total disgrace.David Tombe (talk) 08:02, 21 April 2008 (UTC)

He replies. You misinterpret what it says. However, the fact that you don't understand it is evidence that it is not clearly enough written, so I agree that it should be rewritten. --PeR (talk) 19:42, 21 April 2008 (UTC)

David Tombe (talk) 09:33, 5 May 2008 (UTC)

So Maxwell and Bernoulli mention centrifugal force in their papers. That's a bit of a non-sequitor. Physicists today also mention centrifugal force in their papers. Can you find a quote from M or B in which they talk about the character of centrifugal force, instead of a side mention ? These two quotes don't address the issue. Plvekamp (talk) 13:21, 5 May 2008 (UTC)

Yes I could dig up alot more on the subject. Maxwell uses centrifugal force to explain magnetic repulsion. Read his whole 1861 paper. But we don't need to go into that here.

Those quotes which you deleted simply drew attention to the fact that Maxwell and Bernoulli believed centrifugal force to be real. The section was entitled 'Is centrifugal force real?' and so I was letting the readers know what Maxwell and Bernoulli thought. What exactly is your problem with this kind of information? David Tombe (talk) 15:48, 5 May 2008 (UTC)

Simply because they use the concept, doesn't mean they interpreted it the same way you do. Modern physicists also use the concept, yet disagree with your interpretation. You need to show a quote that shows that their interpretation agrees with yours. Those two mentions don't give any more information than that they were familiar with the concept, and used it in their theories. Plvekamp (talk) 16:35, 5 May 2008 (UTC)

David: This discussion is all a bit silly. The article already says that "fictitious" has the meaning "unnecessary in an inertial frame of reference". Would you argue against that as a definition? As a fact, so far as centrifugal force is concerned?

The article also says that centrifugal force is a very real effect in a non-inertial frame. What exactly are you trying to accomplish here? Brews ohare (talk) 14:14, 5 May 2008 (UTC)

Brews, when actual co-rotation occurs, the centrifugal force is (1) real, (2) radial, and (3) it can be observed from all reference frames. It is an absolute effect.

When there is no co-rotation, then there is nothing. There is no centrifugal force. There are no physical effects in any reference frame.David Tombe (talk) 15:17, 5 May 2008 (UTC)

David, Just to clarify what I meant, above. (If you didn't read WP:OR and WP:V the last times you were asked to, then please do it now.) If you were to state "Maxwell mentions a 'centrifugal force'", then the above citation would be sufficient. But if you want to say that he believed that it is real, then you'd need a statement by Maxwell along the lines of "I believe that the centrifugal force, which others say is fictitious, is actually real", or a statement by some authority on science history asserting what Maxwell thought. From what you quote, the reader has no way of knowing whether Maxwell is referring to the term used in this article, or if he is using it in its literal sense to mean any "force that is directed away from the center". Hope this helps. --PeR (talk) 20:45, 5 May 2008 (UTC)

PS. Maxwell was considered a genius of his time. If he was wrong on a matter of elementary physics that would be a widely published fact, so you wouldn't have a hard time finding a reference. For comparison see how easy it is to find reliable sources asserting that Einstein said that [God] does not play dice. --PeR

The swerving car

Timothy, this is a reply to,

David, when your talking about what "a person sit in a car driving in a circle" experiences, you are implicitly specifying a frame of reference. Namely, what a person experiences can only be described in a co-moving frame. Such a frame is typically non-inertial and will thus contain psuedoforces (or however one wishes to call them) from the perspective of this observer/person these forces are very much real. As you state the person feels himself pushed towards the outward door. An other observer will understand this diffently. An observer from an inertial frame will see the person in the car being forced to move in a circle by force exerted on him by the car.(TimothyRias (talk) 14:32, 5 May 2008 (UTC))

You have got completely confused between (1) the force that causes the co-rotation ie. the pressure on the man's back from the seat of the car, which is in the tangential direction, and (2) the centrifugal force which is induced by this co-rotation and acts outwards in the radial direction causing him to slide to the side door.

The induced centrifugal force is (1) real, (2) radial, (3) and can be observed by everybody irrespective of what frame of reference they are in. In fact, there are no frames of reference. The centrifugal force is an absolute effect, associated with absolute rotation.David Tombe (talk) 15:27, 5 May 2008 (UTC)

What happens when there is no seat back? Same thing happens, he slides to the door. Thus your co-rotation argument here is a red herring. Plvekamp (talk) 16:59, 5 May 2008 (UTC)

If you want to argue from ancient references, please take a look at Newton's Principia Book 1 and Euler's Mechanica Chapter 5, in which curvilinear motion is discussed. Neither author finds it necessary to use centrifugal force; but centripetal force is ubiquitous. Why is that? (Clue: the analysis in both cases uses inertial frames of reference.) Additionally, why do modern physicists also mention centrifugal force in their articles, but yet, none of them here on Wikipedia agree with your interpretation? There must obviously be a cabal, since you have the WP:TRUTH. Plvekamp (talk) 15:49, 5 May 2008 (UTC)

Plvekamp, what ancient references are you talking about in realtion to my reply to Timothy Rias?David Tombe (talk) 15:57, 5 May 2008 (UTC)

Surely you're pulling my leg. The only references you've used, Maxwell and Bernoulli. Plvekamp (talk) 16:04, 5 May 2008 (UTC)

David, instead of just stating that people are completely confused, you might try and use actual arguments. Our at least try to understand other people's arguments. And actually the centrifugal force induced on the man in the car is only perceived in the co-moving frame. And observer in an inertial frame will only perceive one force acting on the man in the car and that is the force exerted on the man by the car. (well if you would also count gravity that would be two, but that is really beside the point) (TimothyRias (talk) 20:56, 5 May 2008 (UTC))

Timothy and Plvekamp, If the back seat of the car is not causing the man to move with the car, then something else will be. If nothing is causing the man to move with the car, then he will not be co-rotating and he will not experience any acceleration in the radial direction in the car's frame of reference. The Maxwell and Bernoulli references had got absolutely nothing to do with that point.David Tombe (talk) 07:32, 6 May 2008 (UTC)

David, you are missing my point. Sure the seat in the car is exerting a force on the person in the car causing him to follow its movements. My point was that if viewed from an inertial frame this is the only force acting on the man even when going around a corner. When the car is driving around in a circle at constant speed the force exerted on the man by the car is completely radially inward. (I'm neglecting gravity here for the moment for convenience of speech) (TimothyRias (talk) 07:48, 6 May 2008 (UTC))

Timothy, if a man was standing in the street watching the swerving car, he would see the back seat of the car pushing the passenger tangentially and he would see a radial centrifugal force induced that causes the passenger to slide outwards towards the side door.David Tombe (talk) 08:05, 6 May 2008 (UTC)

No David he would not! If what you say would be true, then the person on the street would see the person in the car make a curve in the opposite direction of the car. We all know this to be false, the person will move in a straight line as seen from the street. (TimothyRias (talk) 08:18, 6 May 2008 (UTC))

No Timothy, the person in the street sees the passenger move in a straight line in the Cartesian frame, but he also sees the passenger moving out radially towards the side door in the rotating frame. He can see both frames at once. David Tombe (talk) 08:44, 6 May 2008 (UTC)

David, you have convinced me. You have have absolutely no clue about physics whatsoever. You can only describe physics from one frame of reference at a time. Concepts like forces, energy, etc. are very much frame dependent and need conversion when translated frame on frame to an other. Sure the man on the street can describe the physics in the car using a co-rotating frame, in which case there is pseudo force present in the form of the centrifugal force. But, when he describes the physics from the his natural frame (ie the one that is comoving with his motion, ie an inertial frame) then no such force is present. (TimothyRias (talk) 09:17, 6 May 2008 (UTC))

Timothy, I was only describing it all in one frame at a time. The centrifugal force occurs radially when the passenger is subjected to a tangential motion. You can consider that effect real or fictictious. It's up to you. But one thing is sure. It only occurs when the passenger has a tangential velocity. It does not occur on objects that are not co-rotating with the car. David Tombe (talk) 13:32, 6 May 2008 (UTC)

Um, but the passenger is also pushed forwards by the seat in that scenario- this is because as the passenger slides outwards he meets the seat- and the seat is moving faster than he was. This causes the passenger to sink backwards in the seat cushions, because he is being accelerated as he slides. Or, easier to see, if he was sitting near the front of the seat and the seat is slippery, he would tend to slide backwards with respect to the car, for the same reason- the back of the seat is moving faster than him because it's on a wider curve, and traversing it in the same time as the rest of the car.- (User) WolfKeeper (Talk) 04:47, 7 May 2008 (UTC)

Really? What happens if a ball is flying over the car in the same direction and speed? That would follow exactly the same trajectory as the man in the car but just a couple of meters higher. (again neglecting gravity and any friction for the moment) (TimothyRias (talk) 14:10, 6 May 2008 (UTC))

Yes, Timothy. And the ball would also have centrifugal force in relation to the centre point of the car's circular motion. The actual factor that induces centrifugal force is 'tangential velocity relative to a point in space', and the centrifugal force is a radial force measured relative to that point.

Co-rotation in a rotating frame of reference is only one particular scenario that brings about centrifugal force. It is not the most general scenario. When I said above It does not occur on objects that are not co-rotating with the car., I was specifically referring to stationary objects. David Tombe (talk) 04:25, 7 May 2008 (UTC)

Corotation

This is copied from above:

--- Brews, when actual co-rotation occurs, the centrifugal force is (1) real, (2) radial, and (3) it can be observed from all reference frames. It is an absolute effect.

When there is no co-rotation, then there is nothing. There is no centrifugal force. There are no physical effects in any reference frame.David Tombe (talk) 15:17, 5 May 2008 (UTC)

David: Blanket assertions like this cannot carry your argument. To be persuasive, you'll have to get mathematical. For example, take a look at the derivation and point out what you think is at stake here in mathematical terms. Brews ohare (talk) 17:03, 5 May 2008 (UTC)

More to the point, to comply with Wikipedia's verifiability policy, it must be accompanied by a reference that states that this is the case: bold assertion is not enough. -- The Anome (talk) 17:56, 5 May 2008 (UTC)

Exactly what do you mean by 'co-rotation' then? Are you saying that both the rotational frame and the object have to be rotating at exactly the same angular rate and if they were moving 0.0000000001 radians per second differently, then there's no centrifugal force? So the surface of the Earth is not subject to centrifugal force due to the tiny difference in angular rate due to continental drift?- (User) WolfKeeper (Talk) 18:52, 5 May 2008 (UTC)

Wolfkeeper, You have changed the context. In my original discussion with Brews, I was saying that in straight line motion in the inertial frame, centrifugal force is built into that motion in the form of inertia. If we measure the second order time derivative of radial distance from a fixed point, we will get v^2/r where v is the component of the velocity that is perpendicular to the radial line.

You tried to cloud the issue by introducing Coriolis force. Coriolis force is not involved in that scenario. Kepler's laws have eliminated Coriolis force from planetary orbital theory.

You then went on to introduce a rotating frame of reference scenario which would indeed involve fictitious tangential effects. David Tombe (talk) 07:49, 6 May 2008 (UTC)

Brews, If something is not co-rotating, there will be no centrifugal force. What citations would I need to back up such a trivial point?

Imagine a long straight metal arm attached to a fulcrum and rotating in a horizontal plane one inch above the ground. Put a ball in its path. That ball will move out radially. That is centrifugal force.

Now repeat this expereiment with the long metal arm raised up ten feet. It will not touch the ball. The ball will not co-rotate and so it will just sit there still. There will be no centrifugal force on the acting on the ball.

Now the maths that you talk about suggests that there is actually a centrifugal force acting on the stationary ball but that it is over ridden by a Coriolis force twice as strong that acts radailly inwards.

Coriolis force never acts radially inwards. Coriolis force and centrifugal force both derive as mutually perpendicular components of a parent convective force vXω.

Those fictitious force equations are certainly correct when applied to the oceans and the atmosphere. But that's because the oceans and the atmosphere co-rotate with the Earth.

Those equations are only designed to deal with objects that are physically connected with the ω vector. You take a close look at the derivation of those equations and see if what I am saying is not true. David Tombe (talk) 07:49, 6 May 2008 (UTC)

Lets derive those equations shall we. Lets consider a particle ${\vec {x}}$ moving in a rotating frame rotation with angular speed ${\vec {\omega }}$. At any time the kinetic energy of this particle will be given by $T=1/2m({\dot {\vec {x}}}+{\vec {\omega }}\times {\vec {x}})^{2}$. The corresponding action is $S({\vec {x}})=\int T-V({\vec {x}})dt=\int \left(1/2m({\dot {\vec {x}}}+{\vec {\omega }}\times {\vec {x}})^{2}-V({\vec {x}})\right)dt$ By the action principle the variation of this should vanish

${\begin{aligned}0&=\delta S=S({\vec {x}}+\delta {\vec {x}})-S({\vec {x}})\\&=\int \left(1/2m({\dot {\vec {x}}}+{\dot {\delta {\vec {x}}}}+{\vec {\omega }}\times ({\vec {x}}+\delta {\vec {x}}))^{2}-V({\vec {x}}+\delta {\vec {x}})\right)dt-\int \left(1/2m({\dot {\vec {x}}}+{\vec {\omega }}\times {\vec {x}})^{2}-V({\vec {x}})\right)\\&=\int \left(m({\dot {\vec {x}}}\cdot {\dot {\delta }}{\vec {x}}+({\vec {\omega }}\times {\vec {x}})\cdot ({\vec {\omega }}\times \delta {\vec {x}})+{\dot {\vec {x}}}\cdot ({\vec {\omega }}\times \delta {\vec {x}})+{\dot {\delta }}{\vec {x}}\cdot ({\vec {\omega }}\times {\vec {x}}))+{\vec {F}}({\vec {x}})\cdot \delta {\vec {x}}\right)dt+O(\delta {\vec {x}}^{2})\\&=\int \left(m(-{\ddot {\vec {x}}}-{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {x}})-2{\vec {\omega }}\times {\dot {\vec {x}}})+{\vec {F}}({\vec {x}})\right)\cdot \delta {\vec {x}}dt+O(\delta {\vec {x}}^{2})\end{aligned}}$

This implies the equation of motion:

${\vec {F}}=m\left({\ddot {\vec {x}}}+{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {x}})+2{\vec {\omega }}\times {\dot {\vec {x}}}\right)$

which is equivalent to the transformation formula present in the article. From this derivation it is manifest that ${\dot {\vec {x}}}$ can take any vector value, and is independent of ${\vec {\omega }}$. In particular, ${\vec {v}}={\dot {\vec {x}}}-{\vec {\omega }}\times {\vec {x}}$ is not radial as you have been claiming. (TimothyRias (talk) 09:07, 6 May 2008 (UTC))

Timothy, $v={\dot {\vec {x}}}$ was radial right from your very first equation of kinetic energy. You split that equation into a radial and a tangential component in Pythagoras format. David Tombe (talk) 09:16, 6 May 2008 (UTC)

I did no such thing. I subtracted a vector and then took the norm. The vector I subtracted ${\vec {\omega }}\times {\vec {x}}$ has no relation with ${\dot {\vec {x}}}$ whatsoever, it is just a position based factor having to do with the fact that we are describing the physics in a rotating frame. Really, start listening to the people with actual degrees in physics that understand what they are talking about. (TimothyRias (talk) 09:26, 6 May 2008 (UTC))

Mr Rias, This seems to be original research. These equations need verification. Please cite your peer reviewed journal article reference and the textbooks that explain the source of your argument so that it can be checked to see if it is correct. You should know that citations are required by Wikipedia policy. Where are they? This argument can not be accepted as true until the citations are provided and the math is checked.72.64.40.44 (talk) 13:15, 6 May 2008 (UTC)

Argument is true by simple mathematical logic. There is nothing orgininal about this calculation. The basic principle, the action principle, is well established. Similar (equivalent) computations can be found in most textbooks on classical mechanics. Probably as an exercise in one of the sections on Lagrange formalism. (TimothyRias (talk) 14:05, 6 May 2008 (UTC))

It's true that one can't use math to prove an original point, when that point cannot be cited from a reliable source, when writing an article. This is a talk page, and math is a perfectly valid tool for giving an explanation to another user; and in any case, the conclusion of the calculation can be cited. -- SCZenz (talk) 14:11, 6 May 2008 (UTC)

And what's sauce for the goose is sauce for the gander. David Tombe (talk) 05:12, 7 May 2008 (UTC)

There is no sauce, and no gander. A conclusion of any kind from a talk page cannot be cited on any of wikipedia's articles.- (User) WolfKeeper (Talk) 06:08, 7 May 2008 (UTC)

Timothy, Yes, I see what you have done now. It is indeed an arbitrary velocity. But I can't see how you have linked that arbitrary velocity to the velocity term in the transformation equations. I simply don't follow your arguments above. There is absolutely no need to introduce that kind of mathematics to the problem. You are beginning at a very strange point. You begin with the general expression for kinetic energy for a particle in a rotating frame of reference. Correct. But then you introduce a potential energy term that is not needed. After a few manipulations which I simply don't follow, you conclude that it all implies the relevant transformation equations. You would need to show what all the maths terms mean at each stage of the derivation. Those same equations can be derived much more transparently in such a way that we can clearly see that the velocity term has to be the radial velocity. Why did you choose to introduce all that unnecessarily complicated maths above? There was absolutely no need for it. The point has been proved with a much more simple maths. So it can hardly be disproved just by introducing more complicated maths. David Tombe (talk) 13:25, 6 May 2008 (UTC)

The "complicated" maths you are referring to is simply varitional calculus, and it is not hard it is basic undergrad physics. it is just Lagrange formalism. It is the tool of choice when deriving equations of motion. Newtons laws serve the same purpose. (If you do the same thing for a particle in an inertial frame you just get Newtons second law. (which thus can be derived from the action principle!) The potential term is there to provide for other convention (conservative) forces (such EM or gravity) which added there own specific terms to the Lagrangian. You could also leave it out, but then you would the EoM for a free particle, i.e. the one without F, which would also be fine.

To me this one of the simplest ways to derive the EoM in a rotating frame. You haven't provided any "proof" of your statements. Here I have provide a simple proof that transparently disproves your claim. If this already goes above your head, you might want to reconsinder meddling in something that you clearly do not understand completely. (TimothyRias (talk) 14:05, 6 May 2008 (UTC))

Timothy, I've had a bit of time to think about your so-called proof. Your expression for kinetic energy is wrong because the velocity term is wrong.

The actual kinetic energy of the particle would pertain to its velocity as measured from the inertial frame. That velocity can be split into two components. One of those components is the velocity of the particle relative to the rotating frame. The other component is the velocity of the point that it is at in the rotating frame, measured relative to the inertial frame.

So we are back to the original argument. If we are going to use the expression ωXr for the latter, then it can only refer to the tangential velocity in the limit. It follows therefore that the other component must be the radial velocity.

Your expression for kinetic energy is wrong by virtue of the negative sign, and if you corrected it to a positive sign you immediately impose the restriction that the velocity term must be radial.

Regarding Hamiltonian mechanics, I did it in applied maths many years ago and it is totally unnecessary for the analysis of single particle motion where no potential energy is involved. Your error is present before your Hamiltonian maths even begins. There is absolutely no justification whatsoever for introducing Hamiltonian mechanics into a simple discussion about whether centrifugal force is induced on particles that are stationary in the inertial frame. David Tombe (talk) 04:15, 7 May 2008 (UTC)

Since ${\dot {\vec {x}}}$ is the velocity in the rotating frame, ${\dot {\vec {x}}}-{\vec {\omega }}\times {\vec {x}}$ is the velocity in the inertial frame. You're right it should be $1/2m({\dot {\vec {x}}}+{\vec {\omega }}\times {\vec {x}})^{2}$, I changed the derivation above to reflect this. In any case, whatever the relative sign, ${\dot {\vec {x}}}$ is independent of ${\vec {x}}$ so there is absolutely nothing forcing any one of the above expressions to be tangential. Sure, ${\vec {\omega }}\times {\vec {x}}$ is always tangential, that doesn't mean it is the tangential component of ${\dot {\vec {x}}}$.

And regarding Lagrangian formalism, it is the tool of choice in physics when in doubt what EoMs to use. It is very suitable to derive the EoM in a rotating frame. It is at least a lot less messy than trying to derive them directly from the coordinate transfromation. (which is also possible and gives exactly the same result. (TimothyRias (talk) 06:36, 7 May 2008 (UTC))

Timothy, Hamiltonian and Lagrangian have got nothing to do with it. Your error lies in your interpretation of the expression for kinetic energy. In fact you don't even need to involve kinetic energy. We only need to look at the particle velocity. The moment I see the ωXr expression, I can tell instantly that you have routed the velocity through a point on the rotating frame. ωXr is the tangential component of the particle velocity in the limit. And because it is in the limit, the other component must be radial. You cannot escape that fundamental reality which lies right at the heart of those transformation equations. What you did above was to cloud that reality up with a whole package of Hamiltonian, and integrals, and potential energies. David Tombe (talk) 09:43, 7 May 2008 (UTC)

What, limit? We are not taking any limit. There is no need to take a limit. ωXr is the tangential component of the particle only in the very specific case that the we choose the rotation of the frame of reference to be co-rotating with the particle. This is a very special case.

BTW, if you want a physical example of Coriolis forces acting radially you might want to look at the stability analysis of Lagrangian points. For example, without the contribution of the coriolis force, L1 en L2 would be radially unstable. The Coriolis contribution to the radial force stabilizes these points, allowing space ships to hover (or orbit) these points, a fact that is used effectively for many space missions. (TimothyRias (talk) 10:59, 7 May 2008 (UTC))

Timothy, the expression is absolutely dependent on it applying to the limit. If we consider the velocity vector split into two larger components, then none of those components are ωXr.

I repeat; what limit? (TimothyRias (talk) 12:54, 7 May 2008 (UTC))

On Coriolis force, it is not involved in Lagrange points or stability because there is no curl in the gravitational field. And in your books, it cannot be involved in stability because it is only a fictitious force.

FWIW coriolis force has absolutely no curl. If it had curl it would be a non conservative force. But it always acts at 90 degrees to the velocity vector and hence can't change the energy, and hence it's conservative (actually has no effect on the energy at all).- (User) WolfKeeper (Talk) 07:40, 8 May 2008 (UTC)

I never stated that. The effect of fictitious forces in non-inertial frames is very real. If it were not apples would not be falling from trees, since gravity is a fictitious force too! Anyway, it very simple if you remove the Coriolis force from the analysis of Lagrangian points no stable orbits are possible. This a simple fact anybody can do by doing the calculation/numerical simulation.(TimothyRias (talk) 12:54, 7 May 2008 (UTC))

This is another example of your tactic which is to move the discussion into unnecessarily complicated zones such as Lagrangian, Hamiltonian, and the three body problem which has never been satisfactorily resolved. It is actually a deceptive tactic used by alot of people who have been proved wrong in the simple arena. Move the debate into the dark dirty jungles and cloud the whole issue. David Tombe (talk) 11:46, 7 May 2008 (UTC)

First, you haven't proved anything, you have just made a bunch of blanket statements and provided no arguments. I've provided you with an argument, that apparently goes over your head, so you resort to accusing me of using dirty tricks.(TimothyRias (talk) 14:02, 7 May 2008 (UTC))

This argument can not be resolved because Mr Rias continues to claim his suspect proof, which has no verification, validation or corroboration, be accepted. It should rightly be rejected, because it proves nothing. The larger problem is that wikipedia continues to endorse an interpretation of physics that contradicts the classical textbooks written up to circa 1950. During the 1950s Sears and Zemansky introduced a different interpretation in their physics textbooks, and there is no proof that what they said is true. Apparently generations of students accepted what Sears and Zemanski said uncritically. It is now scientific dogma. I want to see the peer reviewed journal articles and committe reports that justify the revisionist interpretation that is the basis of what is claimed to be true by wikipedia editors. Where is the proof that what you say in the article is actually true? Where are the peer reviewed papers that prove this opinion, which you repeat here as truthful physics? I see citations to sources which are merely hearsay. I dont beleive hearsay. Where are the original peer reviewed journal papers that prove this is true?? Obviously one can only begin to decide the issue once they have been produced, since they obviously need to be analysed for errors before one can accept what they say is valid physics. So I again demand that you produce the poof that what you say in the article is valid physics and stop this nonsense.72.84.65.25 (talk) 13:50, 7 May 2008 (UTC)

It is a simple six line proof. I'm not saying you believe my word, you can just check the argument for yourself since it is all there. Anyway, up till now I have had very little to do with the actual content of the article except some rearranging and damage control. I've been focussing on trying to resolve the conflict on this talk page by introducing actual arguments. (TimothyRias (talk) 14:02, 7 May 2008 (UTC))

As pointed out above, nothing demonstrated on the talk page is relevant to the main article. So you have wasted your time. I want to see the peer reviewed proof that justifies the statements made in the main article. These need to be peer reviewed journal articles or reccomendations from a physics education committee and cited in the main page. As far I can determine, there is no peer reviewed, critically examined proof of what is said in the main article. Citations which refer to sources that repeat or draw conclusions from other unproved sources are not acceptable. I want to see the actual real proof, not hearsay that it exists in theory.72.84.65.25 (talk) 14:48, 7 May 2008 (UTC)

Timothy, your six line proof fails on the first line before you even reach all the fancy Hamiltonians, integral signs, and potential energy terms.

Your proof fails at the point where you assume that if one component of the particle velocity is ωXr, that the other component has got arbitrary direction. The much more basic and less pretentious vector calculus that is used to derive the term ωXr insists that this term only applies when it is the tangential component of the particle velocity in the limit that this component tends to zero. It is the very same calculus that is involved in differentiating the position vector to obtain the general acceleration equation in radial/polar coordinates. We differentiate r and we end up with ωXr in the tangential direction and r dot in the radial direction. Your big problem is that when you were first shown the derivation of the rotating frame of reference equations, you never questioned that detail. You just accepted what you were told. Now that you have seen that there are restrictions of applicability which you had never thought about before, you are just digging in because you entered this argument without first checking your facts. Hence you are trying to cloud the whole issue by introducing high powered maths topics like Hamiltonians, and Lagrangians, and best of all, the ever controversial three body problem. None of these complications are necessary in order to analyse a simple vector triangle of velocity for a simple one particle motion with no potential energy terms.David Tombe (talk) 15:58, 7 May 2008 (UTC)

OK, lets examine shall we:

• We fix a rotating frame with angular velocity ω.
• In this frame we describe the trajectory of a particle, starting a t=0.
• At this point we are free to choose any starting conditions. In particular we can choose the starting position x(0) and velocity v(0) of the particle.
• To obtain the speed in the inertial frame we need to add the velocity of the rotating frame at the starting position ωXx(0). That is v_inertial(0) = v(0) + ωXx(0).
• At this points you are concluding that this implies that ωXx(0) is the tangential component of v_inertial(0).
• Since we were free to choose ω, x(0) and v(0), we can clearly choose values such that this is the not case.

(TimothyRias (talk) 21:06, 7 May 2008 (UTC))

Timothy, no you cannot. You are free to choose whatever value of velocity you like. But if one of its components is described by the expression ωXr, then it must necessarily be the tangential component, and therefore the other component must be the radial component.David Tombe (talk) 06:34, 8 May 2008 (UTC)

Why? What is stopping us from having a velocity of, say,v_inertial(0) = 2 ωXx(0) such that v(0) = ωXx(0)? We are not making an orthogonal decomposition of the velocity. If we wanted we could decompose the velocity in a million non-zero components. Obviously, these would not all be linearly independent, but that is not a problem. (TimothyRias (talk) 07:19, 8 May 2008 (UTC))

Timothy, you can split the particle velocity into as many components as you like. But if one of those components is ωXr then the other component must be radial. This follows directly from the transport theorem. ωXr is the tangential component of the particle velocity in the limit. Hence the other component must be radial. You are ignoring a restriction that is built into the derivation. David Tombe (talk) 10:09, 8 May 2008 (UTC)

This is only true if you assume ω to be the angular velocity of the particle. We were free to choose ω independently of the velocity of the particle, so we can clearly choose ω not to be the angular velocity of the particle in which case ωXr cannot be the tangential part of the velocity. Your assertion basicly comes down to stating that there can only exist particles which are co-rotating with the frame. That is obviously false. (TimothyRias (talk) 12:23, 8 May 2008 (UTC))

No Timothy, it means that the equations only apply to particles that are co-rotating with the frame, because in those equations ω will represent both the angular velocity of the frame and the particle. If you choose ω not to be the angular velocity of the particle, then you cannot derive the transformation equations. There will be no physical linkage. v must be routed through the tangential term ωXr which is common to both the frame and the particle. 119.42.65.152 (talk) 13:30, 8 May 2008 (UTC)

Now, you are just talking in circles. There is absolutely no reason for any linkage between ω and the angular velocity of the particle. Moreover, if you assume no such connection, as I did, you find EoMs, that perfectly describe the kinematics of a (not necessarily co-rotating) particle in a rotating frame as can be perfectly checked. (and is used in all sorts of every day applications such as the calculation of space trajectories of satellites. —Preceding unsigned comment added by TimothyRias (talk • contribs) 07:36, 9 May 2008 (UTC)

The Orbital equation (2)

FyzixFighter, the orbital equation is found widely throughout applied maths textbooks. It takes the form,

-GM/r^2 + v^2/r = r double dot

It solves to give an ellipse, parabola, or hyperbola.

The inward -GM/r^2 term is the centripetal force. The outward v^2/r term is the centrifugal force. They both work together in the radial direction in tandem with each other.

I have been accused by two administrators of introducing unverified material by virtue of mentioning this information. That shows me that the editors that are dominating this page know very little about the subject matter. David Tombe (talk) 08:01, 6 May 2008 (UTC)

Yes, that is one way to write the orbital equation. However, it can also be written,

-GM/r^2 = r double dot - v^2/r

The only difference between this way and the way you wrote it is that I grouped all the (radial) acceleration terms on the right hand side. If applied math textbooks do write it the first way, then the question is what physical significance do they give the terms? By the way, what's a good applied math textbook that treats this problem as I would truly be interested to see how applied maths treat it? Back to the equation -

1) Since r double dot is not the radial acceleration, then

2) the left hand side is not the net force.

3) When the right hand side is made to be the radial acceleration (r double dot - r*(theta dot)^2) (and multiplied by the mass) then

4) we can call everything on the left hand side a force. When this is done for the orbital equation, the net force is found to be simply -GMm/r^2.

So where in this reasoning do we disagree, or rather, where does a reliable source disagree with this reasoning. --FyzixFighter (talk) 15:22, 6 May 2008 (UTC)

FyzixFighter, Let's leave names and terminologies out of it altogether. We have a second order time differential for the radial distance from the focus. Call it acceleration if you like, or don't call it acceleration if you don't like. That second order differential term is equated to two other terms. One is an inward acting GM/r^2 term. Call it gravity if you like. Don't call it gravity if you don't like. We also have an outward acting v^2/r term. Call it whatever name you like. But one thing is sure. Both of these terms are very real. They are both radial, and they both act in opposition to each other. That's what planetary orbital theory is all about. It could be correctly said that one of these terms is the centripetal force and the other is the centrifugal force. That second order differential equation is difficult to solve, but it has been tackled over the last couple of hundred years by the top applied mathematicians and there are a number of ways of solving it. I have seen at least two methods. The one that I actually had to learn for my exams involved substitution and we ended up with a new variable U. The derivation went for at least a couple of pages. Maybe even three or four pages. The final result is the geometrical expression for a conic section. There will be two arbitrary constants in that expression. One is the semi latus rectum and the other is the eccentricity. When we know the initial speed, position, and direction, we can work out what these two constants are and that tells us the exact shape of the conic section. If the eccentricity is less than 1 we will have an ellipse. A circle is a special case of the ellipse. If we have an eccentricity that is equal to 1, we get a parabola. In other words, the object has escaped from closed orbit. If we get an eccentricity greater than 1, we will have a hyperbola. If you want to study this topic in more detail, I advise you to first of all brush up on the geometry of conic sections in polar coordinates. After that, you should find the orbital equation in any good undergraduate classical mechanics textbook. Goldstein probably has it. Here is another point of interest. There is a theorem which dircetly links Kepler's law of areal velocity to the tangential terms of the general acceleration vector which you quoted. That gets rid of both the Euler force and the Coriolis force. Gravity orbits are a zero curl affair. To have Coriolis force, we need a curl. But let's get back to the original point. Thanks to SCZenz's comments to the anonymous, I now know that my mathematical reasoning does not need any citations. For a circular motion to occur, the second time differential of the radial distance must equal zero. Hence the sum of v^2/r and the inward centripetal force must equal zero. In the artificial circle, which is purely an artifact and doesn't involve any centrifugal pressure at all, your team have been arguing that the outward centrifugal force v^2/r is counterbalanced by an inward acting Coriolis force. This is nonsense on a number of counts. The Coriolis force never acts radially. The Coriolis force and the centrifugal force are always mutually perpendicular. Do you remember the acceleration expression which results if we act directly on v? It is vXω. That is the parent force of both Coriolis and centrifugal before it gets expanded into two mutually perpendicular components. Also,even if your team are correct and we can make the Coriolis force act radially inwards, then the result will be twice that of the centrifugal force. So the second order time differential of the radial distance will not be zero. Hence we can't have a circular motion. Those transformation equations are only designed to deal with actual rotation. To invoke the Coriolis force we need a physical curl such as we get in hydrodynamics when an element of a rotating fluid moves radially inwards (or outwards) within itself.David Tombe (talk) 04:55, 7 May 2008 (UTC)

I suggest you submit your physics reasoning to a physics journal, so that after it is published we can use it to explain to the readers of the wikipedia how David Tombe overturned basic physics.- (User) WolfKeeper (Talk) 05:01, 7 May 2008 (UTC)

Some remarks:

• The orbital equation in question is not a vector equation, it is just the EoM for the radial coordinate in polar coordinates. Any mumbling about terms being (not) radial is thus just gibberish since the terms have no direction.
• The v in the equation is somewhat misleading. It is not the speed of the orbiting object, it is r times phi dot; the tangential speed of the object. The equation is better understood in terms of l = r v the angular momentum per unit mass.
• The v term can be thought of an fictitious force induce by co-rotating coordinates. It encompasses components contributitions from the centrifugal, Euler and Coriolis forces.

(TimothyRias (talk) 09:09, 7 May 2008 (UTC))

Timothy, all that was just a quible. It bore no relationship to the point I was making to FyzixFighter. I'm fully aware of the fact that I used 'short cut' symbolism. I was merely trying to drive home the point that two opposing effects work in opposition to yield the second order time derivative of the radial distance.David Tombe (talk) 09:35, 7 May 2008 (UTC)

Where is the page on Colloquial Centrifugal Force ?

The current introduction ends with the sentence, Colloquially, the term "centrifugal force" is sometimes also used to refer to any force pushing away from a center; this article discusses only the centrifugal force related to rotating reference frames. So where is the page on colloquial centrifugal force? That's the page the readers want. This sentence is effectively the same as saying, If you are looking for centrifugal force, you have come to the wrong page.David Tombe (talk) 06:12, 7 May 2008 (UTC)

That would be an incredibly short article, since the above sentence says pretty much everything there is to say about that use of the term. Namely, that it refers to an outward pointing force. (TimothyRias (talk) 08:31, 7 May 2008 (UTC))

I could certainly trim a single article on centrifugal force down to a few key points. David Tombe (talk) 09:36, 7 May 2008 (UTC)

I think the current article could probably do with a section devoted to the colloquial use of the term. There are probably somethings that need to be explained with that respect. (TimothyRias (talk) 11:04, 7 May 2008 (UTC))

Probably everything to do with centrifugal force. David Tombe (talk) 11:32, 7 May 2008 (UTC)

It seems to me like the discussion of the colloquial "centrifugal force" in an inertial frame might belong on the page Centripetal force, which is already dealing with the situation of rotation in an inertial frame? Perhaps we could add a note to that sentence accordingly? (And make sure that the centripetal force article has a good enough discussion.) Also, regardless, that sentence should probably read: "any "force" pushing away from a center", with scare quotes around force, since it's not a force in the technical sense. Oops, let me rephrase for David: ...since reliable sources say that it's not a force in the technical sense. :-) --Steve (talk) 16:57, 7 May 2008 (UTC)

Please Produce The proof

I want to see the peer reviewed proof that justifies the statements made in the main article. These need to be peer reviewed journal articles or reccomendations from a physics education committee and cited in the main page. As far I can determine, there is no peer reviewed, critically examined proof of what is said in the main article. Citations which refer to sources that repeat or draw conclusions from other unproved sources are not acceptable. I want to see the actual real proof, not hearsay that it exists in theory.72.64.51.14 (talk) 16:03, 7 May 2008 (UTC)

Wikipedia has specific guidelines on what constitutes a reliable source. Most of the statements in the article are in essentially every intro university-level physics textbook, and every dedicated classical mechanics textbook, which are gold-standard reliable sources according to those guidelines. Are those good enough sources for you? If so, please point out any specific statements that you doubt, and it will be a straightforward task for me or you or anyone else to provide specific textbook references for them. If not, then your standards of proof are different than Wikipedia's, and this is not the right forum for you to be posting that request. This page only exists for the purpose of making this Wikipedia article a better article according to Wikipedia's own standards. :-P --Steve (talk) 16:34, 7 May 2008 (UTC)

Translation, you don't really know if what you state in the article is verified by a peer reviewed journal article or not, just as I suspected. Since it is clear that you don't have the proof as required by standard scientific procedure, it is a justifiable conclusion that this article is making nonscientific false statements. Again, please produce the proof from a peer reviewed journal article or physics education report that justifies the statements made in main article.72.64.51.14 (talk) 18:54, 7 May 2008 (UTC)

This is the wikipedia. If you have any reliable sources that show that can show that centrifugal force and coriolis force are defined or derived incorrectly, then by all means give it here. If you can't understand the standard proofs, then that's not our problem in any way, shape or form.- (User) WolfKeeper (Talk) 19:03, 7 May 2008 (UTC)

Textbooks are a perfectly fine source. Peer review journals except references to textbooks, so why shouldn't wikipedia? If anything, textbooks usually provide much more extensive proofs of statements, whereas journal articles usually state "after some simple algebra..." (TimothyRias (talk) 20:41, 7 May 2008 (UTC))

Thank you. As I understand it, you are officially stating that Wikipedia does not have a peer reviewed journal paper or physics education committe report to validate what you state in the main article. Therefore, I demand that you accept Mr Tombe's edits as valid edits, since you have failed to prove him to be wrong. He has produced textbook citations which back up his position, while you have produced nothing to validate your opinions. Evidently Wikipedia policy has failed in this case to produce the required proof to support the claims made in the main article. I insist that you correct the mistakes in this article, and allow Mr Tombe to make edits to this article. You have totally failed to prove him to be wrong and your actions and behavior are certainly objectionable in this matter, as you have behaved unfairly and rudely to him. You also need to correct these and apologise to him officially.72.64.51.14 (talk) 21:40, 7 May 2008 (UTC)

As far as I see, Mr Tombe has not produced any textbook citations to back up any part of his position. Other editors have. Take for example "Analytical Mechanics", Hand & Finch pg 267 (1998); Oxford's "A Dictionary of Physics" (1996); "McGraw-Hill Dictionary of Physics" (1984) to name a few that support the current consensus version of the article. --FyzixFighter (talk) 23:00, 7 May 2008 (UTC)

FyzixFighter, I refered you to Goldstein's Classical Mechanics. There, as well as in many other applied maths textbooks, you will see the orbital equation which I described to you above. That equations makes it clear that the second time derivative of radial distance is only zero when we have two opposing forces cancelling each other out, one of which takes the form v^2/r outwards.

Anome never demands citations from other peoples' edits. He only demands citations for my edits. And when I give citations, he ignores them and continues to demand citations.

When I give maths reasoning, I get the red card held up against me. When Timothy Rias gives maths reasoning, SCZenz comes in to say that it's all fine. David Tombe (talk) 06:29, 8 May 2008 (UTC)

Thank you gentlemen. You have again failed to meet the minimum requirement of proof in science. That is a peer reviewed journal article that has been reviewed, discussed, debated, and validated. You have no physics education committe report that produces reccomendations, resulting from physics education studies, and justified by a peer reviewed journal paper that scientifically validates that what you write in the main article is correct. You are basically citing only opinion, and that opinion is not validated by any scientific procedure that I can determine. Therefore your main article claims are false and invalid and Mr Tombe has very right to dispute them and insist that they be changed. Your refusal to permit this is an injustice to him. Wikipipedia needs to correct this officially. I far as I can see Wikipedia policy has been officially used to abuse and insult Mr Tombe and that injustice needs to be corrected. Your failure to produce the required proof is a disgrace.72.84.68.195 (talk) 13:38, 8 May 2008 (UTC)

I can't get my hands on Goldstein's at the moment. But in the mean time while I'm getting my hands on a copy, here's something from "Intermediate Classical Mechanics" Joseph Norwood Jr, pg 196 (1979 published by Prentice Hall):

"Suppose, as an example, that a body rotates about the sun. The only real force is the force (gravitational in the case of the earth and the sun) toward the center. An observer on the rotating body notes that the body does not fall toward the center. In order to reconcile this observation with the requirement that the net radial force vanish-that is, that the circular orbit be maintained-the observer postulates an additional force, the centrifugal force. This is an artificial construct that arises solely from our wish to extend Newton's second law to a noninertial system. The same comments apply to the Coriolis force; this force is necessary to describe motion relative to the rotating body."

I'm pretty sure that this satisfies WP:RS. --FyzixFighter (talk) 15:27, 8 May 2008 (UTC)

Citation for Taylor? That quote looks good to me. A lot of this book is on line at Taylor. I think it is worth referencing - do you have a page number? Brews ohare (talk) 16:30, 8 May 2008 (UTC)

FyzixFighter, I don't think that Goldstein will overtly recognize centrifugal force either. It will adopt the same attitude as your book and work on the premises that gravity is the only force involved. But when the chips are down and the orbital equation appears, there will be two terms acting in opposition to each other in the radial direction. There will be a gravity term acting radially inwards and a term of the basic mathematical form v^2/r acting radially outwards. Whatever that v^2/r is, it is certainly not an artificial construct and it certainly doesn't arise because of any human desires as your book seems to suggest. It works in tandem (opposition) with gravity to produce conic section orbits.

A high quality textbook will generally remain silent on the issue of what this term actually is. It will be quietly borrowed from that general acceleration equation that we have been looking at. And as you must surely be aware, that general acceleration equation merely exposes inertia in the Cartesian frame to be the centrifugal force and the Coriolis force in a polar frame.

Yes, you are correct in that no modern textbook is likely to overtly declare the centrifugal term to be real. In fact, your book's declaration that it is artificial should surely alarm you. To claim such with regards to that scenario is the height of delusion.

Now I'd like to draw your attention to this line in your reference,

In order to reconcile this observation with the requirement that the net radial force vanish-that is, that the circular orbit be maintained

Now consider the artificial circular motion which is associated with viewing a stationary object from a rotating frame. How does it reconcile with this requirement? According to the 'Fictitious party' there is a radially outward centrifugal force and a radially inward Coriolis force that is twice as large. Yet if we are to have a circular orbit the centripetal force and the centrifugal force must be balanced.

The reality is that the equations for the coordinate frame transformation are only designed to cater for co-rotating objects. This condition is totally satisfied in meteorology.

Can you show me an explicit citation stating that these equations apply to objects that are stationary in the inertial frame. I wouldn't be entirely surprised if you could. But nevertheless, I would like to see it explicitly stated in a book. I have a feeling that the restriction to co-rotation has been overlooked by many people who have been introduced to these equations, and the error has been passed on from textbook writer to textbook writer.

Or perhaps the error isn't even in the textbooks and the mistake lies entirely with the readers. That's why I'd like you to find an explicit reference which overtly states that these equations apply to objects that are at rest in the inertial frame. David Tombe 119.42.65.152 (talk) 16:11, 8 May 2008 (UTC)

The Swerving car

Nobody ever mentions frames of reference when they describe the effects that take place due to centrifugal force inside a swerving car. They talk about these events as they stand in their kitchen, which is an inertial frame, and they state that as the car swerved around the corner, they got flung to the side door.

It is a matter of opinion which I don't subcribe to, to state that these events are more conveniently described from a rotating frame of reference. No such frame is needed in the description. When have you ever heard anybody going to the bother of explaining that as they viewed things from within the car, they were accelerated twoards the side door. The man standing watching it from the street saw exactly the same thing.

lol. But the man watching from the street saw no flung. All they saw was linear momentum. And describing what happened in the car is describing it from the frame of reference of the car- which is an accelerating frame.- (User) WolfKeeper (Talk) 17:10, 7 May 2008 (UTC)

Such an argument however does not necessarily extent to the Coriolis force in relation to meteorology. 119.42.69.123 (talk) 16:16, 7 May 2008 (UTC)

lol- (User) WolfKeeper (Talk) 17:10, 7 May 2008 (UTC)

Wolfkeeper, the man in the street is quite capable of observing a radial acceleration towards the side door. We don't need to consider a rotating frame of reference to observe this.David Tombe (talk) 06:23, 8 May 2008 (UTC)

But the man isn't corotating. Why does he move towards the side door?- (User) WolfKeeper (Talk) 07:10, 8 May 2008 (UTC)

Wolfkeeper, the man in the street sees the man inside the car getting flung to the side door. David Tombe (talk) 09:55, 8 May 2008 (UTC)

I repeat, the man in the car isn't corotating with the car, since he's on a skiddy seat, why does he get flung to the side door inside the car? According to you, centrifugal force only happens in corotation. If he's not rotating (the man on the street says he's going in a straight line!), then there's no centrifugal force is there?- (User) WolfKeeper (Talk) 10:09, 8 May 2008 (UTC)

Wolfkeeper, the man in the car is co-rotating. The back of his seat pushes him tangentially. This induces a vXω force radially. If he wasn't co-rotating with the car, he wouldn't be in the car, and he wouldn't be experiencing any outward tangential force.

And yes, this radially outward acceleration translates into straight line motion in the Cartesian frame. Centrifugal force in the polar frame is the same thing as inertia in the Cartesian frame.

Look at the conversion equation. Then remove the tangential components because of Kepler's law of areal velocity. Centrifugal force stands out as an inbuilt feature of straight line motion. David Tombe 119.42.65.152 (talk) 16:32, 8 May 2008 (UTC)

The way forward

Hi everyone. I understand that there are already textbook references that support the current version of the article straight down the line. However, it would be helpful if users would add in-line citations to sections that are being "warred" over. Talk page discussion is not settling this "argument"; I think administrative action will, but the case for administrative action is far stronger if directly-cited statements are being removed. I am willing to use my knowledge of physics to evaluate whether a source actually supports a statement, but not to treat a statement as cited just because I personally know it's correct and that it could be. So if instead of just reverting, you would consider in-line citations for the statements you re-add, it would save us all time in the end! -- SCZenz (talk) 07:30, 8 May 2008 (UTC)

What about the Goldstein classical mechanics textbook reference that states the orbital equation and shows that the second order time derivative of radial distance arises from an inward acting gravity term and an outward acting centrifugal term? Why is that not allowed as evidence that centrifugal force is real?

What about the Bernoulli and Maxwell references that show that they believed centrifugal force to be real?

And why should we need any references at all to state that centrifugal force is connected with rotation?David Tombe (talk) 10:13, 8 May 2008 (UTC)

I notice that Timothy Rias has responded to this message by filling up the introduction with references for matters which are not in dispute. That is a bad sign. It shows that he has lost sight of the higher picture. David Tombe (talk) 10:32, 8 May 2008 (UTC)

In reply to the above statement. I can provide just as many textbook references that contradict what is stated in the main article. Therefore I must conclude, that since I have just as many references that contradict what you say, then what you say is not justified by your selection of certain references that agree with what you beleive. That is not science. So you need to prove what you say is true, and you have not done it.72.84.68.195 (talk) 14:25, 8 May 2008 (UTC)

If you can provide such textbook references, please do so. -- SCZenz (talk) 22:29, 8 May 2008 (UTC)

Reply to Wolfkeeper on Curl and Coriolis

Wolfkeeper, I am fully aware of the fact that the Coriolis force doesn't involve any change in kinetic energy. But the Coriolis force does not occur in a zero curl field. There is no vorticity in the gravitational field that could invoke the Coriolis force. Kepler's law of areal velocity eliminates the Coriolis force from gravitational problems.

Curl is a measure of the sum of forces around a circle in a field of force. If a force sums to zero- then it creates no change in energy, and conversely if it sums to non zero, then it is non conservative. Coriolis creates no change in energy and hence has no curl.- (User) WolfKeeper (Talk) 20:13, 8 May 2008 (UTC)

There is however Coriolis force in hydrodynamics because there can be vorticity. The ω is to all intents and purposes the vorticity.David Tombe (talk) 10:24, 8 May 2008 (UTC)

Oh sure, vortexes have curl. Stick a windmill in a vortex, and you can generate energy, no problemo. But the coriolis force due to that vortex motion does not.- (User) WolfKeeper (Talk) 20:13, 8 May 2008 (UTC)

David Tombe blocked for 31 hours

I have just blocked David for 31 hours for reinsertion of the same unreferenced assertions as before (see this diff), in spite of extensive warnings regarding the need to adhere to Wikipedia's polices. David, you are welcome to edit again when the block expires, but please try to edit according the WP:V and WP:NOR policies; that is to say, please provide verifiable cites to third-party reliable sources that back up your assertions. -- The Anome (talk) 11:00, 8 May 2008 (UTC)

Sir, Again you have created an injustice with respect to Mr Tombe. As stated above, what you state in the main article is false, and Mr Tombe has every right to dispute it. Your policy is a disgrace as I stated above. You need to correct your behavior in this matter. Mr Tombe has clearly stated his sources on this talk page and you have none to prove him wrong. You need to produce the proof and you have not produced it.72.84.68.195 (talk) 13:54, 8 May 2008 (UTC)

The burden of proof lies with the person making the claim, and the consensus point of view, by contrast, meets this requirement by already providing multiple supporting cites to reliable sources. Since I cannot find the sources you are referring to above on his talk page, other than the Maxwell and Bernoulli quotes already excluded by the WP:SYN policy, I would appreciate it if you could tell me what they are. Something like a physics textbook or peer-reviewed paper saying "centrifugal force is a real, not fictitious, force" would meet the requirements just fine. The mere use of the concept of centrifugal force will not, since, as the mainstream opinion expressed in the consensus version of the article states, using the concept of a fictitious centrifugal d'Alembert force is a perfectly legitimate verbal and computational shorthand for describing many simple rotating physical systems, without any implication that it should be confused with an actual physical force (which, for example, would conserve momentum, unlike the fictitious centrifugal force). -- The Anome (talk) 18:08, 8 May 2008 (UTC)

Thank you for your answer. I take your answer to mean that you are making excuses for the fact that you do not have the demanded proof and that you feel entirely justified in treating Mr Tombe unfairly as a deliberate policy of Wikipedia. You have answered my demand by making a counter demand, and that is not a valid procedure in a debate. I ignore your demand, since I make no assertions other than that you produce the required proof and apologise to Mr Tombe, since he is certainly justified in disputing what is stated in Wikipedia, when you have not produced a satisfactory proof that what you say is valid physics.

The issue now at hand is a simple matter of your proving your case not me proving my case. I am simply demanding that you prove your case in order to justify that what you say in the subject article on centrifugal force is true. This is what Mr Tombe disputes and your editors response demonstrates that they did not do the investigation required to back up what they state has actually been proved. This could have been easily accomplished if you had editors who were competent to do it, and not prone to nasty, offensive and rude, disputation. It is now certainly clear that there is no proof of what your editors claim is true, and that you should not be supporting them, but instead demand that they produce the proof, or stop disputing what Mr Tombe says in a nasty manner. You respond to my simple request for proof in the same manner as you did with Mr Tombe, rudely. The issue is the question of the justification of certain revisionist statements of physics, and the request is simply that you produce peer reviewed journal papers, and physics education committee reports that prove what you say is actually true and not a mistake in the opinion of certain writers from which your editors have uncritically copied statements in physics. I look forward to your providing these required proofs and an official apology from you to Mr Tombe. 72.64.50.119 (talk) 22:21, 8 May 2008 (UTC)

The article cites five independent sources for the consensus content:

1. Wolfram Scienceworld website.
2. Britannica online encyclopedia.
3. Stephen T. Thornton & Jerry B. Marion (2004). Classical Dynamics of Particles and Systems, 5th Edition, Belmont CA: Brook/Cole, Chapter 10. ISBN 0534408966.
4. John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books, pp. 343-344. ISBN 189138922X.
5. Vladimir Igorevich Arnolʹd (1989). Mathematical Methods of Classical Mechanics. Berlin: Springer, §27 pp. 129 ff.. ISBN 0387968903.

URLs and page references are provided in the article itself.

• Wolfram Scienceworld is a well-regarded resource edited by Eric W. Weisstein, who is a PhD-educated planetary astronomer and physicist. It is published by Wolfram Research, famous for their Mathematica software, and for their founder Stephen Wolfram.

• The Encyclopædia Britannica is the world's highest-regarded English-language general encyclopedia.

• John Robert Taylor is Professor of Physics at the University of Colorado in Boulder. You can see the book's back cover for his other credentials. His book is available online, so you can read the cited sections directly.

• Vladimir Igorevich Arnolʹd is a famous and highly esteemed mathematician. He works at the Steklov Mathematical Institute in Moscow and at the University of Paris IX. As of 2006 he was reported to have the highest citation index among Russian scientists, and an h-index of 40. His list of mathematical awards and other honours is too lengthy to list here. He solved Hilbert's 13th problem at the age of 19. See this biography for more details.

I'm sure the credentials of Stephen T. Thornton & Jerry B. Marion can be tracked down with similar ease, but I don't have the time to do so right now.

In each case, each work has a publisher that is independent of its author. The combination of all of these sources more than suffices to comply with the Wikipedia:Verifiability policy, as well as WP:NOR and WP:NPOV, which is all that is required here.

-- The Anome (talk) 22:58, 8 May 2008 (UTC) [updated with more details 23:45, 8 May 2008 (UTC)]

Your answer is not responsive to the demand. I repeat produce the proof as required, and apologise to Mr Tombe for the nasty behavior of your editors.72.64.50.119 (talk) 23:04, 8 May 2008 (UTC)

Please read Wikipedia's WP:NPOV, WP:V and WP:OR policies, which are the relevant principles to be applied here. If you would like to start a new encyclopedia which conforms to your ideas of how an encyclopedia should be run, you are welcome to do so. -- The Anome (talk) 23:08, 8 May 2008 (UTC)

Relevant textbook discusion for debate with Tombe

Perhaps the discussion at Taylor, p. 358, which seems to cover many of the points raised, and can be viewed at Google books, would help to settle the disputes. Brews ohare (talk) 19:56, 8 May 2008 (UTC)

That seems to be a good general reference for many articles, including this one, fictitious force, and Coriolis force. Of course, many textbooks would, but the fact that it is available online makes it very accessible to readers. Whether this will settle any disputes remains to be seen. But one way or the other this place is going to calm down eventually. Until then, I will for my part avoid discussing physics, and only discuss whether particular edits are supported by reliable sources or not. In the end, that is what really matters here on Wikipedia. --PeR (talk) 20:38, 8 May 2008 (UTC)

Linguistics and merger with reactive centrifugal force

There are clearly at least three interpretations of the term "Centrifugal force"

1. A pseudo force
2. A reaction force as described in reactive centrifugal force
3. Any (real) force that is directed away from the center of rotation

I think most people here will agree that the most common interpretation of the term "Centrifugal force" is the pseudo force. The question is, how important are the other two interpretations? I'm beginning to think that maybe giving the second one its own article is undue weight when in fact it is just a small minority that uses it in that precise sense. Note that the second interpretation is a subset of the third, so in most cases you can't tell from a quote that it only implies the second meaning and not the third. There are some cases where it would clearly be strange to use the term as in the second interpretation. For example, consider a binary star. For star A, the gravity from star B provides a centripetal force. Consequently, the gravitational pull on star B from star A would be the "reactive centrifugal force" even though it is not acting away from the center of rotation.

My conclusion is that both interpretations 2 and 3 are significant enough to warrant inclusion in this article, perhaps in an "etymology" section, but neither is important enough to have its own article. --PeR (talk) 21:00, 8 May 2008 (UTC)

I'd agree. The main advantage of separate articles just now is to avoid the imbroglio. Brews ohare (talk) 22:11, 8 May 2008 (UTC)

Under the rules of an encyclopedia an encyclopedia is supposed to have a topic, and describe it well; and it's not supposed to be a 'different meanings of a phrase'. The only major connection I can really see between them is the same name; and that's specifically excluded under wp:NOT- (User) WolfKeeper (Talk) 23:38, 8 May 2008 (UTC)

Lots of wikipedia articles have etymology sections, and some of those include archaic meanings of the term. (See, for example, stereotype.) So the question is really whether reactive centrifugal force is an important concept today (in which case it should have its own article) or just an archaic term (in which case a mention in an etymology section will suffice). --PeR (talk) 07:02, 9 May 2008 (UTC)

A couple more references

I've just been scouting around for some more citable references.

Here's a peer-reviewed paper that describes centrifugal force as fictitious, for those that insist that only peer-reviewed sources are valid: Merab Gogberashvili, Coriolis Force and Sagnac Effect, Found.Phys.Lett. 15 (2002) 487-493. Quote: "In the rotating frame two fictitious gravity-like forces appear, namely the centrifugal and Coriolis forces. This is an illustration of the equivalence principle, which asserts that gravity and the accelerated motion are locally indistinguishable."

And for those who like citation by independent third-party reviews of the field, and/or appeals to authority: Richard Feynman, quoted in The Natural Philosophy of Leibniz by Kathleen Okruhlik, James Robert Brown (Springer, 1985, ISBN 9027721459, page 138) as saying (referring to rotation and centrifugal force) "These forces are due merely to the fact that the observer does not have Newton's coordinate system, which is the simplest coordinate system." -- The Anome (talk) 00:40, 9 May 2008 (UTC)

Anome misrepresents what the edit war is about

Anome has totally misrepresented what the edit war is about. He has presented this war as being over the issue of whether or not centrifugal force is real.

The war is not about whether or not centrifugal force is real, although that did become a side issue when Anome opened up a special section entitled 'Is the centrifugal force real?'.

The war is not about whether the term fictitious force is applied to centrifugal force in the textbooks. We all know that it is.

The war is about the fact that all attempts to mention the cause of centrifugal get instantly erased from the article. That cause is rotation. And we don't need any citations to back up that assertion because it is a well known and undisputed fact. 58.147.58.54 (talk) 06:19, 9 May 2008 (UTC)

David, you are not allowed to evade a block by not logging in. When you do that, an admin may reset your block, and the IP that you are editing from may also be blocked. --PeR (talk) 07:08, 9 May 2008 (UTC)

58.147.58.54 is not David Tombe, I don't think. 119.42.65.152 is and has been blocked. The way, the truth, and the light (talk) 07:43, 9 May 2008 (UTC)

According to whois, both of those IP-addresses are from the same area. My guess is that one is dialup and the other is from an internet café. But of course there is a nonzero probability that there are two different people who live in the same area, share the same views on this subject, and have very similar editing style. --PeR (talk) 07:58, 9 May 2008 (UTC)

(I think that discussing with David Tombe and its (virtual?) defenders is a complete loss of time. Not only he obviously does not have a clue about this topic, but is completely unwilling to try understanding what people tell him. Anyway...) There is no cause for the centrifugal force! It just appears (together with other virtual forces) when you compute the acceleration of a body as seen from a non-inertial frame of reference, and want to interpret this acceleration according to Newton's law (i.e., as being due to forces acting on the body). Then obviously, you get, additionnaly to the real forces possibly acting on the body, additional terms (corresponding to virtual forces) which are merely due to the fact that the observer is in a non-inertial frame of reference (for example rotating). And of course it does also apply to objects that are at rest w.r.t. some inertial frame of reference (and would be seen as moving from the non-inertial one as if subjected to some forces (that do not really exist, that's why they are called virtual forces)). That's a completely obvious mathematical fact, and certainly not the source of any debate among people with any real understanding of physics...--129.194.8.73 (talk) 08:17, 9 May 2008 (UTC)

129.194.8.73, Does a centrifuge work if it is not rotating?119.42.68.141 (talk) 10:05, 9 May 2008 (UTC)