Climate model

Numerical climate models (or climate system models) are mathematical models that can simulate the interactions of important drivers of climate. These drivers are the atmosphere, oceans, land surface and ice. Scientists use climate models to study the dynamics of the climate system and to make projections of future climate and of climate change. Climate models can also be qualitative (i.e. not numerical) models and contain narratives, largely descriptive, of possible futures.[1]
Climate models take account of incoming energy from the Sun as well as outgoing energy from Earth. An imbalance results in a change in temperature. The incoming energy from the Sun is in the form of short wave electromagnetic radiation, chiefly visible and short-wave (near) infrared. The outgoing energy is in the form of long wave (far) infrared electromagnetic energy. These processes are part of the greenhouse effect.
Climate models vary in complexity. For example, a simple radiant heat transfer model treats the Earth as a single point and averages outgoing energy. This can be expanded vertically (radiative-convective models) and horizontally. More complex models are the coupled atmosphere–ocean–sea ice global climate models. These types of models solve the full equations for mass transfer, energy transfer and radiant exchange. In addition, other types of models can be interlinked. For example Earth System Models include also land use as well as land use changes. This allows researchers to predict the interactions between climate and ecosystems.
Climate models are systems of differential equations based on the basic laws of physics, fluid motion, and chemistry. Scientists divide the planet into a 3-dimensional grid and apply the basic equations to those grids. Atmospheric models calculate winds, heat transfer, radiation, relative humidity, and surface hydrology within each grid and evaluate interactions with neighboring points. These are coupled with oceanic models to simulate climate variability and change that occurs on different timescales due to shifting ocean currents and the much larger combined volume and heat capacity of the global ocean. External drivers of change may also be applied. Including an ice-sheet model better accounts for long term effects such as sea level rise.
Uses
[edit]There are three major types of institution where climate models are developed, implemented and used:
- National meteorological services: Most national weather services have a climatology section.
- Universities: Relevant departments include atmospheric sciences, meteorology, climatology, and geography.
- National and international research laboratories: Examples include the National Center for Atmospheric Research (NCAR, in Boulder, Colorado, US), the Geophysical Fluid Dynamics Laboratory (GFDL, in Princeton, New Jersey, US), Los Alamos National Laboratory, the Hadley Centre for Climate Prediction and Research (in Exeter, UK), the Max Planck Institute for Meteorology in Hamburg, Germany, or the Laboratoire des Sciences du Climat et de l'Environnement (LSCE), France.
Big climate models are essential but they are not perfect. Attention still needs to be given to the real world (what is happening and why). The global models are essential to assimilate all the observations, especially from space (satellites) and produce comprehensive analyses of what is happening, and then they can be used to make predictions/projections. Simple models have a role to play that is widely abused and fails to recognize the simplifications such as not including a water cycle.[2]
General circulation models (GCMs)
[edit]
A general circulation model (GCM) is a type of climate model. It employs a mathematical model of the general circulation of a planetary atmosphere or ocean. It uses the Navier–Stokes equations on a rotating sphere with thermodynamic terms for various energy sources (radiation, latent heat). These equations are the basis for computer programs used to simulate the Earth's atmosphere or oceans. Atmospheric and oceanic GCMs (AGCM and OGCM) are key components along with sea ice and land-surface components.
GCMs and global climate models are used for weather forecasting, understanding the climate, and forecasting climate change.
Atmospheric GCMs (AGCMs) model the atmosphere and impose sea surface temperatures as boundary conditions. Coupled atmosphere-ocean GCMs (AOGCMs, e.g. HadCM3, EdGCM, GFDL CM2.X, ARPEGE-Climat)[4] combine the two models. The first general circulation climate model that combined both oceanic and atmospheric processes was developed in the late 1960s at the NOAA Geophysical Fluid Dynamics Laboratory[5] AOGCMs represent the pinnacle of complexity in climate models and internalise as many processes as possible. However, they are still under development and uncertainties remain. They may be coupled to models of other processes, such as the carbon cycle, so as to better model feedback effects. Such integrated multi-system models are sometimes referred to as either "earth system models" or "global climate models."
Versions designed for decade to century time scale climate applications were originally created by Syukuro Manabe and Kirk Bryan at the Geophysical Fluid Dynamics Laboratory (GFDL) in Princeton, New Jersey.[3] These models are based on the integration of a variety of fluid dynamical, chemical and sometimes biological equations.Energy balance models (EBMs)
[edit]Simulation of the climate system in full 3-D space and time was impractical prior to the establishment of large computational facilities starting in the 1960s. In order to begin to understand which factors may have changed Earth's paleoclimate states, the constituent and dimensional complexities of the system needed to be reduced. A simple quantitative model that balanced incoming/outgoing energy was first developed for the atmosphere in the late 19th century.[6] Other EBMs similarly seek an economical description of surface temperatures by applying the conservation of energy constraint to individual columns of the Earth-atmosphere system.[7]
Essential features of EBMs include their relative conceptual simplicity and their ability to sometimes produce analytical solutions.[8]: 19 Some models account for effects of ocean, land, or ice features on the surface budget. Others include interactions with parts of the water cycle or carbon cycle. A variety of these and other reduced system models can be useful for specialized tasks that supplement GCMs, particularly to bridge gaps between simulation and understanding.[9][10]
Zero-dimensional models
[edit]Zero-dimensional models consider Earth as a point in space, analogous to the pale blue dot viewed by Voyager 1 or an astronomer's view of very distant objects. This dimensionless view while highly limited is still useful in that the laws of physics are applicable in a bulk fashion to unknown objects, or in an appropriate lumped manner if some major properties of the object are known. For example, astronomers know that most planets in our own solar system feature some kind of solid/liquid surface surrounded by a gaseous atmosphere.
Model with combined surface and atmosphere
[edit]A very simple model of the radiative equilibrium of the Earth is
where
- the left hand side represents the total incoming shortwave power (in Watts) from the Sun
- the right hand side represents the total outgoing longwave power (in Watts) from Earth, calculated from the Stefan–Boltzmann law.
The constant parameters include
- S is the solar constant – the incoming solar radiation per unit area—about 1367 W·m−2
- r is Earth's radius—approximately 6.371×106 m
- π is the mathematical constant (3.141...)
- is the Stefan–Boltzmann constant—approximately 5.67×10−8 J·K−4·m−2·s−1
The constant can be factored out, giving a nildimensional equation for the equilibrium
where
- the left hand side represents the incoming shortwave energy flux from the Sun in W·m−2
- the right hand side represents the outgoing longwave energy flux from Earth in W·m−2.
The remaining variable parameters which are specific to the planet include
- is Earth's average albedo, measured to be 0.3.[11][12]
- is Earth's average surface temperature, measured as about 288 K as of year 2020[13]
- is the effective emissivity of Earth's combined surface and atmosphere (including clouds). It is a quantity between 0 and 1 that is calculated from the equilibrium to be about 0.61. For the zero-dimensional treatment it is equivalent to an average value over all viewing angles.
This very simple model is quite instructive. For example, it shows the temperature sensitivity to changes in the solar constant, Earth albedo, or effective Earth emissivity. The effective emissivity also gauges the strength of the atmospheric greenhouse effect, since it is the ratio of the thermal emissions escaping to space versus those emanating from the surface.[14]
The calculated emissivity can be compared to available data. Terrestrial surface emissivities are all in the range of 0.96 to 0.99[15][16] (except for some small desert areas which may be as low as 0.7). Clouds, however, which cover about half of the planet's surface, have an average emissivity of about 0.5[17] (which must be reduced by the fourth power of the ratio of cloud absolute temperature to average surface absolute temperature) and an average cloud temperature of about 258 K (−15 °C; 5 °F).[18] Taking all this properly into account results in an effective earth emissivity of about 0.64 (earth average temperature 285 K (12 °C; 53 °F)).[citation needed]
Models with separated surface and atmospheric layers
[edit]
Dimensionless models have also been constructed with functionally separated atmospheric layers from the surface. The simplest of these is the zero-dimensional, one-layer model,[19] which may be readily extended to an arbitrary number of atmospheric layers. The surface and atmospheric layer(s) are each characterized by a corresponding temperature and emissivity value, but no thickness. Applying radiative equilibrium (i.e conservation of energy) at the interfaces between layers produces a set of coupled equations which are solvable.[20]
Layered models produce temperatures that better estimate those observed for Earth's surface and atmospheric levels.[21] They likewise further illustrate the radiative heat transfer processes which underlie the greenhouse effect. Quantification of this phenomenon using a version of the one-layer model was first published by Svante Arrhenius in year 1896.[6]
Radiative-convective models
[edit]Water vapor is a main determinant of the emissivity of Earth's atmosphere. It both influences the flows of radiation and is influenced by convective flows of heat in a manner that is consistent with its equilibrium concentration and temperature as a function of elevation (i.e. relative humidity distribution). This has been shown by refining the zero dimension model in the vertical to a one-dimensional radiative-convective model which considers two processes of energy transport:[22]
- upwelling and downwelling radiative transfer through atmospheric layers that both absorb and emit infrared radiation
- upward transport of heat by air and vapor convection, which is especially important in the lower troposphere.
Radiative-convective models have advantages over simpler models and also lay a foundation for more complex models.[23] They can estimate both surface temperature and the temperature variation with elevation in a more realistic manner. They also simulate the observed decline in upper atmospheric temperature and rise in surface temperature when trace amounts of other non-condensible greenhouse gases such as carbon dioxide are included.[22]
Other parameters are sometimes included to simulate localized effects in other dimensions and to address the factors that move energy about Earth. For example, the effect of ice-albedo feedback on global climate sensitivity has been investigated using a one-dimensional radiative-convective climate model.[24][25]
Higher-dimension models
[edit]The zero-dimensional model may be expanded to consider the energy transported horizontally in the atmosphere. This kind of model may well be zonally averaged. This model has the advantage of allowing a rational dependence of local albedo and emissivity on temperature – the poles can be allowed to be icy and the equator warm – but the lack of true dynamics means that horizontal transports have to be specified.[26]
Early examples include research of Mikhail Budyko and William D. Sellers who worked on the Budyko-Sellers model).[27][28] This work also showed the role of positive feedback in the climate system and has been considered foundational for the energy balance models since its publication in 1969.[7][29]
Earth systems models of intermediate complexity (EMICs)
[edit]Depending on the nature of questions asked and the pertinent time scales, there are, on the one extreme, conceptual, more inductive models, and, on the other extreme, general circulation models operating at the highest spatial and temporal resolution currently feasible. Models of intermediate complexity bridge the gap. One example is the Climber-3 model. Its atmosphere is a 2.5-dimensional statistical-dynamical model with 7.5° × 22.5° resolution and time step of half a day; the ocean is MOM-3 (Modular Ocean Model) with a 3.75° × 3.75° grid and 24 vertical levels.[30]
Box models
[edit]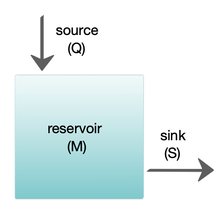
Box models are simplified versions of complex systems, reducing them to boxes (or reservoirs) linked by fluxes. The boxes are assumed to be mixed homogeneously. Within a given box, the concentration of any chemical species is therefore uniform. However, the abundance of a species within a given box may vary as a function of time due to the input to (or loss from) the box or due to the production, consumption or decay of this species within the box.[citation needed]
Simple box models, i.e. box model with a small number of boxes whose properties (e.g. their volume) do not change with time, are often useful to derive analytical formulas describing the dynamics and steady-state abundance of a species. More complex box models are usually solved using numerical techniques.[citation needed]
Box models are used extensively to model environmental systems or ecosystems and in studies of ocean circulation and the carbon cycle.[31] They are instances of a multi-compartment model.
History
[edit]In 1956, Norman Phillips developed a mathematical model that realistically depicted monthly and seasonal patterns in the troposphere. This was the first successful climate model.[32][33] Several groups then began working to create general circulation models.[34] The first general circulation climate model combined oceanic and atmospheric processes and was developed in the late 1960s at the Geophysical Fluid Dynamics Laboratory, a component of the U.S. National Oceanic and Atmospheric Administration.[35]
By 1975, Manabe and Wetherald had developed a three-dimensional global climate model that gave a roughly accurate representation of the current climate. Doubling CO2 in the model's atmosphere gave a roughly 2 °C rise in global temperature.[36] Several other kinds of computer models gave similar results: it was impossible to make a model that gave something resembling the actual climate and not have the temperature rise when the CO2 concentration was increased.
By the early 1980s, the U.S. National Center for Atmospheric Research had developed the Community Atmosphere Model (CAM), which can be run by itself or as the atmospheric component of the Community Climate System Model. The latest update (version 3.1) of the standalone CAM was issued on 1 February 2006.[37][38][39] In 1986, efforts began to initialize and model soil and vegetation types, resulting in more realistic forecasts.[40] Coupled ocean-atmosphere climate models, such as the Hadley Centre for Climate Prediction and Research's HadCM3 model, are being used as inputs for climate change studies.[34]Increase of forecasts confidence over time
[edit]The IPCC stated in 2010 it has increased confidence in forecasts coming from climate models:
"There is considerable confidence that climate models provide credible quantitative estimates of future climate change, particularly at continental scales and above. This confidence comes from the foundation of the models in accepted physical principles and from their ability to reproduce observed features of current climate and past climate changes. Confidence in model estimates is higher for some climate variables (e.g., temperature) than for others (e.g., precipitation). Over several decades of development, models have consistently provided a robust and unambiguous picture of significant climate warming in response to increasing greenhouse gases."[41]
Coordination of research
[edit]The World Climate Research Programme (WCRP), hosted by the World Meteorological Organization (WMO), coordinates research activities on climate modelling worldwide.
A 2012 U.S. National Research Council report discussed how the large and diverse U.S. climate modeling enterprise could evolve to become more unified.[42] Efficiencies could be gained by developing a common software infrastructure shared by all U.S. climate researchers, and holding an annual climate modeling forum, the report found.[43]
Issues
[edit]Electricity consumption
[edit]Cloud-resolving climate models are nowadays run on high intensity super-computers which have a high power consumption and thus cause CO2 emissions.[44] They require exascale computing (billion billion – i.e., a quintillion – calculations per second). For example, the Frontier exascale supercomputer consumes 29 MW.[45] It can simulate a year’s worth of climate at cloud resolving scales in a day.[46]
Techniques that could lead to energy savings, include for example: "reducing floating point precision computation; developing machine learning algorithms to avoid unnecessary computations; and creating a new generation of scalable numerical algorithms that would enable higher throughput in terms of simulated years per wall clock day."[44]
Parametrization
[edit]See also
[edit]- Atmospheric reanalysis
- Chemical transport model
- Atmospheric Radiation Measurement (ARM) (in the US)
- Climate Data Exchange
- Climateprediction.net
- Numerical Weather Prediction
- Static atmospheric model
- Tropical cyclone prediction model
- Verification and validation of computer simulation models
- CICE sea ice model
References
[edit]- ^ IPCC (2014). "AR5 Synthesis Report - Climate Change 2014. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change" (PDF): 58.
Box 2.3. 'Models' are typically numerical simulations of real-world systems, calibrated and validated using observations from experiments or analogies, and then run using input data representing future climate. Models can also include largely descriptive narratives of possible futures, such as those used in scenario construction. Quantitative and descriptive models are often used together.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Trenberth, Kevin E. (2022). "Chapter 1: Earth and Climate System". The Changing Flow of Energy Through the Climate System (1 ed.). Cambridge University Press. doi:10.1017/9781108979030. ISBN 978-1-108-97903-0.
- ^ a b "The First Climate Model". NOAA 200th Celebration. 2007.
- ^ [1] Archived 27 September 2007 at the Wayback Machine
- ^ "NOAA 200th Top Tens: Breakthroughs: The First Climate Model". noaa.gov.
- ^ a b Svante Arrhenius (1896). "On the influence of carbonic acid in the air upon the temperature of the ground". Philosophical Magazine and Journal of Science. 41 (251): 237–276. doi:10.1080/14786449608620846.
- ^ a b North, Gerald R.; Stevens, Mark J. (2006), "Energy-balance climate models", in Kiehl, J. T.; Ramanathan, V. (eds.), Frontiers in Climate Modelling, Cambridge University, p. 52, doi:10.1017/CBO9780511535857.004, hdl:2060/19810008165, ISBN 9780511535857
- ^ North, Gerald R.; Kwang-Yul, Kim (2017), Energy Balance Climate Models, Wiley Series in Atmospheric Physics and Remote Sensing, Wiley-VCH, ISBN 978-3-527-41132-0
- ^ Held, Isaac M. (2005). "The gap between simulation and understanding in climate modelling". Bulletin of the American Meteorological Society. 86 (11): 1609–1614. doi:10.1175/BAMS-86-11-1609.
- ^ Polvani, L. M.; Clement, A. C.; Medeiros, B.; Benedict, J. J.; Simpson, I. R. (2017). "When less is more: opening the door to simpler climate models". Eos (98). doi:10.1029/2017EO079417.
- ^ Goode, P. R.; et al. (2001). "Earthshine Observations of the Earth's Reflectance" (PDF). Geophys. Res. Lett. 28 (9): 1671–4. Bibcode:2001GeoRL..28.1671G. doi:10.1029/2000GL012580. S2CID 34790317. Archived (PDF) from the original on 22 July 2018.
- ^ "Scientists Watch Dark Side of the Moon to Monitor Earth's Climate". American Geophysical Union. 17 April 2001. Archived from the original on 27 February 2009. Retrieved 1 March 2010.
- ^ "Climate Change: Global Temperature". NOAA. Retrieved 6 July 2023.
- ^ "Clouds and the Earth's Radiant Energy System" (PDF). NASA. 2013. Archived from the original (PDF) on 18 February 2013.
- ^ "Seawater Samples - Emissivities". ucsb.edu.
- ^ Jin M, Liang S (15 June 2006). "An Improved Land Surface Emissivity Parameter for Land Surface Models Using Global Remote Sensing Observations" (PDF). J. Climate. 19 (12): 2867–81. Bibcode:2006JCli...19.2867J. doi:10.1175/JCLI3720.1. Archived (PDF) from the original on 4 June 2007.
- ^ T.R. Shippert; S.A. Clough; P.D. Brown; W.L. Smith; R.O. Knuteson; S.A. Ackerman. "Spectral Cloud Emissivities from LBLRTM/AERI QME" (PDF). Proceedings of the Eighth Atmospheric Radiation Measurement (ARM) Science Team Meeting March 1998 Tucson, Arizona. Archived (PDF) from the original on 25 September 2006.
- ^ A.G. Gorelik; V. Sterljadkin; E. Kadygrov; A. Koldaev. "Microwave and IR Radiometry for Estimation of Atmospheric Radiation Balance and Sea Ice Formation" (PDF). Proceedings of the Eleventh Atmospheric Radiation Measurement (ARM) Science Team Meeting March 2001 Atlanta, Georgia. Archived (PDF) from the original on 25 September 2006.
- ^ "ACS Climate Science Toolkit - Atmospheric Warming - A Single-Layer Atmosphere Model". American Chemical Society. Retrieved 2 October 2022.
- ^ "ACS Climate Science Toolkit - Atmospheric Warming - A Multi-Layer Atmosphere Model". American Chemical Society. Retrieved 2 October 2022.
- ^ "METEO 469: From Meteorology to Mitigation - Understanding Global Warming - Lesson 5 - Modelling of the Climate System - One-Layer Energy Balance Model". Pennsylvania State University College of Mineral and Earth Sciences - Department of Meteorology and Atmospheric Sciences. Retrieved 2 October 2022.
- ^ a b Manabe, Syukuro; Wetherald, Richard T. (1 May 1967). "Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity". Journal of the Atmospheric Sciences. 24 (3): 241–259. Bibcode:1967JAtS...24..241M. doi:10.1175/1520-0469(1967)024<0241:TEOTAW>2.0.CO;2.
- ^ "Syukuro Manabe Facts". nobelprize.org. Retrieved 14 November 2023.
- ^ "Pubs.GISS: Wang and Stone 1980: Effect of ice-albedo feedback on global sensitivity in a one-dimensional..." nasa.gov. Archived from the original on 30 July 2012.
- ^ Wang, W.C.; P.H. Stone (1980). "Effect of ice-albedo feedback on global sensitivity in a one-dimensional radiative-convective climate model". J. Atmos. Sci. 37 (3): 545–52. Bibcode:1980JAtS...37..545W. doi:10.1175/1520-0469(1980)037<0545:EOIAFO>2.0.CO;2.
- ^ "Energy Balance Models". shodor.org.
- ^ M.I. Budyko (1969). "The effect of solar radiation variations on the climate of the Earth". Tellus. 21 (5): 611–619. doi:10.3402/tellusa.v21i5.10109.
- ^ William D. Sellers (1969). "A Global Climatic Model Based on the Energy Balance of the Earth-Atmosphere System". Journal of Applied Meteorology. 8 (3): 392–400. Bibcode:1969JApMe...8..392S. doi:10.1175/1520-0450(1969)008<0392:AGCMBO>2.0.CO;2.
- ^ J. Graham Cogley (1990). "Twenty-five years of physical climatology". Global and Planetary Change. 2 (3–4): 213–216. doi:10.1016/0921-8181(90)90001-S.
- ^ "emics1". pik-potsdam.de.
- ^ Sarmiento, J.L.; Toggweiler, J.R. (1984). "A new model for the role of the oceans in determining atmospheric P CO 2". Nature. 308 (5960): 621–24. Bibcode:1984Natur.308..621S. doi:10.1038/308621a0. S2CID 4312683.
- ^ Norman A. Phillips (April 1956). "The general circulation of the atmosphere: a numerical experiment" (PDF). Quarterly Journal of the Royal Meteorological Society. 82 (352): 123–154. Bibcode:1956QJRMS..82..123P. doi:10.1002/qj.49708235202.
- ^ John D. Cox (2002). Storm Watchers. John Wiley & Sons, Inc. p. 210. ISBN 978-0-471-38108-2.
- ^ a b Peter Lynch (2006). "The ENIAC Integrations". The Emergence of Numerical Weather Prediction: Richardson's Dream. Cambridge University Press. p. 208. ISBN 978-0-521-85729-1. Retrieved 6 February 2018.
- ^ National Oceanic and Atmospheric Administration (22 May 2008). "The First Climate Model". Retrieved 8 January 2011.
- ^ Manabe S.; Wetherald R. T. (1975). "The Effects of Doubling the CO2 Concentration on the Climate of a General Circulation Model". Journal of the Atmospheric Sciences. 32 (3): 3–15. Bibcode:1975JAtS...32....3M. doi:10.1175/1520-0469(1975)032<0003:teodtc>2.0.co;2.
- ^ "CAM 3.1 Download". www.cesm.ucar.edu. Retrieved 25 June 2019.
- ^ William D. Collins; et al. (June 2004). "Description of the NCAR Community Atmosphere Model (CAM 3.0)" (PDF). University Corporation for Atmospheric Research. Archived from the original (PDF) on 26 September 2019. Retrieved 3 January 2011.
- ^ "CAM3.0 COMMUNITY ATMOSPHERE MODEL". University Corporation for Atmospheric Research. Retrieved 6 February 2018.
- ^ Yongkang Xue & Michael J. Fennessey (20 March 1996). "Impact of vegetation properties on U. S. summer weather prediction" (PDF). Journal of Geophysical Research. 101 (D3): 7419. Bibcode:1996JGR...101.7419X. CiteSeerX 10.1.1.453.551. doi:10.1029/95JD02169. Archived from the original (PDF) on 10 July 2010. Retrieved 6 January 2011.
- ^ "Climate Models and Their Evaluation" (PDF). Archived from the original (PDF) on 22 September 2010. Retrieved 29 August 2010.
- ^ "U.S. National Research Council Report, A National Strategy for Advancing Climate Modeling". Archived from the original on 3 October 2012. Retrieved 18 January 2021.
- ^ "U.S. National Research Council Report-in-Brief, A National Strategy for Advancing Climate Modeling". Archived from the original on 18 October 2012. Retrieved 3 October 2012.
- ^ a b Loft, Richard (2020). "Earth System Modeling Must Become More Energy Efficient". Eos (101). doi:10.1029/2020EO147051. ISSN 2324-9250.
- ^ Trader, Tiffany (2021). "Frontier to Meet 20MW Exascale Power Target Set by DARPA in 2008". HPCwire. Retrieved 8 December 2023.
- ^ "Cloud-resolving climate model meets world's fastest supercomputer". LabNews. Retrieved 8 December 2023.
External links
[edit]- Why results from the next generation of climate models matter CarbonBrief, Guest post by Belcher, Boucher, Sutton, 21 March 2019
Climate models on the web:
- NCAR/UCAR Community Climate System Model (CCSM)
- Do it yourself climate prediction
- Primary research GCM developed by NASA/GISS (Goddard Institute for Space Studies)
- Original NASA/GISS global climate model (GCM) with a user-friendly interface for PCs and Macs
- CCCma model info and interface to retrieve model data







