Jump to content

Energy density

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Bentogoa (talk | contribs) at 07:23, 29 April 2016 (Reverted edits by 114.143.212.138 (talk) (HG) (3.1.19)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

This article is about energy per unit volume. For energy per unit mass or energy density of foods, see specific energy.
Energy density
SI unitJ/m3
In SI base unitskg·m-1s-2
Derivations from
other quantities
U = E/V

Energy density is the amount of energy stored in a given system or region of space per unit volume or mass, though the latter is more accurately termed specific energy. Often only the useful or extractable energy is measured, which is to say that chemically inaccessible energy such as rest mass energy is ignored.[1] In cosmological and other general relativistic contexts, however, the energy densities considered are those that correspond to the elements of the stress–energy tensor and therefore do include mass energy as well as energy densities associated with the pressures described in the next paragraph.

Energy per unit volume has the same physical units as pressure, and in many circumstances is a synonym: for example, the energy density of a magnetic field may be expressed as (and behaves as) a physical pressure, and the energy required to compress a compressed gas a little more may be determined by multiplying the difference between the gas pressure and the external pressure by the change in volume. In short, pressure is a measure of the enthalpy per unit volume of a system. A pressure gradient has a potential to perform work on the surroundings by converting enthalpy until equilibrium is reached.

Introduction to energy density

There are many different types of energy stored in materials, and it takes a particular type of reaction to release each type of energy. In order of the typical magnitude of the energy released, these types of reactions are: nuclear, chemical, electrochemical, and electrical.

Chemical reactions are used by animals to derive energy from food, and by automobiles to derive energy from gasoline. Electrochemical reactions are used by most mobile devices such as laptop computers and mobile phones to release the energy from batteries.

Energy densities of common energy storage materials

The following is a list of the thermal energy densities of commonly used or well-known energy storage materials; it doesn't include uncommon or experimental materials. Note that this list does not consider the mass of reactants commonly available such as the oxygen required for combustion or the energy efficiency in use.

The following unit conversions may be helpful when considering the data in the table: 1 MJ ≈ 0.28 kWh ≈ 0.37 HPh.

Storage material Energy type Specific energy (MJ/kg) Energy density (MJ/L) Direct uses
Uranium (in breeder) Nuclear fission 80,620,000[2] 1,539,842,000 Electric power plants (nuclear reactors), industrial process heat (to drive chemical reactions, water desalination, etc.)
Thorium (in breeder) Nuclear fission 79,420,000[2] 929,214,000 Electric power plants (nuclear reactors), industrial process heat
Plutonium Nuclear decay 2,239,000 ? Thermal-Electric Generator (Space)
Tritium Nuclear decay 583,529 ? Electric power plants (nuclear reactors), industrial process heat
Hydrogen (compressed at 700 bar) Chemical 142 5.6 Rocket engines, automotive engines, grid storage & conversion
Methane or natural gas Chemical 55.5 0.0364 Cooking, home heating, automotive engines
Diesel / Fuel oil Chemical 48 35.8 Automotive engines, power plants[3]
LPG (including Propane / Butane) Chemical 46.4 26 Cooking, home heating, automotive engines, lighter fluid
Jet fuel (Kerosene) Chemical 46[citation needed] 37.4 Aircraft
Gasoline (petrol) Chemical 46.4 34.2 Automotive engines, power plants[4]
Fat (animal/vegetable) Chemical 37 34 Human/animal nutrition
Dimethyl ether (DME) Chemical 28.8[5] 19.3 Diesel cycle, Gas turbine, LPG applications
Ethanol fuel (E100) Chemical 26.4 20.9 Flex-fuel, racing, stoves, lighting
Coal, anthracite Chemical 26-33 34-43 Electric power plants, home heating
Coal, bituminous Chemical 24-35 26-49 Electric power plants, home heating
Methanol fuel (M100) Chemical 19.7 15.6 Racing, model engines, safety
Carbohydrates (including sugars) Chemical 17 Human/animal nutrition
Protein Chemical 16.8 Human/animal nutrition
Wood Chemical 16.2[citation needed] 13 Heating, outdoor cooking
TNT Chemical 4.6 Explosives
Gunpowder Chemical 3[citation needed] Explosives
Lithium battery (non-rechargeable) Electrochemical 1.8 4.32 Portable electronic devices, flashlights
Lithium-ion battery Electrochemical 0.36[6]–0.875[7] 0.9–2.63 Laptop computers, mobile devices, electric vehicles
Alkaline battery Electrochemical 0.5[8] 1.3[8] Portable electronic devices, flashlights
Nickel-metal hydride battery Electrochemical 0.288 0.504–1.08 Portable electronic devices, flashlights
Lead-acid battery Electrochemical 0.17 0.56 Automotive engine ignition
Supercapacitor (EDLC) Electrical (electrostatic) 0.01-0.036[9][10][11][12][13][14] 0.06-0.05[9][10][11][12][13][14] Electronic circuits
Supercapacitor (Pseudo) Electrochemical 0.031[15] 0.046[15] Electronic circuits
Electrostatic capacitor Electrical (electrostatic) 0.00001-0.0002[16] 0.00001-0.001[16][17][18] Electronic circuits
Energy capacities of common storage forms
Storage device Energy type Energy content (MJ) Typical mass Specific energy (MJ/kg) W × H × D (mm) Uses
Automotive lead-acid battery Electrochemical 2.6 15 kg 0.17 230 × 180 × 185 Automotive starter motor and accessories
Alkaline AA battery Electrochemical 0.0154 23 g 0.669 14.5 × 50.5 × 14.5 Portable electronic equipment, flashlights
Lithium-ion battery [19] Electrochemical 0.0129 20 g 0.645 54.2 × 33.8 × 5.8 Mobile phones

Energy density in energy storage and in fuel

Selected energy densities plot

In energy storage applications the energy density relates the mass of an energy store to the volume of the storage facility, e.g. the fuel tank. The higher the energy density of the fuel, the more energy may be stored or transported for the same amount of volume. The energy density of a fuel per unit mass is called the specific energy of that fuel. In general an engine using that fuel will generate less kinetic energy due to inefficiencies and thermodynamic considerations—hence the specific fuel consumption of an engine will always be greater than its rate of production of the kinetic energy of motion.

The greatest energy source by far is mass itself. This energy, E = mc2, where m = ρV, ρ is the mass per unit volume, V is the volume of the mass itself and c is the speed of light. This energy, however, can be released only by the processes of nuclear fission (.1%), nuclear fusion (1%),[citation needed] or the annihilation of some or all of the matter in the volume V by matter-antimatter collisions (100%). Nuclear reactions cannot be realized by chemical reactions such as combustion. Although greater matter densities can be achieved, the density of a neutron star would approximate the most dense system capable of matter-antimatter annihilation possible. A black hole, although denser than a neutron star, does not have an equivalent anti-particle form, but would offer the same 100% conversion rate of mass to energy in the form of Hawking radiation. In the case of relatively small black holes (smaller than astronomical objects) the power output would be tremendous.

The highest density sources of energy aside from antimatter are fusion and fission. Fusion includes energy from the sun which will be available for billions of years (in the form of sunlight) but so far (2011), sustained fusion power production continues to be elusive. Power from fission of uranium and thorium in nuclear power plants will be available for a many decades or even centuries because of the plentiful supply of the elements on earth,[20] though the full potential of this source can only be realised through breeder reactors, which are, apart from the BN-600 reactor, not yet used commercially.[21] Coal, gas, and petroleum are the current primary energy sources in the U.S.[22] but have a much lower energy density. Burning local biomass fuels supplies household energy needs (cooking fires, oil lamps, etc.) worldwide.

Energy density (how much energy you can carry) does not tell you about energy conversion efficiency (net output per input) or embodied energy (what the energy output costs to provide, as harvesting, refining, distributing, and dealing with pollution all use energy). Like any process occurring on a large scale, intensive energy use impacts the world. For example, climate change, nuclear waste storage, and deforestation may be some of the consequences of supplying our growing energy demands from hydrocarbon fuels, nuclear fission, or biomass.

No single energy storage method boasts the best in specific power, specific energy, and energy density. Peukert's Law describes how the amount of useful energy that can be obtained (for a lead-acid cell) depends on how quickly we pull it out. To maximize both specific energy and energy density, one can compute the specific energy density of a substance by multiplying the two values together, where the higher the number, the better the substance is at storing energy efficiently.

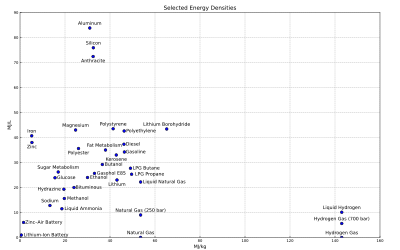
Gravimetric and volumetric energy density of some fuels and storage technologies (modified from the Gasoline article):

Note: Some values may not be precise because of isomers or other irregularities. See Heating value for a comprehensive table of specific energies of important fuels.
Note: Also it is important to realise that generally the density values for chemical fuels do not include the weight of oxygen required for combustion. This is typically two oxygen atoms per carbon atom, and one per two hydrogen atoms. The atomic weight of carbon and oxygen are similar, while hydrogen is much lighter than oxygen. Figures are presented this way for those fuels where in practice air would only be drawn in locally to the burner. This explains the apparently lower energy density of materials that already include their own oxidiser (such as gunpowder and TNT), where the mass of the oxidiser in effect adds dead weight, and absorbs some of the energy of combustion to dissociate and liberate oxygen to continue the reaction. This also explains some apparent anomalies, such as the energy density of a sandwich appearing to be higher than that of a stick of dynamite.


Energy densities ignoring external components

This table lists energy densities of systems that require external components, such as oxidisers or a heat sink or source. These figures do not take into account the mass and volume of the required components as they are assumed to be freely available and present in the atmosphere. Such systems cannot be compared with self-contained systems. These values may not be computed at the same reference conditions. Most of them seem to be higher heating value (HHV).

Energy densities of energy media
Storage type Specific energy (MJ/kg) Energy density (MJ/L) Peak recovery efficiency % Practical recovery efficiency %
Antimatter 9×10^10 = 1*c^2 (assuming c is in m/s) Density would depend on the form the antimatter takes 100
Hydrogen, liquid[23] 141.86 8.491
Hydrogen, at 690 bar and 15°C[23] 141.86 4.5
Hydrogen, gas[23] 141.86 0.01005
Diborane[24] 78.2
Beryllium 67.6 125.1
Lithium borohydride 65.2 43.4
Boron[25] 58.9 137.8
Methane (1.013 bar, 15 °C) 55.6 0.0378
Natural gas 53.6[26] 0.0364
LNG (NG at −160 °C) 53.6[26] 22.2
CNG (NG compressed to 250 bar/~3,600 psi) 53.6[26] 9
LPG propane[4] 49.6 25.3
LPG butane[4] 49.1 27.7
Gasoline (petrol)[4] 46.4 34.2
Polypropylene plastic 46.4[27] 41.7
Polyethylene plastic 46.3[27] 42.6
Crude oil (according to the definition of ton of oil equivalent) 46.3 37[26]
Residential heating oil[4] 46.2 37.3
Diesel fuel[4] 45.6 38.6
100LL Avgas 44.0[28] 31.59
Gasohol E10 (10% ethanol 90% gasoline by volume) 43.54 33.18
Lithium 43.1 23.0
Jet A aviation fuel[29]/kerosene 42.8 33
Biodiesel oil (vegetable oil) 42.20 33
DMF (2,5-dimethylfuran)[clarification needed] 42[30] 37.8
Polystyrene plastic 41.4[27] 43.5
Body fat metabolism 38 35 22[31]
Butanol 36.6 29.2
Gasohol E85 (85% ethanol 15% gasoline by volume) 33.1 25.65[citation needed]
Graphite 32.7 72.9
Coal, anthracite[32] 26-33 34-43 36
Silicon[33] 32.2 75.1
Aluminum 31.0 83.8
Ethanol 30 24
Polyester plastic 26.0[27] 35.6
Magnesium 24.7 43.0
Coal, bituminous[32] 24-35 26-49
PET plastic 23.5 (impure)[34]
Methanol 19.7 15.6
Hydrazine (toxic) combusted to N2+H2O 19.5 19.3
Liquid ammonia (combusted to N2+H2O) 18.6 11.5
PVC plastic (improper combustion toxic)[clarification needed] 18.0[27] 25.2
Wood[35] 18.0
Peat briquette[36] 17.7
Sugars, carbohydrates, and protein metabolism[citation needed] 17 26.2 (dextrose) 2222[37]
Calcium[citation needed] 15.9 24.6
Glucose 15.55 23.9
Dry cow dung and cameldung 15.5[38]
Coal, lignite[citation needed] 10-20
Sodium (burned to wet sodium hydroxide) 13.3 12.8
Sod peat 12.8
Nitromethane 11.3
Sulfur (burned to sulfur dioxide)[39] 9.23 19.11
Sodium (burned to dry sodium oxide) 9.1 8.8
Battery, lithium-air rechargeable 9.0[40]
Household waste 8.0[41]
Zinc 5.3 38.0
Iron (burned to iron(III) oxide) 5.2 40.68
Teflon plastic (combustion toxic, but flame retardant) 5.1 11.2
Iron (burned to iron(II) oxide) 4.9 38.2
ANFO 3.7
Battery, zinc-air[42] 1.59 6.02
Liquid nitrogen[clarification needed] 0.77[43] 0.62
Compressed air at 300 bar (potential energy) 0.5 0.2 >50%[citation needed]
Latent heat of fusion of ice[citation needed] (thermal) 0.335 0.335
Water at 100 m dam height (potential energy) 0.001 0.001 8585-90%[citation needed]
Storage type Energy density by mass (MJ/kg) Energy density by volume (MJ/L) Peak recovery efficiency % Practical recovery efficiency %

Divide joule metre−3 by 109 to get MJ/L. Divide MJ/L by 3.6 to get kWh/L.

Energy density of electric and magnetic fields

Electric and magnetic fields store energy. In a vacuum, the (volumetric) energy density (in SI units) is given by

where E is the electric field and B is the magnetic field. The solution will be in Joules per cubic metre. In the context of magnetohydrodynamics, the physics of conductive fluids, the magnetic energy density behaves like an additional pressure that adds to the gas pressure of a plasma.

In normal (linear and nondispersive) substances, the energy density (in SI units) is

where D is the electric displacement field and H is the magnetizing field.

See also

Footnotes

  1. ^ "The Two Classes of SI Units and the SI Prefixes". NIST Guide to the SI. Retrieved 2012-01-25.
  2. ^ a b "Computing the energy density of nuclear fuel". whatisnuclear.com. Retrieved 2014-04-17.
  3. ^ Alternative Fuels Datacenter. "Fuel Properties Comparison" (PDF). energy.gov. Retrieved 9 September 2014.
  4. ^ a b c d e f IOR Energy. List of common conversion factors (Engineering conversion factors). Retrieved 2008-10-05.
  5. ^ "F3 (Fossil Free Fuels) Centre - the Swedish Knowledge Centre for Renewable Transportation - Dimethyl Ether". October 2015.
  6. ^ "Overview of lithium ion batteries" (PDF). Panasonic. Jan 2007. Archived from the original (PDF) on Nov 7, 2011. {{cite web}}: Unknown parameter |deadurl= ignored (|url-status= suggested) (help)
  7. ^ "Panasonic NCR18650B" (PDF).
  8. ^ a b "Energizer EN91 AA alkaline battery datasheet" (PDF). Retrieved 2016-01-10.
  9. ^ a b "Maxwell supercapacitor comparision" (PDF). Retrieved 2016-01-10.
  10. ^ a b "Nesscap ESHSP series supercapacitor datasheet" (PDF). Retrieved 2016-01-10.
  11. ^ a b "Cooper PowerStor XL60 series supercapacitor datasheet" (PDF). Retrieved 2016-01-10.
  12. ^ a b "Kemet S301 series supercapacitor datasheet" (PDF). Retrieved 2016-01-10.
  13. ^ a b "Nichicon JJD series supercapatcitor datasheet" (PDF). Retrieved 2016-01-10.
  14. ^ a b "skelcap High Energy Ultracapacitor" (PDF). Skeleton Technologies. Retrieved 13 October 2015.
  15. ^ a b "Nesscap PSHLR series pseudocapacitor datasheet" (PDF). Retrieved 2016-01-10.
  16. ^ a b "Vishay STE series tantalum capacitors datasheet" (PDF). Retrieved 2016-01-10.
  17. ^ "nichicon TVX aluminum electrolytic capacitors datasheet" (PDF). Retrieved 2016-01-10.
  18. ^ "nichicon LGU aluminum electrolytic capacitors datasheet" (PDF). Retrieved 2016-01-10.
  19. ^ "Nokia BL-5C datasheet" (PDF).
  20. ^ "Supply of Uranium". world-nuclear.org. 2014-10-08. Retrieved 2015-06-13.
  21. ^ "Facts from Cohen". Formal.stanford.edu. 2007-01-26. Retrieved 2010-05-07.
  22. ^ "U.S. Energy Information Administration (EIA) - Annual Energy Review". Eia.doe.gov. 2009-06-26. Archived from the original on 2010-05-06. Retrieved 2010-05-07.
  23. ^ a b c College of the Desert, “Module 1, Hydrogen Properties”, Revision 0, December 2001 Hydrogen Properties. Retrieved 2014-06-08.
  24. ^ Greenwood, Norman N.; Earnshaw, Alan (1997), Chemistry of the Elements (2nd ed) (page 164)
  25. ^ "Boron: A Better Energy Carrier than Hydrogen? (28 February 2009)". Eagle.ca. Retrieved 2010-05-07.
  26. ^ a b c d Envestra Limited. Natural Gas. Retrieved 2008-10-05.
  27. ^ a b c d e Paul A. Kittle, Ph.D. "ALTERNATE DAILY COVER MATERIALS AND SUBTITLE D - THE SELECTION TECHNIQUE" (PDF). Retrieved 2012-01-25.
  28. ^ "537.PDF" (PDF). June 1993. Retrieved 2012-01-25.
  29. ^ "Energy Density of Aviation Fuel". Hypertextbook.com. Retrieved 2010-05-07.
  30. ^ Nature. "Production of dimethylfuran for liquid fuels from biomass-derived carbohydrates : Abstract". Nature. Retrieved 2010-05-07.
  31. ^ Justin Lemire-Elmore (2004-04-13). "The Energy Cost of Electric and Human-Powered Bicycles" (PDF). p. 5. Retrieved 2009-02-26. properly trained athlete will have efficiencies of 22 to 26%
  32. ^ a b Fisher, Juliya (2003). "Energy Density of Coal". The Physics Factbook. Retrieved 2006-08-25.
  33. ^ Silicon as an intermediary between renewable energy and hydrogen
  34. ^ "Elite_bloc.indd" (PDF). Retrieved 2010-05-07.
  35. ^ "Biomass Energy Foundation: Fuel Densities". Woodgas.com. Archived from the original on 2010-01-10. Retrieved 2010-05-07.
  36. ^ "Bord na Mona, Peat for Energy" (PDF). Bnm.ie. Archived from the original (PDF) on 2007-11-19. Retrieved 2012-01-25.
  37. ^ Justin Lemire-Elmor (April 13, 2004). "The Energy Cost of Electric and Human-Powered Bicycle" (PDF). Retrieved 2012-01-25.
  38. ^ "energy buffers". Home.hccnet.nl. Retrieved 2010-05-07.
  39. ^ Anne Wignall and Terry Wales. Chemistry 12 Workbook, page 138. Pearson Education NZ ISBN 978-0-582-54974-6
  40. ^ Mitchell, Robert R.; Betar M. Gallant; Carl V. Thompson; Yang Shao-Horn (2011). "All-carbon-nanofiber electrodes for high-energy rechargeable Li–O2 batteries". Energy & Environmental Science. 4: 2952–2958. doi:10.1039/C1EE01496J.
  41. ^ David E. Dirkse. energy buffers. "household waste 8..11 MJ/kg"
  42. ^ "Technical bulletin on Zinc-air batteries". Duracell. Archived from the original on 2009-01-27. Retrieved 2009-04-21.
  43. ^ C. Knowlen, A.T. Mattick, A.P. Bruckner and A. Hertzberg, "High Efficiency Conversion Systems for Liquid Nitrogen Automobiles", Society of Automotive Engineers Inc, 1988.

Density data

  • ^ "Aircraft Fuels." Energy, Technology and the Environment Ed. Attilio Bisio. Vol. 1. New York: John Wiley and Sons, Inc., 1995. 257–259
  • "Fuels of the Future for Cars and Trucks" - Dr. James J. Eberhardt - Energy Efficiency and Renewable Energy, U.S. Department of Energy - 2002 Diesel Engine Emissions Reduction (DEER) Workshop San Diego, California - August 25–29, 2002

Energy storage

Books

  • The Inflationary Universe: The Quest for a New Theory of Cosmic Origins by Alan H. Guth (1998) ISBN 0-201-32840-2
  • Cosmological Inflation and Large-Scale Structure by Andrew R. Liddle, David H. Lyth (2000) ISBN 0-521-57598-2
  • Richard Becker, "Electromagnetic Fields and Interactions", Dover Publications Inc., 1964
Retrieved from "https://en.wikipedia.org/w/index.php?title=Energy_density&oldid=717704029"