Energy

Lightning is the electric breakdown of air by strong electric fields (from electric potential energy to mechanical energy of the random motion of air molecules (heat), and to light).

For other uses of "energy" see Energy.

In physics and other sciences, energy (from the Greek ενεργός, energos, "active, working") is a concept, a quantifiable attribute of physical systems. It is not an object or a substance, but it is quantifiable in a way such that it cannot be created or destroyed. The units used to quantitate energy are the same as those used to define work in physics. Many forms of energy are defined in the natural sciences, e.g. kinetic energy, potential energy, electrical energy; chemical energy etc.; any one of them can be transformed into another form, often through a process that involves mechanical work. However, the transformation from one form to another is not always total, it is limited by the second law of thermodynamics. A fraction of the energy remains in the form of thermal energy in many such transformations.

Definitions

Energy, in physics, can be defined as the amount of work a physical system can do on another. In this way, energies such as gravitational energy, electric energy, and elastic energy can be defined from the work done by different types of forces.

Some textbooks prefer to introduce energy without relying on prior definitions of force, work, or momentum.

Historical perspective

Main articles: Timeline of thermodynamics, statistical mechanics, and random processes and History of Physics

Thomas Young - the first to use the term "energy" in the modern sense.

The concept of energy emerged out of the idea of vis viva, which Leibniz defined as the product of the mass of an object and its velocity squared; he believed that total vis viva was conserved. To account for slowing due to friction, Leibniz claimed that heat consisted of the random motion of the constituent parts of matter — a view shared by Isaac Newton, although it would be more than a century until this was generally accepted. In 1807, Thomas Young was the first to use the term "energy", instead of vis viva, in its modern sense. Gustave-Gaspard Coriolis described "kinetic energy" in 1829 in its modern sense, and in 1853, William Rankine coined the term "potential energy."

The development of steam engines required engineers to develop concepts and formulas that would allow them to describe the mechanical and thermal efficiencies of their systems. Engineers such as Sadi Carnot, physicists such as James Prescott Joule, mathematicians such as Émile Clapeyron and Hermann von Helmholtz , and amateurs such as Julius Robert von Mayer all contributed to the notion that the ability to perform certain tasks, called work, was somehow related to the amount of energy in the system. The nature of energy was elusive, however, and it was argued for some years whether energy was a substance (the caloric) or merely a physical quantity, such as momentum.

William Thomson (Lord Kelvin) amalgamated all of these laws into the laws of thermodynamics, which aided in the rapid development of explanations of chemical processes using the concept of energy by Rudolf Clausius, Josiah Willard Gibbs and Walther Nernst. It also led to a mathematical formulation of the concept of entropy by Clausius, and to the introduction of laws of radiant energy by Jožef Stefan.

During a 1961 lecture for undergraduate students at the California Institute of Technology, Richard Feynman, a celebrated physics teacher and Nobel Laureate, said this about the concept of energy:

There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.

— The Feynman Lectures on Physics

Since 1918 it has been known that the law of conservation of energy is the direct mathematical consequence of the translational symmetry of the quantity conjugate to energy, namely time. That is, energy is conserved because the laws of physics do not distinguish between different moments of time (see Noether's theorem).

Energy in various contexts

The concept of energy and its transformations is extremely useful in explaining and predicting most natural phenomena. The direction of transformations in energy (what kind of energy is transformed to what other kind) is often directed by entropy (energy spread) considerations, since in practice all energy transformations are permitted on a small scale, but certain larger transformations are not permitted because it is statistically unlikely that energy or matter will randomly move into more concentrated forms or smaller spaces.

The concept of energy is often used in almost all fields of science. For example, in Chemistry, Biology, Geology and Meterology The exact context of various natural phenomena associated with these transformations varies from one natural science to another.

Regarding applications of energy concept

Energy is subject to a strict global conservation law; that is, whenever one measures (or calculates) the total energy of a system of particles whose interactions do not depend explicitly on time, it is found that the total energy of the system always remains constant

• The total energy of a system can be subdivided and classified in various ways. For example, it is sometimes convenient to distinguish potential energy (which is a function of coordinates only) from kinetic energy (which is a function of coordinate time derivatives only). It may also be convenient to distinguish gravitational energy, electrical energy, thermal energy, and other forms. These classifications overlap; for instance thermal energy usually consists partly of kinetic and partly of potential energy.
• The transfer of energy can take various forms; familiar examples include work, heat flow, and advection, as discussed below.
• The word "energy" is also used outside of physics in many ways, which can lead to ambiguity and inconsistency. The vernacular terminology is not consistent with technical terminology. For example, the important public-service announcement, "Please conserve energy" uses vernacular notions of "conservation" and "energy" which make sense in their own context but are utterly incompatible with the technical notions of "conservation" and "energy" (such as are used in the law of conservation of energy)..

In classical physics energy is considered a scalar quantity, canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy-momentum 4-vector). In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of space-time (= boosts).

Energy transfer

Because energy is strictly conserved and is also locally conserved (wherever it can be defined), it is important to remember that by definition of energy the transfer of energy between the "system" and adjacent regions is work. A familiar example is mechanical work. In simple cases this is written as:

$\Delta {}E=W$             (1)

if there are no other energy-transfer processes involved. Here $\Delta {}E$  is the amount of energy transferred, and $W$  represents the work done on the system.

More generally, the energy transfer can be split into two categories:

$\Delta {}E=W+Q$             (2)

where $Q$  represents the heat flow into the system.

There are other ways in which an open system can gain or lose energy. If mass if counted as energy (as in many relativistic problems) then E must contain a term for mass lost or gained. In chemical systems, energy can be added to a system by means of adding substances with different chemical potentials, which potentials are then extracted (both of these process are illustrated by fueling an auto, a system which gains in energy thereby, without addition of either work or heat). These terms may be added to the above equation, or they can generally be subsumed into a quantity called "energy addition term E" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).

$\Delta {}E=W+Q+E$             (3)

Where E in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.

Energy is also transfered from potential energy (E_p) to kinetic energy (E_k) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy can not be created or destroyed, so the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:

E_pi + E_ki = E_pf + E _kf

The equation can then be simplified further since E_p = mgh (mass times acceleration due to gravity times the height) and E_k = 1/2 mv² (half times mass times velocity squared). Then the total amount of energy can be found by adding E_p + E_k = E_total.

The Hamiltonian

The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.

The Lagrangian

Another energy-related concept is called the Lagrangian, after Joseph Louis Lagrange. This is in some ways even more fundamental than the Hamiltonian, and can be used to derive the equations of motion. In simple cases the Lagrangian can be written as kinetic energy minus potential energy.

Usually Lagrange formalism is mathematically more convenient than Hamilton one for non-conservative systems (like systems with friction).

Energy and thermodynamics

According to the second law of thermodynamics, work can be totally converted into heat, but not vice versa. The first law of thermodynamics simply asserts that energy is conserved, and that heat is included as a form of energy transfer. A commonly-used corollary of the first law is that for a "system" subject only to pressure forces and heat transfer (e.g. a cylinder-full of gas), the change in energy of the system is given by:

$\mathrm {d} E=T\mathrm {d} S-P\mathrm {d} V\,$,

where the first term on the right is the heat transfer, defined in terms of temperature T and entropy S, and the last term on the right hand side is identified as "work" done on the system, where pressure is P and volume V (the negative sign is because we must compress the system to do work on it, so that the volume change dV is negative). Although the standard text-book example, this is very specific, ignoring all chemical, electrical, nuclear, and gravitational forces, effects such as advection, and because it depends on temperature. The most general statement of the first law — i.e. conservation of energy — is valid even in situations in which temperature is undefinable.

Energy is sometimes expressed as:

$\mathrm {d} E=\delta Q+\delta W\,$,

which is unsatisfactory because there cannot exist any thermodynamic state functions W or Q that are meaningful on the right hand side of this equation, except perhaps in trivial cases.

Equipartition of energy

The energy of a mechanical harmonic oscillator (a mass on a spring) is alternatively kinetic and potential. At two points in the oscillation cycle it is entirely kinetic, and alternatively at two other points it is entirely potential. Over the whole cycle, or over many cycles net energy is thus equally split between kinetic and potential. This is called equipartition principle - total energy of a system with many degrees of freedom is equally split between all these degrees of freedom.

This principle is vitally important to understanding the behavior of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. This concept is also related to the second law of thermodynamics which basically states that when an isolated system is given more degrees of freedom (places where energy may be stored), energy spreads evenly over all allowed degrees (without distinction between "new" and "old" degrees).

Oscillators, phonons, and photons

In an ensemble of unsynchronized oscillators, the average energy is spread equally between kinetic and potential.

In a solid, thermal energy (often referred to as heat) can be accurately described by an ensemble of thermal phonons that act as mechanical oscillators. In this model, thermal energy is equally kinetic and potential.

In ideal gas, potential of interaction between particles is essentially delta function - thus all of the energy is kinetic.

Because an electrical oscillator (LC circuit) is analogous to a mechanical oscillator, its energy must be, on average, equally kinetic and potential. It is entirely arbitrary whether the magnetic energy is considered kinetic and the electrical energy considered potential, or vice versa. That is, either the inductor is analogous to the mass while the capacitor is analogous to the spring, or vice versa.

1. By extension of the previous line of thought, in free space the electromagnetic field can be considered an ensemble of oscillators, meaning that radiation energy can be considered equally potential and kinetic. This model is useful, for example, when the electromagnetic Lagrangian is of primary interest and is interpreted in terms of potential and kinetic energy.
2. On the other hand, in the key equation $m^{2}c^{4}=E^{2}-p^{2}c^{2}$, the contribution $mc^{2}$ is called the rest energy, and all other contributions to the energy are called kinetic energy. For a particle that has mass, this implies that the kinetic energy is $0.5p^{2}/m$ at speeds much smaller than c, as can be proved by writing $E=mc^{2}$ √$(1+p^{2}m^{-2}c^{-2})$ and expanding the square root to lowest order. By this line of reasoning, the energy of a photon is entirely kinetic, because the photon is massless and has no rest energy. This expression is useful, for example, when the energy-versus-momentum relationship is of primary interest.

The two analyses are entirely consistent. The electric and magnetic degrees of freedom in item 1 are transverse to the direction of motion, while the speed in item 2 is along the direction of motion. For non-relativistic particles these two notions of potential versus kinetic energy are numerically equal, so the ambiguity is harmless, but not so for relativistic particles.

Work and virtual work

Main articles: Mechanics, Mechanical work, Thermodynamics, and Quantum mechanics

Work is roughly force times distance. But more precisely, it is

$W=\int \mathbf {F} \cdot \mathrm {d} \mathbf {s}$

This says that the work ($W$) is equal to the integral (along a certain path) of the force; for details see the mechanical work article.

Work is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.

Quantum mechanics

In quantum mechanics energy is defined in terms of the energy operator as a time derivative of the wave function.

As the Schrödinger equation (which equates energy operator to full energy of a particle or a system) describes the space- and time-dependence of quantum mechanical systems and bound systems the solution of this equation is discrete (a set of permitted states, each characterized by an energy level). In quantum wave mechanics energy is related to the frequency of the wave by the Planck equation $E=h\nu$ (where $h$ is the Planck's constant and $\nu$ the frequency).

Relativity

According to special relativity, rest mass is a part of total energy as can be seen from the relativistic equation relating mass, energy and momentum of a body:

$m^{2}c^{4}=E^{2}-p^{2}c^{2}$,

where

m is the mass,

c is the speed of light,

E is the energy, and

p is the 3-dimensional momentum.

This equation is a mathematical by-product of calculation of relativistic work to accelerate a body (=calculation of relativistic kinetic energy).

For example, consider electron-positron annihilation, in which the rest mass of individual particles is destroyed, but the inertia equivalent of the system of the two particles (its invariant mass) remains (since all energy is associated with mass), and this inertia and invariant mass is carried off by photons which individually are massless, but as a system retain their mass. This is a reversible process - the inverse process is called pair creation - in which the rest mass of particles is created from energy of two (or more) annihilating photons.

In general relativity, the stress-energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.

It is a common misconception to assert that energy is "equivalent" to mass. It would be more accurately to state that energy has inertia and gravity equivalent, and because mass is a form of energy, then mass too has inertia and gravity associated with it.

That misconception presumably arises from trying to reconcile the conservation law with a pre-20th-century definition of energy. In the modern view, the rest energy (aka mass) is included in the definition of energy. Therefore the relevant conservation law is as simple as can be: E is conserved.

Astronomy and cosmology

The phenomona of stars, nova, supernova, quasars and gamma ray bursts are the universe's highest-output energy transformations of matter. All stellar phenomena (including solar activity) are driven by various kinds of energy transformations. Energy in such transformations is either from gravitational collapse of matter (usually molecular hydrogen) into various classes of astronomical objects (stars, black holes, etc.), or from nuclear fusion (of lighter elements, primarily hydrogen).

Dark energy is believed to make up 70% of the universe

Light elements, primarily hydrogen and helium, were created in the Big Bang. These light elements were spread too fast and too thinly in the Big Bang process (see nucleosynthesis) to form the most stable medium-sized atomic nuclei, like iron and nickel. This fact allows for later energy release, as such intermediate-sized elements are formed in our era. The formation of such atoms powers the steady energy-releasing reactions in stars, and also contributes to sudden energy releases, such as in novae. Gravitational collapse of matter into black holes is also thought to power the very most energetic processes, generally seen at the centers of galaxies (see quasars and in general active galaxies).

Cosmologists are still unable to explain all cosmological phenomena purely on the basis of known conventional forms of energy, for example those related to the accelerating expansion of the universe, and therefore invoke a yet unexplored form of energy called dark energy to account for certain cosmological observations. One hypothesis is that dark energy is the energy of virtual particles (which mathematically must exist in vacuum due to the uncertainty principle).

There is no unambiguous way to define the total energy of the universe in the current best theory of gravity, general relativity. As a result it remains controversial whether one can meaningfully say that total energy is conserved in an expanding universe. For instance, each photon that travels through intergalactic space loses energy due to the redshift effect. This energy is not obviously transferred to any other system, so seems to be permanently lost. Nevertheless some cosmologists insist that energy is conserved in some sense.

Measurement

There is no absolute measure of energy. Rather energy is measured in terms of the transition of a system from one state into another.

Methods

The methods for the measurement of energy often deploy methods for the measurement of still more fundamental concepts of science, viz. mass, distance, radiation, temperature, time, electric charge and electric current.

A Calorimeter - An instrument used by physicists to measure energy

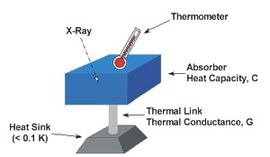
Conventionally the technique most often employed are calorimetry, in thermodynamics that relies on the measurement of temperature: a thermometer or a bolometer for measurement of intensity of a radiation.

Units

Main article: Units of energy

Through the history of science energy has been expressed in several different units, e.g. ergs and calorie. At present, the accepted unit of measurement for energy is the SI unit of energy is the joule.

Kinetic and potential energy

Main articles: Kinetic energy, Potential energy, Electromagnetic radiation, Photon, and Thermal energy

Classical kinetic energy is due to motion of a body, or particles within it (subject to length-scale restrictions, as discussed below).

Classical potential energy is due to the position of an object relative to other objects. This form of energy can be positive or negative, depending on whether it is work done on an object by a force, or work done by the object against a force. Negative energy is a thus a mathematical construct in reference to another system. Each of the fundamental interactions of nature can be linked to a kind of potential energy.

These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopic potential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy (below) is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.

— 

Forms of energy

Heat, a form of energy, is partly potential energy and partly kinetic energy.

In the context of natural sciences, energy can be in any of several different forms: thermal, chemical, electrical, radiant, nuclear etc. Some basic textbooks broadly groups all these forms of energy into two broad categories: kinetic energy and potential energy. However, some forms of energy resist such easy classification, as is the case with light energy. Other familiar types of energy (such as heat in most circumstances) are a varying mix of both potential and kinetic energy.

Gravitational potential energy

Gravitational potential energy is the work of gravitational force during rearrangement of mutual positions of interacting masses - say, when masses are moved apart (such as when a crate is lifted), or closer together (as when a meteorite falls to Earth). If the masses of the objects are considered to be point masses, this work (thus the gravitational potential energy) is equal to

$E_{pG}=-{GmM \over r}$

where

m and M are the two masses in question,

r is the distance between them,

G is the gravitational constant.

Electric potential energy

Electric potential energy is the work of electric forces during rearrangement of positions of charges (usually versus some reference configuration of the same charges - say, charges at infinite distance from each other). This energy results in chemical potential energies (energy required to break chemical bonds, or obtained from forming them). Energy per unit of electric charge is called potential. Chemical potentials can be seen directly in the electrical potentials of electrochemical cell (grouped in batteries), and fuel cells. The energy released in lightning, from burning a liter of fuel oil, or from using an amount of electrical power from an electrical-wiring system, are all common examples of extracting work from rearrangement of charges, which is stored beforehand as electromagnetic potential energy. Spatially it is stored in the electric field surrounding charges. Quantitatively, electromagnetic potential energy is:

$E_{pE}={qQ \over 4\pi \epsilon _{0}r}$

where

q and Q are the electric charges on the objects in question,

r is the distance between them,

ε₀ is the electric constant of a vacuum.

In use of electrical energy from an electrical wiring system, or from a chemical battery, the electric potential energy available per amount of electric charge moved (which in turn is given by electric current multiplied by time), is represented by the electrical potential difference (measured in volts) between the conductors. Thus, when one ampere flows for one second across a potential of one volt, one joule of energy is made available from the electrical potential. The force which provides for the work that is done, is provided to the charge by an electrical field.

Magnetic energy

Energy can also be stored in a magnetic field. Certain particles having spinning charge generate magnetic field in their vicinity. Electric current in superconducting magnetic energy storage generates strong magnetic field which has energy associated with it - and thus electromagnet can be used to store energy. Since magnetic field is simply relativistic part of electric field, magnetic energy is closely related to electric energy. Variable magnetic field generating variable electric field results in transfer of energy (thus, of power) by an electrical transformer.

Thermal potential energy

Potential thermal energy is the part of thermal energy which is not made up of kinetic thermal energy, and is thus stored as electric potential energy. This potential electrical part of thermal energy is stored in "deformation" of atomic bonds during thermal motion of atoms (as atoms oscillate around their position of equilibrium, they not only have kinetic energy of motion, but also a potential energy of displacement from equilibrium). This type of potential energy is a significant portion (about half) of thermal energy for strongly-bonded systems (solids and liquids), with the rest of thermal energy in such systems being the kinetic energy of the atoms.

In monoatomic gas, however, the potential part of thermal energy is a smaller fraction of thermal energy in gases (as gas molecules practically do not interact with each other) - thus almost all their thermal energy is kinetic.

In multiatomic gases vibrational energy has its potential part U=nkT/2 where n is the number of vibrational degrees of freedom.

Each existing degree of freedom in physical system (say, gas molecule) contributes equal amount kT/2 into total thermal energy.

Chemical potential energy

Potential chemical energy of an object is the energy which may potentially be liberated as a result of transformations of chemical substances it is composed of.

The change in chemical potential energy in the course of a chemical transformation depends on the parameters like temperature, pressure and concentration. It is equal to the difference between the energy content of the product substances and that of the reactants. Energy is involved in breaking or making of chemical bonds. Some energy can be released as a result of rearrangement of bonds between atoms of a chemical substance (or a mixture thereof) only if the energy in the reactant chemical substances is more than that in product substances.

This change in energy is rigorously the change in internal energy. It can be calculated using the formula

ΔU^o = Σ(ΔU_f^o_products) - Σ(ΔU_f^o_reactants).

Where ΔU_f^o_reactants is the internal energy of formation of the reactant molecules that can be calculated from the bond energies of the various chemical bonds of the molecules under consideration and ΔU_f^o_products is the internal energy of formation of the product molecules. The internal energy change of a process is equal to the heat change if it is measured under conditions of constant volume, as in a closed rigid container such as a bomb calorimeter. Under conditions of constant pressure, as in reactions in vessels open to the atmosphere, the heat change measured is not always the same as the internal energy change, since pressure-volume work releases or absorbs heat and energy. (The heat change at constant pressure is called the enthalpy change, in this case the enthalpy of formation).

The mixture of a hydrocarbon fuel and oxygen is an example: the hydrocarbon and oxygen molecules contain more energy in their C-H, C-C, and O-O bonds compared to the O-H and C-O bonds of the products of combustion (water and carbon dioxide). All chemical bonds represent missing energy; it takes energy to break ALL of them. Still, energy storage in chemical systems may be accomplished by making and breaking bonds: if net energy used in breaking bonds during a reaction is exceeded by energy released in making new bonds, energy will be released.

The chemical potential energy of a fuel appears as its heat of combustion. Food is similar to hydrocarbon fuel and carboydrate fuels, and when it is oxidized, its caloric content is similar (though not assessed in the same way as a hydrocarbon fuel-- see food energy).

Some chemical fuels or explosives (for example, nitroglycerine) do not require a second reactant substance to release their potential chemical energy, but even in these cases, the source of the energy released is the difference in the net difference in total strengths of the chemical bonds between the products and the reactants.

Another common form of chemical potential exists in batteries, but here again bonds are broken, and a standard chemical reaction occurs in which electrons are transferred from one atom to another, along an electrical potential (voltage gradient).

In chemical thermodynamics the term used for the chemical potential energy is chemical potential and for chemical transformation an equation most often used is Gibbs-Duhem equation

$\sum _{i}N_{i}\mathrm {d} \mu _{i}=-S\mathrm {d} T+V\mathrm {d} P\,$

Elastic potential energy

Potential elastic energy is the energy stored in the elastic intermolecular bonds. Elastic energy is actually of several types: it is sometimes a kind of electric potential energy (as in metal springs), and in these cases energy is released as charged atoms which have been compressed are allowed to move apart. However, in other cases (such as compressed ideal gas) the potential energy is not stored as electric, but rather is stored as a kinetic energy of moving atoms.

In the ideal case of a metal spring described by Hooke's Law, the stored elastic energy is equal to:

$\!E_{pE}={{\frac {1}{2}}kx^{2}}$

where

k is the spring constant, dependent on the individual spring,

x is the deformation of the object.

Nuclear potential energy

Nuclear potential energy, along with electric potential energy, provides the energy released from nuclear fission and nuclear fusion processes. The result of both these processes are nuclei in which strong nuclear forces bind nuclear particles more strongly and closely. Weak nuclear forces (different from strong forces) provide the potential energy for certain kinds of radioactive decay, such as beta decay. The energy released in nuclear processes is so large that the relativistic change in mass (after the energy has been removed) can be as much as several parts per thousand.

Nuclear particles like protons and neutrons are not destroyed(law of conservation of energy) in fission and fusion processes (except in beta minus and beta plus decay or electron capture decay), but collections of them have less mass than if they were individually free, and this mass difference is liberated as heat and radiation in nuclear reactions (the heat and radiation have the missing mass, but it often escapes from the system, where it is not measured). The energy from the Sun, also called solar energy, is an example of this form of energy conversion. In the Sun, the process of hydrogen fusion converts about 4 million metric tons of solar matter per second into light, which is radiated into space. In this system, the light itself retains the inertia equivalent of this mass, and indeed the mass itself (as a system) and represents 4 million tons per second of electromagnetic field, moving into space.

Transformations of energy

Main article: Energy conversion

One form of energy can often be readily transformed into another with the help of a device- for instance, a battery, from chemical energy to electrical energy; a dam: gravitational potential energy to kinetic energy of moving water (and the blades of a turbine) and ultimately to electric energy through an electrical generator. Similarly, in the case of a chemical explosion, chemical potential energy is transformed to kinetic energy and thermal energy in a very short time. Yet another example is that of a pendulum. At its highest points the kinetic energy is zero and the gravitational potential energy is at maximum. At its lowest point the kinetic energy is at maximum and is equal to the decrease of potential energy. If one (unrealistically) assumes that there is no friction, the conversion of energy between these processes is perfect, and the pendulum will continue swinging forever.

Energy can be converted into matter and vice versa. The mass-energy equivalence formula E = mc², derived independently by Albert Einstein and Henri Poincaré, quantifies the relationship between mass and rest energy. Since $c^{2}$ is very large relative to ordinary human scales, the conversion of mass to other forms of energy can liberate tremendous amounts of energy, as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why loss of energy from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (particles) are found in high energy nuclear physics.

In nature, transformations of energy can fundamentally classed into two kinds: those that are thermodynamically reversible, and those that are thermodynamically irreversible. A reversible process in thermodynamics is one in which no energy is dissipated into empty quantum states available in a volume, from which it cannot be recovered into more concentrated forms (fewer quantum states), without degradation of even more energy. A reversible process is one in which this sort of dissipation does not happen. For example, conversion of energy from one type of potential field to another, is reversible, as in the pendulum system described above. In processes where heat is generated, however, quantum states of lower energy, present as possible exitations in fields between atoms, act as a reservoir for part of the energy, from which it cannot be recovered, in order to be converted with 100% efficiency into other forms of energy. In this case, the energy must partly stay as heat, and cannot be completely recovered as usable energy, except at the price of an increase in some other kind of heat-like increase in disorder in quantum states, in the universe (such as an expansion of matter, or a randomization in a crystal).

As the universe evolves in time, more and more of its energy becomes trapped in irreversible states (i.e., as heat or other kinds of increases in disorder). This has been referred to as the inevitable thermodynamic heat death of the universe. In this heat death the energy of the universe does not change, but the fraction of energy which is available to do work, or be transformed to other usable forms of energy, grows less and less.

Law of conservation of energy

Main article: Conservation of energy

Energy is subject to the law of conservation of energy. According to this law, energy can neither be created (produced) nor destroyed. It can only be transformed.

Most kinds of energy (with gravitational energy being a notable exception)[1] are also subject to strict local conservation laws, as well. In this case, energy can only be exchanged between adjacent regions of space, and all observers agree as to the volumetric density of energy in any given space. There is also a global law of conservation of energy, stating that the total energy of the universe cannot change; this is a corollary of the local law, but not vice versa. Conservation of energy is the mathematical consequence of translational symmetry of time (=indistinguishability of time intervals taken at different time) - see Noether's theorem.

According to energy conservation law the total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system.

This law is a fundamental principle of physics. It follows from the translational symmetry of time, a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable.

Because energy is quantity which is canonical conjugate to time, it is impossible to define exact amount of energy during any finite time interval - making it impossible to apply the law of conservation of energy. This must not be considered a "violation" of the law. We know the law still holds, because a succession of short time periods does notaccumulate any violation of conservation of energy.

In quantum mechanics energy is expressed using the Hamiltonian operator. On any time scales, the uncertainty in the energy is by

$\Delta E\Delta t\geq {\frac {h}{4\pi }}$

which is similar in form to the uncertainty principle (but not really mathematically equivalent thereto, since H and t are not dynamically conjugate variables, neither in classical nor in quantum mechanics).

In particle physics, this inequality permits a qualitative understanding of virtual particles which carry momentum, exchange by which with real particles is responsible for creation of all known fundamental forces (more accurately known as fundamental interactions). Virtual photons (which are simply lowest quantum mechanical energy state of photons) are also responsible for electrostatic interaction between electric charges (which results in Coulomb law), for spontaneous radiative decay of exited atomic and nuclear states, for the Casimir force, for van der Waals bond forces and some other observable phenomena.

See also

• Activation energy
• Enthalpy
• Energy(Chemistry)
• Energy(Biology)
• Energy(Earth Sciences)
• Energy policy
• Energy: world resources and consumption
• Free energy
• Interaction energy
• Internal energy
• Negative energy
• Orders of magnitude (energy)
• Power (physics)
• Renewable energy
• Solar radiation
• Thermodynamic entropy
• Thermodynamics
• Units of energy measurements

Notes and references

Other books

• Alekseev, G. N. (1986). Energy and Entropy. Moscow: Mir Publishers.
• Walding, Richard,  Rapkins, Greg,  Rossiter, Glenn (1999-11-01). New Century Senior Physics. Melbourne, Australia: Oxford University Press. ISBN 0-19-551084-4.{{cite book}}: CS1 maint: multiple names: authors list (link)

External links

• A forum discussion among physicsts on the definition of energy
• Conservation of Energy - a chapter from an online textbook
• Template:PDFlink on Project PHYSNET
• Freeview video 'Endless Energy' scientists discuss renewable energy. A programme by the Vega Science Trust and the BBC/OU
• What does energy really mean? From Physics World
• Compact description of various energy sources. Energy sources and ecology.
• World Energy Education Foundation
• Glossary of Energy Terms
• International Energy Agency IEA - OECD
• Energy & Environmental Security
• Energy for kids
• Energy riddle and transformations