Dodecahedron

Template:Reg polyhedron stat table In geometry, a dodecahedron (Greek δωδεκάεδρον, from δώδεκα, dōdeka "twelve" + ἕδρα hédra "base", "seat" or "face") is any polyhedron with twelve flat faces, but usually a regular dodecahedron is meant: a Platonic solid. It is composed of 12 regular pentagonal faces, with three meeting at each vertex, and is represented by the Schläfli symbol {5,3}. It has 20 vertices, 30 edges and 160 diagonals. Its dual polyhedron is the icosahedron, with Schläfli symbol {3,5}.

A large number of other (nonregular) polyhedra also have twelve faces, most notably the topologically identical pyritohedron with tetrahedral symmetry, and the rhombic dodecahedron with octahedral symmetry.

Dimensions

If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the dodecahedron at all vertices) is

$r_{u}=a{\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\approx 1.401258538\cdot a$ OEIS: A179296

and the radius of an inscribed sphere (tangent to each of the dodecahedron's faces) is

$r_{i}=a{\frac {1}{2}}{\sqrt {{\frac {5}{2}}+{\frac {11}{10}}{\sqrt {5}}}}\approx 1.113516364\cdot a$

while the midradius, which touches the middle of each edge, is

$r_{m}=a{\frac {1}{4}}\left(3+{\sqrt {5}}\right)\approx 1.309016994\cdot a$

These quantities may also be expressed as

$r_{u}=a\,{\frac {\sqrt {3}}{2}}\varphi$

$r_{i}=a\,{\frac {\varphi ^{2}}{2{\sqrt {3-\varphi }}}}$

$r_{m}=a\,{\frac {\varphi ^{2}}{2}}$

where φ is the golden ratio.

Note that, given a regular pentagonal dodecahedron of edge length one, r_u is the radius of a circumscribing sphere about a cube of edge length φ, and r_i is the apothem of a regular pentagon of edge length φ.

Area and volume

The surface area A and the volume V of a regular dodecahedron of edge length a are:

$A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.645728807a^{2}$

$V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.6631189606a^{3}$

Two dimensional symmetry projections

The dodecahedron has two special orthogonal projections, centered, on vertices and pentagonal faces, correspond to the A₂ and H₂ Coxeter planes.

Orthogonal projections

Centered by	Vertex	Edge	Face
Image
Projective symmetry	[[3]] = [6]	[2]	[[5]] = [10]

In perspective projection, viewed above a pentagonal face, the dodecahedron can be seen as a linear-edged schlegel diagram, or stereographic projection as a spherical polyhedron. These projections are also used in showing the four dimensional 120-cell, a regular 4-dimensional polytope, constructed from 120 dodecahedra, projecting it down to 3-dimensions.

Perspective projections

Polyhedron	Spherical

Cartesian coordinates

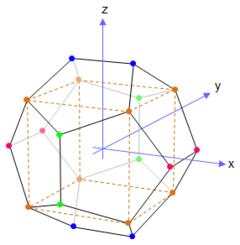
Vertex coordinates:
	The orange vertices lie at (±1, ±1, ±1) and form a cube (dotted lines).
	The green vertices lie at (0, ±1/φ, ±φ) and form a rectangle on the y–z plane.
	The blue vertices lie at (±1/φ, ±φ, 0) and form a rectangle on the x–y plane.
	The pink vertices lie at (±φ, 0, ±1/φ) and form a rectangle on the x–z plane.
The distance between adjacent vertices is 2/φ, and the distance from the origin to any vertex is √3. φ = (1 + √5) / 2 is the golden ratio.

The following Cartesian coordinates define the vertices of a dodecahedron centered at the origin and suitably scaled and oriented:

(±1, ±1, ±1)

(0, ±1/φ, ±φ)

(±1/φ, ±φ, 0)

(±φ, 0, ±1/φ)

where φ = (1 + √5) / 2 is the golden ratio (also written τ) ≈ 1.618. The edge length is 2/φ = √5 – 1. The containing sphere has a radius of √3.

Properties

• The dihedral angle of a dodecahedron is 2 arctan(φ) or approximately 116.5650512 degrees (where again φ = (1 + √5) / 2, the golden ratio). OEIS: A137218
• If the original dodecahedron has edge length 1, its dual icosahedron has edge length φ.
• If the five Platonic solids are built with same volume, the dodecahedron has the shortest edges.
• It has 43,380 nets.
• The map-coloring number of a regular dodecahedron's faces is 4.
• The distance between the vertices on the same face not connected by an edge is φ times the edge length,

Geometric relations

The regular dodecahedron is the third in an infinite set of truncated trapezohedra which can be constructed by truncating the two axial vertices of a pentagonal trapezohedron.

The stellations of the dodecahedron make up three of the four Kepler-Poinsot polyhedra.

A rectified dodecahedron forms an icosidodecahedron.

The regular dodecahedron has 120 symmetries, forming the group A₅ × Z₂.

Icosahedron vs dodecahedron

When a dodecahedron is inscribed in a sphere, it occupies more of the sphere's volume (66.49%) than an icosahedron inscribed in the same sphere (60.54%).

A regular dodecahedron with edge length 1 has more than three and a half times the volume of an icosahedron with the same length edges (7.663... compared with 2.181...).

A regular dodecahedron has 12 faces and 20 vertices, whereas a regular icosahedron has 20 faces and 12 vertices. Both have 30 edges.

Related polyhedra and tilings

The regular dodecahedron is topologically related to a series of tilings by vertex figure n³.

*n32 symmetry mutation of regular tilings: {n,3}
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

The dodecahedron can be transformed by a truncation sequence into its dual, the icosahedron:

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

The regular dodecahedron is a member of a sequence of otherwise non-uniform polyhedra and tilings, composed of pentagons with face configurations (V3.3.3.3.n). (For n > 6, the sequence consists of tilings of the hyperbolic plane.) These face-transitive figures have (n32) rotational symmetry.

n32 symmetry mutations of snub tilings: 3.3.3.3.n
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Vertex arrangement

The dodecahedron shares its vertex arrangement with four nonconvex uniform polyhedra and three uniform polyhedron compounds.

Five cubes fit within, with their edges as diagonals of the dodecahedron's faces, and together these make up the regular polyhedral compound of five cubes. Since two tetrahedra can fit on alternate cube vertices, five and ten tetrahedra can also fit in a dodecahedron.

Great stellated dodecahedron	Small ditrigonal icosidodecahedron	Ditrigonal dodecadodecahedron	Great ditrigonal icosidodecahedron
Compound of five cubes	Compound of five tetrahedra	Compound of ten tetrahedra

Stellations

The 3 stellations of the dodecahedron are all regular (nonconvex) polyhedra: (Kepler–Poinsot polyhedra)

	0	1	2	3
Stellation	Dodecahedron	Small stellated dodecahedron	Great dodecahedron	Great stellated dodecahedron
Facet diagram

Other dodecahedra

Topologically identical irregular dodecahedra

The truncated pentagonal trapezohedron has D5d dihedral symmetry.

The pyritohedron has Th tetrahedral symmetry.

The term dodecahedron is also used for other polyhedra with twelve faces, most notably the rhombic dodecahedron which is dual to the cuboctahedron (an Archimedean solid) and occurs in nature as a crystal form. The Platonic solid dodecahedron can be called a pentagonal dodecahedron or a regular dodecahedron to distinguish it. The pyritohedron is an irregular pentagonal dodecahedron.

Topologically distinct dodecahedra include:

• Pentagonal dodecahedra:
  • Regular dodecahedron, 12 pentagonal faces, I_h symmetry, order 120
  • Pentagonal truncated trapezohedron - same topology as regular form, but D_5d symmetry, order 20
  • "Pyritohedron" - same topology as regular form, but T_h symmetry, order 12
• Uniform polyhedra:
  • Decagonal prism – 10 squares, 2 decagons, D_10h symmetry, order 40
  • Pentagonal antiprism – 10 equilateral triangles, 2 pentagons, D_5d symmetry, order 20
• Johnson solids (regular faced):
  • Pentagonal cupola – 5 triangles, 5 squares, 1 pentagon, 1 decagon, C_5v symmetry, order 10
  • Snub disphenoid – 12 triangles, D_2d, order 8
  • Elongated square dipyramid – 8 triangles and 4 squares, D_4h symmetry, order 16
  • Metabidiminished icosahedron – 10 triangles and 2 pentagons, C_2v symmetry, order 4
• Congruent nonregular faced: (face-transitive)
  • Hexagonal bipyramid – 12 isosceles triangles, dual of hexagonal prism, D_6h symmetry, order 24
  • Hexagonal trapezohedron – 12 kites, dual of hexagonal antiprism, D_6d symmetry, order 24
  • Triakis tetrahedron – 12 isosceles triangles, dual of truncated tetrahedron, T_d symmetry, order 24
  • Rhombic dodecahedron (mentioned above) – 12 rhombi, dual of cuboctahedron, O_h symmetry, order 48
• Other nonregular faced:
  • Hendecagonal pyramid – 11 isosceles triangles and 1 hendecagon, C_11v, order 11
  • Trapezo-rhombic dodecahedron – 6 rhombi, 6 trapezoids – dual of triangular orthobicupola, D_3h symmetry, order 12
  • Rhombo-hexagonal dodecahedron or Elongated Dodecahedron – 8 rhombi and 4 equilateral hexagons, D_4h symmetry, order 16

In all there are 6,384,634 topologically distinct dodecahedra.

History and uses

Roman dodecahedron

Ho-Mg-Zn quasicrystal

Omnidirectional sound source

A climbing wall consisting of three dodecahedral pieces

Dodecahedral objects have found some practical applications, and have also played a role in the visual arts and in philosophy.

Plato's dialogue Timaeus (c. 360 B.C.) associates the other four platonic solids with the four classical elements, adding that "there is a fifth figure (which is made out of twelve pentagons), the dodecahedron—this God used as a model for the twelvefold division of the Zodiac." Aristotle postulated that the heavens were made of a fifth element, aithêr (aether in Latin, ether in American English), but he had no interest in matching it with Plato's fifth solid.

A few centuries later, small, hollow bronze Roman dodecahedra were made and have been found in various Roman ruins in Europe. Their purpose is not certain.

In 20th-century art, dodecahedra appear in the work of M.C. Escher, such as his lithograph Reptiles (1943), and in his Gravitation. In Salvador Dalí's painting The Sacrament of the Last Supper (1955), the room is a hollow dodecahedron.

In modern role-playing games, the dodecahedron is often used as a twelve-sided die, one of the more common polyhedral dice. Some quasicrystals have dodecahedral shape (see figure). Some regular crystals such as garnet and diamond are also said to exhibit "dodecahedral" habit, but this statement actually refers to the rhombic dodecahedron shape.

Immersive media, a Camera manufacturing company, has made the Dodeca 2360 camera, the world's first 360°, full motion camera which captures high-resolution video from every direction simultaneously at more than 100 million pixels per second or 30 frames per second. It is based on dodecahedron.

The popular puzzle game Megaminx is in the shape of a dodecahedron.

In the children's novel The Phantom Tollbooth, the Dodecahedron appears as a character in the land of Mathematics. Each of his faces wears a different expression—e.g. happy, angry, sad—which he swivels to the front as required to match his mood.

Dodecahedron is the name of avant-garde black metal band from Netherlands.

Shape of the universe

Various models have been proposed for the global geometry of the universe. In addition to the primitive geometries, these proposals include the Poincaré dodecahedral space, a positively curved space consisting of a dodecahedron whose opposite faces correspond (with a small twist). This was proposed by Jean-Pierre Luminet and colleagues in 2003 and an optimal orientation on the sky for the model was estimated in 2008.

In Bertrand Russell's 1954 short story "THE MATHEMATICIAN'S NIGHTMARE: The Vision of Professor Squarepunt," the number 5 said: "I am the number of fingers on a hand. I make pentagons and pentagrams. And but for me dodecahedra could not exist; and, as everyone knows, the universe is a dodecahedron. So, but for me, there could be no universe."

As a graph

A Hamiltonian cycle in a dodecahedron.

The skeleton of the dodecahedron—the vertices and edges—form a graph. This graph can also be constructed as the generalized Petersen graph G(10, 2). The high degree of symmetry of the polygon is replicated in the properties of this graph, which is distance-transitive, distance-regular, and symmetric. The automorphism group has order 120. The vertices can be colored with 3 colors, as can the edges, and the diameter is 5.

The dodecahedral graph is Hamiltonian—there is a cycle containing all the vertices. Indeed, this name derives from a mathematical game invented in 1857 by William Rowan Hamilton, the icosian game. The game's object was to find a Hamiltonian cycle along the edges of a dodecahedron.

See also

• Truncated dodecahedron
• Snub dodecahedron
• Pentakis dodecahedron
• 120-cell: a regular polychoron (4D polytope) whose surface consists of 120 dodecahedral cells.

External links

• Weisstein, Eric W. "Dodecahedron". MathWorld.
• Weisstein, Eric W. "Elongated Dodecahedron". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra o3o5x – doe".
• Editable printable net of a dodecahedron with interactive 3D view
• The Uniform Polyhedra
• Origami Polyhedra – Models made with Modular Origami
• Dodecahedron – 3-d model that works in your browser
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models
  1. Regular dodecahedron regular
  2. Rhombic dodecahedron quasiregular
  3. Decagonal prism vertex-transitive
  4. Pentagonal antiprism vertex-transitive
  5. Hexagonal dipyramid face-transitive
  6. Triakis tetrahedron face-transitive
  7. hexagonal trapezohedron face-transitive
  8. Pentagonal cupola regular faces
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Dodecahedron 3D Visualization
• Stella: Polyhedron Navigator: Software used to create some of the images on this page.