List of numeral systems
| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
There are many different numeral systems, that is, writing systems for expressing numbers.
By culture / time period
[edit]"A base is a natural number B whose powers (B multiplied by itself some number of times) are specially designated within a numerical system."[1]: 38 The term is not equivalent to radix, as it applies to all numerical notation systems (not just positional ones with a radix) and most systems of spoken numbers.[1] Some systems have two bases, a smaller (subbase) and a larger (base); an example is Roman numerals, which are organized by fives (V=5, L=50, D=500, the subbase) and tens (X=10, C=100, M=1,000, the base).
| Name | Base | Sample | Approx. First Appearance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Proto-cuneiform numerals | 10&60 | c. 3500–2000 BCE | ||||||||||
| Indus numerals | c. 3500–1900 BCE | |||||||||||
| Proto-Elamite numerals | 10&60 | 3100 BCE | ||||||||||
| Sumerian numerals | 10&60 | 3100 BCE | ||||||||||
| Egyptian numerals | 10 |
|
3000 BCE | |||||||||
| Babylonian numerals | 10&60 | 2000 BCE | ||||||||||
| Aegean numerals | 10 | 𐄇 𐄈 𐄉 𐄊 𐄋 𐄌 𐄍 𐄎 𐄏 ( 𐄐 𐄑 𐄒 𐄓 𐄔 𐄕 𐄖 𐄗 𐄘 ( 𐄙 𐄚 𐄛 𐄜 𐄝 𐄞 𐄟 𐄠 𐄡 ( 𐄢 𐄣 𐄤 𐄥 𐄦 𐄧 𐄨 𐄩 𐄪 ( 𐄫 𐄬 𐄭 𐄮 𐄯 𐄰 𐄱 𐄲 𐄳 ( |
1500 BCE | |||||||||
| Chinese numerals Japanese numerals Korean numerals (Sino-Korean) Vietnamese numerals (Sino-Vietnamese) |
10 |
零一二三四五六七八九十百千萬億 (Default, Traditional Chinese) |
1300 BCE | |||||||||
| Roman numerals | 5&10 | I V X L C D M | 1000 BCE[1] | |||||||||
| Hebrew numerals | 10 | א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ ק ר ש ת ך ם ן ף ץ |
800 BCE | |||||||||
| Indian numerals | 10 |
Bengali ০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯ Devanagari ० १ २ ३ ४ ५ ६ ७ ८ ९ Gujarati ૦ ૧ ૨ ૩ ૪ ૫ ૬ ૭ ૮ ૯ Kannada ೦ ೧ ೨ ೩ ೪ ೫ ೬ ೭ ೮ ೯ Malayalam ൦ ൧ ൨ ൩ ൪ ൫ ൬ ൭ ൮ ൯ Odia ୦ ୧ ୨ ୩ ୪ ୫ ୬ ୭ ୮ ୯ Punjabi ੦ ੧ ੨ ੩ ੪ ੫ ੬ ੭ ੮ ੯ Tamil ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ Telugu ౦ ౧ ౨ ౩ ౪ ౫ ౬ ౭ ౮ ౯ Tibetan ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ Urdu ۰ ۱ ۲ ۳ ۴ ۵ ۶ ۷ ۸ ۹ |
750–500 BCE | |||||||||
| Greek numerals | 10 | ō α β γ δ ε ϝ ζ η θ ι ο Αʹ Βʹ Γʹ Δʹ Εʹ Ϛʹ Ζʹ Ηʹ Θʹ |
<400 BCE | |||||||||
| Kharosthi numerals | 4&10 | 𐩇 𐩆 𐩅 𐩄 𐩃 𐩂 𐩁 𐩀 | <400–250 BCE[2] | |||||||||
| Phoenician numerals | 10 | 𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖 [3] | <250 BCE[4] | |||||||||
| Chinese rod numerals | 10 | 𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩 | 1st Century | |||||||||
| Coptic numerals | 10 | Ⲁ Ⲃ Ⲅ Ⲇ Ⲉ Ⲋ Ⲍ Ⲏ Ⲑ | 2nd Century | |||||||||
| Ge'ez numerals | 10 | ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ ፻ ፼ [5] |
3rd–4th Century 15th Century (Modern Style)[6] | |||||||||
| Armenian numerals | 10 | Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ | Early 5th Century | |||||||||
| Khmer numerals | 10 | ០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩ | Early 7th Century | |||||||||
| Thai numerals | 10 | ๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙ | 7th Century[7] | |||||||||
| Abjad numerals | 10 | غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا | <8th Century | |||||||||
| Chinese numerals (financial) | 10 | 零壹貳參肆伍陸柒捌玖拾佰仟萬億 (T. Chinese) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (S. Chinese) |
late 7th/early 8th Century[8] | |||||||||
| Eastern Arabic numerals | 10 | ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١ ٠ | 8th Century | |||||||||
| Vietnamese numerals (Chữ Nôm) | 10 | 𠬠 𠄩 𠀧 𦊚 𠄼 𦒹 𦉱 𠔭 𠃩 | <9th Century | |||||||||
| Western Arabic numerals | 10 | 0 1 2 3 4 5 6 7 8 9 | 9th Century | |||||||||
| Glagolitic numerals | 10 | Ⰰ Ⰱ Ⰲ Ⰳ Ⰴ Ⰵ Ⰶ Ⰷ Ⰸ ... | 9th Century | |||||||||
| Cyrillic numerals | 10 | а в г д е ѕ з и ѳ і ... | 10th Century | |||||||||
| Rumi numerals | 10 | 10th Century | ||||||||||
| Burmese numerals | 10 | ၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉ | 11th Century[9] | |||||||||
| Tangut numerals | 10 | 𘈩 𗍫 𘕕 𗥃 𗏁 𗤁 𗒹 𘉋 𗢭 𗰗 | 11th Century (1036) | |||||||||
| Cistercian numerals | 10 | 13th Century | ||||||||||
| Maya numerals | 5&20 | <15th Century | ||||||||||
| Muisca numerals | 20 |  |
<15th Century | |||||||||
| Korean numerals (Hangul) | 10 | 영 일 이 삼 사 오 육 칠 팔 구 | 15th Century (1443) | |||||||||
| Aztec numerals | 20 | 16th Century | ||||||||||
| Sinhala numerals | 10 | ෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ 𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴 |
<18th Century | |||||||||
| Pentadic runes | 10 | 19th Century | ||||||||||
| Cherokee numerals | 10 | 19th Century (1820s) | ||||||||||
| Vai numerals | 10 | ꘠ ꘡ ꘢ ꘣ ꘤ ꘥ ꘦ ꘧ ꘨ ꘩ [10] | 19th Century (1832)[11] | |||||||||
| Bamum numerals | 10 | ꛯ ꛦ ꛧ ꛨ ꛩ ꛪ ꛫ ꛬ ꛭ ꛮ [12] | 19th Century (1896)[11] | |||||||||
| Mende Kikakui numerals | 10 | 𞣏 𞣎 𞣍 𞣌 𞣋 𞣊 𞣉 𞣈 𞣇 [13] | 20th Century (1917)[14] | |||||||||
| Osmanya numerals | 10 | 𐒠 𐒡 𐒢 𐒣 𐒤 𐒥 𐒦 𐒧 𐒨 𐒩 | 20th Century (1920s) | |||||||||
| Medefaidrin numerals | 20 | 𖺀 𖺁/𖺔 𖺂/𖺕 𖺃/𖺖 𖺄 𖺅 𖺆 𖺇 𖺈 𖺉 𖺊 𖺋 𖺌 𖺍 𖺎 𖺏 𖺐 𖺑 𖺒 𖺓 [15] | 20th Century (1930s)[16] | |||||||||
| N'Ko numerals | 10 | ߉ ߈ ߇ ߆ ߅ ߄ ߃ ߂ ߁ ߀ [17] | 20th Century (1949)[18] | |||||||||
| Hmong numerals | 10 | 𖭐 𖭑 𖭒 𖭓 𖭔 𖭕 𖭖 𖭗 𖭘 𖭑𖭐 | 20th Century (1959) | |||||||||
| Garay numerals | 10 |  [19] [19] |
20th Century (1961)[20] | |||||||||
| Adlam numerals | 10 | 𞥙 𞥘 𞥗 𞥖 𞥕 𞥔 𞥓 𞥒 𞥑 𞥐 [21] | 20th Century (1989)[22] | |||||||||
| Kaktovik numerals | 5&20 | 𝋀 𝋁 𝋂 𝋃 𝋄 𝋅 𝋆 𝋇 𝋈 𝋉 𝋊 𝋋 𝋌 𝋍 𝋎 𝋏 𝋐 𝋑 𝋒 𝋓 [23] |
20th Century (1994)[24] | |||||||||
| Sundanese numerals | 10 | ᮰ ᮱ ᮲ ᮳ ᮴ ᮵ ᮶ ᮷ ᮸ ᮹ | 20th Century (1996)[25] |
By type of notation
[edit]Numeral systems are classified here as to whether they use positional notation (also known as place-value notation), and further categorized by radix or base.
Standard positional numeral systems
[edit]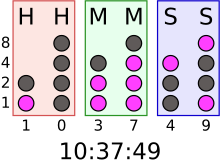
The common names are derived somewhat arbitrarily from a mix of Latin and Greek, in some cases including roots from both languages within a single name.[26] There have been some proposals for standardisation.[27]
| Base | Name | Usage |
|---|---|---|
| 2 | Binary | Digital computing, imperial and customary volume (bushel-kenning-peck-gallon-pottle-quart-pint-cup-gill-jack-fluid ounce-tablespoon) |
| 3 | Ternary | Cantor set (all points in [0,1] that can be represented in ternary with no 1s); counting Tasbih in Islam; hand-foot-yard and teaspoon-tablespoon-shot measurement systems; most economical integer base |
| 4 | Quaternary | Chumashan languages and Kharosthi numerals |
| 5 | Quinary | Gumatj, Ateso, Nunggubuyu, Kuurn Kopan Noot, and Saraveca languages; common count grouping e.g. tally marks |
| 6 | Senary, seximal | Diceware, Ndom, Kanum, and Proto-Uralic language (suspected) |
| 7 | Septimal, Septenary[28] | Weeks timekeeping, Western music letter notation |
| 8 | Octal | Charles XII of Sweden, Unix-like permissions, Squawk codes, DEC PDP-11, Yuki, Pame, compact notation for binary numbers, Xiantian (I Ching, China) |
| 9 | Nonary, nonal | Compact notation for ternary |
| 10 | Decimal, denary | Most widely used by contemporary societies[29][30][31] |
| 11 | Undecimal, unodecimal, undenary | A base-11 number system was attributed to the Māori (New Zealand) in the 19th century[32] and the Pangwa (Tanzania) in the 20th century.[33] Briefly proposed during the French Revolution to settle a dispute between those proposing a shift to duodecimal and those who were content with decimal. Used as a check digit in ISBN for 10-digit ISBNs. Applications in computer science and technology.[34][35][36] Featured in popular fiction. |
| 12 | Duodecimal, dozenal | Languages in the Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, and the Nimbia dialect of Gwandara; Chepang language of Nepal, and the Mahl dialect of Maldivian; dozen-gross-great gross counting; 12-hour clock and months timekeeping; years of Chinese zodiac; foot and inch; Roman fractions; penny and shilling |
| 13 | Tredecimal, tridecimal[37][38] | Conway base 13 function. |
| 14 | Quattuordecimal, quadrodecimal[37][38] | Programming for the HP 9100A/B calculator[39] and image processing applications;[40] pound and stone. |
| 15 | Quindecimal, pentadecimal[41][38] | Telephony routing over IP, and the Huli language. |
| 16 | Hexadecimal, sexadecimal, sedecimal | Compact notation for binary data; tonal system; ounce and pound. |
| 17 | Septendecimal, heptadecimal[41][38] | |
| 18 | Octodecimal[41][38] | A base in which 7n is palindromic for n = 3, 4, 6, 9. |
| 19 | Undevicesimal, nonadecimal[41][38] | |
| 20 | Vigesimal | Basque, Celtic, Muisca, Inuit, Yoruba, Tlingit, and Dzongkha numerals; Santali, and Ainu languages; shilling and pound |
| 5&20 | Quinary-vigesimal[42][43][44] | Greenlandic, Iñupiaq, Kaktovik, Maya, Nunivak Cupʼig, and Yupʼik numerals – "wide-spread... in the whole territory from Alaska along the Pacific Coast to the Orinoco and the Amazon"[42] |
| 21 | The smallest base in which all fractions 1/2 to 1/18 have periods of 4 or shorter. | |
| 23 | Kalam language,[45] Kobon language[citation needed] | |
| 24 | Quadravigesimal[46] | 24-hour clock timekeeping; Greek alphabet; Kaugel language. |
| 25 | Sometimes used as compact notation for quinary. | |
| 26 | Hexavigesimal[46][47] | Sometimes used for encryption or ciphering,[48] using all letters in the English alphabet |
| 27 | Septemvigesimal | Telefol,[45] Oksapmin,[49] Wambon,[50] and Hewa[51] languages. Mapping the nonzero digits to the alphabet and zero to the space is occasionally used to provide checksums for alphabetic data such as personal names,[52] to provide a concise encoding of alphabetic strings,[53] or as the basis for a form of gematria.[54] Compact notation for ternary. |
| 28 | Months timekeeping. | |
| 30 | Trigesimal | The Natural Area Code, this is the smallest base such that all of 1/2 to 1/6 terminate, a number n is a regular number if and only if 1/n terminates in base 30. |
| 32 | Duotrigesimal | Found in the Ngiti language. |
| 33 | Use of letters (except I, O, Q) with digits in vehicle registration plates of Hong Kong. | |
| 34 | Using all numbers and all letters except I and O; the smallest base where 1/2 terminates and all of 1/2 to 1/18 have periods of 4 or shorter. | |
| 35 | Covers the ten decimal digits and all letters of the English alphabet, apart from not distinguishing 0 from O. | |
| 36 | Hexatrigesimal[55][56] | Covers the ten decimal digits and all letters of the English alphabet. |
| 37 | Covers the ten decimal digits and all letters of the Spanish alphabet. | |
| 38 | Covers the duodecimal digits and all letters of the English alphabet. | |
| 40 | Quadragesimal | DEC RADIX 50/MOD40 encoding used to compactly represent file names and other symbols on Digital Equipment Corporation computers. The character set is a subset of ASCII consisting of space, upper case letters, the punctuation marks "$", ".", and "%", and the numerals. |
| 42 | Largest base for which all minimal primes are known. | |
| 47 | Smallest base for which no generalized Wieferich primes are known. | |
| 49 | Compact notation for septenary. | |
| 50 | Quinquagesimal | SQUOZE encoding used to compactly represent file names and other symbols on some IBM computers. Encoding using all Gurmukhi characters plus the Gurmukhi digits. |
| 52 | Covers the digits and letters assigned to base 62 apart from the basic vowel letters;[57] similar to base 26 but distinguishing upper- and lower-case letters. | |
| 56 | A variant of base 58.[clarification needed][58] | |
| 57 | Covers base 62 apart from I, O, l, U, and u,[59] or I, 1, l, 0, and O.[60] | |
| 58 | Covers base 62 apart from 0 (zero), I (capital i), O (capital o) and l (lower case L).[61] | |
| 60 | Sexagesimal | Babylonian numerals and Sumerian; degrees-minutes-seconds and hours-minutes-seconds measurement systems; Ekari; covers base 62 apart from I, O, and l, but including _(underscore).[62] |
| 62 | Can be notated with the digits 0–9 and the cased letters A–Z and a–z of the English alphabet. | |
| 64 | Tetrasexagesimal | I Ching in China. This system is conveniently coded into ASCII by using the 26 letters of the Latin alphabet in both upper and lower case (52 total) plus 10 numerals (62 total) and then adding two special characters (+ and /). |
| 72 | The smallest base greater than binary such that no three-digit narcissistic number exists. | |
| 80 | Octogesimal | Used as a sub-base in Supyire. |
| 85 | Ascii85 encoding. This is the minimum number of characters needed to encode a 32 bit number into 5 printable characters in a process similar to MIME-64 encoding, since 855 is only slightly bigger than 232. Such method is 6.7% more efficient than MIME-64 which encodes a 24 bit number into 4 printable characters. | |
| 89 | Largest base for which all left-truncatable primes are known. | |
| 90 | Nonagesimal | Related to Goormaghtigh conjecture for the generalized repunit numbers (111 in base 90 = 1111111111111 in base 2). |
| 95 | Number of printable ASCII characters.[63] | |
| 96 | Total number of character codes in the (six) ASCII sticks containing printable characters. | |
| 97 | Smallest base which is not perfect odd power (where generalized Wagstaff numbers can be factored algebraically) for which no generalized Wagstaff primes are known. | |
| 100 | Centesimal | As 100=102, these are two decimal digits. |
| 121 | Number expressible with two undecimal digits. | |
| 125 | Number expressible with three quinary digits. | |
| 128 | Using as 128=27.[clarification needed] | |
| 144 | Number expressible with two duodecimal digits. | |
| 169 | Number expressible with two tridecimal digits. | |
| 185 | Smallest base which is not a perfect power (where generalized repunits can be factored algebraically) for which no generalized repunit primes are known. | |
| 196 | Number expressible with two tetradecimal digits. | |
| 210 | Smallest base such that all fractions 1/2 to 1/10 terminate. | |
| 225 | Number expressible with two pentadecimal digits. | |
| 256 | Number expressible with eight binary digits. | |
| 360 | Degrees of angle. |
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base‑1) | Tally marks, Counting |
| 10 | Bijective base-10 | To avoid zero |
| 26 | Bijective base-26 | Spreadsheet column numeration. Also used by John Nash as part of his obsession with numerology and the uncovering of "hidden" messages.[64] |
| Base | Name | Usage |
|---|---|---|
| 2 | Balanced binary (Non-adjacent form) | |
| 3 | Balanced ternary | Ternary computers |
| 4 | Balanced quaternary | |
| 5 | Balanced quinary | |
| 6 | Balanced senary | |
| 7 | Balanced septenary | |
| 8 | Balanced octal | |
| 9 | Balanced nonary | |
| 10 | Balanced decimal | John Colson Augustin Cauchy |
| 11 | Balanced undecimal | |
| 12 | Balanced duodecimal |
| Base | Name | Usage |
|---|---|---|
| 2i | Quater-imaginary base | related to base −4 and base 16 |
| Base | related to base −2 and base 4 | |
| Base | related to base 2 | |
| Base | related to base 8 | |
| Base | related to base 2 | |
| −1 ± i | Twindragon base | Twindragon fractal shape, related to base −4 and base 16 |
| 1 ± i | Negatwindragon base | related to base −4 and base 16 |
| Base | Name | Usage |
|---|---|---|
| Base | a rational non-integer base | |
| Base | related to duodecimal | |
| Base | related to decimal | |
| Base | related to base 2 | |
| Base | related to base 3 | |
| Base | ||
| Base | ||
| Base | usage in 12-tone equal temperament musical system | |
| Base | ||
| Base | a negative rational non-integer base | |
| Base | a negative non-integer base, related to base 2 | |
| Base | related to decimal | |
| Base | related to duodecimal | |
| φ | Golden ratio base | early Beta encoder[65] |
| ρ | Plastic number base | |
| ψ | Supergolden ratio base | |
| Silver ratio base | ||
| e | Base | best radix economy [citation needed] |
| π | Base | |
| eπ | Base | |
| Base |
| Base | Name | Usage |
|---|---|---|
| 2 | Dyadic number | |
| 3 | Triadic number | |
| 4 | Tetradic number | the same as dyadic number |
| 5 | Pentadic number | |
| 6 | Hexadic number | not a field |
| 7 | Heptadic number | |
| 8 | Octadic number | the same as dyadic number |
| 9 | Enneadic number | the same as triadic number |
| 10 | Decadic number | not a field |
| 11 | Hendecadic number | |
| 12 | Dodecadic number | not a field |
- Factorial number system {1, 2, 3, 4, 5, 6, ...}
- Even double factorial number system {2, 4, 6, 8, 10, 12, ...}
- Odd double factorial number system {1, 3, 5, 7, 9, 11, ...}
- Primorial number system {2, 3, 5, 7, 11, 13, ...}
- Fibonorial number system {1, 2, 3, 5, 8, 13, ...}
- {60, 60, 24, 7} in timekeeping
- {60, 60, 24, 30 (or 31 or 28 or 29), 12, 10, 10, 10} in timekeeping
- (12, 20) traditional English monetary system (£sd)
- (20, 18, 13) Maya timekeeping
Other
[edit]- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
- Combinatorial number system
Non-positional notation
[edit]All known numeral systems developed before the Babylonian numerals are non-positional,[66] as are many developed later, such as the Roman numerals. The French Cistercian monks created their own numeral system.
See also
[edit]- History of ancient numeral systems – Symbols representing numbers
- History of the Hindu–Arabic numeral system
- List of numeral system topics
- Numeral prefix – Prefix derived from numerals or other numbers
- Radix – Number of digits of a numeral system
- Radix economy – Number of digits needed to express a number in a particular base
- Table of bases – 0 to 1296 in base 2 to 36
- Timeline of numerals and arithmetic
References
[edit]- ^ a b c Chrisomalis, Stephen (2004). "A cognitive typology for numerical notation". Cambridge Archaeological Journal. 14 (1): 37–52. doi:10.1017/S0959774304000034.
- ^ https://www.unicode.org/L2/L2003/03314-kharoshthi.pdf [bare URL]
- ^ Everson, Michael (July 25, 2007). "Proposal to add two numbers for the Phoenician script" (PDF). UTC Document Register. Unicode Consortium. L2/07-206 (WG2 N3284).
- ^ Cajori, Florian (September 1928). A History Of Mathematical Notations Vol I. The Open Court Company. p. 18. Retrieved June 5, 2017.
- ^ "Ethiopic (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Chrisomalis, Stephen (January 18, 2010). Numerical Notation: A Comparative History. Cambridge University Press. pp. 135–136. ISBN 978-0-521-87818-0.
- ^ Chrisomalis 2010, p. 200.
- ^ Guo, Xianghe (July 27, 2009). "武则天为反贪发明汉语大写数字——中新网" [Wu Zetian invented Chinese capital numbers to fight corruption]. 中新社 [China News Service]. Retrieved August 15, 2024.
- ^ "Burmese/Myanmar script and pronunciation". Omniglot. Retrieved June 5, 2017.
- ^ "Vai (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ a b Kelly, Piers. "The invention, transmission and evolution of writing: Insights from the new scripts of West Africa". Open Science Framework.
- ^ "Bamum (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ "Mende Kikakui (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Everson, Michael (October 21, 2011). "Proposal for encoding the Mende script in the SMP of the UCS" (PDF). UTC Document Register. Unicode Consortium. L2/11-301R (WG2 N4133R).
- ^ "Medefaidrin (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Rovenchak, Andrij (July 17, 2015). "Preliminary proposal for encoding the Medefaidrin (Oberi Okaime) script in the SMP of the UCS (Revised)" (PDF). UTC Document Register. Unicode Consortium. L2/L2015.
- ^ "NKo (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Donaldson, Coleman (January 1, 2017). "Clear Language: Script, Register And The N'ko Movement Of Manding-Speaking West Africa" (PDF). repository.upenn.edu. UPenn.
- ^ "Consideration of the encoding of Garay with updated user feedback (revised)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Everson, Michael (March 22, 2016). "Proposal for encoding the Garay script in the SMP of the UCS" (PDF). UTC Document Register. Unicode Consortium. L2/L16-069 (WG2 N4709).
- ^ "Adlam (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Everson, Michael (October 28, 2014). "Revised proposal for encoding the Adlam script in the SMP of the UCS" (PDF). UTC Document Register. Unicode Consortium. L2/L14-219R (WG2 N4628R).
- ^ "Kaktovik Numerals (Unicode block)" (PDF). Unicode Character Code Charts. Unicode Consortium.
- ^ Silvia, Eduardo (February 9, 2020). "Exploratory proposal to encode the Kaktovik numerals" (PDF). UTC Document Register. Unicode Consortium. L2/20-070.
- ^ http://file.upi.edu/Direktori/FPBS/JUR._PEND._BHS._DAN_SASTRA_INDONESIA/197006242006041-TEDI_PERMADI/Direktori_Aksara_Sunda_untuk_Unicode.pdf [bare URL PDF]
- ^ For the mixed roots of the word "hexadecimal", see Epp, Susanna (2010), Discrete Mathematics with Applications (4th ed.), Cengage Learning, p. 91, ISBN 9781133168669.
- ^ Multiplication Tables of Various Bases, p. 45, Michael Thomas de Vlieger, Dozenal Society of America
- ^ "Definition of SEPTENARY". www.merriam-webster.com. Retrieved November 21, 2023.
- ^ The History of Arithmetic, Louis Charles Karpinski, 200pp, Rand McNally & Company, 1925.
- ^ Histoire universelle des chiffres, Georges Ifrah, Robert Laffont, 1994.
- ^ The Universal History of Numbers: From prehistory to the invention of the computer, Georges Ifrah, ISBN 0-471-39340-1, John Wiley and Sons Inc., New York, 2000. Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk
- ^ Overmann, Karenleigh A (2020). "The curious idea that Māori once counted by elevens, and the insights it still holds for cross-cultural numerical research". Journal of the Polynesian Society. 129 (1): 59–84. doi:10.15286/jps.129.1.59-84. Retrieved July 24, 2020.
- ^ Thomas, N.W (1920). "Duodecimal base of numeration". Man. 20 (1): 56–60. doi:10.2307/2840036. JSTOR 2840036. Retrieved July 25, 2020.
- ^ Ulrich, Werner (November 1957). "Non-binary error correction codes". Bell System Technical Journal. 36 (6): 1364–1365. doi:10.1002/j.1538-7305.1957.tb01514.x.
- ^ Das, Debasis; Lanjewar, U.A. (January 2012). "Realistic Approach of Strange Number System from Unodecimal to Vigesimal" (PDF). International Journal of Computer Science and Telecommunications. 3 (1). London: Sysbase Solution Ltd.: 13.
- ^ Rawat, Saurabh; Sah, Anushree (May 2013). "Subtraction in Traditional and Strange Number System by r's and r-1's Compliments". International Journal of Computer Applications. 70 (23): 13–17. Bibcode:2013IJCA...70w..13R. doi:10.5120/12206-7640.
... unodecimal, duodecimal, tridecimal, quadrodecimal, pentadecimal, heptadecimal, octodecimal, nona decimal, vigesimal and further are discussed...
- ^ a b Das & Lanjewar 2012, p. 13.
- ^ a b c d e f Rawat & Sah 2013.
- ^ HP 9100A/B programming, HP Museum
- ^ Free Patents Online
- ^ a b c d Das & Lanjewar 2012, p. 14.
- ^ a b Nykl, Alois Richard (September 1926). "The Quinary-Vigesimal System of Counting in Europe, Asia, and America". Language. 2 (3): 165–173. doi:10.2307/408742. JSTOR 408742. OCLC 50709582 – via Google Books. p. 165:
A student of the American Indian languages is naturally led to investigate the wide-spread use of the quinary-vigesimal system of counting which he meets in the whole territory from Alaska along the Pacific Coast to the Orinoco and the Amazon.
- ^ Eells, Walter Crosby (October 14, 2004). "Number Systems of the North American Indians". In Anderson, Marlow; Katz, Victor; Wilson, Robin (eds.). Sherlock Holmes in Babylon: And Other Tales of Mathematical History. Mathematical Association of America. p. 89. ISBN 978-0-88385-546-1 – via Google Books.
Quinary-vigesimal. This is most frequent. The Greenland Eskimo says 'other hand two' for 7, 'first foot two' for 12, 'other foot two' for 17, and similar combinations to 20, 'man ended.' The Unalit is also quinary to twenty, which is 'man completed.' ...
- ^ Chrisomalis 2010, p. 200: "The early origin of bar-and-dot numeration alongside the Middle Formative Mesoamerican scripts, the quinary-vigesimal structure of the system, and the general increase in the frequency and complexity of numeral expressions over time all point to its indigenous development.".
- ^ a b Laycock, Donald (1975). "Observations on Number Systems and Semantics". In Wurm, Stephen (ed.). New Guinea Area Languages and Language Study, I: Papuan Languages and the New Guinea Linguistic Scene. Pacific Linguistics C-38. Canberra: Research School of Pacific Studies, Australian National University. pp. 219–233.
- ^ a b Dibbell, Julian (2010). "Introduction". The Best Technology Writing 2010. Yale University Press. p. 9. ISBN 978-0-300-16565-4.
There's even a hexavigesimal digital code—our own twenty-six symbol variant of the ancient Latin alphabet, which the Romans derived in turn from the quadravigesimal version used by the ancient Greeks.
- ^ Young, Brian; Faris, Tom; Armogida, Luigi (2019). "A nomenclature for sequence-based forensic DNA analysis". Genetics. 42. Forensic Science International: 14–20. doi:10.1016/j.fsigen.2019.06.001. PMID 31207427.
[…] 2) the hexadecimal output of the hash function is converted to hexavigesimal (base-26); 3) letters in the hexavigesimal number are capitalized, while all numerals are left unchanged; 4) the order of the characters is reversed so that the hexavigesimal digits appear […]
- ^ "Base 26 Cipher (Number ⬌ Words) - Online Decoder, Encoder".
- ^ Saxe, Geoffrey B.; Moylan, Thomas (1982). "The development of measurement operations among the Oksapmin of Papua New Guinea". Child Development. 53 (5): 1242–1248. doi:10.1111/j.1467-8624.1982.tb04161.x. JSTOR 1129012..
- ^ "Безымянный палец • Задачи".
- ^ Nauka i Zhizn, 1992, issue 3, p. 48.
- ^ Grannis, Shaun J.; Overhage, J. Marc; McDonald, Clement J. (2002), "Analysis of identifier performance using a deterministic linkage algorithm", Proceedings. AMIA Symposium: 305–309, PMC 2244404, PMID 12463836.
- ^ Stephens, Kenneth Rod (1996), Visual Basic Algorithms: A Developer's Sourcebook of Ready-to-run Code, Wiley, p. 215, ISBN 9780471134183.
- ^ Sallows, Lee (1993), "Base 27: the key to a new gematria", Word Ways, 26 (2): 67–77.
- ^ Gódor, Balázs (2006). "World-wide user identification in seven characters with unique number mapping". Networks 2006: 12th International Telecommunications Network Strategy and Planning Symposium. IEEE. pp. 1–5. doi:10.1109/NETWKS.2006.300409. ISBN 1-4244-0952-7. S2CID 46702639.
This article proposes the Unique Number Mapping as an identification scheme, that could replace the E.164 numbers, could be used both with PSTN and VoIP terminals and makes use of the elements of the ENUM technology and the hexatrigesimal number system. […] To have the shortest IDs, we should use the greatest possible number system, which is the hexatrigesimal. Here the place values correspond to powers of 36...
- ^ Balagadde, Robert Ssali; Premchand, Parvataneni (2016). "The Structured Compact Tag-Set for Luganda". International Journal on Natural Language Computing (IJNLC). 5 (4).
Concord Numbers used in the categorisation of Luganda words encoded using either Hexatrigesimal or Duotrigesimal, standard positional numbering systems. […] We propose Hexatrigesimal system to capture numeric information exceeding 10 for adaptation purposes for other Bantu languages or other agglutinative languages.
- ^ "Base52". GitHub. Retrieved January 3, 2016.
- ^ "Base56". Retrieved January 3, 2016.
- ^ "Base57". GitHub. Retrieved January 3, 2016.
- ^ "Base57". GitHub. Retrieved January 22, 2019.
- ^ "The Base58 Encoding Scheme". Internet Engineering Task Force. November 27, 2019. Archived from the original on August 12, 2020. Retrieved August 12, 2020.
Thanks to Satoshi Nakamoto for inventing the Base58 encoding format
- ^ "NewBase60". Retrieved January 3, 2016.
- ^ "base95 Numeric System". Archived from the original on February 7, 2016. Retrieved January 3, 2016.
- ^ Nasar, Sylvia (2001). A Beautiful Mind. Simon and Schuster. pp. 333–6. ISBN 0-7432-2457-4.
- ^ Ward, Rachel (2008), "On Robustness Properties of Beta Encoders and Golden Ratio Encoders", IEEE Transactions on Information Theory, 54 (9): 4324–4334, arXiv:0806.1083, Bibcode:2008arXiv0806.1083W, doi:10.1109/TIT.2008.928235, S2CID 12926540
- ^ Chrisomalis 2010, p. 254: Chrisomalis calls the Babylonian system "the first positional system ever".



![{\displaystyle i{\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f48aaefa3cb6be4af4b2c08230fe6dfbc46ca34)

![{\displaystyle \omega {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef8760a51aec3a8be3be7ac8e05719a1a7a06efa)





![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
![{\displaystyle {\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa163183b2c3828db27e22253d454a643a4c936)
![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)









