Prime number

"Prime" redirects here. For other uses, see Prime (disambiguation).

Demonstration, with Cuisenaire rods, that the number 7 is prime, being divisible only by 1 and 7

A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because 1 and 5 are its only positive integer divisors, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily many instances of 1 in any factorization, e.g., 3, 1 · 3, 1 · 1 · 3, etc. are all valid factorizations of 3.

The property of being prime is called primality. A simple but slow method of verifying the primality of a given number n is known as trial division. It consists of testing whether n is a multiple of any integer between 2 and √n. Algorithms much more efficient than trial division have been devised to test the primality of large numbers. These include the Miller–Rabin primality test, which is fast but has a small probability of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of January 2018, the largest known prime number has 23,249,425 decimal digits.

There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known simple formula that separates prime numbers from composite numbers. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n.

Many questions regarding prime numbers remain open, such as Goldbach's conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals.

Definition and examples

Main article: List of prime numbers

A natural number (i.e. 1, 2, 3, 4, 5, 6, etc.) is called a prime number (or a prime) if it has exactly two positive divisors, 1 and the number itself. Natural numbers greater than 1 that are not prime are called composite.

Among other ways, 12 items can be placed into 3 equal-size columns of 4 each, meaning 3 and 4 are divisors of 12. Therefore, the number 12 is not a prime. There is no way to place 11 items into several equal-size columns of more than 1 item each without some extra items leftover (a remainder). Therefore, the number 11 is a prime.

For example, among the numbers 1 through 6, the numbers 2, 3, and 5 are the prime numbers, as there are no other numbers that divide them evenly. 1 is not a prime number because it has only one divisor, itself. 4 has three divisors: 1, 2, and 4. And 6 has four divisors: 1, 2, 3, and 6. So none of 1, 4, or 6 are prime. 4 and 6 are both composite.

The first 168 prime numbers (all the prime numbers less than 1000) are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997 (sequence A000040 in the OEIS).

No even number greater than 2 is prime because each has at least three divisors: 1, 2, and itself. Therefore, the prime numbers other than two are all odd numbers. They are often called odd primes. Similarly, when written in the usual decimal system, all prime numbers larger than 5 must end in 1, 3, 7, or 9. The numbers that end with other digits are all composite: decimal numbers that end in 0, 2, 4, 6, or 8 are even, and decimal numbers that end in 0 or 5 are divisible by 5.

Every natural number has both 1 and itself as a divisor. Therefore, if it has any other divisor, it cannot be prime. Based on this idea, the primes can be defined as the numbers without other divisors: a number n is prime if it is greater than one and if none of the numbers 2, 3, ..., n − 1 divides n evenly (without remainder). Yet another way to say the same thing is that a number n > 1 is prime if it cannot be written as a product of a × b of two integers a and b, both of which are larger than 1. In other words, n is prime if n items cannot be divided up into smaller equal-size groups of more than one item, or if it is not possible to arrange n dots into a rectangular grid that is more than one dot wide and more than one dot high.

The set of all primes is often denoted by P (a boldface capital P) or by $\mathbb {P}$ (a blackboard bold capital P).

Unique factorization and the primality of one

Fundamental theorem of arithmetic

Main article: Fundamental theorem of arithmetic

The crucial importance of prime numbers to number theory and mathematics in general stems from the fundamental theorem of arithmetic, which states that every integer larger than 1 can be written as a product of one or more primes in a way that is unique except for the order of the prime factors. Primes can thus be considered the "basic building blocks" of the natural numbers. For example:

23244	= 2 · 2 · 3 · 13 · 149
	= 22 · 3 · 13 · 149. (22 denotes the square or second power of 2.)

As in this example, the same prime factor may occur multiple times. A decomposition:

n = p₁ · p₂ · ... · p_t

of a number n into (finitely many) prime factors p₁, p₂, ... to p_t is called prime factorization of n. The fundamental theorem of arithmetic can be rephrased so as to say that any two factorizations of the same number into primes will be identical except for the order of the factors. So, although there are many different ways of finding a factorization using an integer factorization algorithm, they all must produce the same result.

If p is a prime number and p divides a product ab of integers, then p divides a or p divides b. This proposition is known as Euclid's lemma. It is used in some proofs of the uniqueness of prime factorizations.

Primality of one

Most early Greeks did not even consider 1 to be a number, so they could not consider it to be a prime. A few mathematicians from this time also considered the prime and composite numbers to be subdivisions of the odd numbers, so they also did not consider 2 to be prime. However, Plato, Aristotle, Euclid, and a majority of the other Greek mathematicians considered 2 as prime. The medieval Islamic mathematicians largely followed the Greeks in viewing 1 as not being a number.

By the Middle Ages and Renaissance mathematicians began treating 1 as a number, and some of them included it as the first prime number. In the mid-18th century Christian Goldbach listed 1 as the first prime in his famous correspondence with Leonhard Euler; however, Euler himself did not consider 1 to be a prime number. In the 19th century many mathematicians still considered the number 1 to be a prime. For example, Derrick Norman Lehmer's list of primes up to 10,006,721, reprinted as late as 1956, started with 1 as its first prime. Henri Lebesgue has been said to be the last professional mathematician to call 1 prime, but G. H. Hardy did so even later. By the early 20th century, mathematicians began to arrive at the consensus that 1 is not a prime number, but rather forms its own special category as a "unit".

If the definition of a prime number were changed to call 1 a prime, many statements involving the prime numbers would not hold in the form they are usually stated, but would instead require special treatment for the number 1. For example, the number 15 can be factored as 3 · 5 and 1 · 3 · 5, so if 1 were defined to be prime, the number 15 would have two different factorizations into prime numbers. In order for the fundamental theorem of arithmetic to remain valid with this definition, it would need to be rephrased in terms of factorizations into primes greater than 1. Similarly, the sieve of Eratosthenes would not work correctly if it handled 1 as a prime, because it would eliminate all multiples of 1 (that is, all other numbers) and produce as output only the single number 1. Some other more technical properties of prime numbers also do not hold for the number 1: for instance, the formulas for Euler's totient function or for the sum of divisors function are different for prime numbers than they are for 1.

History

The sieve of Eratosthenes is a simple algorithm for finding all prime numbers up to a specified integer. It was created in the 3rd century BC by Eratosthenes, an ancient Greek mathematician.

There are hints in the surviving records of the ancient Egyptians that they had some knowledge of prime numbers: the Egyptian fraction expansions in the Rhind papyrus, for instance, have quite different forms for primes and for composites. It has also been suggested that the Ishango bone records a list of prime numbers. However, the earliest surviving records of the explicit study of prime numbers come from Ancient Greek mathematics. Euclid's Elements (circa 300 BC) contain important theorems about primes, including the infinitude of primes and the fundamental theorem of arithmetic. Euclid also showed how to construct a perfect number from a Mersenne prime. The Sieve of Eratosthenes, attributed to Eratosthenes, is a simple method to compute primes, although the large primes found today with computers are not generated this way.

Wilson's theorem, characterizing the prime numbers as the solutions to the equation (n - 1)! ≡ -1 (mod n), was found around 1000 AD by an Islamic mathematician, Ibn al-Haytham (Alhazen). Ibn al-Haytham also investigated the perfect numbers formed from Mersenne primes, and conjectured that all perfect numbers arose in this way, but was unable to prove it. Another Islamic mathematician, Ibn al-Banna' al-Marrakushi, observed that the sieve of Eratosthenes can be sped up by testing only the divisors up to the square root of the largest number to be tested. Fibonacci brought Islamic mathematics back to Europe. His book Liber Abaci (1202) was the first to describe trial division for testing primality, again using divisors only up to the square root.

The next significant developments took place in 17th and 18th century Europe. In 1640 Pierre de Fermat stated (without proof) Fermat's little theorem (later proved by Leibniz and Euler). Fermat also conjectured that all numbers of the form 2²ⁿ + 1 are prime (they are called Fermat numbers) and he verified this up to n = 4 (or 2¹⁶ + 1). However, the very next Fermat number 2³² + 1 is composite (one of its prime factors is 641), as Euler discovered later, and in fact no further Fermat numbers are known to be prime. The French monk Marin Mersenne looked at primes of the form 2^p - 1, with p a prime. They are called Mersenne primes in his honor. Christian Goldbach formulated Goldbach's conjecture, that every even number is the sum of two primes, in a 1742 letter to Euler. Euler's work in number theory included many results about primes. He showed the infinite series 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + … is divergent. In 1747 he proved Ibn al-Haytham's conjecture (now the Euclid–Euler theorem) that the even perfect numbers are precisely the integers of the form 2^p−1(2^p − 1), where the second factor is a Mersenne prime.

At the start of the 19th century, Legendre and Gauss independently conjectured that as x tends to infinity, the number of primes up to x is asymptotic to x/ln x, where ln x is the natural logarithm of x. Ideas of Riemann in his 1859 paper on the zeta-function sketched an outline for proving this. Although the closely related Riemann hypothesis remains unproven, Riemann's outline was completed in 1896 by Hadamard and de la Vallée Poussin, independently of each other, and the result is now known as the prime number theorem. Another important 19th-century result was Dirichlet's theorem on arithmetic progressions, that every arithmetic progression contains infinitely many primes.

Many mathematicians have worked on primality tests for larger numbers than would be possible by trial division. Some of these methods are restricted to specific number forms; this includes Pépin's test for Fermat numbers (1877), Proth's theorem (around 1878), the Lucas–Lehmer primality test (originated 1856), and the generalized Lucas primality test. More recent algorithms like the Adleman–Pomerance–Rumely primality test, Elliptic curve primality proving, and the AKS primality test work on arbitrary numbers but are slower than the algorithms for specific number forms. Since 1951 all the largest known primes have been found by computers. The search for ever larger primes has generated interest outside mathematical circles. The Great Internet Mersenne Prime Search and other distributed computing projects to find large primes have become popular, while mathematicians continue to struggle with the theory of primes.

For a long time, prime numbers were thought to have extremely limited application outside of pure mathematics. This changed in the 1970s when the concepts of public-key cryptography were invented, in which prime numbers formed the basis of the first algorithms such as the RSA cryptosystem algorithm. Important recent developments in the theory of prime numbers include the Green–Tao theorem (2004) on long arithmetic progressions of prime numbers, and Yitang Zhang's 2013 proof that there exist infinitely many prime gaps of bounded size.

Number of prime numbers

Main article: Euclid's theorem

There are infinitely many prime numbers. Another way of saying this is that the sequence

2, 3, 5, 7, 11, 13, ...

of prime numbers never ends. This statement is referred to as Euclid's theorem in honor of the ancient Greek mathematician Euclid, since the first known proof for this statement is attributed to him. Many more proofs of the infinitude of primes are known, including an analytical proof by Euler, Goldbach's proof based on Fermat numbers, Furstenberg's proof using general topology, and Kummer's elegant proof.

Euclid's proof

Euclid's proof that there are infinitely many primes (Book IX, Proposition 20) shows equivalently that every finite set S of primes misses at least one prime. The key idea is to multiply together the numbers in S and add one:

$N=1+\prod _{p\in S}p.$

Because the resulting number N is greater than one, it has at least one prime number (possibly N itself) in its prime factorization. But this prime cannot be in S, because dividing N by any one of the primes in S leaves a remainder of 1. Therefore, S does not contain all the primes.

It is often erroneously reported that Euclid begins with the assumption that the set S contains all prime numbers, leading to a contradiction, or that S contains all the primes up to some threshold rather than any arbitrary finite collection of primes. The numbers formed by adding one to the products of the smallest primes are called the Euclid numbers.

Euler's analytical proof

Euler's proof uses the partial sums of the reciprocals of primes,

$S(p)={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots +{\frac {1}{p}}.$

For any arbitrary real number x, there exists a prime p for which this partial sum is bigger than x. This shows that there are infinitely many primes, because if there were finitely many primes the sum would reach its maximum value at the biggest prime rather than being unbounded. More precisely, the growth rate of S(p) is doubly logarithmic, as quantified by Mertens' second theorem. For comparison, the sum

${\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}=\sum _{i=1}^{n}{\frac {1}{i^{2}}}$

does not grow to infinity as n goes to infinity (see Basel problem). In this sense, prime numbers occur more often than squares of natural numbers. Brun's theorem states that the sum of the reciprocals of twin primes,

$\left({{\frac {1}{3}}+{\frac {1}{5}}}\right)+\left({{\frac {1}{5}}+{\frac {1}{7}}}\right)+\left({{\frac {1}{11}}+{\frac {1}{13}}}\right)+\cdots =\sum \limits _{\begin{smallmatrix}p{\text{ prime, }}\\p+2{\text{ prime}}\end{smallmatrix}}{\left({{\frac {1}{p}}+{\frac {1}{p+2}}}\right)},$

is finite. Because of Brun's theorem, it is not possible to use Euler's method to solve the twin prime conjecture, that there exist infinitely many twin primes.

Testing primality and integer factorization

Main article: primality test

There are various methods to determine whether a given number n is prime. The most basic routine, trial division, is too slow to be useful for large numbers. One group of modern primality tests is applicable to arbitrary numbers, while more efficient tests are available for numbers of special types. Most primality tests only tell whether their argument is prime or not. Routines that also also provide a prime factor of composite arguments (or all of its prime factors) are called factorization algorithms.

Trial division

Main article: trial division

The most basic method of checking the primality of a given integer n is called trial division. This method divides n by each integer from 2 to the square root of n (inclusive). If any of these numbers divides n without a remainder, n is composite; otherwise it is prime. Factors larger than the square root do not need to be checked because, whenever n has a factor m bigger than the square root, it will also have another factor n/m smaller than the square root. Another optimization is to check only prime divisors in this range. For instance, to check whether 37 is prime, this method divides it by the primes in the range from 2 to √37, which are 2, 3, and 5. Each division produces a nonzero remainder, so 37 is indeed prime.

Although this method is simple to describe, it is impractical for testing the primality of large integers because the number of divisions needed grows too rapidly. However, trial division is still used, with a smaller limit on the divisor size than the square root, to quickly filter out composite numbers with small factors before using more complicated methods on the numbers that pass this test.

Sieves

Main article: sieve of Eratosthenes

Before computers, mathematical tables listing all of the primes or prime factorizations up to a given limit were commonly printed. With them, one could determine whether a given number was prime by checking the table rather than doing any calculations. Although these are no longer used, it is still sometimes useful to generate lists of all small prime numbers. The oldest method for this is called the sieve of Eratosthenes; variants of this method are still commonly used. It operates by maintaining a table of Boolean values indicating whether each position in the table is divisible by any of the primes found so far. It loops through the table and, when it finds a position p that is not divisible by any earlier primes, outputs p as its next prime number. Then, it marks each multiple of p as being divisible by p. Another more efficient sieving method for the same problem is the sieve of Atkin. In advanced mathematics, sieve theory applies similar methods to other problems.

Primality testing versus primality proving

Some of the fastest modern tests for whether an arbitrary given number n is prime are probabilistic (or Monte Carlo) algorithms, meaning that they have a small random chance of producing an incorrect answer. For example, a given test might have the property that prime numbers will always pass the test, and that composite numbers will usually fail the test, but that a composite number could erroneously pass with some small probability p. A composite number that passes such a test is called a pseudoprime. If the test is repeated n times on the same number, the probability that a composite number could pass the test every time is pⁿ, which decreases exponentially with the number of tests, providing high confidence (although not certainty) that a number that passes the repeated test is prime. On the other hand, if the test ever fails, then the number is certainly composite. Probabilistic tests with this behavior include the Solovay–Strassen primality test and the Miller–Rabin primality test.

In contrast, some other algorithms guarantee that their answer will always be correct: primes will always be determined to be prime and composites will always be determined to be composite. For instance, this is true of trial division. The algorithms with guaranteed-correct output include both deterministic (non-random) algorithms, such as the AKS primality test, and randomized Las Vegas algorithms where the random choices made by the algorithm do not affect its final answer, such as some variations of elliptic curve primality proving. The elliptic curve primality test is the fastest in practice of the guaranteed-correct primality tests, but its runtime analysis is based on heuristic arguments rather than rigorous proofs. The AKS primality test has mathematically proven time complexity, but is slower than elliptic curve primality proving in practice. When using these methods to generate large random prime numbers, one can speed them up in practice by performing a faster probabilistic test to quickly eliminate most composite numbers before switching to a guaranteed-correct algorithm to verify that the remaining numbers are prime.

The following table lists some of these tests. Their running time is given in terms of n, the number to be tested and, for probabilistic algorithms, the number k of tests performed. Moreover, ε is an arbitrarily small positive number, and log is the logarithm to an unspecified base. The big O notation means that each time bound should be multiplied by a constant factor to convert it from dimensionless units to units of time; this factor depends on implementation details such as the type of computer used to run the algorithm, but not on the input parameters n and k.

Test	Developed in	Type	Running time	Notes	References
AKS primality test	2002	deterministic	O((log n)6+ε)
Elliptic curve primality proving	1977	deterministic	O((log n)5+ε) heuristically
Miller–Rabin primality test	1980	probabilistic	O(k · (log n)2+ε)	error probability 4−k
Solovay–Strassen primality test	1977	probabilistic	O(k · (log n)3)	error probability 2−k

Special-purpose algorithms and the largest known prime

Further information: List of prime numbers

In addition to the aforementioned tests that apply to any natural number n, there are very efficient (deterministic) primality tests if the complete factorization of either n − 1 or n + 1 is known. For example, the Lucas primality test requires the knowledge of the prime factors of n − 1. This test can be applied to check whether

n! ± 1 = 1 · 2 · 3 · ... · n ± 1

are prime. Prime numbers of this form are known as factorial primes. Other primes where either p + 1 or p − 1 is of a particular shape include the Sophie Germain primes (primes of the form 2p + 1 with p prime), primorial primes, Fermat primes and Mersenne primes, that is, prime numbers that are of the form 2^p − 1, where p is an arbitrary prime. The Lucas–Lehmer test is particularly fast for numbers of this form. This is why the largest known prime has almost always been a Mersenne prime since the dawn of electronic computers.

If only a partial factorization of n − 1 or n + 1 is known, there are extensions of these methods that may be able to prove that n is prime.

The following table gives the largest known primes of the mentioned types. Some of these primes have been found using distributed computing. In 2009, the Great Internet Mersenne Prime Search project was awarded a US$100,000 prize for first discovering a prime with at least 10 million digits. The Electronic Frontier Foundation also offers $150,000 and $250,000 for primes with at least 100 million digits and 1 billion digits, respectively. Some of the largest primes not known to have any particular form (that is, no simple formula such as that of Mersenne primes) have been found by taking a piece of semi-random binary data, converting it to a number n, multiplying it by 256^k for some positive integer k, and searching for possible primes within the interval [256^kn + 1, 256^k(n + 1) − 1].

Type	Prime	Number of decimal digits	Date	Found by
Mersenne prime	277,232,917 − 1	23,249,425	December 26, 2017	Jonathan Pace, Great Internet Mersenne Prime Search
not a Mersenne prime (Proth number)	10,223 × 231,172,165 + 1	9,383,761	October 31, 2016	Péter Szabolcs, PrimeGrid
factorial prime	208,003! − 1	1,015,843	July 2016	Sou Fukui
primorial prime	1,098,133# − 1	476,311	March 2012	James P. Burt, PrimeGrid
twin primes	2,996,863,034,895  × 21,290,000 ± 1	388,342	September 2016	Tom Greer, PrimeGrid

Integer factorization

Main article: Integer factorization

Given a composite integer n, the task of providing one (or all) prime factors is referred to as factorization of n. Elliptic curve factorization is an algorithm relying on arithmetic on an elliptic curve.

Distribution

In 1975, number theorist Don Zagier commented that primes both

grow like weeds among the natural numbers, seeming to obey no other law than that of chance [but also] exhibit stunning regularity [and] that there are laws governing their behavior, and that they obey these laws with almost military precision.

The distribution of primes in the large, such as the question how many primes are smaller than a given, large threshold, is described by the prime number theorem, but no efficient formula for the n-th prime is known.

There are arbitrarily long sequences of consecutive non-primes, as for every positive integer $n$ the $n$ consecutive integers from $(n+1)!+2$ to $(n+1)!+n+1$ (inclusive) are all composite (as $(n+1)!+k$ is divisible by $k$ for $k$ between $2$ and $n+1$).

Dirichlet's theorem on arithmetic progressions, in its basic form, asserts that linear polynomials

$p(n)=a+bn$

with coprime integers a and b take infinitely many prime values. Stronger forms of the theorem state that the sum of the reciprocals of these prime values diverges, and that different such polynomials with the same b have approximately the same proportions of primes.

The corresponding question for quadratic polynomials is less well understood.

Formulas for primes

Main article: Formulas for primes

There is no known efficient formula for primes. For example, there is no non-constant polynomial, even in several variables, that takes only prime values. However, there are numerous expressions that do encode all primes, or only primes. One possible formula is based on Wilson's theorem and generates the number 2 many times and all other primes exactly once. There is also a set of Diophantine equations in 9 variables and one parameter with the following property: the parameter is prime if and only if the resulting system of equations has a solution over the natural numbers. This can be used to obtain a single formula with the property that all its positive values are prime.

Other examples of prime-generating formulas come from Mills' theorem and a theorem of Wright. These assert that there are real constants A > 1 and μ such that

$\left\lfloor A^{3^{n}}\right\rfloor {\text{ and }}\left\lfloor 2^{\cdots ^{2^{2^{\mu }}}}\right\rfloor$

are prime for any natural number n in the first formula, and any number of exponents in the second formula. Here $\lfloor \,\cdot \,\rfloor$ represents the floor function, i.e., the largest integer not greater than the number in question. However, computing A or μ requires the knowledge of infinitely many primes to begin with.

Number of prime numbers below a given number

Main articles: Prime number theorem and Prime-counting function

A chart depicting the prime counting function π(n) (blue), n/ln n (green) and Li(n) (red).
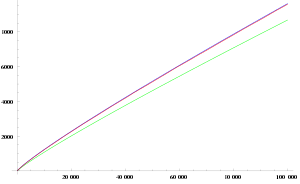
[(red) and (blue) almost coinciding within the picture]

The prime counting function π(n) is defined as the number of primes not greater than n. For example, π(11) = 5, since there are five primes less than or equal to 11. There are known algorithms to compute exact values of π(n) faster than it would be possible to compute each prime up to n. The prime number theorem states that π(n) satisfies

$\pi (n)\sim {\frac {n}{\ln n}},$

which means that the ratio of π(n) and the right hand fraction approaches 1 when n grows to infinity. This implies that the likelihood that a number less than n is prime is (approximately) inversely proportional to the number of digits in n. A more accurate estimate for π(n) is given by the offset logarithmic integral

$\operatorname {Li} (n)=\int _{2}^{n}{\frac {dt}{\ln t}}.$

The prime number theorem also implies estimates for the size of the n-th prime number p_n (i.e., p₁ = 2, p₂ = 3, etc.): up to a bounded factor, p_n grows like n log(n). In particular, the prime gaps, i.e. the differences p_n − p_n−1 of two consecutive primes become arbitrarily large. This latter statement can also be seen in a more elementary way by noting that the sequence n! + 2, n! + 3, …, n! + n consists of n − 1 composite numbers, for any natural number n. However, n − 1 composite numbers do make up gaps much smaller than n!. For example, with n − 1 = 7, the first prime gap of 8 is between the primes 89 and 97 while 8! = 40320.

Arithmetic progressions

An arithmetic progression is the set of natural numbers that give the same remainder when divided by some fixed number q called modulus. For example,

3, 12, 21, 30, 39, ...,

is an arithmetic progression modulo q = 9. Except for 3, none of these numbers is prime, since 3 + 9n = 3(1 + 3n) so that the remaining numbers in this progression are all composite. (In general terms, all prime numbers above q are of the form q#·n + m, where 0 < m < q#, and m has no prime factor ≤ q.) Thus, the progression

a, a + q, a + 2q, a + 3q, …

can have infinitely many primes only when a and q are coprime, i.e., their greatest common divisor is one. If this necessary condition is satisfied, Dirichlet's theorem on arithmetic progressions asserts that the progression contains infinitely many primes.

A demonstration of the artihmetic progression modulo 9. Prime numbers are highlighted in red. The rows (progressions) starting with a = 3, 6, or 9 contain at most one prime number. In all other rows (a = 1, 2, 4, 5, 7, and 8) there are infinitely many prime numbers. What is more, the primes are distributed equally among those rows in the long run—the density of all primes congruent to a modulo 9 is 1/6.

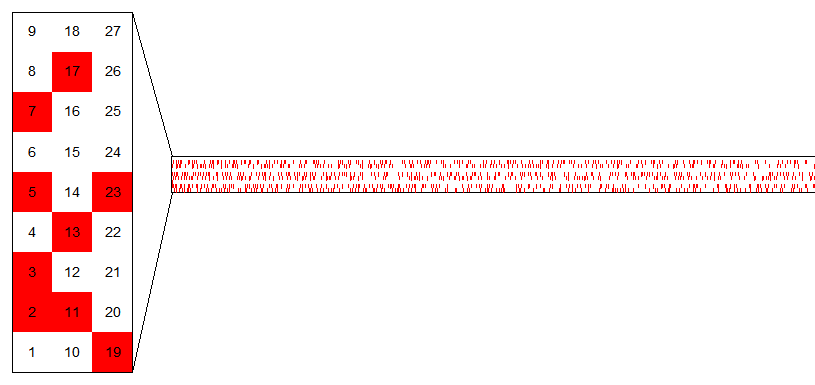
The Green–Tao theorem shows that there are arbitrarily long arithmetic progressions consisting of primes. An odd prime p is expressible as the sum of two squares, p = x² + y², exactly if p is congruent 1 modulo 4 (Fermat's theorem on sums of two squares).

Prime values of quadratic polynomials

The Ulam spiral. Prime numbers (highlighted in red) cluster on some diagonals and not others. Primes values of the quadratic polynomial 4n² - 2n + 41, as one such example, are highlighted in blue.

Euler noted that the function

$n^{2}+n+41$

yields prime numbers for 0 ≤ n < 40, a fact leading into deep algebraic number theory: more specifically, Heegner numbers. For greater n, the expression also produces composite values. The Hardy-Littlewood conjecture F makes an asymptotic prediction about the density of primes among the values of quadratic polynomials (with integer coefficients a, b, and c),

$f(n)=ax^{2}+bx+c,$

in terms of Li(n) and the coefficients a, b, and c. However, progress has been difficult. No quadratic polynomial (with a ≠ 0) is known to take infinitely many prime values.

The Ulam spiral depicts all natural numbers in a spiral-like way. Primes cluster on certain diagonals and not others, suggesting that some quadratic polynomials take prime values more often than others. The example below displays concentrations of prime numbers (blue background) from 41 to 1001 arranged in an Ulam spiral with a start value of 41 (green background numbers are numbers with just 3 divisors, and red background are numbers with a large number of divisors).

Open questions

Zeta function and the Riemann hypothesis

Main article: Riemann hypothesis

Plot of the zeta function ζ(s). At s = 1, the function has a pole, that is to say, it tends to infinity.

The Riemann zeta function ζ(s) is defined as an infinite sum

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}},$

where s is a complex number with real part bigger than 1. It is a consequence of the fundamental theorem of arithmetic that this sum agrees with the infinite product

$\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}.$

The zeta function is closely related to prime numbers. For example, the aforementioned fact that there are infinitely many primes can also be seen using the zeta function: if there were only finitely many primes then ζ(1) would have a finite value. However, the harmonic series 1 + 1/2 + 1/3 + 1/4 + ... diverges (i.e., exceeds any given number), so there must be infinitely many primes. Another example of the richness of the zeta function and a glimpse of modern algebraic number theory is the following identity (Basel problem), due to Euler,

$\zeta (2)=\prod _{p}{\frac {1}{1-p^{-2}}}={\frac {\pi ^{2}}{6}}.$

The reciprocal of ζ(2), 6/π², is the probability that two numbers selected at random are relatively prime.

The unproven Riemann hypothesis, dating from 1859, states that except for s = −2, −4, ..., all zeroes of the ζ-function have real part equal to 1/2. The connection to prime numbers is that it essentially says that the primes are as regularly distributed as possible. From a physical viewpoint, it roughly states that the irregularity in the distribution of primes only comes from random noise. From a mathematical viewpoint, it roughly states that the asymptotic distribution of primes (about x/log x of numbers less than x are primes, the prime number theorem) also holds for much shorter intervals of length about the square root of x (for intervals near x). This hypothesis is generally believed to be correct. In particular, the simplest assumption is that primes should have no significant irregularities without good reason.

Other conjectures

Further information: Category:Conjectures about prime numbers

In addition to the Riemann hypothesis, many more conjectures revolving about primes have been posed. Often having an elementary formulation, many of these conjectures have withstood a proof for decades: all four of Landau's problems from 1912 are still unsolved. One of them is Goldbach's conjecture, which asserts that every even integer n greater than 2 can be written as a sum of two primes. As of February 2011, this conjecture has been verified for all numbers up to n = 2 · 10¹⁷. Weaker statements than this have been proven, for example Vinogradov's theorem says that every sufficiently large odd integer can be written as a sum of three primes. Chen's theorem says that every sufficiently large even number can be expressed as the sum of a prime and a semiprime, the product of two primes. Also, any even integer can be written as the sum of six primes. The branch of number theory studying such questions is called additive number theory.

Other conjectures deal with the question whether an infinity of prime numbers subject to certain constraints exists. It is conjectured that there are infinitely many Fibonacci primes and infinitely many Mersenne primes, but not Fermat primes. It is not known whether or not there are an infinite number of Wieferich primes and of prime Euclid numbers.

A third type of conjectures concerns aspects of the distribution of primes. It is conjectured that there are infinitely many twin primes, pairs of primes with difference 2 (twin prime conjecture). Polignac's conjecture is a strengthening of that conjecture, it states that for every positive integer n, there are infinitely many pairs of consecutive primes that differ by 2n. It is conjectured there are infinitely many primes of the form n² + 1. These conjectures are special cases of the broad Schinzel's hypothesis H. Brocard's conjecture says that there are always at least four primes between the squares of consecutive primes greater than 2. Legendre's conjecture states that there is a prime number between n² and (n + 1)² for every positive integer n. It is implied by the stronger Cramér's conjecture.

Applications

For a long time, number theory in general, and the study of prime numbers in particular, was seen as the canonical example of pure mathematics, with no applications outside of the self-interest of studying the topic with the exception of use of prime numbered gear teeth to distribute wear evenly. In particular, number theorists such as British mathematician G. H. Hardy prided themselves on doing work that had absolutely no military significance. However, this vision was shattered in the 1970s, when it was publicly announced that prime numbers could be used as the basis for the creation of public key cryptography algorithms. Prime numbers are also used for hash tables and pseudorandom number generators.

Some rotor machines were designed with a different number of pins on each rotor, with the number of pins on any one rotor either prime, or coprime to the number of pins on any other rotor. This helped generate the full cycle of possible rotor positions before repeating any position.

The International Standard Book Numbers work with a check digit, which exploits the fact that 11 is a prime.

Arithmetic modulo a prime and finite fields

Main article: Modular arithmetic

Modular arithmetic modifies usual arithmetic by only using the numbers

$\{0,1,2,\dots ,n-1\},$

where n is a fixed natural number called modulus. Calculating sums, differences and products is done as usual, but whenever a negative number or a number greater than n − 1 occurs, it gets replaced by the remainder after division by n. For instance, for n = 7, the sum 3 + 5 is 1 instead of 8, since 8 divided by 7 has remainder 1. This is referred to by saying "3 + 5 is congruent to 1 modulo 7" and is denoted

$3+5\equiv 1{\pmod {7}}.$

Similarly, 6 + 1 ≡ 0 (mod 7), 2 − 5 ≡ 4 (mod 7), since −3 + 7 = 4, and 3 · 4 ≡ 5 (mod 7) as 12 has remainder 5. Standard properties of addition and multiplication familiar from the integers remain valid in modular arithmetic. In the parlance of abstract algebra, the above set of integers, which is also denoted Z/nZ, is therefore a commutative ring for any n. Division, however, is not in general possible in this setting. For example, for n = 6, the equation

$3\cdot x\equiv 2{\pmod {6}},$

a solution x of which would be an analogue of 2/3, cannot be solved, as one can see by calculating 3 · 0, ..., 3 · 5 modulo 6. The distinctive feature of prime numbers is the following: division is possible in modular arithmetic if and only if n is a prime. Equivalently, n is prime if and only if all integers m satisfying 2 ≤ m ≤ n − 1 are coprime to n, i.e. their only common divisor is one. Indeed, for n = 7, the equation

$3\cdot x\equiv 2{\pmod {7}},$

has a unique solution, x = 3. Because of this, for any prime p, Z/pZ (also denoted F_p) is called a field or, more specifically, a finite field since it contains finitely many, namely p, elements.

A number of theorems can be derived from inspecting F_p in this abstract way. For example, Fermat's little theorem, stating

$a^{p-1}\equiv 1{\pmod {p}}$

for any integer a not divisible by p, may be proved using these notions. This implies

$\sum _{a=1}^{p-1}a^{p-1}\equiv (p-1)\cdot 1\equiv -1{\pmod {p}}.$

Giuga's conjecture says that this equation is also a sufficient condition for p to be prime. Another consequence of Fermat's little theorem is the following: if p is a prime number other than 2 and 5, ¹/_p is always a recurring decimal, whose period is p − 1 or a divisor of p − 1. The fraction ¹/_p expressed likewise in base q (rather than base 10) has similar effect, provided that p is not a prime factor of q. Wilson's theorem says that an integer p > 1 is prime if and only if the factorial (p − 1)! + 1 is divisible by p. Moreover, an integer n > 4 is composite if and only if (n − 1)! is divisible by n.

Fermat primes and constructible polygons

Construction of a regular pentagon using straightedge and compass. This is only possible because 5 is a Fermat prime.

Fermat primes are primes of the form

F_k = 2^2k + 1,

with k a natural number. They are named after Pierre de Fermat, who conjectured that all such numbers are prime. This was based on the evidence of the first five numbers in this series—3, 5, 17, 257, and 65,537—being prime. However, F₅ is composite and so are all other Fermat numbers that have been verified as of 2015. A regular n-gon is constructible using straightedge and compass if and only if the odd prime factors of n (if any) are distinct Fermat primes.

Other mathematical occurrences of primes

Many mathematical domains make great use of prime numbers. An example from the theory of finite groups are the Sylow theorems: if G is a finite group and pⁿ is the highest power of the prime p that divides the order of G, then G has a subgroup of order pⁿ. Also, any group of prime order is cyclic (Lagrange's theorem) and any group whose order is divisible by only two primes is solvable (the Burnside theorem).

Public-key cryptography

Main article: Public-key cryptography

Several public-key cryptography algorithms, such as RSA and the Diffie–Hellman key exchange, are based on large prime numbers (2048-bit primes are common). RSA relies on the assumption that it is much easier (i.e., more efficient) to perform the multiplication of two (large) numbers x and y than to calculate x and y (assumed coprime) if only the product xy is known. The Diffie–Hellman key exchange relies on the fact that there are efficient algorithms for modular exponentiation, while the reverse operation the discrete logarithm is thought to be a hard problem.

Prime numbers in nature

The evolutionary strategy used by cicadas of the genus Magicicada make use of prime numbers. These insects spend most of their lives as grubs underground. They only pupate and then emerge from their burrows after 7, 13 or 17 years, at which point they fly about, breed, and then die after a few weeks at most. The logic for this is believed to be that the prime number intervals between emergences make it very difficult for predators to evolve that could specialize as predators on Magicicadas. If Magicicadas appeared at a non-prime number intervals, say every 12 years, then predators appearing every 2, 3, 4, 6, or 12 years would be sure to meet them. Over a 200-year period, average predator populations during hypothetical outbreaks of 14- and 15-year cicadas would be up to 2% higher than during outbreaks of 13- and 17-year cicadas. Though small, this advantage appears to have been enough to drive natural selection in favour of a prime-numbered life-cycle for these insects.

There is speculation that the zeros of the zeta function are connected to the energy levels of complex quantum systems.

Generalizations

The concept of prime number is so important that it has been generalized in different ways in various branches of mathematics. Generally, "prime" indicates minimality or indecomposability, in an appropriate sense. For example, the prime field is the smallest subfield of a field F containing both 0 and 1. It is either Q or the finite field with p elements, whence the name. Often a second, additional meaning is intended by using the word prime, namely that any object can be, essentially uniquely, decomposed into its prime components. For example, in knot theory, a prime knot is a knot that is indecomposable in the sense that it cannot be written as the knot sum of two nontrivial knots. Any knot can be uniquely expressed as a connected sum of prime knots. Prime models and prime 3-manifolds are other examples of this type.

Prime elements in rings

Main articles: Prime element and Irreducible element

Prime numbers give rise to two more general concepts that apply to elements of any commutative ring R, an algebraic structure where addition, subtraction and multiplication are defined: prime elements and irreducible elements. An element p of R is called prime element if it is neither zero nor a unit (i.e., does not have a multiplicative inverse) and satisfies the following requirement: given x and y in R such that p divides the product xy, then p divides x or y. An element is irreducible if it is not a unit and cannot be written as a product of two ring elements that are not units. In the ring Z of integers, the set of prime elements equals the set of irreducible elements, which is

$\{\dots ,-11,-7,-5,-3,-2,2,3,5,7,11,\dots \}\,.$

In any ring R, any prime element is irreducible. The converse does not hold in general, but does hold for unique factorization domains.

The fundamental theorem of arithmetic continues to hold in unique factorization domains. An example of such a domain is the Gaussian integers Z[i], that is, the set of complex numbers of the form a + bi where i denotes the imaginary unit and a and b are arbitrary integers. Its prime elements are known as Gaussian primes. Not every prime (in Z) is a Gaussian prime: in the bigger ring Z[i], 2 factors into the product of the two Gaussian primes (1 + i) and (1 − i). Rational primes (i.e. prime elements in Z) of the form 4k + 3 are Gaussian primes, whereas rational primes of the form 4k + 1 are not.

Prime ideals

Main article: Prime ideals

In ring theory, the notion of number is generally replaced with that of ideal. Prime ideals, which generalize prime elements in the sense that the principal ideal generated by a prime element is a prime ideal, are an important tool and object of study in commutative algebra, algebraic number theory and algebraic geometry. The prime ideals of the ring of integers are the ideals (0), (2), (3), (5), (7), (11), … The fundamental theorem of arithmetic generalizes to the Lasker–Noether theorem, which expresses every ideal in a Noetherian commutative ring as an intersection of primary ideals, which are the appropriate generalizations of prime powers.

Prime ideals are the points of algebro-geometric objects, via the notion of the spectrum of a ring. Arithmetic geometry also benefits from this notion, and many concepts exist in both geometry and number theory. For example, factorization or ramification of prime ideals when lifted to an extension field, a basic problem of algebraic number theory, bears some resemblance with ramification in geometry. Such ramification questions occur even in number-theoretic questions solely concerned with integers. For example, prime ideals in the ring of integers of quadratic number fields can be used in proving quadratic reciprocity, a statement that concerns the solvability of quadratic equations

$x^{2}\equiv p{\pmod {q}},$

where x is an integer and p and q are (usual) prime numbers. Early attempts to prove Fermat's Last Theorem climaxed when Kummer introduced regular primes, primes satisfying a certain requirement concerning the failure of unique factorization in the ring consisting of expressions

$a_{0}+a_{1}\zeta +\cdots +a_{p-1}\zeta ^{p-1}\,,$

where a₀, ..., a_p−1 are integers and ζ is a complex number such that ζ^p = 1.

Valuations

Valuation theory studies certain functions from a field K to the real numbers R called valuations. Every such valuation yields a topology on K, and two valuations are called equivalent if they yield the same topology. A prime of K (sometimes called a place of K) is an equivalence class of valuations. For example, the p-adic valuation of a rational number q is defined to be the integer v_p(q), such that

$q=p^{v_{p}(q)}{\frac {r}{s}},$

where both r and s are not divisible by p. For example, v₃(18/7) = 2. The p-adic norm is defined as

$\left|q\right|_{p}:=p^{-v_{p}(q)}.$

In particular, this norm gets smaller when a number is multiplied by p, in sharp contrast to the usual absolute value (also referred to as the infinite prime). While completing Q (roughly, filling the gaps) with respect to the absolute value yields the field of real numbers, completing with respect to the p-adic norm |−|_p yields the field of p-adic numbers. These are essentially all possible ways to complete Q, by Ostrowski's theorem. Certain arithmetic questions related to Q or more general global fields may be transferred back and forth to the completed (or local) fields. This local-global principle again underlines the importance of primes to number theory.

In games, arts, and literature

Prime numbers have influenced many artists and writers. The French composer Olivier Messiaen used prime numbers to create ametrical music through "natural phenomena". In works such as La Nativité du Seigneur (1935) and Quatre études de rythme (1949–50), he simultaneously employs motifs with lengths given by different prime numbers to create unpredictable rhythms: the primes 41, 43, 47 and 53 appear in the third étude, "Neumes rythmiques". According to Messiaen this way of composing was "inspired by the movements of nature, movements of free and unequal durations".

In his science fiction novel Contact, NASA scientist Carl Sagan suggested that prime numbers could be used as a means of communicating with aliens, an idea that he had first developed informally with American astronomer Frank Drake in 1975. In the novel The Curious Incident of the Dog in the Night-Time by Mark Haddon, the narrator arranges the sections of the story by consecutive prime numbers.

Many films, such as Cube, Sneakers, The Mirror Has Two Faces and A Beautiful Mind reflect a popular fascination with the mysteries of prime numbers and cryptography. Prime numbers are used as a metaphor for loneliness and isolation in the Paolo Giordano novel The Solitude of Prime Numbers, in which they are portrayed as "outsiders" among integers.

See also

• Bonse's inequality
• Chebotarev's density theorem
• Cullen number
• Illegal prime
• Number field sieve
• Practical number
• Prime k-tuple
• Ramanujan prime
• RSA number
• Smooth number
• Super-prime

External links

• "Prime number", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Caldwell, Chris, The Prime Pages at primes.utm.edu.
• Prime Numbers on In Our Time at the BBC
• Plus teacher and student package: prime numbers from Plus, the free online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge.

Prime number generators and calculators

• Prime Number Checker identifies the smallest prime factor of a number.
• Fast Online primality test with factorization makes use of the Elliptic Curve Method (up to thousand-digits numbers, requires Java).
• Huge database of prime numbers
• Prime Numbers up to 1 trillion