Archimedean solid
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids (each with only one type of polygon face), and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive.[1] An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.
In these polyhedra, the vertices are identical, in the sense that a global isometry of the entire solid takes any one vertex to any other. Branko Grünbaum (2009) observed that a 14th polyhedron, the elongated square gyrobicupola (or pseudo-rhombicuboctahedron), meets a weaker definition of an Archimedean solid, in which "identical vertices" means merely that the parts of the polyhedron near any two vertices look the same (they have the same shapes of faces meeting around each vertex in the same order and forming the same angles). Grünbaum pointed out a frequent error in which authors define Archimedean solids using some form of this local definition but omit the 14th polyhedron. If only 13 polyhedra are to be listed, the definition must use global symmetries of the polyhedron rather than local neighborhoods.
Prisms and antiprisms, whose symmetry groups are the dihedral groups, are generally not considered to be Archimedean solids, even though their faces are regular polygons and their symmetry groups act transitively on their vertices. Excluding these two infinite families, there are 13 Archimedean solids. All the Archimedean solids (but not the elongated square gyrobicupola) can be made via Wythoff constructions from the Platonic solids with tetrahedral, octahedral and icosahedral symmetry.
Origin of name
[edit]The Archimedean solids take their name from Archimedes, who discussed them in a now-lost work. Pappus refers to it, stating that Archimedes listed 13 polyhedra.[2] During the Renaissance, artists and mathematicians valued pure forms with high symmetry, and by around 1620 Johannes Kepler had completed the rediscovery of the 13 polyhedra,[3] as well as defining the prisms, antiprisms, and the non-convex solids known as Kepler-Poinsot polyhedra. (See Schreiber, Fischer & Sternath 2008 for more information about the rediscovery of the Archimedean solids during the renaissance.)
Kepler may have also found the elongated square gyrobicupola (pseudorhombicuboctahedron): at least, he once stated that there were 14 Archimedean solids. However, his published enumeration only includes the 13 uniform polyhedra, and the first clear statement of the pseudorhombicuboctahedron's existence was made in 1905, by Duncan Sommerville.[2]
Classification
[edit]There are 13 Archimedean solids (not counting the elongated square gyrobicupola; 15 if the mirror images of two enantiomorphs, the snub cube and snub dodecahedron, are counted separately).
Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration of 4.6.8 means that a square, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).
| Name/ (alternative name) |
Schläfli Coxeter |
Transparent | Solid | Net | Vertex conf./fig. |
Faces | Edges | Vert. | Volume (unit edges) |
Point group |
Sphericity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Truncated tetrahedron | t{3,3} |
 |

|
3.6.6
|
8 | 4 triangles 4 hexagons |
18 | 12 | 2.710576 | Td | 0.7754132 | |
| Cuboctahedron (rhombitetratetrahedron, triangular gyrobicupola) |
r{4,3} or rr{3,3} |
 |

|

|
3.4.3.4
|
14 | 8 triangles 6 squares |
24 | 12 | 2.357023 | Oh | 0.9049972 |
| Truncated cube | t{4,3} |
 |

|
3.8.8
|
14 | 8 triangles 6 octagons |
36 | 24 | 13.599663 | Oh | 0.8494937 | |
| Truncated octahedron (truncated tetratetrahedron) |
t{3,4} or tr{3,3} |
 |

|

|
4.6.6
|
14 | 6 squares 8 hexagons |
36 | 24 | 11.313709 | Oh | 0.9099178 |
| Rhombicuboctahedron (small rhombicuboctahedron, elongated square orthobicupola) |
rr{4,3} |
 |

|
3.4.4.4
|
26 | 8 triangles 18 squares |
48 | 24 | 8.714045 | Oh | 0.9540796 | |
| Truncated cuboctahedron (great rhombicuboctahedron) |
tr{4,3} |
 |

|
4.6.8
|
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | 41.798990 | Oh | 0.9431657 | |
| Snub cube (snub cuboctahedron) |
sr{4,3} |
 |

|
3.3.3.3.4
|
38 | 32 triangles 6 squares |
60 | 24 | 7.889295 | O | 0.9651814 | |
| Icosidodecahedron (pentagonal gyrobirotunda) |
r{5,3} |
 |

|
3.5.3.5
|
32 | 20 triangles 12 pentagons |
60 | 30 | 13.835526 | Ih | 0.9510243 | |
| Truncated dodecahedron | t{5,3} |
 |

|
3.10.10
|
32 | 20 triangles 12 decagons |
90 | 60 | 85.039665 | Ih | 0.9260125 | |
| Truncated icosahedron | t{3,5} |
 |

|
5.6.6
|
32 | 12 pentagons 20 hexagons |
90 | 60 | 55.287731 | Ih | 0.9666219 | |
| Rhombicosidodecahedron (small rhombicosidodecahedron) |
rr{5,3} |
 |

|
3.4.5.4
|
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | 41.615324 | Ih | 0.9792370 | |
| Truncated icosidodecahedron (great rhombicosidodecahedron) |
tr{5,3} |
 |

|
4.6.10
|
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | 206.803399 | Ih | 0.9703127 | |
| Snub dodecahedron (snub icosidodecahedron) |
sr{5,3} |
 |

|
3.3.3.3.5
|
92 | 80 triangles 12 pentagons |
150 | 60 | 37.616650 | I | 0.9820114 | |
Some definitions of semiregular polyhedron include one more figure, the elongated square gyrobicupola or "pseudo-rhombicuboctahedron".[4]
Properties
[edit]The number of vertices is 720° divided by the vertex angle defect.
The cuboctahedron and icosidodecahedron are edge-uniform and are called quasi-regular.
The duals of the Archimedean solids are called the Catalan solids. Together with the bipyramids and trapezohedra, these are the face-uniform solids with regular vertices.
Chirality
[edit]The snub cube and snub dodecahedron are known as chiral, as they come in a left-handed form (Latin: levomorph or laevomorph) and right-handed form (Latin: dextromorph). When something comes in multiple forms which are each other's three-dimensional mirror image, these forms may be called enantiomorphs. (This nomenclature is also used for the forms of certain chemical compounds.)
Construction of Archimedean solids
[edit]
The different Archimedean and Platonic solids can be related to each other using a handful of general constructions. Starting with a Platonic solid, truncation involves cutting away of corners. To preserve symmetry, the cut is in a plane perpendicular to the line joining a corner to the center of the polyhedron and is the same for all corners. Depending on how much is truncated (see table below), different Platonic and Archimedean (and other) solids can be created. If the truncation is exactly deep enough such that each pair of faces from adjacent vertices shares exactly one point, it is known as a rectification. An expansion, or cantellation, involves moving each face away from the center (by the same distance so as to preserve the symmetry of the Platonic solid) and taking the convex hull. Expansion with twisting also involves rotating the faces, thus splitting each rectangle corresponding to an edge into two triangles by one of the diagonals of the rectangle. The last construction we use here is truncation of both corners and edges. Ignoring scaling, expansion can also be viewed as the rectification of the rectification. Likewise, the cantitruncation can be viewed as the truncation of the rectification.
Note the duality between the cube and the octahedron, and between the dodecahedron and the icosahedron. Also, partially because the tetrahedron is self-dual, only one Archimedean solid that has at most tetrahedral symmetry. (All Platonic solids have at least tetrahedral symmetry, as tetrahedral symmetry is a symmetry operation of (i.e. is included in) octahedral and isohedral symmetries, which is demonstrated by the fact that an octahedron can be viewed as a rectified tetrahedron, and an icosahedron can be used as a snub tetrahedron.)
Stereographic projection
[edit]| truncated tetrahedron | truncated cube | truncated octahedron | truncated dodecahedron | truncated icosahedron | |||||
|---|---|---|---|---|---|---|---|---|---|
 triangle-centered |
 hexagon-centered |
 octagon-centered |
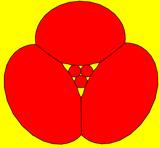 triangle-centered |
 square-centered |
 hexagon-centered |
 Decagon-centered |
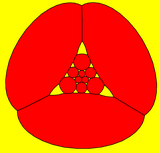 Triangle-centered |
 pentagon-centered |
 hexagon-centered |
| cuboctahedron | icosidodecahedron | rhombicuboctahedron | rhombicosidodecahedron | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 square-centered |
 triangle-centered |
 vertex-centered |
 pentagon-centered |
 triangle-centered |
 square-centered |
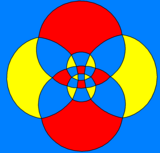 square-centered |
 triangle-centered |
 Pentagon-centered |
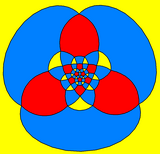 Triangle-centered |
 Square-centered | |||
| truncated cuboctahedron | truncated icosidodecahedron | snub cube | ||||
|---|---|---|---|---|---|---|
 square-centered |
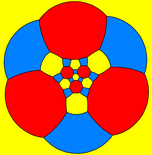 hexagon-centered |
 octagon-centered |
 decagon-centered |
 hexagon-centered |
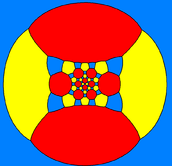 square-centered |
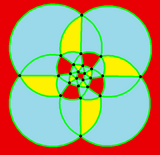 square-centered |
See also
[edit]- Aperiodic tiling
- Archimedean graph
- Icosahedral twins
- List of uniform polyhedra
- Prince Rupert's cube#Generalizations
- Quasicrystal
- Regular polyhedron
- Semiregular polyhedron
- Toroidal polyhedron
- Uniform polyhedron
Citations
[edit]- ^ Steckles, Katie (20 December 2018). "The Unwanted Shape". YouTube. Retrieved 20 January 2022.
- ^ a b Grünbaum (2009).
- ^ Field J., Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences, 50, 1997, 227
- ^ Malkevitch (1988), p. 85
Works cited
[edit]- Grünbaum, Branko (2009), "An enduring error", Elemente der Mathematik, 64 (3): 89–101, doi:10.4171/EM/120, MR 2520469. Reprinted in Pitici, Mircea, ed. (2011), The Best Writing on Mathematics 2010, Princeton University Press, pp. 18–31.
- Malkevitch, Joseph (1988), "Milestones in the history of polyhedra", in Senechal, M.; Fleck, G. (eds.), Shaping Space: A Polyhedral Approach, Boston: Birkhäuser, pp. 80–92.
General references
[edit]- Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. 89 (514): 76–81. doi:10.1017/S0025557200176818. S2CID 125675814..
- Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3–9)
- Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (2008). "New light on the rediscovery of the Archimedean solids during the renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. Bibcode:2008AHES...62..457S. doi:10.1007/s00407-008-0024-z. ISSN 0003-9519. S2CID 122216140..
External links
[edit]- Weisstein, Eric W. "Archimedean solid". MathWorld.
- Archimedean Solids by Eric W. Weisstein, Wolfram Demonstrations Project.
- Paper models of Archimedean Solids and Catalan Solids
- Free paper models(nets) of Archimedean solids
- The Uniform Polyhedra by Dr. R. Mäder
- Archimedean Solids at Visual Polyhedra by David I. McCooey
- Virtual Reality Polyhedra, The Encyclopedia of Polyhedra by George W. Hart
- Penultimate Modular Origami by James S. Plank
- Interactive 3D polyhedra in Java
- Solid Body Viewer is an interactive 3D polyhedron viewer which allows you to save the model in svg, stl or obj format.
- Stella: Polyhedron Navigator: Software used to create many of the images on this page.
- Paper Models of Archimedean (and other) Polyhedra


























