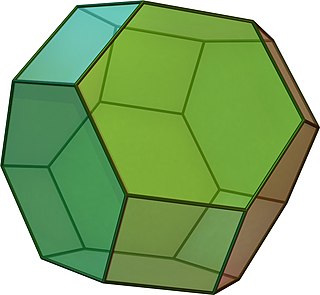
Truncated octahedron

Truncated octahedral graph
Truncated octahedral graph
	3-fold symmetric Schlegel diagram
Vertices	24
Edges	36
Automorphisms	48
Chromatic number	2
Book thickness	3
Queue number	2
Properties	Cubic, Hamiltonian, regular, zero-symmetric
	Table of graphs and parameters

Truncated octahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 14, E = 36, V = 24 (χ = 2)
Faces by sides	6{4}+8{6}
Conway notation	tO bT
Schläfli symbols	t{3,4} tr{3,3} or $t{\begin{Bmatrix}3\\3\end{Bmatrix}}$
Schläfli symbols	t_0,1{3,4} or t_0,1,2{3,3}
Wythoff symbol	2 4 \| 3 3 3 2 \|
Coxeter diagram
Symmetry group	O_h, B₃, [4,3], (432), order 48 T_h, [3,3] and (332), order 24
Rotation group	O, [4,3]⁺, (432), order 24
Dihedral angle	${\begin{aligned}{\text{4-6:}}&\ \arccos {\tfrac {-1}{\sqrt {3}}}=125^{\circ }15'51''\\{\text{6-6:}}&\ \arccos {\tfrac {-1}{3}}=109^{\circ }28'16''\end{aligned}}$
References	U₀₈, C₂₀, W₇
Properties	Semiregular convex parallelohedron permutohedron zonohedron
Colored faces	4.6.6 (Vertex figure)
Tetrakis hexahedron (dual polyhedron)	Net

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron. It is also the Goldberg polyhedron G_IV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron.

The truncated octahedron was called the "mecon" by Buckminster Fuller.^[1]

Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths ⁠9/8⁠√2 and ⁠3/2⁠√2.

Construction

A truncated octahedron is constructed from a regular octahedron with side length 3a by the removal of six right square pyramids, one from each point. These pyramids have both base side length (a) and lateral side length (e) of a, to form equilateral triangles. The base area is then a². Note that this shape is exactly similar to half an octahedron or Johnson solid J₁.

From the properties of square pyramids, we can now find the slant height, s, and the height, h, of the pyramid:

{\begin{aligned}h&={\sqrt {e^{2}-{\tfrac {1}{2}}a^{2}}}&&={\tfrac {1}{\sqrt {2}}}a\\s&={\sqrt {h^{2}+{\tfrac {1}{4}}a^{2}}}&&={\sqrt {{\tfrac {1}{2}}a^{2}+{\tfrac {1}{4}}a^{2}}}&&={\tfrac {\sqrt {3}}{2}}a\end{aligned}}

The volume, V, of the pyramid is given by:

V={\tfrac {1}{3}}a^{2}h={\tfrac {\sqrt {2}}{6}}a^{3}

Because six pyramids are removed by truncation, there is a total lost volume of √2a³.

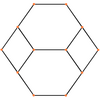
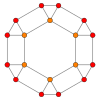
Orthogonal projections

The truncated octahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: Hexagon, and square. The last two correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections
Centered by	Vertex	Edge 4-6	Edge 6-6	Face Square	Face Hexagon
Solid
Wireframe
Dual
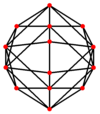
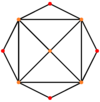
Projective symmetry	[2]	[2]	[2]	[4]	[6]

Spherical tiling

The truncated octahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Orthographic projection	Stereographic projections
	square-centered	hexagon-centered

Coordinates


Orthogonal projection in bounding box (±2,±2,±2)	Truncated octahedron with hexagons replaced by 6 coplanar triangles. There are 8 new vertices at: (±1,±1,±1).	Truncated octahedron subdivided into as a topological rhombic triacontahedron

All permutations of (0, ±1, ±2) are Cartesian coordinates of the vertices of a truncated octahedron of edge length a = √2 centered at the origin. The vertices are thus also the corners of 12 rectangles whose long edges are parallel to the coordinate axes.

The edge vectors have Cartesian coordinates (0, ±1, ±1) and permutations of these. The face normals (normalized cross products of edges that share a common vertex) of the 6 square faces are (0, 0, ±1), (0, ±1, 0) and (±1, 0, 0). The face normals of the 8 hexagonal faces are (±⁠1/√3⁠, ±⁠1/√3⁠, ±⁠1/√3⁠). The dot product between pairs of two face normals is the cosine of the dihedral angle between adjacent faces, either −⁠1/3⁠ or −⁠1/√3⁠. The dihedral angle is approximately 1.910633 radians (109.471° OEIS: A156546) at edges shared by two hexagons or 2.186276 radians (125.263° OEIS: A195698) at edges shared by a hexagon and a square.

Dissection

The truncated octahedron can be dissected into a central octahedron, surrounded by 8 triangular cupolae on each face, and 6 square pyramids above the vertices.^[2]

Removing the central octahedron and 2 or 4 triangular cupolae creates two Stewart toroids, with dihedral and tetrahedral symmetry:

Genus 2	Genus 3
D_3d, [2⁺,6], (2*3), order 12	T_d, [3,3], (*332), order 24

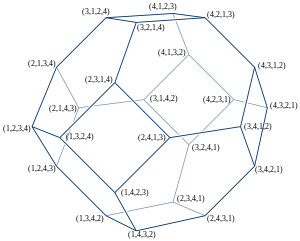
Permutohedron

The truncated octahedron can also be represented by even more symmetric coordinates in four dimensions: all permutations of (1, 2, 3, 4) form the vertices of a truncated octahedron in the three-dimensional subspace x + y + z + w = 10. Therefore, the truncated octahedron is the permutohedron of order 4: each vertex corresponds to a permutation of (1, 2, 3, 4) and each edge represents a single pairwise swap of two elements.

Area and volume

The surface area S and the volume V of a truncated octahedron of edge length a are:

{\begin{aligned}S&=\left(6+12{\sqrt {3}}\right)a^{2}&&\approx 26.784\,6097a^{2}\\V&=8{\sqrt {2}}a^{3}&&\approx 11.313\,7085a^{3}.\end{aligned}}

Uniform colorings

There are two uniform colorings, with tetrahedral symmetry and octahedral symmetry, and two 2-uniform coloring with dihedral symmetry as a truncated triangular antiprism. The constructional names are given for each. Their Conway polyhedron notation is given in parentheses.

1-uniform		2-uniform
O_h, [4,3], (*432) Order 48	T_d, [3,3], (*332) Order 24	D_4h, [4,2], (*422) Order 16	D_3d, [2⁺,6], (2*3) Order 12
122 coloring	123 coloring	122 & 322 colorings	122 & 123 colorings
Truncated octahedron (tO)	Bevelled tetrahedron (bT)	Truncated square bipyramid (tdP4)	Truncated triangular antiprism (tA3)

Chemistry

The truncated octahedron exists in the structure of the faujasite crystals.

Data Hiding

The truncated octahedron (in fact, the generalized truncated octahedron) appears in the error analysis of quantization index modulation (QIM) in conjunction with repetition coding.^[3]

Related polyhedra

The truncated octahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

It also exists as the omnitruncate of the tetrahedron family:

Family of uniform tetrahedral polyhedra
Symmetry: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Symmetry mutations

n32 symmetry mutation of omnitruncated tilings: 4.6.2n* v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

*nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n v t e
Symmetry *nn2 [n,n]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *nn2 [n,n]	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Figure
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Dual
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

This polyhedron is a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter–Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedra), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures n.6.6, extending into the hyperbolic plane:

*n32 symmetry mutation of truncated tilings: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures 4.2n.2n, extending into the hyperbolic plane:

*n42 symmetry mutation of truncated tilings: 4.2n.2n v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis figures
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Related polytopes

The truncated octahedron (bitruncated cube), is first in a sequence of bitruncated hypercubes:

Bitruncated hypercubes
Image							...
Name	Bitruncated cube	Bitruncated tesseract	Bitruncated 5-cube	Bitruncated 6-cube	Bitruncated 7-cube	Bitruncated 8-cube
Coxeter
Vertex figure	( )v{ }	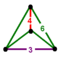{ }v{ }	{ }v{3}	{ }v{3,3}	{ }v{3,3,3}	{ }v{3,3,3,3}

It is possible to slice a tesseract by a hyperplane so that its sliced cross-section is a truncated octahedron.^[4]

Tessellations

The truncated octahedron exists in three different convex uniform honeycombs (space-filling tessellations):

Bitruncated cubic	Cantitruncated cubic	Truncated alternated cubic

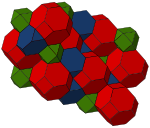
The cell-transitive bitruncated cubic honeycomb can also be seen as the Voronoi tessellation of the body-centered cubic lattice. The truncated octahedron is one of five three-dimensional primary parallelohedra.

Objects

Jungle gym nets often include truncated octahedra.

ancient Chinese die
sculpture in Bonn
Rubik's Cube variant
model made with Polydron construction set
Pyrite crystal

Truncated octahedral graph

In the mathematical field of graph theory, a truncated octahedral graph is the graph of vertices and edges of the truncated octahedron. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.^[5] It has book thickness 3 and queue number 2.^[6]

As a Hamiltonian cubic graph, it can be represented by LCF notation in multiple ways: [3, −7, 7, −3]⁶, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]², and [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3].^[7]

References

^ "Truncated Octahedron". Wolfram Mathworld.
^ Doskey, Alex. "Adventures Among the Toroids – Chapter 5 – Simplest (R)(A)(Q)(T) Toroids of genus p=1". www.doskey.com.
^ Perez-Gonzalez, F.; Balado, F.; Martin, J.R.H. (2003). "Performance analysis of existing and new methods for data hiding with known-host information in additive channels". IEEE Transactions on Signal Processing. 51 (4): 960–980. Bibcode:2003ITSP...51..960P. doi:10.1109/TSP.2003.809368.
^ Borovik, Alexandre V.; Borovik, Anna (2010), "Exercise 14.4", Mirrors and Reflections, Universitext, New York: Springer, p. 109, doi:10.1007/978-0-387-79066-4, ISBN 978-0-387-79065-7, MR 2561378
^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
^ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
^ Weisstein, Eric W. "Truncated octahedral graph". MathWorld.

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3–9)
Freitas, Robert A. Jr. "Uniform space-filling using only truncated octahedra". Figure 5.5 of Nanomedicine, Volume I: Basic Capabilities, Landes Bioscience, Georgetown, TX, 1999. Retrieved 2006-09-08. {{cite web}}: External link in |publisher= (help)
Gaiha, P. & Guha, S.K. (1977). "Adjacent vertices on a permutohedron". SIAM Journal on Applied Mathematics. 32 (2): 323–327. doi:10.1137/0132025.
Hart, George W. "VRML model of truncated octahedron". Virtual Polyhedra: The Encyclopedia of Polyhedra. Retrieved 2006-09-08. {{cite web}}: External link in |publisher= (help)
Mäder, Roman. "The Uniform Polyhedra: Truncated Octahedron". Retrieved 2006-09-08.
Alexandrov, A.D. (1958). Konvexe Polyeder. Berlin: Springer. p. 539. ISBN 3-540-23158-7.
Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

External links

Weisstein, Eric W., "Truncated octahedron" ("Archimedean solid") at MathWorld.
- Weisstein, Eric W. "Truncated octahedral graph". MathWorld.
Weisstein, Eric W. "Permutohedron". MathWorld.
Klitzing, Richard. "3D convex uniform polyhedra x3x4o - toe".
Editable printable net of a truncated octahedron with interactive 3D view

[1] "Truncated Octahedron". Wolfram Mathworld.

[2] Doskey, Alex. "Adventures Among the Toroids – Chapter 5 – Simplest (R)(A)(Q)(T) Toroids of genus p=1". www.doskey.com.

[3] Perez-Gonzalez, F.; Balado, F.; Martin, J.R.H. (2003). "Performance analysis of existing and new methods for data hiding with known-host information in additive channels". IEEE Transactions on Signal Processing. 51 (4): 960–980. Bibcode:2003ITSP...51..960P. doi:10.1109/TSP.2003.809368.

[4] Borovik, Alexandre V.; Borovik, Anna (2010), "Exercise 14.4", Mirrors and Reflections, Universitext, New York: Springer, p. 109, doi:10.1007/978-0-387-79066-4, ISBN 978-0-387-79065-7, MR 2561378

[5] Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269

[6] Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

[7] Weisstein, Eric W. "Truncated octahedral graph". MathWorld.

[1]

[2]

[3]

[4]

[5]

[6]

[7]