Wikipedia:Reference desk/Archives/Science/2011 December 30
| Science desk | ||
|---|---|---|
| < December 29 | << Nov | December | Jan >> | December 31 > |
| Welcome to the Wikipedia Science Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
December 30
[edit]? on finding syndrome name
[edit]- The deletion can be seen here. Not to provide a diagnosis or anything, but "not being able to wear a wristwatch" is a common anecdote, but I can't find any actual studies on it. Though I could be wrong, I doubt you'd find any medical doctor to diagnose your condition, rural or otherwise. If you're looking for more information, of potentially dubious quality, you can just type "people who can't wear watches" into Google [1]. Buddy431 (talk) 05:45, 30 December 2011 (UTC)
- I can't wear a watch either (or, for that matter, glasses or any jewelry), but for different reasons. It does to my skin about what a cast does to anyone else's, turns it white and puffy. I had a pocket watch before cell phones came in, now I use that when I need to know the time. StuRat (talk) 05:53, 30 December 2011 (UTC)
Fractional Uncertainty with Zero Sloppiness
[edit]I'm trying to follow this and it starts out with a pool with the following measurements:
length L = 5.56 +/- 0.14 meters
= 5.56 m +/- 2.5%
I want to stop right there and note that the percentage having two significant figures makes sense since it would be calculated by ( 0.14 (2 sf) / 5.56 (3 sf) ) * 100% ( infinity sf)
width W = 3.12 +/- 0.08 meters
= 3.12 m +/- 2.6%
depth D = 2.94 +/m 0.11 meters
2.94 m +/- 3.7%
I think they got sloppy with the number of significant figures for the volume. Each of the length, width, and depth figures have 3 sfs, so the volume rounded to 3 sfs (let us suppose a round half to even convention in case we get a tie) is 51.0 m^3, but they put 51.00 m^3.
But that's not the thing that bothers me the most.
So the nominal measurements have 3 sfs, and the uncertainties have 2. As I already said, the fractional uncertainties should have 2 sfs. The convention they mention on that page is to add up the fractional uncertainties when measurements are multiplied or divided. Since a division was used to get fractional uncertainty, number of sfs was important, but now adding them, the lowest place value is what to look at. OK, adding 2.5% + 2.6% + 3.7% I get 8.8% which is kosher since each term is significant to the tenths place and so is the result. Now that we're about to multiply with that 8.8%, its number of sfs (2) should be what's important, right? Ignoring for a moment that they multiply their 51.00 * 8.8% (I would have multiplied it by 0.088, but I guess that's just notational), the bigger problem I see is that the uncertainty in volume should only have 2 sfs because the limiting figure was the 8.8% or 0.088 and not have an answer of 4.49 m^3 which has 3 (???) sfs (neither 4 like their nominal value nor 2 like their fractional uncertainty). I think the answer for nominal volume should be 51.0 m^3 with 3 sfs and volume uncertainty ought to be 51.0 m^3 * 0.088 = 4.5 m^3 with 2 sfs. This seems right because uncertainty is to the tenth of a cubic meter and the nominal volume is to the tenth of a cubic meter. Can anyone confirm they're wrong and I'm right or tell me why they're right, or what is right (with proof) if neither of us is? 69.243.220.115 (talk) 00:16, 30 December 2011 (UTC)
- Any use of significant figures is going to involve sloppiness. It can be a useful way of getting a rough and ready idea of the uncertainty in a number, but you are better off using the +/- numbers if they are known. If you don't want any sloppiness at all then don't convert the errors into percentages, keep them in the original form. --Tango (talk) 01:17, 30 December 2011 (UTC)
- If a professional engineer in the US as a member of ASME were given length 5.56 +/- 0.14 m, width 3.12 +/- 0.08 m, and depth 2.94 +/- 0.11 m, or a professional American physicist in the AIP were caring about this problem, and uncertainty in cubic meters were absolutely required (mentioning the original +/- numbers for each dimension were unacceptable, suppose the special concrete mix for the pool costs $100,000 per cubic meter, you only get one shot to pour it, and it's nonrefundable, nobody will buy your leftovers :) ), what would professional standards dictate is the correct answer? I know the problem at hand is with swimming pools, but with things like spacecraft and microchips, I doubt uncertainties are just considered 'rough and ready.' 69.243.220.115 (talk) 01:27, 30 December 2011 (UTC)
- See propagation of uncertainty for more details on this subject. The short answer is that there isn't an easy solution. You need to dig a little deeper into what those uncertainties really mean (ie. you need to know the probability distribution, or at least know whether it is reasonable to assume it is approximately normally distributed) and you need to know whether the uncertainties in the different measurements are connected at all (eg. if you underestimated the length, are you also likely to have underestimated the width?). If you have all of that information, then you can work it out. You can get some decent bounds on it using interval arithmetic, but that is only a little less rough and ready than significant figures. --Tango (talk) 03:15, 30 December 2011 (UTC)
- If a professional engineer in the US as a member of ASME were given length 5.56 +/- 0.14 m, width 3.12 +/- 0.08 m, and depth 2.94 +/- 0.11 m, or a professional American physicist in the AIP were caring about this problem, and uncertainty in cubic meters were absolutely required (mentioning the original +/- numbers for each dimension were unacceptable, suppose the special concrete mix for the pool costs $100,000 per cubic meter, you only get one shot to pour it, and it's nonrefundable, nobody will buy your leftovers :) ), what would professional standards dictate is the correct answer? I know the problem at hand is with swimming pools, but with things like spacecraft and microchips, I doubt uncertainties are just considered 'rough and ready.' 69.243.220.115 (talk) 01:27, 30 December 2011 (UTC)
- I agree with your criticism on excess significant figures, but we need to know what type of assumptions were made about the errors. If you are totally paranoid, and the errors are maximal rather than statistical, then the absolute maximum error is greater than 9% (range 55.632 to 46.629344 with unjustifiable accuracy!), but if the given errors are statistical then the maximum error in the volume is even greater, and the expected error smaller. We need to know the statistical model, as stated above. (The standard treatment assumes independent errors with a normal distribution.) You might be interested in this Wikipedia article: Experimental uncertainty analysis written by a retired nuclear scientist guy. Dbfirs 08:42, 30 December 2011 (UTC)
Pointed bullets
[edit]Why do guns fire blunt-nosed bullets instead of ones with sharp, pointed tips? Whoop whoop pull up Bitching Betty | Averted crashes 00:38, 30 December 2011 (UTC)
- Which guns and which bullets? There are all sorts of guns and all sorts of bullets, and they come in many shapes. --Jayron32 00:40, 30 December 2011 (UTC)
- Perhaps a little counter intuitively, in many cases a sharp pointed nose is not actually the most aerodynamically efficient design. We have an article Nose cone design which goes into some detail. Vespine (talk) 00:53, 30 December 2011 (UTC)
- See ballistics. Basically, the most streamlined shape for a supersonic projectile is one with a pointy nose, while the most streamlined shape for a subsonic projectile is one with a rounded nose. Beyond that, other nose shapes can be used for special purposes, such as armor-piercing bullets or hollow-point bullets. --Carnildo (talk) 00:54, 30 December 2011 (UTC)
- Bullet itself is also an interesting article on the subject. ←Baseball Bugs What's up, Doc? carrots→ 00:55, 30 December 2011 (UTC)
- In that case, since bullets travel at supersonic speed, wouldn't a sharp, pointed shape allow the bullet to travel fastest through the air and penetrate the deepest into flesh upon impact? Whoop whoop pull up Bitching Betty | Averted crashes 01:06, 30 December 2011 (UTC)
- Many military rifles do indeed fire a pointed bullet called a Spitzer; the name comes from the German for "pointy bullet". The US .30-06 Springfield, British .303 Mark VII, Russian 7.62×54mmR, 7.62×51mm NATO and 5.56×45mm NATO are all Spitzer shaped. Alansplodge (talk) 01:30, 30 December 2011 (UTC)
- In that case, since bullets travel at supersonic speed, wouldn't a sharp, pointed shape allow the bullet to travel fastest through the air and penetrate the deepest into flesh upon impact? Whoop whoop pull up Bitching Betty | Averted crashes 01:06, 30 December 2011 (UTC)
- Ballistics are more complicated than intuitive ideas about how things fly through the air. It's really complicated and you can be assured that very many very smart folks have spent a huge amount of time on it. The hollow-point article linked to earlier is particularly interesting from this point of view: in what seems paradoxical (if you don't understand ballistics), a concave design can cause the most flesh damage, because it expands inside of a target. Penetration of flesh is not that difficult to achieve, in and of itself, if you have a lot of energy behind whatever is flying through the air. Incidentally, if you make the projectile too pointy (e.g. as in a needlegun) it can pass right through the target, which is not as great (from a killing point of view) as expanding inside the target or bouncing around inside the target. --Mr.98 (talk) 01:35, 30 December 2011 (UTC)
- Some bullets travel at supersonic speed. Most handgun bullets and some rifle bullets travel at subsonic speeds. --Carnildo (talk) 02:40, 30 December 2011 (UTC)
- In that case, wouldn't the most efficient bullet design be one that changes shape based on what speed it's travelling at, so that it's pointed when it's travelling at supersonic speed, rounded when it's travelling at subsonic speed, and expanded when it's inside the target? Whoop whoop pull up Bitching Betty | Averted crashes 15:39, 30 December 2011 (UTC)
- That would not be very efficient from a cost point of view. Small arms ammunition is designed to be cheap, simple, lightweight, and reliable, for use by the so-called "line infantry" (... or at least, its modern equivalent). According to the BBC, 14 billion rounds of small arms ammunition are produced each year. Each cartridge, on average, costs much less than one dollar, to make up the $3 billion ammunition market. More advanced armaments exist, employing all sorts of sophisticated technologies; but not for the small arms market, where price and scale and portability are tantamount; individual performance is less important than average performance at scale. Nimur (talk) 16:46, 30 December 2011 (UTC)
- Bullets that expand or disintegrate inside the body were specifically banned by the Hague Convention of 1899. Alansplodge (talk) 18:03, 30 December 2011 (UTC)
- That would not be very efficient from a cost point of view. Small arms ammunition is designed to be cheap, simple, lightweight, and reliable, for use by the so-called "line infantry" (... or at least, its modern equivalent). According to the BBC, 14 billion rounds of small arms ammunition are produced each year. Each cartridge, on average, costs much less than one dollar, to make up the $3 billion ammunition market. More advanced armaments exist, employing all sorts of sophisticated technologies; but not for the small arms market, where price and scale and portability are tantamount; individual performance is less important than average performance at scale. Nimur (talk) 16:46, 30 December 2011 (UTC)
- In that case, wouldn't the most efficient bullet design be one that changes shape based on what speed it's travelling at, so that it's pointed when it's travelling at supersonic speed, rounded when it's travelling at subsonic speed, and expanded when it's inside the target? Whoop whoop pull up Bitching Betty | Averted crashes 15:39, 30 December 2011 (UTC)
- It is an often repeated myth that Expanding bullets are banned per se. Just look at what your friendly local cops carry around.--Aspro (talk) 19:26, 30 December 2011 (UTC)
- They're banned in warfare under the Hague Convention. Neither Hague nor Geneva apply to domestic situations.
- ALR (talk) 10:36, 31 December 2011 (UTC)
- It is an often repeated myth that Expanding bullets are banned per se. Just look at what your friendly local cops carry around.--Aspro (talk) 19:26, 30 December 2011 (UTC)
- That’s what my last post put into context; for the benefit of the OP.--Aspro (talk) 18:12, 31 December 2011 (UTC)
Oddly strong magnetic force
[edit]I was installing a new hardrive in my PC the other day when I felt a resistance in my hand as I brought the new drive toward the case. It was at least a foot away at the time so I thought I must have imagined it. Waving the drive through the air several times I descovered a couple of "pockets" of resistance in the air, one of these was at least two feet away from the case, the other hard drives or any other metal object that it could possibly have been interacting with.. are these rare earth magnets realy so strong? I have never expereinced this before, and I've often stacked drives far closer to eachother. e.g. on top of eachother on a shelf and even at such close proximity never felt any such magnetic interaction.. could it be an abnormally strong magnet in this new drive, and could it adversely affect nearby devices? Benjamint 03:25, 30 December 2011 (UTC)
- I doubt it would be the magnet. Was the drive plugged in at the time? I suspect you might have felt the centrifugal force of the spinning platters, that can be strange and feel quite "strong" if you haven't felt it before. I can imagine how you could mistake it for appearing only in "pockets" since you only feel it if you move the drive in a particular way. Vespine (talk) 04:05, 30 December 2011 (UTC)
- I'd recommend a little experiment: Bring the old HD to a place away from other metals. Move a compass around it at some convenient distance and note down the maximum change of the needle, and the distance. Repeat the same with the new HD. If the numbers are significantly different then we have something quantitative to discuss here. — Sebastian 04:16, 30 December 2011 (UTC)
- I've taken a number of old HDDs apart, and from my experience with the magnets, their field (as far as it can be felt by hand when they're brought closer together) extends a few centimetres. A few feet is completely the wrong scale. For a fun look at the topic, see Daniel Rutter's article for quotes like:
--Slashme (talk) 05:55, 30 December 2011 (UTC)You're not going to be lifting any Toyotas with a five buck magnet from anywhere. Nails will hop up only about an inch to hit the strongest of the magnets in the ForceField grab bags. In contrast, ferromagnetic objects of all types will fly across a room to make friends with an MRI machine, as occasional accidents attest.
- centrifugal force sounds plausible, i should have thought of that. Benjamint 08:49, 30 December 2011 (UTC)
- It's actually the Coriolis effect, not a centrifugal force. It is very noticeable with a gyroscope, and is probably detectable from a fast-spinning hard drive. Dbfirs 14:18, 31 December 2011 (UTC)
- You are probably right that it's not technically centrifugal force, but I am not convinced that it is Coriolis either, the examples given in the article do not resemble the gyroscopic effect I'm trying to describe at all. And none of the articles about gyroscopes mention Coriolis. I think most people would understand what is meant by centrifugal, even if it is not the correct term. I actually still can't find the correct term.. Looking for gyroscope and coriolis i found this article which describes the effect in ballistics, calling it gyroscopic spin drift, but even after finding the wiki section it doesn't specify what the causal effect is called. Vespine (talk) 23:11, 2 January 2012 (UTC)
- Both "centrifugal" and "Coriolis" "forces" usually refer to fictitious forces "observed" in a rotating frame of reference, so that wouldn't apply here. Perhaps "gyroscopic effect" would be a better description, but we don't have an article. Dbfirs 00:21, 3 January 2012 (UTC)
- You are probably right that it's not technically centrifugal force, but I am not convinced that it is Coriolis either, the examples given in the article do not resemble the gyroscopic effect I'm trying to describe at all. And none of the articles about gyroscopes mention Coriolis. I think most people would understand what is meant by centrifugal, even if it is not the correct term. I actually still can't find the correct term.. Looking for gyroscope and coriolis i found this article which describes the effect in ballistics, calling it gyroscopic spin drift, but even after finding the wiki section it doesn't specify what the causal effect is called. Vespine (talk) 23:11, 2 January 2012 (UTC)
Maximum sustained G-force a human can endure for long periods?
[edit]Suppose a human live in a space station attached to a rocket that accelerate for long periods (weeks) to have to deal with eat, sleep, control tasks etc. What is the maximum acceleration that can be sustained continuously before the human body won't work properly? Like being unable to digest food, breathe, overload heart etc. Electron9 (talk) 08:43, 30 December 2011 (UTC)
- Keep in mind that acceleration is change in speed over time. I have trouble imagining that a space station would be continuously increasing its speed over a period of weeks. As far as how much G-force a human can handle, rocket sled might have some answers. Also g-force. ←Baseball Bugs What's up, Doc? carrots→ 09:53, 30 December 2011 (UTC)
- I wouldn't call such a thing a space station, but it is plausible that an interstellar spacecraft might do something like that. There are existing and planned spacecraft for travelling within the solar system using ion drives that accelerate for long periods, although their acceleration is much less than 1g. You could have a similar system for interstellar travel where you accelerate at more than 1g (although we don't have the technology to do that yet). 2g for a week gets you to 4% the speed of light, which is the kind of speeds you need to achieve to make interstellar travel feasible (examples of reaching higher speeds would require me to take into account special relativity, which I don't feel like doing - I expect you can find online calculators with some simple googling, just be careful about what reference frame the acceleration is measured in). --Tango (talk) 14:32, 30 December 2011 (UTC)
- 4% of the speed of light hardly seems practical for interstellar travel. At that speed it would take over 100 years to get to the nearest star, and chances are a faster ship launched later would pass you on the way (pointing and laughing as they pass). StuRat (talk) 16:30, 30 December 2011 (UTC)
- True, but it's also about the limit of what you can calculate without taking special relativity into account. If you can maintain 2g for a week, you can probably maintain it for a month without too much extra difficulty (your fuel requirements would increase exponentially if you were using a traditional rocket, but you probably couldn't manage a week with that kind of approach anyway), by which time you are getting up to speeds where travelling between stars within a human lifespan is possible. Getting up to speeds where you aren't likely to be overtaken by the next generation of craft is an interesting issue and not one that is easy to figure out. Once you reach large proportions of the speed of light, you are pretty safe, though. --Tango (talk) 20:31, 31 December 2011 (UTC)
- And then there's the issue that nobody wants to fund a project, knowing it will likely be overtaken by faster craft on the way. But, on the other hand, if nobody funds the first project, the knowledge base will not exist to build the faster ships, later. And we can't develop near-light-speed travel for zipping around our solar system, and then apply that the interstellar travel, as the G's would kill us on the short trips. Quite the Catch-22. This somewhat reminds me of the issue of subsonic versus supersonic commercial airplanes. Supersonic seems to make sense for long trips, but such planes are lousy at shorter, subsonic flights, so developing a fleet of SST's is impractical, dooming us all to long subsonic flights. StuRat (talk) 22:11, 31 December 2011 (UTC)
- We have an article on this subject (of course): Space travel using constant acceleration. --Tango (talk) 14:33, 30 December 2011 (UTC)
- That article has kind of a conversational tone that suggests it was lifted from elsewhere. Be that as it may, if I'm understanding correctly, the problem with a high g-force has to do with "pushing" against a gravitational field. But if you're in deep space, you wouldn't have that problem, would you? ←Baseball Bugs What's up, Doc? carrots→ 15:33, 30 December 2011 (UTC)
- To redeploy a famous quote: Bugs, you're not even wrong. {The poster formerly known as 87.81.230.195} 90.197.66.116 (talk) 15:57, 30 December 2011 (UTC)
- I would expect that we can't handle more than 1.1 or 1.2 g for any extended time period. Perhaps with special equipment, like a pressure suit that compresses and relaxes to help pump the blood, we might be able to do slightly more. The work load a person can handle would also be reduced, as just walking around would be exhausting. Instead of sitting (on the relatively small buttocks), people would need to recline on their backs, as astronauts to in launch position, to distribute the force over a wider area. Special shoes and/or floor coverings would also be needed, to reduce the stress on the feet while walking, and to protect them from falling objects. StuRat (talk) 16:27, 30 December 2011 (UTC)
- Do you have any references to support your statements, StuRat, or is that just speculation? (And if speculation, do you have any professional or educational experience or qualifications that might qualify you to offer such guesses?) TenOfAllTrades(talk) 17:27, 30 December 2011 (UTC)
- To paraphrase your previous comment to me, you've wasted my time more than enough already. You're over your quota, and I have no intention of getting into a debate with someone as rude as you. StuRat (talk) 03:18, 31 December 2011 (UTC)
- That's "no", then? TenOfAllTrades(talk) 03:24, 31 December 2011 (UTC)
- It's "no intention of taking the bait", go stalk somebody else. StuRat (talk) 03:33, 31 December 2011 (UTC)
- I have no idea what this is all about, but I'd also like to see corroboration of the 1.1 - 1.2 g figure. A high-g environment is not like obesity in many ways: obese bodies have adapted to their new weight, but obesity is also harmful for reasons other than the increased weight itself. For example, I think cardiovascular problems, higher risk of cancer, and higher risk of diabetes are more due to the poor diet and sedentary lifestyle than due to gravity. The question of what happens to the human body under increased gravity, but without the diet and lifestyle associated with obesity, is an interesting question that I'm not sure any research addresses. --99.237.252.228 (talk) 08:29, 31 December 2011 (UTC)
- I believe that the need to pump more blood through more tissue is a large factor in cardiovascular disease. This requires greater blood pressure variations to distribute the blood, which causes damage. On cancer and diabetes you may well be right, though. A better analogy might be giants, of normal weight for their height. I believe they do suffer health consequences as a result of their size, even with a healthy diet.
- Ten likes to stalk me and post comments like that. If I then posted a list of qualifications, he would dismiss anything less than a Nobel prize in that area as insufficient. You will notice he posted no qualifications while demanding mine. And, he has posted nothing helpful towards answering your questions. So, I ignore him. StuRat (talk) 20:17, 31 December 2011 (UTC)
- My qualifications (or references that I might provide) would be relevant if I were offering a different answer, or asserting that StuRat's response was definitely incorrect. On the other hand, it doesn't take specialized skills to notice that his response contained no references supporting his claimed answer. Irrelevant obfuscation about Nobel laureates notwithstanding, it appears that in addition to not basing his response on any real research that he did, he also lacks any specific medical or aeronautical training that might qualify him to offer a professional expert opinion. In other words, he's mad that someone noticed that he posted a response (probably an incorrect one, based on the replies below from editors who actually did bother to find real sources) that he made up out of whole cloth, and that he got called on it. I have called him on such answers before; he has a habit of offering authoritative-sounding responses that aren't based in any real research or knowledge, and he doesn't seem to realize that his idle speculation at our Reference Desk is harmful. TenOfAllTrades(talk) 21:13, 31 December 2011 (UTC)
- Based on StuRat's response to my query, it appears that the 1.1-1.2g figure is something he made up without doing any research at all; it's probably best to ignore it. TenOfAllTrades(talk) 19:32, 31 December 2011 (UTC)
- StuRat's 1.1 or 1.2 g limit seems overly pessimistic. A patient who is class I obese (BMI 30.0–34.9) weighs up to 1.89 times as much as their "normal weight" (BMI 18.5–24.9). -- 49.229.138.140 (talk) 17:33, 30 December 2011 (UTC)
- So how high can BMI go from normal to obese for a long period without destroying the joints etc? Electron9 (talk) 20:53, 30 December 2011 (UTC)
- I can only note that while osteoarthritis is an issue with the obese, type 2 diabetes mellitus and cardiac problems (from DVI to MI) seem to be more serious, and it is not clear how far the high-g vs. obesity comparison would hold. Most issues with obesity are due to physiological effects well beyond just the weight of the excess tissue, while high-g would introduce a head-to-tow blood pressure variation not present in obesity. (prev. posted as 49.229.138.140 ) -- 110.49.224.36 (talk) 02:44, 31 December 2011 (UTC)
- Note that the bodies of the obese have made various adjustments to carry their weight, as they gained it, such as increased muscle mass. I was assuming no such adjustments were made by the astronauts ahead of time, but perhaps you could have them live in a centrifuge or wear weights to bulk up for such an experience. The obese also suffer health problems and can't do as much activity, so are we saying it's OK to damage the health of the astronauts and have them be less productive ? StuRat (talk) 03:07, 31 December 2011 (UTC)
- A report from The Ohio state university on page 11, figure 6 hints that 4G is the maximum for period of 25 seconds, and the diagram suggest it can be sustained. If digestion, lungs, blood system, judgement etc will work for weeks in 4G is another matter ;) Electron9 (talk) 17:11, 30 December 2011 (UTC)
- They said that if 4G can be maintained for 25 seconds they can conclude from that it's fine indefinitely ? That's quite an extrapolation. StuRat (talk) 21:26, 31 December 2011 (UTC)
- Assuming high-g constant acceleration space travel is possible (given all its technical problems), accelerating at over 1 g does not buy you much in terms of total travel time for interstellar trips, though it does reduce the subjective time for the travelers. If we can trust the relativistic calculations done by this space math calculator, a 20 light-year trip at 1 g (half accelerating, half decellerating) would take 21.87 years (6.05 years subjective time), while at 10 g it would take 20.21 years (1.04 years subjective time). So it would seem that human adaptability to long term high-g environments would be less a factor in determining appropriate transportation than in deciding what constitutes a habitable planet. (I see that article discusses habitability for life in general, not humans specifically.) -- 110.49.224.36 (talk) 03:21, 31 December 2011 (UTC)
- That calculator seems a bit iffy. When I used low enough accels and distances to avoid relativistic effects, the numbers didn't seem to match Newtonian math. StuRat (talk) 03:31, 31 December 2011 (UTC)
- Is it a display issue? If you feed the "Long Relativistic Journeys" (acel/decel) calculator with a = 1 g & d = 980.665 m, it appears to claim that t = 6.342 years, but if you scroll within that result box, you see 6.342000000000084e-7 years, or 20 seconds. (10 seconds accelerating for the first 490.3325 m, 10 seconds decelerating for the second 490.3325 m.) -- 110.49.224.96 (talk) 07:21, 31 December 2011 (UTC)
- Yes, that may be the problem. StuRat (talk) 20:05, 31 December 2011 (UTC)
- 110.49: the calculations look correct, because the spaceship would be travelling at nearly light speed under even 1g acceleration, but how did you arrive at the conclusion that "human adaptability to long term high-g environments is less a factor"? If you're on the spaceship, it would make a big difference if you arrive in 1.04 years or 6.05 years. I, for one, would sign up for the 1-year trip if I can survive it, but would go insane if I was stuck on a ship for 6 years! Also, you'd need 6 times as much food, water, air, games to kill boredom, and the like at 1g than at 10g. For people on Earth or at the destination planet, the difference between 21.87 and 20.21 years is insignificant, so the only consideration is really the subjective time felt by the astronauts. --99.237.252.228 (talk) 08:48, 31 December 2011 (UTC)
- At 10g you won't be playing any games, unless you consider "try to keep from passing out" a game. :-) StuRat (talk) 20:05, 31 December 2011 (UTC)
- You are right; I shouldn't have dismissed the importance of the subjective travel time. In this particular case, however, I'd rather risk six years of potentially going insane than one year of going squish. -- (110.49.224.96 finally logged in) ToE 10:14, 31 December 2011 (UTC)
- Poul Anderson's Tau Zero is the best science fiction example of a one g constant acceleration trip set in a universe without FTL drive. For higher-g, long duration accelerations, the only example which comes to mind is Robert A. Heinlein's juvenile Have Space Suit—Will Travel, in which the narrator is kidnapped by an alien "Wormface" and whisked off to Pluto at 8 g. Heinlein steps us through our hero's calculations in his lonly Plutonian cell, where he determines that the trip took five and a half days at 8 g. He is then quite surprised to realize that it would only have taken fifteen days at 1 g. "It seemed to me that it ought to take at least eight times as long at one gee as at eight — more likely sixty-four." He then realizes why t is scaling inversely to the square root of a in s = 1/2 a t2, "... because the more boost, the shorter the trip, and the shorter the trip the less time in which to use the built-up speed." Back to the OP's question, the protagonist was unconscious for most of the trip due to the effects of the acceleration. In the words of "Fats", one of Wormface's henchmen, "Five days at eight gravities ain't no joy ride." -- ToE 10:14, 31 December 2011 (UTC)
- Also relevant is our article Liquid breathing#Space travel. -- ToE 10:29, 31 December 2011 (UTC)
- Also ECMO with liquid immersion (and cavity filling) with a non-oxygen carrying liquid, overcoming the density issues with Perfluorocarbon fluids. -- ToE 10:44, 31 December 2011 (UTC)
I suspect that by gradually increasing the g-load over a period of months or even a few years, you can let physically fit people adapt to living permanently at a few g's. In case of low oxygen, you can actually adapt to live permanently at levels that will make you pass out within minutes if oxygen levels were lowered immediately to that level. Another example: if you increase your fitness by exercising for longer and at higher intensisty, you will likely reach a point where forced exercise at that level before you started to exercise using e.g. amphetamines to overrule your bodies defenses against over exertion, would have been fatal. So, the daily routine of physically fit people is already well within the death zone of the same persons in an unfit couch potato state (but note that Wikipedia calls this latter state the norm, while calling the fit state a diseased state, see the athletic heart syndrome article). The g-load that will kill you within minites is quite large, the g-force that will make you pass out is typically somehwere between 3 and 8 g's, so you could speculate that such large g-loads that would incapacitate you within minutes or even kill you, could actually be sustainable on the long. Then a much more conservative guess would be that g-loads below 3 g's that typically don't incapacitate you immediately could be survivable on the long run, if you give your body the necessary time to adapt to it. Count Iblis (talk) 01:26, 1 January 2012 (UTC)
- One factor to consider is that it might be quite difficult to sleep at high g's. Your system couldn't "relax", because it needs to keep beating your heart quickly to distribute your blood. And you'd need to constantly shift positions to avoid pressure sores (although a special bed might avoid that or turn you continuously). So, sleep deprivation could become an issue. StuRat (talk) 03:44, 2 January 2012 (UTC)
Would any surgeries or maybe nanotechnology or bioengineering be imaginable to make us more resilient to high g travel? Bastard Soap (talk) 17:28, 2 January 2012 (UTC)
Wouldn't full body immersion solve most of these issues? Greglocock (talk) 21:05, 2 January 2012 (UTC)
What'll it take to upgrade landline networks to allow texting to and from landline phones?
[edit]Best Buy keeps telling me that none of their landline phone models for sale have texting capabilities.
I'm afraid that I've vowed never to own my own landline until texting capabilities arrive to them.
What will it take to give landlines the capability to send and receive texts? Thanks. --70.179.174.101 (talk) 09:17, 30 December 2011 (UTC)
- I'm not sure where you live, but that's been available in Australia since at least 2005 - see this article about the national provider Telstra introducing the service. It even talks about it being available on public payphones. I can't say about elsewhere in the world, but I'd be pretty sure this wasn't invented in Aust. --jjron (talk) 11:07, 30 December 2011 (UTC)
- I remember this being offered I believe before 2005 in Malaysia. ([2] suggests it was 2004 although I thought it was before then.) Of course the key point Jjron touched on, it obviously depends on your telco more then your phone. If they don't already have it, I have some doubts it will be added to POTS landlines particularly in a place like the US. Digital ones over cable, DSL, fibre etc is already supported by some providers. I presume some VoIP phones support SMS but I'm not aware and a search doesn't suggest there's any real standard for SMS over Session Initiation Protocol or some other standard way for the VoIP hard phones to receive and send SMS. On the other hand, it's not clear to me why the OP wants SMS over their 'landline' anyway. Nil Einne (talk) 11:42, 30 December 2011 (UTC)
- Which country? For textable landlines in the UK, see here for example.--Shantavira|feed me 12:33, 30 December 2011 (UTC)
- Quickfix, use a modem. The other way is to replace the line card at the telephone exchange with that that can handle this function. Otoh, maybe ISDN can be made to deal with this using it's 9600 bit/s control line. Electron9 (talk) 16:54, 30 December 2011 (UTC)
- A fax machine of sorts has been able to this for over 145 years. If you mean texting in the same sense as a mobile phone would work, BT in the UK has provided that service for their home customers for the last few years. That suggests it is a feature provided by the telephone network that you should be looking for first. Astronaut (talk) 02:19, 31 December 2011 (UTC)
- By the way, the IP geolocates to Auburn in metro Topeka, Kansas. Nyttend (talk) 05:28, 31 December 2011 (UTC)
- Your question seems confusing to me: what do you need? a landline phone with texting or a landline with texting? Lanlines phones with texting seems to be pretty uncommon, but texting through the landline network is hardy new news. 88.8.75.198 (talk) 19:41, 31 December 2011 (UTC)
"Formaldehyde appears to be a useful probe for astrochemists due to its low reactivity in the gas phase and to the fact that the 110←111 and 211←212 K-doublet transitions are rather clear."
What is the 110←111 and 211←212?Curb Chain (talk) 09:57, 30 December 2011 (UTC)
- (ec) They are spectral lines - characteristic colors of light that formaldehyde molecules emit when heated. They are described in this section of the article: 6.2 cm and 2.1 cm electromagnetic waves - in other words, on the low end of the microwave spectrum (or high end of the UHF band). We have an article on radio astronomy to give you some background, and you may also want to read emission spectrum if you're unfamiliar with the basics of chemical spectroscopy. Nimur (talk) 17:08, 30 December 2011 (UTC)
- Follow the link to the article on Interstellar formaldehyde which explains it - and contains further links to explain ground state and rotational transition. Rmhermen (talk) 17:07, 30 December 2011 (UTC)
- Both articles don't mention the notation though. If Interstellar formaldehyde explains this, it doesn't explain the formulae for notation/nomenclature.Curb Chain (talk) 03:12, 31 December 2011 (UTC)
Cross-Coupled Oscillator Driving Induction Heater
[edit]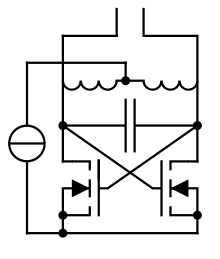
I've been thinking of building an induction heater for a while now, but there's something bothering me.. Most people build an LC tank circuit with the induction coil and some capacitors and drive it with powerful transistors. To tune in to the right frequency a separate circuit is used. Example 1: http://hildstrom.com/projects/inductionfoundry/index.html Example 2: http://www.mindchallenger.com/inductionheater/ The burning question is: why not use a cross-coupled LC oscillator (or similar oscillator) with the coil as the inductive heater coil?! It will naturally resonate at the right frequency and powerful MOSFETs can keep it operating at high powers! Any ideas? Duga3 (talk) 17:58, 30 December 2011 (UTC)
Self tuned invertors for this application are a bad idea - especially if you are inexperienced. A separate frequency determining drive circuit gives you independent and therefore greater control over a multitude of circuit parameters. Also, don't forget that you'll have a sine wave across the tank, but the MOSFET currents for this must be narrow pulses "pumping" each sine peak, or you'll waste most of the power in the MOSFETs and not in the load/workpiece. Pulse width is easily predicted and controlled with a separate oscillator drive, but difficult and probably impossible with simple self oscillating circuits unless the MOSFET gate ratings are exceeded. Looking at it another way, you should be driving the MOSTFET gates with rectangular pulses, but simple cross coupling drives the gates with sine waves - not only does this directly lead to poor efficiency, it also leaves the MOSFETS open to parasitic oscillation at very high and useless frequencies. I have designed self-oscillating invertors using PNP transistors, so they can be made to work, but I would not try it for this application. They do have a theoretical advantage in that a short circuit load or gross overload should stop oscillation - but in practice heavy loads still write off the transistors. — Preceding unsigned comment added by 124.182.5.136 (talk) 10:00, 31 December 2011 (UTC)
- That does makes sense, thanks for your help. Duga3 (talk) 01:19, 5 January 2012 (UTC)
How far away could Seti detect us?
[edit]Say there's an alien civilization basically identical to ours, with the same amount of radiowave output. How close would that civilization have to be in order for SETI to pick it up? (I suspect a spectrum of distances, from definitive to... less definitive). Goodbye Galaxy (talk) 19:32, 30 December 2011 (UTC)
- I'm not sure of the answer (not an expert), but you may be interested in Active SETI, which covers this. Meelar (talk) 19:54, 30 December 2011 (UTC)
- And on a semi-related note, here's an article about building a beacon to signal interstellar civilizations. Astronomy Now link. Meelar (talk) 20:04, 30 December 2011 (UTC)
- Depending on your "us", the distance is surprisingly short. IIRC, the Arecibo Observatory could detect Earth's general non-directional radio emissions at a distance of no more than a light-year or two. On the other hand, Arecibo is also a powerful directional radio transmitter (it's been used for radar surveys of the solar system), and could detect itself at a fairly long distance (I've heard 30 light-years and 1000 light-years, but can't find references for either). --Carnildo (talk) 01:18, 31 December 2011 (UTC)
- Update: According to this page, the Arecibo antenna could detect the Arecibo Message "just about anywhere in the galaxy", for a distance of around 100,000 light-years. --Carnildo (talk) 01:24, 31 December 2011 (UTC)

- This question is such a natural one that I am amazed I've never seen it fully addressed; you'd think it would be mentioned in every SETI discussion. The detection range will, of course, be much greater for directed signals, as with Active SETI. Last month, the WP:RD/S question "Radio distance" asked about the effective range of interstellar communication. Based on the 10 TW EIRP of Arecibo Observatory's 2380 MHz signal, this 1981 reception range chart, and subsequent receiver sensitivity improvements suggested by numbers given in the section SETI#MOP and Project Phoenix, I estimated that the Arecibo message could conceivably be detected by an equivalent civilization at its target some 25,000 light years away (assuming they will be listening in just the right distance at just the right time).
- Active SETI aside, military radars can be quite powerful and well focused. NAVSPASUR's Lake Kickapoo master transmitter puts out 768 kW of 216.983 MHz CW, with an EIRP of 6.3 GW suggested on some discussion boards (couldn't find an RS). (Any complete discussion should also mention the detection range of our isotropic transmissions (including the 1936 Berlin Olympics transmission mentioned in Contact.) -- ToE 02:03, 31 December 2011 (UTC)
- On practical maximum distance is N light-years, where N is the number of years for which we have been transmitting radio waves - currently about 125. Any further away than that our radio signals haven't reached yet, so we can't be detected, no matter how sensitive/powerful the receiver. Obviously this maximum distance increases at the rate of 1 light-year per year. Mitch Ames (talk) 02:22, 31 December 2011 (UTC)
- Yes, but I don't think the OP is actually interested in detecting humanity, but in detecting other humanity-like civilisations. If such a civilisation is 500 ly away and reached our level of technology 500 years ago, then whether or not we can detect them will depend on whether or not we could detect us at a distance of 500 ly. --Tango (talk) 20:24, 31 December 2011 (UTC)
- say that this civilisation was 30 years ahead or behind us technologically wise-that could change everything. the chances of it being exactly at the same point technologically is tiny. — Preceding unsigned comment added by 109.152.106.203 (talk • contribs) 20:58, 2 January 2012 (UTC)
Beyond the speed of light
[edit]Could there be something like "speed of space", since basically the universe is space in constant expansion and photons can't be present at distances greater than 13.7 billion light years at any given point? Gravitoweak (talk) 23:43, 30 December 2011 (UTC)
- I'm not sure I follow you, but the article Hubble's law may have some reading which may interest you. --Jayron32 23:52, 30 December 2011 (UTC)
- We do have the articles metric expansion of space and cosmic inflation. Are you asking what units this expansion is measured in? -- 110.49.224.36 (talk) 03:30, 31 December 2011 (UTC)
