Wikipedia:Reference desk/Mathematics: Difference between revisions
Fly by Night (talk | contribs) →Simple Set Theory: {{resolved}}, {{archive}}, thanks everyone. |
|||
| Line 218: | Line 218: | ||
== Simple Set Theory == |
== Simple Set Theory == |
||
{{archivetop}} |
|||
{{resolved}} |
|||
[[Image:Venn 0110 1001.svg|thumb|<center>A [[Venn Diagram]] showing the relationship</center>]] |
[[Image:Venn 0110 1001.svg|thumb|<center>A [[Venn Diagram]] showing the relationship</center>]] |
||
I know that we're lucky to have many talented set theorists on this page, so I'm sure my question will be answered in no time. Given a set ''X'', take two [[subset]]s, say ''A'' and ''B'', and consider the [[union (set theory)|union]] {{nowrap|1=''A'' ∪ ''B''}} and the [[intersection (set theory)|intersection]] {{nowrap|''A'' ∩ ''B''}}. For a set {{nowrap|1=''C'' ⊆ ''A''}}, let {{nowrap|1=''A'' − ''C'' = {''a'' ∈ ''A'' : ''a'' ∉ ''C''}}}. Let P(''X'') denote the [[power set]] of ''X''. Define a [[binary operation]] {{nowrap|1=ƒ : P(''X'') × P(''X'') → P(''X'')}} given by {{nowrap|1=ƒ(''A'',''B'') = (''A'' ∪ ''B'') − (''A'' ∩ ''B'').}} Notice that this is well defined since {{nowrap|1=''A'' ∩ ''B'' ⊆ ''A'' ∪ ''B''}}. Let us write ''A''⋅''B'' in place of ƒ(''A'',''B''). I want to show that this binary operation is [[associative]], i.e. for any subsets, ''A'', ''B'' and ''C'', of the set ''X'' we have {{nowrap|1=(''A''⋅''B'')⋅''C'' = ''A''⋅(''B''⋅''C'')}}. Explicitly this associativity condition becomes: |
I know that we're lucky to have many talented set theorists on this page, so I'm sure my question will be answered in no time. Given a set ''X'', take two [[subset]]s, say ''A'' and ''B'', and consider the [[union (set theory)|union]] {{nowrap|1=''A'' ∪ ''B''}} and the [[intersection (set theory)|intersection]] {{nowrap|''A'' ∩ ''B''}}. For a set {{nowrap|1=''C'' ⊆ ''A''}}, let {{nowrap|1=''A'' − ''C'' = {''a'' ∈ ''A'' : ''a'' ∉ ''C''}}}. Let P(''X'') denote the [[power set]] of ''X''. Define a [[binary operation]] {{nowrap|1=ƒ : P(''X'') × P(''X'') → P(''X'')}} given by {{nowrap|1=ƒ(''A'',''B'') = (''A'' ∪ ''B'') − (''A'' ∩ ''B'').}} Notice that this is well defined since {{nowrap|1=''A'' ∩ ''B'' ⊆ ''A'' ∪ ''B''}}. Let us write ''A''⋅''B'' in place of ƒ(''A'',''B''). I want to show that this binary operation is [[associative]], i.e. for any subsets, ''A'', ''B'' and ''C'', of the set ''X'' we have {{nowrap|1=(''A''⋅''B'')⋅''C'' = ''A''⋅(''B''⋅''C'')}}. Explicitly this associativity condition becomes: |
||
| Line 235: | Line 237: | ||
::::::::I very much doubt that you will be able to "''identify the group''". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to ''learn something new''. Better that we leave it here, Tango. Thanks all the same. <span style="white-space:nowrap;">— [[User:Fly by Night|<span style="font-family:Segoe print">'''''Fly by Night'''''</span>]] <font color="#000000">([[User talk:Fly by Night|<span style="font-family:Segoe print">talk</span>]])</font></span> 00:12, 9 August 2010 (UTC) |
::::::::I very much doubt that you will be able to "''identify the group''". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to ''learn something new''. Better that we leave it here, Tango. Thanks all the same. <span style="white-space:nowrap;">— [[User:Fly by Night|<span style="font-family:Segoe print">'''''Fly by Night'''''</span>]] <font color="#000000">([[User talk:Fly by Night|<span style="font-family:Segoe print">talk</span>]])</font></span> 00:12, 9 August 2010 (UTC) |
||
:::::::::Algebraist ''has'' identified the group (see below): it's <math>\Z_2^{|X|}</math>. --[[User:Tango|Tango]] ([[User talk:Tango|talk]]) 00:27, 9 August 2010 (UTC) |
:::::::::Algebraist ''has'' identified the group (see below): it's <math>\Z_2^{|X|}</math>. --[[User:Tango|Tango]] ([[User talk:Tango|talk]]) 00:27, 9 August 2010 (UTC) |
||
::::::::::Exactly: ''Algebraist'' has identified the group. You were talking about finite groups when I had general topologies in mind. That's why I got a frustrated. I apologise for letting things annoy me so easily. <span style="white-space:nowrap;">— [[User:Fly by Night|<span style="font-family:Segoe print">'''''Fly by Night'''''</span>]] <font color="#000000">([[User talk:Fly by Night|<span style="font-family:Segoe print">talk</span>]])</font></span> 22:25, 9 August 2010 (UTC) |
|||
::::There is an obvious isomorphism between P(''X'') and the direct product of |X| copies of '''Z'''<sub>2</sub>: just replace sets with their indicator functions, as Trovatore suggested. [[User talk:Algebraist|Algebraist]] 22:52, 8 August 2010 (UTC) |
::::There is an obvious isomorphism between P(''X'') and the direct product of |X| copies of '''Z'''<sub>2</sub>: just replace sets with their indicator functions, as Trovatore suggested. [[User talk:Algebraist|Algebraist]] 22:52, 8 August 2010 (UTC) |
||
| Line 244: | Line 247: | ||
::::::::I know. I am referencing a comment from above by Fly By Night who told Tango he didn't need to point out anything that was clearly true. [[User:StatisticsMan|StatisticsMan]] ([[User talk:StatisticsMan|talk]]) 16:35, 9 August 2010 (UTC) |
::::::::I know. I am referencing a comment from above by Fly By Night who told Tango he didn't need to point out anything that was clearly true. [[User:StatisticsMan|StatisticsMan]] ([[User talk:StatisticsMan|talk]]) 16:35, 9 August 2010 (UTC) |
||
Thanks to everyone for their answers. I now consider my question to be resolved. Thanks to Trovatore, Tango and Algebraist for their, as ever, insightful comments. I'm also going to archive the thread because I don't think it's moving in such a positive direction. Seeing as the question has been resolved in the OP's eyes, I don't see any problem in archiving. Thanks again to everyone. <span style="white-space:nowrap;">— [[User:Fly by Night|<span style="font-family:Segoe print">'''''Fly by Night'''''</span>]] <font color="#000000">([[User talk:Fly by Night|<span style="font-family:Segoe print">talk</span>]])</font></span> 22:25, 9 August 2010 (UTC) |
|||
{{archivebottom}} |
|||
= August 9 = |
= August 9 = |
||
Revision as of 22:25, 9 August 2010
of the Wikipedia reference desk.
Main page: Help searching Wikipedia
How can I get my question answered?
- Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
- Post your question to only one section, providing a short header that gives the topic of your question.
- Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
- Don't post personal contact information – it will be removed. Any answers will be provided here.
- Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
- Note:
- We don't answer (and may remove) questions that require medical diagnosis or legal advice.
- We don't answer requests for opinions, predictions or debate.
- We don't do your homework for you, though we'll help you past the stuck point.
- We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.
How do I answer a question?
Main page: Wikipedia:Reference desk/Guidelines
- The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.
August 3
The Stone-Cech Compactification of a topological space
Hi, I am trying to figure out the topology on that space. If I understand correctly' the clopen sets in this topology are A={F | A is in F}. My question is this: suppose that a point x is in A in the original topology of the space X. Does the clopen set A we defined on the Stone-Cech Compactification perform an open neighborhood for the principal filter of x? Is this the idea of this compactification? And if so, then what is the meaning of convergence in this space? Thanx! —Preceding unsigned comment added by Topologia clalit (talk • contribs) 09:13, 3 August 2010 (UTC)
- I presume you're building the Stone-Cech compactification via ultrafilters here? Since filters are closed upwards, the principle filter at contains , and thus is contained in the clopen set .
- Given a sequence , saying that this sequence converges to means that any closed set , there is an such that for all , .--203.97.79.114 (talk) 09:56, 3 August 2010 (UTC)
Thanks this is very helpfull. From what you have said, I see now, that for every infinite sequence of ultrafilters there exists an open set that contains an infinite number of ultrafilters from that sequence, since for every A in the original topological space X, either A is in infinite number of ultrafilters or the complement of A is in infinite number of ultrafilters. But, How can I show that every sequence of ultrafilters has a convergence subsequence in this Stone-Cech topology. In other words, I guess, how can I show or be convinced that the Stone-Cach compactification is indeed compact? Thanx! —Preceding unsigned comment added by Topologia clalit (talk • contribs) 10:54, 3 August 2010 (UTC)
number of total order relations
If A is a set with 10 elements how many total order binary relations are possible on A. Thanks -Shahab (talk) 13:56, 3 August 2010 (UTC)
- The number of total orders on an n-element set A is equal to the number of bijections from A to {1, 2, 3, ..., n}, which is equal to the number of permutations of {1, 2, 3, ..., n}, which is n!. Algebraist 14:00, 3 August 2010 (UTC)
- Thanks Algebraist, but can you also tell me the proof of this. Clearly a bijection is not always a total order, so the proof cant be that total order and bijections are identical, and hence we have this result. Thanks-Shahab (talk) 14:14, 3 August 2010 (UTC)
- There's a natural bijection between the set of bijections from A to {1, 2, 3, ..., n} and the set of total orders on A: the bijection f corresponds to the order where a<b iff f(a)<f(b) (where the second < is the natural order on {1, 2, 3, ..., n}. Algebraist 14:17, 3 August 2010 (UTC)
- Thanks Algebraist, but can you also tell me the proof of this. Clearly a bijection is not always a total order, so the proof cant be that total order and bijections are identical, and hence we have this result. Thanks-Shahab (talk) 14:14, 3 August 2010 (UTC)
Ambiguity in Number Theory
Here is the discussion moved from above:
- Do any reputable mathematicians actually believe there is any ambiguity in what we mean when we ask whether a statement in number theory is True or False?
- Of course, Gödel tells us that you can't possible complete the axiomatic system of natural numbers, which is to say, no matter how many axioms you add, there will always be statements that are independent of your set of axioms. However, backing away from the limited scope of axiomatic systems, my question is this: is it conceivable that there could be two models of the natural numbers, both "standard" in a sense that can't quite be stated fully in a purely axiomatic sense, that have different truth values for a given statement? I think the answer is no.
- In contrast, set theory seems to be quite ambiguous in the sense that it is certainly conceivable that we could have two perfectly reasonable models of set theory, in one of which the Continuum hypothesis is true, and in the other of which it is false, and we have no clear reason from a purely set theoretic standpoint to prefer one or the other (of course, I could pick any other independent statement in place of the Continuum hypothesis, if it turns out someone demonstrates in the future that there is a clear ironclad reason that the continuum hypothesis ought to be true or false). I emphasize that I don't mean this in the sense that one is more or less useful than the other, but rather, in the sense that one might represent "true" set theory and the other might clearly not be what we intend to mean when we say "set theory". --COVIZAPIBETEFOKY (talk) 16:10, 2 August 2010 (UTC)
- OK, I have to jump in here. No, in fact that is not possible. Any two "reasonable" models of set theory must agree on the truth value of CH. Conditions for the models to be "reasonable" in this sense: First, both should be wellfounded models (that is, not just neither thinks there is an infinite descending epsilon chain, but there really isn't an infinite descending epsilon chain in either model). Second, both models, after taking their Mostowski collapses (so that they have the true natural numbers), should contain all sets of natural numbers, and all sets of sets of natural numbers.
- If you have two models like that, they agree on the truth value of CH, and the value they agree on is the correct truth value. --Trovatore (talk) 07:46, 5 August 2010 (UTC)
- Are you saying that in a "reasonable" model, CH is necessarily true? Tkuvho (talk) 08:35, 5 August 2010 (UTC)
- No, not at all. I'm saying that all such models agree on the truth value of CH. Which way they agree, we don't know at the current time. --Trovatore (talk) 16:35, 5 August 2010 (UTC)
- This is very intriguing. Is this your own work? How does one prove this sort of result? Tkuvho (talk) 11:27, 6 August 2010 (UTC)
- It's actually trivial. CH is equivalent to a sentence of third-order arithmetic ( in fact: "there exists a linear order on P(ω) whose every proper initial segment is countable"), and Trovatore's condition says exactly that the parts of the two models corresponding to third-order arithmetic are the same. What I don't understand is why on earth should this condition be considered "reasonable".—Emil J. 11:45, 6 August 2010 (UTC)
- The point I'm really getting at is that there's a certain rather ill-conceived point of view that attempts to maintain a version of realism (there is a model of this or that) while maintaining that propositions like CH are not determinate. If there are models, then we should be able to ask questions of them like "does such and such a model have all subsets of its naturals?". And you don't even have to go all the way to P(P(omega)) to see that CH must be determinate; all you need to do is interrogate wellfounded models that contain all of P(omega). If all such models agree on the truth value of CH, then they are correct. On the other hand, if there are two such models that disagree, then CH is true. --Trovatore (talk) 15:27, 6 August 2010 (UTC)
- In an attempt to understand these arguments better, I read through continuum hypothesis but was unable to find anything relevant to the question of simulataneous truth or falsity of CH in various models. Could such information be added? Is there another page that may have relevant information? Tkuvho (talk) 07:10, 8 August 2010 (UTC)
- The point I'm really getting at is that there's a certain rather ill-conceived point of view that attempts to maintain a version of realism (there is a model of this or that) while maintaining that propositions like CH are not determinate. If there are models, then we should be able to ask questions of them like "does such and such a model have all subsets of its naturals?". And you don't even have to go all the way to P(P(omega)) to see that CH must be determinate; all you need to do is interrogate wellfounded models that contain all of P(omega). If all such models agree on the truth value of CH, then they are correct. On the other hand, if there are two such models that disagree, then CH is true. --Trovatore (talk) 15:27, 6 August 2010 (UTC)
- It's actually trivial. CH is equivalent to a sentence of third-order arithmetic ( in fact: "there exists a linear order on P(ω) whose every proper initial segment is countable"), and Trovatore's condition says exactly that the parts of the two models corresponding to third-order arithmetic are the same. What I don't understand is why on earth should this condition be considered "reasonable".—Emil J. 11:45, 6 August 2010 (UTC)
- This is very intriguing. Is this your own work? How does one prove this sort of result? Tkuvho (talk) 11:27, 6 August 2010 (UTC)
- No, not at all. I'm saying that all such models agree on the truth value of CH. Which way they agree, we don't know at the current time. --Trovatore (talk) 16:35, 5 August 2010 (UTC)
- Are you saying that in a "reasonable" model, CH is necessarily true? Tkuvho (talk) 08:35, 5 August 2010 (UTC)
- Do you believe reasonable models of set theory should agree on every proposition that can be expressed in the language of set theory? --COVIZAPIBETEFOKY (talk) 21:58, 5 August 2010 (UTC)
- Even in number theory you can get things like Goodstein's theorem which cannot be proved just with Peano's axioms and first order logic. It is quite possible for new axioms to be set up that are perfectly acceptable and prove more than can be done now. Dmcq (talk) 16:56, 2 August 2010 (UTC)
- Wow, er... that wasn't my question at all. Did I not state it clearly enough? I even linked to Gödel's theorem, which should indicate that I already know there are unprovable propositions in any system of natural numbers that includes both addition and multiplication (and I did know about that particular example, although the example is irrelevant to the general principle). --COVIZAPIBETEFOKY (talk) 18:04, 2 August 2010 (UTC)
- Do any reputable mathematicians actually believe there is any ambiguity in what we mean when we ask whether a statement in number theory is True or False? Yes, for example ultrafinitists. Or this guy: [1]. 67.122.211.208 (talk) 18:08, 2 August 2010 (UTC)
- I'm very ignorant on this topic but I would like to ask the logicians: if somehow someone managed to "prove" ZFC is consistent/inconsistent, how do you know the framework he got his metaproof from is consistent? You could try metameta proofs but then how do you know that's correct? This obviously goes on forever. And also, if we adopt formalism, we don't believe in any models what not but there's truth about the sentences etc in the realist sense, for example if you metaproof an infinite collection of formulas are theorems, so can we call that formalistic realism? Money is tight (talk) 04:55, 3 August 2010 (UTC)
- I don't know much about proofs of the consistency of an axiomatic system, except for: while such a proof cannot be obtained from within the system unless the system turns out to be inconsistent after all, it doesn't necessarily have to occur from a strictly stronger system either. Of course, that doesn't mean the system that proves the consistency can be known for certain to be consistent; there will never be complete certainty.
- As for "proofs" of inconsistency of a system, there is only one kind as far as I am aware, and they are quite indisputable: prove a statement and its negation. --COVIZAPIBETEFOKY (talk) 14:49, 3 August 2010 (UTC)
- I'm very ignorant on this topic but I would like to ask the logicians: if somehow someone managed to "prove" ZFC is consistent/inconsistent, how do you know the framework he got his metaproof from is consistent? You could try metameta proofs but then how do you know that's correct? This obviously goes on forever. And also, if we adopt formalism, we don't believe in any models what not but there's truth about the sentences etc in the realist sense, for example if you metaproof an infinite collection of formulas are theorems, so can we call that formalistic realism? Money is tight (talk) 04:55, 3 August 2010 (UTC)
- ZFC proves that there is a minimal model of first order arithmetic. All other models are tail extensions of this one. So in this sense (fixing your universe of set theory), there's a "proper" model of elementary number theory, and you could take Truth to be as interpreted in this model. —Preceding unsigned comment added by 203.97.79.114 (talk) 08:57, 3 August 2010 (UTC)
Thanks for the responses, guys. I have some follow-up questions, but unfortunately I also have other priorities, so it'll take me a while to compile them together. Feel free to add any further contributions in the meantime. --COVIZAPIBETEFOKY (talk) 14:37, 3 August 2010 (UTC)
- Thanks for your respone COVIZAPIBETEFOKY. As I said I'm not at all familiar with this subject (did a tiny bit a while ago but I'm too busy doing math I need for research) so let me tell you a simple and weird philosophical problem of mine. Say we have a theory with one binary relation R, and we have the axioms (1) for all x xRx and (2) (for all x xRx) implies (for all x not related to x), so we see a contradiction by using modus pendus. But by modus pendus we reasoned, and I know this kind of "reasoning" is just the mechanical deduction and not "intuitive reasoning", but still how do we know that obviously-correct-reasoning is correct? I know you must be like wtf, and I know this is really weird. Perhaps when I have time I'll think about the philosophical side more Money is tight (talk) 15:09, 3 August 2010 (UTC)
- Well, in the context of an axiomatic system, what's "correct" is irrelevant to what's valid within the system. We lay out very explicit rules for what's valid and what's not valid, in the form of rules of inference and axioms. In most systems, Modus ponens is a rule of inference, and therefore valid as a step in a proof. It is, however, perfectly conceivable to produce a system in which MP is not a rule of inference. That doesn't change its validity within most of the systems that we speak of in normal mathematical discourse. --COVIZAPIBETEFOKY (talk) 02:48, 4 August 2010 (UTC)
Correct me if I'm wrong, but I'm pretty sure both of the examples that 67.122.211.208 gave are not quite what I'm asking for; they are people who believe that number theory is either outright inconsistent or that it is nonsense not worth studying. My question refers to people who believe in the inherent concept of number theory, but don't believe that there is only one platonic ideal of what a model of number theory should look like exactly. Of course, this is well outside the bounds of mathematical discourse and quite blatantly into philosophy, so possibly it is a question not worth discussing too much. I'm not entirely sure how to justify my own belief that number theory ought to only have one reasonable model, except to say that it's obvious, because in number theory, we can name every object, at least in theory (starting with 0, then S0, SS0, SSS0, and so on).
203.97.79.114's point seems silly to me, since having a reasonable model of set theory is clearly quite a stronger statement than having a reasonable model of number theory (in the sense that it must include a reasonable minimal inductive set containing the empty set, serving as our set of natural numbers, and much more). Maybe there's some merit to it that I don't see, though. --COVIZAPIBETEFOKY (talk) 11:43, 6 August 2010 (UTC)
matrix maximizing algorithm
I saw this problem in a computer programming competition and while I found it trivial to write a program to perform the task, I would like to know if this is a named problem in mathematics so I can see if there are better well-known algorithms. The problem:
- Given an mxn matrix of positive integer values from zero to 2^7. Alter the matrix by converting non-zero values to zero such that no
columnrow contains more than one non-zero number and no column contains more than one non-zero number and the total sum of all numbers in the matrix is maximized. There may be more than one maximum solution for a given matrix.
I did it two ways. The first, which I know will not work in special cases, is to remove the lowest number in any row/column with more than one value until there is no row/column with more than one value. That passed the test in the competition. I wrote another version which attempted removing each number, one at a time, in a breadth-first search until it tried all combinations of removals and picked one of the maximized solutions. That works, but is obviously very cost-intensive. Therefore, I am interested in reading about better solutions. -- kainaw™ 14:53, 3 August 2010 (UTC)
- This is the Assignment problem.
- There's a typo in your problem description, you have "column" twice. -- Meni Rosenfeld (talk) 15:14, 3 August 2010 (UTC)
- Thanks. I just checked the index of my discrete math book (where 99% of programming competition problems come from) and this isn't in there. Looks like the Hungarian algorithm is what I was expected to write. -- kainaw™ 16:07, 3 August 2010 (UTC)
- Correction... Searched my PDF copy and it is briefly mentioned in the marriage problem section - which is also a good reference for this particular problem except that the marriage problem uses a nxn matrix, not an mxn matrix. -- kainaw™ 16:51, 3 August 2010 (UTC)
Tensor product
Ok the definition of "linear in each variable" is a little dodgy when we talk about infinite tensor products. How about this:
Given a collection Mi of R modules, call a map L defined on their direct product linear in i (index/variable) if for every two tuple x,y such that x(j)=x(j) for every j not equal to i, then L(z)=L(x)+L(y), where z(j)=x(j) for j different from i and z(i)=x(i)+y(i). And for every tuple x and scalar a in R, L(z)=aL(x), where z(i)=ax(i) and same as x everywhere else. L is called multilinear if it's linear in every index.
The relations to make the tensor product in the free module generated by the direct product can be done in similar ways. Am I correct? I find "linear in each variable" in the usual sense quite hard to interpret when the direct product is infinite Money is tight (talk) 14:56, 3 August 2010 (UTC)
Polychora
In terms of side length, what's the hypervolume of each of the regular polychora? --138.110.25.31 (talk) 19:51, 3 August 2010 (UTC)
- I assume that you refer to the four-dimensional regular polyhedra, or convex regular 4-polytopes; and I assume that the side length is 1. The tesseract has volume 1 (proof omitted:-); actually, by definition). For the others, you just extrapolate the ordinary methods from (euclidean) geometry in calculating the volumes; with the important observation that the four-dimensional volume of a four-dimensional pyramid is (base volume) × height / 4 .
- The easiest (non-trivial) one to calculate is the volume of the pentachoron. As you hopefully know, the tetrahedron has volume , and the distance between its barycentre (let us call it B) and any vertex (V, say) is . Now, imagine the tetrahedron as a "basis body" in a pentachoron, with its fifth vertex, say W, outside it. We have a right angle at VBW, and VW has length 1; whence and by the pythagorean theorem, the height of the pentachoron is
- ; whence its volume is
- if I calculated correctly (check it by yourself!).
- The remaining four volumes are somewhat more complicated to calculate by this method, since the polytopes must be divided into several four-dimensional pyramids each. I think that the easiest way to do this is to let all pyramids be congruent, with the boundary polyhedra for bases, and a common "top" at the barycentre of the respective polytope. JoergenB (talk) 17:41, 8 August 2010 (UTC)
A more general question
Should we add the volumes to the data in tables and boxes for these six "Platonic bodies", and for the three corresponding larger dimensional families? JoergenB (talk) 17:41, 8 August 2010 (UTC)
LaTeX, more than one line of stuff underneath something
Okay, what I mean is I want to be able to type a sum with two lines of description, such as for an Eisenstein series
- .
I used \stackrel there but note that the top line is smaller. I see in books often where they do it and the two lines are same size font. Thanks. StatisticsMan (talk) 21:28, 3 August 2010 (UTC)
- There is a command "\substack" which does exactly what you want in AMS-LaTeX, but it isn't available on Wikipedia, it seems. --Tango (talk) 03:08, 4 August 2010 (UTC)
- \substack is indeed the proper way to do it. On Wikipedia, one can emulate it with matrices:
- —Emil J. 12:09, 4 August 2010 (UTC)
- Sweet, thanks a lot both of you. StatisticsMan (talk) 13:10, 4 August 2010 (UTC)
- \substack is indeed the proper way to do it. On Wikipedia, one can emulate it with matrices:
August 4
Hi, Can ZANyone Explain why is the Stone-Cech Compactification, defined by the space of ultrafilters, is a compact space? —Preceding unsigned comment added by Topologia clalit (talk • contribs) 07:31, 4 August 2010 (UTC)
- How are you making the Stone–Čech compactification out of ultrafilters? The only way I know only works for discrete spaces. Algebraist 09:23, 4 August 2010 (UTC)
- The entry claims you can make it using maximal filters on the partial order of zero-sets. It's not hard to show that the original space embeds densely in this new space, that the new space is compact, and that it has the universal property. It's not clear to me, however, why it's hausdorff.203.97.79.114 (talk) 10:52, 4 August 2010 (UTC)
- Suppose F and G are distinct maximal filters. Then there exists a zero-set A in F that is not in G. Since G is maximal, it must contain a zero-set B disjoint from A. Let f and g be functions with zero-sets A and B respectively. Then |f|−|g| is strictly negative on A and strictly positive on B. Setting U=(|f|−|g|)−1(−∞,0) and V=(|f|−|g|)−1(0,∞), we have that U and V are disjoint cozero sets containing A and B respectively, which correspond to disjoint basic open sets in the compactification containing F and G. Algebraist 11:56, 4 August 2010 (UTC)
- The entry claims you can make it using maximal filters on the partial order of zero-sets. It's not hard to show that the original space embeds densely in this new space, that the new space is compact, and that it has the universal property. It's not clear to me, however, why it's hausdorff.203.97.79.114 (talk) 10:52, 4 August 2010 (UTC)
Descrete spaces will be helpfull for me too.. Suppose we take the descerete case. I don't understand, Why is the space of ultrafilters defined on X is compact? In the topology we have mentioned a few days ago.. I think that in here it is specified that the space of ultrafilters defined over X is compact Hausdorff for any topological space X: http://en.wikipedia.org/wiki/Stone%E2%80%93%C4%8Cech_compactification Topologia clalit (talk) 09:57, 4 August 2010 (UTC)
- The ultrafilter topology is generated by the basis of closed sets CA={ultrafilters F such that A∈F}m where A ranges over subsets of X. Note that CA∩CB=CA∩B, and similarly for any finite intersection. Suppose that we have an infinite family {Ai|i∈I} of subsets of X, such that any finite subset of the CAi has nonempty intersection. But then any finite subset of the Ai must likewise have nonempty intersection, so we can find a filter (and hence an ultrafilter) containing all of the Ai. This ultrafilter is in the intersection of the CAi, which is thus nonempty, and so the space of ultrafilters is compact. Algebraist 10:10, 4 August 2010 (UTC)
Thanks!!! Topologia clalit (talk) 10:09, 7 August 2010 (UTC)
{Ø}
What is {Ø}?199.126.224.156 (talk) 09:58, 4 August 2010 (UTC)
- The set whose only element is the empty set. Algebraist 10:01, 4 August 2010 (UTC)
- An alternative notation for which is {{}}. -- The Anome (talk) 13:52, 5 August 2010 (UTC)
- Under a standard notation, it is also the number one, represented as 1.--Shahab (talk) 13:08, 4 August 2010 (UTC)
Geometry problem
Since the last programming competition question was answered so quickly, I think I'll try another one that has been bothering me for a long time. I asked before on the computing desk, but the answers didn't really answer the question. This is a paraphrased question from a programming competition I was in many years ago. Note, all numbers are decimal, not integer numbers.
- Given three (x,y) coordinates, you have the definition of a triangle. Given three more positive non-zero numbers, you have defined three circles, each number being a radius. Is it possible for all three circles to fit in the triangle without overlapping the edges of the triangle or each other. Edges may touch, but not overlap.
My program was deemed correct, but I know it was wrong because I only tested the situation that the smallest circle goes into the smallest angle corner of the triangle and the largest circle goes into the largest angle corner - leaving the medium circle for the medium angle corner. There is another situation where the circles may be lined up along one side of the triangle, but not fit into the three corners. Is there a simple solution to this problem or is it required to be a complicated task of testing every possible layout for organizing the circles inside the triangle? -- kainaw™ 12:19, 4 August 2010 (UTC)
- There's something missing here. If the triangle is quite big and the 3 radii are quite small then they fit easily. If your phrase "Given three more positive non-zero numbers" is parsed "Given (three more) (positive non-zero numbers)" then that interpretation is possible. If it is parsed "Given three (more positive) non-zero numbers" then more positive than what - the other numbers are x,y pairs. What am I not seeing? -- SGBailey (talk) 20:56, 4 August 2010 (UTC)
- Can't say I understand either. There's also no restriction about what planes the circles can be on, so the radii might stretch to the z-axis and allow a huge amount of circles. And what if you have cases where your circle has a huge radius? You can't ever fit that without overlapping something? Yea, I must be missing something too. --Wirbelwindヴィルヴェルヴィント (talk) 23:16, 4 August 2010 (UTC)
- The question is to determine the values of the parameters for which it is possible to fit the circles inside the triangle. For example, if there were only one circle, the answer would be given by the radius r of the inscribed circle: if the radius of the circle is less than r, it can fit inside, otherwise not. For a pair of circles, one gets smaller triangles inside the big triangle for allowable locus for the center of each circle, and the solution is determined by calculating the maximal distance between a vertex of the first small triangle and a vertex of the second small triangle. Tkuvho (talk) 23:41, 4 August 2010 (UTC)
- Can't say I understand either. There's also no restriction about what planes the circles can be on, so the radii might stretch to the z-axis and allow a huge amount of circles. And what if you have cases where your circle has a huge radius? You can't ever fit that without overlapping something? Yea, I must be missing something too. --Wirbelwindヴィルヴェルヴィント (talk) 23:16, 4 August 2010 (UTC)
- The question uses "given" to mean "you are given". So, you are given something like: (1,4.5) (-3.2,9.3) (0,45) 23 41.6 21. The first three x,y coordinates define a triangle. The second three numbers define three circles. Will those three circles fit in the triangle? It isn't a question about one specific case. It is a question about coming up with an algorithm that will work for EVERY possible set of x,y coordinates and radius values. -- kainaw™ 00:01, 5 August 2010 (UTC)
- You wrote: "There is another situation where the circles may be lined up along one side of the triangle, but not fit into the three corners." Can you provide an example? -- 119.31.126.81 (talk) 12:37, 5 August 2010 (UTC)
- Triangle sides 1, 100, 100; Circle radii 0.9, 0.9, 0.9. -- Meni Rosenfeld (talk) 15:38, 5 August 2010 (UTC)
- Exactly. So, the only arrangements that I can think of are placing the circles into the three corners and checking for overlap or placing the circles in a line and checking for overlap. I don't know of any other arrangement for the circles that would work when those two fail. I also can't think of a shortcut to make this an easier problem. (Also, the original problem was even more complicated. They weren't just circles. There was two parallel planes. The triangle extended over both planes to make a triangular container. The circles had a separate radius on each plane, making them look like little hats with one wide radius and one smaller radius. You were allowed to flip the circles over to try and make them fit better. So, I figure the real problem was performing the "does it fit" algorithm and flipping the circles if they don't fit. That is why I assume that the "does it fit" algorithm should be easy.) -- kainaw™ 15:53, 5 August 2010 (UTC)
- Triangle sides 1, 100, 100; Circle radii 0.9, 0.9, 0.9. -- Meni Rosenfeld (talk) 15:38, 5 August 2010 (UTC)
Sloppy Notation?
I'm presently reading through a set of notes on Vector Calculus and have met a result that I understand but I'm not sure that the notational rules have been observed.
In the term with both an epsilon and a delta, I was under the impression that you're not allowed to let j=k and then sum over j in the delta and simultaneously leave the epsilon, by which the delta is multiplied, unchanged. Is this correct notation? Thanks asyndeton talk 13:40, 4 August 2010 (UTC)
- Looks like a typo. Final expression Should be
- My mistake, I just copied and pasted without amending it for my purposes. But my original question still stands, unless you're implying that having was the only mistake in the whole thing? asyndeton talk 15:22, 4 August 2010 (UTC)
- I can't make any sense of your question. Where has anyone let j=k and then summed over j in the delta and simultaneously left the epsilon, by which the delta is multiplied, unchanged? Algebraist 15:46, 4 August 2010 (UTC)
- My mistake, I just copied and pasted without amending it for my purposes. But my original question still stands, unless you're implying that having was the only mistake in the whole thing? asyndeton talk 15:22, 4 August 2010 (UTC)
- (edit conflict) Yes, with instead of , the expression is correct. The step that is omitted is:
- Of course, is 0 for all i, since is 0 if j = k and is 0 if j ≠ k. But this is just saying that is the zero vector everywhere
, which is intuitively clear because, considered as a vector field, is purely radial and so has no rotation. Gandalf61 (talk) 15:56, 4 August 2010 (UTC)
- (edit conflict) Yes, with instead of , the expression is correct. The step that is omitted is:
Homeomorphisms of R3


I was thinking about quotient spaces of the sphere. Take the sphere an identify the North and South poles. This can be done many ways; but I have two examples in mind. We can take the poles and pull them away from the centre, pull them around outside of the sphere and then glue them together. This will give a pinched torus (see the left hand image). The other way would be to push the poles into the sphere towards the centre, and then glue them when they meet (see the right hand image). I can see that these are embeddings of the quotient space S2/S0 into R3. I was wondering:
- Is there a homeomorphism of R3 that takes one to the other?
- Given two embeddings of ƒ, g : X → Y, can we find a homeomorphism h : Y → Y that carried ƒ(X) to g(X)?
— Fly by Night (talk) 16:08, 4 August 2010 (UTC)
- The figure on the left has the property that the (open) interior of the pinched torus is homeomorphic to a 3-ball. The figure on the right has the property that the interior of the torus is homeomorphic to a circle times a disk. Therefore there is no such homeomorphism. Tkuvho (talk) 17:15, 4 August 2010 (UTC)
- The image on the right isn't a torus. There's no hole in the middle. Denote it by A then the fundamental group is π1(A) ≅ Z. The loops around the outside of the outside of A can be deformed into a point. (The inner circle of a torus has been identified, i.e. is just a single point. The singularity of the image.) I think that the interior of the object on the right is homeomorphic to the interior of a solid torus. So you would be right: there is no homeomorphism. Thanks a lot for your comments. — Fly by Night (talk) 18:01, 4 August 2010 (UTC)
- The figure on the left has the property that the (open) interior of the pinched torus is homeomorphic to a 3-ball. The figure on the right has the property that the interior of the torus is homeomorphic to a circle times a disk. Therefore there is no such homeomorphism. Tkuvho (talk) 17:15, 4 August 2010 (UTC)
This raises another question. Denote the pinched torus by P and the object on the right by A. It seems that the interior of P is homeomorphic to the exterior of A and the interior of A is homeomorphic to the exterior of P. Is there a name for this property? Have these kind of objects been studied before? — Fly by Night (talk) 18:09, 4 August 2010 (UTC)
- If you complete R3 to S3 by adding a point at infinity, then the two figures are identical, modulo switching interior and exterior. You might be interested in related material at surgery theory. Tkuvho (talk) 19:26, 4 August 2010 (UTC)
- But by adding a point at infinity we change the topology of the host space. Besides, it's special to R3. Have you any more general thoughts? Say that a space X is embedded in a space Y, then how many possible, non-homeomorphic images are there? Given two embeddings ƒ, g : X → Y of a compact 2-dimensional space X into a 3-dimensional space Y then what does in mean for the interior of ƒ(X) to be homeomorphic to the exterior of g(X) while the interior of g(X) is homeomorphic to the exterior of ƒ(X)? — Fly by Night (talk) 19:36, 4 August 2010 (UTC)
- Adding a point at infinity is not special to R^3: see One-point compactification.—msh210℠ 19:43, 4 August 2010 (UTC)
- Okay, fine. Could you now please address the question? — Fly by Night (talk) 21:13, 4 August 2010 (UTC)
- Note that the exterior of the figure on the right is homeomorphic to a punctured ball, i.e. a 2-sphere times an open interval. Tkuvho (talk) 08:38, 5 August 2010 (UTC)
- A 2-sphere times an open interval is an open thick shell. I've never heard of that described as a "punctured ball"; it seems an odd name. You are correct in your description of the exterior, though. It could also be described as R3 minus an open ball. --Tango (talk) 14:25, 5 August 2010 (UTC)
- Note that the exterior of the figure on the right is homeomorphic to a punctured ball, i.e. a 2-sphere times an open interval. Tkuvho (talk) 08:38, 5 August 2010 (UTC)
- Okay, fine. Could you now please address the question? — Fly by Night (talk) 21:13, 4 August 2010 (UTC)
- Adding a point at infinity is not special to R^3: see One-point compactification.—msh210℠ 19:43, 4 August 2010 (UTC)
- But by adding a point at infinity we change the topology of the host space. Besides, it's special to R3. Have you any more general thoughts? Say that a space X is embedded in a space Y, then how many possible, non-homeomorphic images are there? Given two embeddings ƒ, g : X → Y of a compact 2-dimensional space X into a 3-dimensional space Y then what does in mean for the interior of ƒ(X) to be homeomorphic to the exterior of g(X) while the interior of g(X) is homeomorphic to the exterior of ƒ(X)? — Fly by Night (talk) 19:36, 4 August 2010 (UTC)
August 5
Countable Compact Connected Hausdorff Space
I know that there is a rather obvious proof that no nontrivial space has all these properties, just can't remember it and google isn't very helpful. It's been on the edge of my mind for a while, can anyone be of help? 66.202.66.78 (talk) 07:07, 5 August 2010 (UTC)
- One proof uses the Baire category theorem. Algebraist 07:31, 5 August 2010 (UTC)
- There's an easier proof: compact hausdorff are normal, so assume there are two distinct points x,y. By Urysohn's lemma there's a continuous function from X to [0,1] such that f(x)=0 and f(y)=1. Now X is connected so this function must be surjective, so X is at least continuum. Money is tight (talk) 05:43, 6 August 2010 (UTC)
how "unpredictable enough" system is useful?
From second paragraph of Experimental system, "A successful experimental system must be stable and reproducible enough for scientists to make sense of the system's behavior, but variable and unpredictable enough that it can produce useful results".
I can understand that system must be variable enough to produce useful results, but I cannot understand why system must be unpredictable enough?
Can someone give a simple explanation and example? - manya (talk) 07:38, 5 August 2010 (UTC)
- If you can predict the outcome of an experiment, there is no point in performing the experiment. I know that I get wet when going out in the rain, so doing so is not much of an experiment. Bo Jacoby (talk) 08:37, 5 August 2010 (UTC).
- I thought so. But I think 'variables' are input parameters, and for tested/experimented set of parameters the output is predictable because system is reproducible. For untested set of data, how do we know whether it is predictable until experiment is done? Is this 'experimental system' universal (chemistry, physics etc) or specific to bio field? How a system (that is "physical, technical and procedural basis") be predictable or unpredictable. I have been under strong impression that theory proposes (predicts) and experiment verifies (proves). - manya (talk) 10:37, 5 August 2010 (UTC)
- When there are conflicting theories, an experiment settles the conflict. See for example the Bell test experiments. Bo Jacoby (talk) 11:25, 5 August 2010 (UTC).
creating diagonal matrix with only basic operations?
I would like to "convert" a vector to a diagonal matrix with the elements of the vector on the main diagonal. This can be solved with an easy loop, but the problem is, that I need to do it by using only basic mathematical operations: multiplication and addition (to transpose is allowed), as I need those matrices as variables in a function which I intend to derive, integrate, etc. I originally needed to do an element-wise multiplication (like A .* B instead of A * B in Matlab), so I tried the following:
[A;B;C] * Q * [X;Y;Z] = [AX;BY;CZ]
What I would like to have is a Q which transforms [A;B;C] to [A 0 0; 0 B 0; 0 0 C] The problem was, if I wrote it as Q = [1 1 1] * W (just to have a 3*3 matrix) the
[A A A; B B B; C C C] * [a b c; d e f; g h i] = [A 0 0; 0 B 0; 0 0 C]
system does not have a solution: we get contradictions like a+d+g=1 and a+d+g=0
Does this mean that this is unsolvable? Or is my approach wrong? Actually, as the vectors can be quite big, I would prefer a solution to the elementwise multiplication without using square matrices, if possible at all, I just couldn't find one. --131.188.3.20 (talk) 10:40, 5 August 2010 (UTC)
- There is no matrix Q such that is the diagonal matrix with x on the diagonal. This is easy to see; the rank of x, and hence xQ, is at most 1, while the rank of a general 3x3 diagonal matrix is 3.
- I can't understand why you need this, so maybe you should explain your application a bit more. -- Meni Rosenfeld (talk) 11:38, 5 August 2010 (UTC)
- I just need what I described in the introduction: to do an element-wise multiplication (like .* in Matlab) with basic arithmetical operations. It is enough if I find a solution for vectors. So the goal: given two vectors A and B, construct a vector C where each element Ci is Ai*Bi . What is important, to do it in such a way, that I can use it fo perform algebraic operations and even some calculus at the end. Otherwise it would be easy to write a program that loops through the vector. --131.188.3.21 (talk) 14:48, 5 August 2010 (UTC)
- Element-wise multiplication is the basic arithmetical operation, also known as Hadamard product. There's no way to reduce it to "more basic" arithmetic operations. You just write and continue to do whatever you want. For example, if A and B are functions of t, you have . -- Meni Rosenfeld (talk) 15:32, 5 August 2010 (UTC)
- Wow, thanks for the idea. So I can do anything with it, I mean to play around with it in equations like it was just a "normal" multiplication? The no way to reduce it means that it is impossible to build if out of other operations, and I can give up searching for it? Our article does not tell much about it. --131.188.3.21 (talk) 15:45, 5 August 2010 (UTC)
- You can build it from other operations, but as an informal observation, they won't be more basic and I doubt they'll help you in manipulating it. For example, you can define a linear transformation , is the diagonal matrix with x on the diagonal. Then you'll have , but doing calculus with this will be tricky at best. You certainly can think about other creative ways to construct it.
- This operation is in many ways similar to ordinary multiplication of numbers. Common sense is usually enough to tell what will or won't work with it, and where that fails proving basic properties should be fairly simple. -- Meni Rosenfeld (talk) 15:57, 5 August 2010 (UTC)
- The derivation gives me headaches: if I have , where A and B are constants and X varies in t, and the AX has the same dimensions as B, but A or X alone don't, than deriving it will lead me to which is not possible. Unless I got something wrong. --131.188.3.20 (talk) 00:28, 6 August 2010 (UTC)
- In case this was the problem, note that element-wise multiplication is not "associative with" matrix multiplication. In general . By itself it's commutative and associative, though. So you can write the above as , but not as . -- Meni Rosenfeld (talk) 06:25, 6 August 2010 (UTC)
- Yes, I knew (I mean, I suspected and proved for myself with counterexamples) they are not associative, but the problem lies elsewhere. I think I made a mistake with the notation. Let x be a vector and I want to derive by x. will lead to , but what if the dimensions of A and B are different? Like, for example, x is a n*1 vector, and B an m*1, and A an m*n matrix. —Preceding unsigned comment added by 131.188.3.20 (talk) 08:40, 6 August 2010 (UTC)
- I think these cases work if you extend the meaning of so that, for example, and so on. Note that matrix multiplication and element-wise multiplication correspond to two very different ways of interpreting matrices (either as linear transformations or as just a bunch of numbers), and so the results might not always be elegant when you try to use them together.
- If you haven't already, you may want to look at Matrix calculus which discusses differentiating with respect to a vector (though not in relation to the Hadamard product). -- Meni Rosenfeld (talk) 09:32, 6 August 2010 (UTC)
- This interpretation is useful, but I don't see what to do with a
- To turn in into or does not make any sense, as the original purpose of A was to make a surjective mapping of "smaller" vector x onto the bigger vector B, so if I just pair first with first and so on, the pairings will not make any sense. (I'm sorry I'm not that good in using the English terminology, but I hope I was understandable) --131.188.3.21 (talk) 10:00, 6 August 2010 (UTC)
- Yes, I knew (I mean, I suspected and proved for myself with counterexamples) they are not associative, but the problem lies elsewhere. I think I made a mistake with the notation. Let x be a vector and I want to derive by x. will lead to , but what if the dimensions of A and B are different? Like, for example, x is a n*1 vector, and B an m*1, and A an m*n matrix. —Preceding unsigned comment added by 131.188.3.20 (talk) 08:40, 6 August 2010 (UTC)
- The derivation gives me headaches: if I have , where A and B are constants and X varies in t, and the AX has the same dimensions as B, but A or X alone don't, than deriving it will lead me to which is not possible. Unless I got something wrong. --131.188.3.20 (talk) 00:28, 6 August 2010 (UTC)
- Wow, thanks for the idea. So I can do anything with it, I mean to play around with it in equations like it was just a "normal" multiplication? The no way to reduce it means that it is impossible to build if out of other operations, and I can give up searching for it? Our article does not tell much about it. --131.188.3.21 (talk) 15:45, 5 August 2010 (UTC)
- Element-wise multiplication is the basic arithmetical operation, also known as Hadamard product. There's no way to reduce it to "more basic" arithmetic operations. You just write and continue to do whatever you want. For example, if A and B are functions of t, you have . -- Meni Rosenfeld (talk) 15:32, 5 August 2010 (UTC)
- I just need what I described in the introduction: to do an element-wise multiplication (like .* in Matlab) with basic arithmetical operations. It is enough if I find a solution for vectors. So the goal: given two vectors A and B, construct a vector C where each element Ci is Ai*Bi . What is important, to do it in such a way, that I can use it fo perform algebraic operations and even some calculus at the end. Otherwise it would be easy to write a program that loops through the vector. --131.188.3.21 (talk) 14:48, 5 August 2010 (UTC)
- Oops, I mean, in this case it should have been not Still, the problem above can come up: A is just a matrix to reorder the elements of x, so it does not make much sense to multiply it to elements of B. --131.188.3.20 (talk) 10:22, 6 August 2010 (UTC)
- Why not? In your case B specifies by what values to multiply each entry of . So it makes sense that instead of multiplying by B after reordering, you preemptively multiply it by A in preparation for the imminent multiplication with x.
- It's possible that the notation should be extended in additional ways in order to deal with more general cases. -- Meni Rosenfeld (talk) 11:37, 6 August 2010 (UTC)
- Thank you, you was very helpful, now I know how to do derivations with the element-wise product :) . However, there are still things that baffle me: it seems very hard to reorder and separate variables, like getting x in . Is there any good source you suggest me to read about the properties of the pointwise product? What I found gave very little useful information about its properties. What I found out by testing is that it's not only not associative but not even distributive with other common operations. --131.188.3.21 (talk) 12:51, 6 August 2010 (UTC)
- Not that I know of. The PlanetMath entry has some basic info and references. -- Meni Rosenfeld (talk) 13:21, 6 August 2010 (UTC)
- Thank you, you was very helpful, now I know how to do derivations with the element-wise product :) . However, there are still things that baffle me: it seems very hard to reorder and separate variables, like getting x in . Is there any good source you suggest me to read about the properties of the pointwise product? What I found gave very little useful information about its properties. What I found out by testing is that it's not only not associative but not even distributive with other common operations. --131.188.3.21 (talk) 12:51, 6 August 2010 (UTC)
- Oops, I mean, in this case it should have been not Still, the problem above can come up: A is just a matrix to reorder the elements of x, so it does not make much sense to multiply it to elements of B. --131.188.3.20 (talk) 10:22, 6 August 2010 (UTC)
Conjectures
What will happen if P=NP, or the Riemann hypothesis is false, or some other conjecture that's obviously true is disproved? --138.110.206.101 (talk) 12:47, 5 August 2010 (UTC)
- Some people will be surprised. (In the mean time, you'd be hard pressed to find a mathematician who thinks these are "obviously true".) Staecker (talk) 13:56, 5 August 2010 (UTC)
- Just about everyone agrees that P!=NP and the Riemann hypothesis is true; many "theorems" are proved based on assuming them. If P=NP or the Riemann hypothesis is false, these would all be invalidated. --138.110.206.150 (talk) 19:45, 5 August 2010 (UTC)
- What will happen? (1) Clay will be 1,000,000 dollars poorer, and (2) the reference desk will be flooded with requests for explanation. Tkuvho (talk) 20:12, 5 August 2010 (UTC)
- Are there that many theorems assuming P ≠ NP? Oliphaunt (talk) 21:12, 5 August 2010 (UTC)
- Most mathematicians think those are the most likely possibilities, but they are far from certain about it. --Tango (talk) 22:09, 5 August 2010 (UTC)
- Did you take a look at our articles on this? From P versus NP problem: "Is P equal to NP? In a 2002 poll of 100 researchers, 61 believed the answer to be no...". 61% is hardly "just about everyone", and "believed" is not the same as "were certain", let alone "think it obvious". From Riemann hypothesis: "The consensus... is that the evidence for it is strong but not overwhelming... there is some reasonable doubt about it."
- The converse exists as well - there are many theorems that assume that P=NP, if it turns out P!=NP then those will be moot. So what? Everyone knows that these theorems are conditional on whether P=NP. It's not like things that were thought to be true will turn out false, it's that things that were thought to be maybe true will turn out false and others to be actually true. -- Meni Rosenfeld (talk) 06:40, 6 August 2010 (UTC)
- Just about everyone agrees that P!=NP and the Riemann hypothesis is true; many "theorems" are proved based on assuming them. If P=NP or the Riemann hypothesis is false, these would all be invalidated. --138.110.206.150 (talk) 19:45, 5 August 2010 (UTC)
Axiom of choice again
This is related to the axiom of choice question I asked a few days back. Suppose we have a relation R on a set A. Suppose further that R is both reflexive and symmetric. I want to find out a cover of the set A, i.e. a collection of nonempty sets Ai such that their union is A, from this relation. The obvious thing seems to pick an x, and define Ax as the set of all y such that (x,y) is in R. Now if this exhausts the set we are done, if not then we pick up another element and continue. My question is what guarantees this procedure is valid. Does the axiom of choice ever enter into the picture and if so, what is the choice function?-Shahab (talk) 13:48, 5 August 2010 (UTC)
- What do you want the procedure to produce? Some condition seems to be missing in the description, because you can trivially construct a cover of A by taking A0 = A.—Emil J. 13:58, 5 August 2010 (UTC)
- Describing this as an iterative procedure (pick an x, then form etc.) is a good heuristic tool, but it may be misleading. For example, if the set of equivalence classes is uncountable, obviously you cannot choose your x's one-by-one. What is happening here is that you are forming all the equivalence classes simultaneously. The axioms of ZF are sufficient for this, as already pointed out by algebraist in the previous discussion. On the other hand, if you want to index by elements of A, you need choice, as already discussed. Tkuvho (talk) 14:15, 5 August 2010 (UTC)
- The cover needs to be related to the relation-Shahab (talk) 14:13, 5 August 2010 (UTC)
- Related in what way?—Emil J. 14:25, 5 August 2010 (UTC)
- I am sorry if my explanation wasnt clear enough.What I want is that each class (I'll call it compatible class, as apparently a symmetric and reflexive relation goes under the name compatible relation) is such that there is an element x in it so that all y, for which we have xRy, are in the same class, and x isnt in any other class. Will simultaneously defining all the classes as [x] = {y: xRy} guarantee this? or I will have to proceed step by step, in which case do I need choice, and how?-Shahab (talk) 14:28, 5 August 2010 (UTC)
- No, that won't work. Try the set {A,B,C} with the relation {(A,B),(A,C)}. Your method would give the cover {A,B,C}, {A,B}, {A,C}. Since every element is in at least two sets in the cover, there is no way you can have an x for each set that isn't in any other set. --Tango (talk) 14:43, 5 August 2010 (UTC)
- Note that the relation is given to be reflexive and symmetric, which isnt the case in your example. Regards-Shahab (talk) 14:48, 5 August 2010 (UTC)
- I know, I just realised that. It's just my bad notation. I meant the smallest relation containing that relation and satisfying the conditions given, but my notation obviously doesn't actually say that. --Tango (talk) 15:05, 5 August 2010 (UTC)
- Okay. I see what you mean.-Shahab (talk) 15:20, 5 August 2010 (UTC)
- I know, I just realised that. It's just my bad notation. I meant the smallest relation containing that relation and satisfying the conditions given, but my notation obviously doesn't actually say that. --Tango (talk) 15:05, 5 August 2010 (UTC)
- Note that the relation is given to be reflexive and symmetric, which isnt the case in your example. Regards-Shahab (talk) 14:48, 5 August 2010 (UTC)
- No, that won't work. Try the set {A,B,C} with the relation {(A,B),(A,C)}. Your method would give the cover {A,B,C}, {A,B}, {A,C}. Since every element is in at least two sets in the cover, there is no way you can have an x for each set that isn't in any other set. --Tango (talk) 14:43, 5 August 2010 (UTC)
- I am sorry if my explanation wasnt clear enough.What I want is that each class (I'll call it compatible class, as apparently a symmetric and reflexive relation goes under the name compatible relation) is such that there is an element x in it so that all y, for which we have xRy, are in the same class, and x isnt in any other class. Will simultaneously defining all the classes as [x] = {y: xRy} guarantee this? or I will have to proceed step by step, in which case do I need choice, and how?-Shahab (talk) 14:28, 5 August 2010 (UTC)
- Related in what way?—Emil J. 14:25, 5 August 2010 (UTC)
Equivalence relation and partitions
Okay here is another problem. Let R be an equivalence relation on A and {A1,...Ak} be a set of subsets on A such that Ai is not a subset of Aj for i≠j and such that a and b are contained in one of the subsets if and only if the ordered pair (a,b) is in R. I need to show that {A1,...Ak} is a partition of A.
I can see that it covers A but why are all Ai's disjoint. Thanks-Shahab (talk) 15:35, 5 August 2010 (UTC)
- I don't think they are necessarily disjoint. Let A={0,1,2,3,4,5} and aRb iff a=b (mod 2). Then let the Ai's be {0,2}, {0,4}, {2,4}, {1,3}, {1,5}, {3, 5}. That seems to satisfy your requirements, but the subsets aren't disjoint. --Tango (talk) 16:43, 5 August 2010 (UTC)
- Thanks. It is an error in the book I am reading then, which contains this question. A kind of relief indeed!-Shahab (talk) 17:02, 5 August 2010 (UTC)
- The book definitely says "Prove" and not "Prove or provide a counter-example"? You should check that my counter-example does work, I may have made a mistake or misunderstood the question (especially since I've heard it 2nd hand). --Tango (talk) 17:13, 5 August 2010 (UTC)
- Yes, I checked it. Your example is right. The problem is from this book (Page 173).-Shahab (talk) 17:32, 5 August 2010 (UTC)
- Did you quote the problem exactly? The link you provided does not offer any preview of the book. -- 119.31.121.87 (talk) 00:14, 6 August 2010 (UTC)
- Strange, it does so in my browser--Shahab (talk) 03:15, 6 August 2010 (UTC)
- Perhaps it is an issue with being in Thailand, although it simple says "No preview available" and does not mention geographic restrictions. -- 112.142.27.47 (talk) 13:14, 6 August 2010 (UTC)
- I get the same message in the UK. --Tango (talk) 16:22, 6 August 2010 (UTC)
- Perhaps it is an issue with being in Thailand, although it simple says "No preview available" and does not mention geographic restrictions. -- 112.142.27.47 (talk) 13:14, 6 August 2010 (UTC)
- Strange, it does so in my browser--Shahab (talk) 03:15, 6 August 2010 (UTC)
- Did you quote the problem exactly? The link you provided does not offer any preview of the book. -- 119.31.121.87 (talk) 00:14, 6 August 2010 (UTC)
- Yes, I checked it. Your example is right. The problem is from this book (Page 173).-Shahab (talk) 17:32, 5 August 2010 (UTC)
- The book definitely says "Prove" and not "Prove or provide a counter-example"? You should check that my counter-example does work, I may have made a mistake or misunderstood the question (especially since I've heard it 2nd hand). --Tango (talk) 17:13, 5 August 2010 (UTC)
- Thanks. It is an error in the book I am reading then, which contains this question. A kind of relief indeed!-Shahab (talk) 17:02, 5 August 2010 (UTC)
August 6
Empirical maximum likelihood problem
Hello everybody
I am struggling with an optimization problem. I have a stochastic computer model with two parameters which I call (nu,M).
With a fixed value for (nu,M) the model produces two outputs which I call (theta,overl) which seem to have a bivariate Gaussian distribution. The distribution depends on the values of (nu,M). I know the "correct" value for (theta,overl).
I know very little about the model's properties, but I can sample from it; a single sample takes about an hour's computing time.
I want to calculate a maximum likelihood estimate for (nu,M).
I feel sure that this must be a standard problem, but googling "empirical maximum likelihood estimate" comes up unhelpful.
Is my problem a special case of a well-known technique? Robinh (talk) 10:19, 6 August 2010 (UTC)
So I'm confused about the proof behind Bessel's correction, and it's driving me insane!
The proof is as follows:
So what I'm not following is how did they get from here:
to here:
??? - 114.76.235.170 (talk) 15:22, 6 August 2010 (UTC)
- and don't depend on i so and . In other words, summing n copies of the same thing is the same as multiplication by n. Rckrone (talk) 16:01, 6 August 2010 (UTC)
- Sir, you are an absolute legend!!! I can't thank you enough for this explanation :-) - 114.76.235.170 (talk) 22:59, 6 August 2010 (UTC)
Define a Pseudo-topology
Define a pseudo-topology as a pair (X,Σ) consisting of a set X and a collection Σ of subsets of X, called open sets, satisfying the following axioms:
- The union of open sets is an open set.
- The intersection of open sets is an open set.
- X and the empty set ∅ are open sets.
Notice that I no longer require a finite intersection of sets for the result to an open set.
- What novel properties does a pseudo-topology have, as opposed to a standard topology?
- Why was the finiteness condition insisted upon for intersections?
— Fly by Night (talk) 19:18, 6 August 2010 (UTC)
- I can't answer the first question, but the second is easy: The prototype for topological spaces is Euclidean space and an infinite intersection of open sets in Euclidean space is not necessarily open. A lot of types of mathematical objects (topological spaces, vector spaces, manifolds, differential manifolds, groups, rings, fields, etc.) are generalisations of very familiar objects (Euclidean space, integers, real numbers, etc.). We try and work out which properties of that familiar object are actually required to get the results we like and those properties become the definition of the generalisation. --Tango (talk) 19:40, 6 August 2010 (UTC)
- Tango, the topology that Fly by Night constructed does have a name, and does have some useful properties (but it is certainly not as useful as the standard notion of a topology): It is called an Alexandrov topology. There are some pretty weird constructions in mathematics, I should add, so it should not be too surprising that people have attempted to study these sorts of topologies before. (One of the most "naturally occuring" though weird topologies is the Zariski topology in algebraic geometry, but even this topology is not in general Alexandrov.) Nonetheless, Alexandrov topologies do actually occur naturally sometimes in set-theoretic and point-set topology. PST 00:36, 7 August 2010 (UTC)
- Just to exhaust other possibilities of "playing with the axioms", I shall note that the requirements that the entire set X and the empty set be open are partially there to ensure that constant functions are continuous. (But the theory would not change much if you removed this requirement and defined a function to be continuous if and only if the preimage of any open set under the function is either open, all of X, or the empty set.) PST 00:43, 7 August 2010 (UTC)
- Tango, the topology that Fly by Night constructed does have a name, and does have some useful properties (but it is certainly not as useful as the standard notion of a topology): It is called an Alexandrov topology. There are some pretty weird constructions in mathematics, I should add, so it should not be too surprising that people have attempted to study these sorts of topologies before. (One of the most "naturally occuring" though weird topologies is the Zariski topology in algebraic geometry, but even this topology is not in general Alexandrov.) Nonetheless, Alexandrov topologies do actually occur naturally sometimes in set-theoretic and point-set topology. PST 00:36, 7 August 2010 (UTC)
- Thanks for your reply, Tango. It's clear that Euclidean space with a metric topology is an intuitive example of a topology. But I was hoping for something more substantial. For example, are the axioms inconsistent if we drop the finiteness of intersections condition? Etc. — Fly by Night (talk) 20:57, 6 August 2010 (UTC)
- You're definitely not going to get any inconsistencies. Just look at the discrete topology on any set - it will satisfy the axioms you listed. It's more likely that these pseudo-topologies turn out to be less interesting/useful/familiar than the standard notion of a topology. You may also be interested by sigma algebra if you've never run into one of those before. J Elliot (talk) 21:01, 6 August 2010 (UTC)
- I shall read that now. Thanks for the link. — Fly by Night (talk) 22:10, 6 August 2010 (UTC)
- It is worthwhile to note two things about the sigma algebra example: Sigma algebras are closed under countable intersections (and hence also under finite intersections) and sigma algebras are closed under countable unions (and hence also under finite unions). (These can be proven by manipulating the axioms and can be a good exercise if you are not familiar with sigma algebras.)
- If you have done measure theory or probability theory, it is easy to appreciate why these axioms are the way they are. The most obvious reason is the same as that given by Tango above: If we allowed uncountable unions of measurable sets to be measurable, accepting that singleton sets in Euclidean spaces are measurable would yield that every subset of Euclidean space is measurable. This would, however, not be very useful since the primary purpose of measurable spaces is to equip them with measures (though there are other purposes, as well) and it is impossible to define a countably additive, translation invariant measure on the set of all subsets of Euclidean space such that the measure of any open cell is its volume in the ordinary sense.
- You can define a subadditive measure on all subsets of Euclidean space that has the other properties; the proof of the Riesz representation theorem for positive linear functionals on a space of continuous complex-valued functions with compact support gives such a construction. Also note that if X is a locally compact Hausdorff space in which every open set is sigma compact, then any positive Borel measure on X that is finite on compact sets must necessarily be regular. Hence the ordinary Lebesgue measure on Euclidean space is a Borel measure. (Again, this can be shown directly using the Riesz representation theorem; in fact, the proof of this general statement (at least the one I know; there could be a simpler proof) relies on the Riesz representation theorem.) Up to multiplication by scalars, in fact, this is the only positive, translation invariant, Borel measure on all Borel subsets of Euclidean space that is finite on compact sets. (The proof of this is not too hard.)
- However, in ZFC you would have to remove at least one requirement to define a measure on all subsets of Euclidean space as the Vitali set shows. It is a remarkable result due to Robert M. Solovay, that in fact, roughly speaking, it is impossible to construct a nonmeasurable subset of Euclidean space without using the axiom of choice. (The construction of a (nonmeasurable) Vitali set relies on the axiom of choice.) PST 01:35, 7 August 2010 (UTC)
- I shall read that now. Thanks for the link. — Fly by Night (talk) 22:10, 6 August 2010 (UTC)
- You're definitely not going to get any inconsistencies. Just look at the discrete topology on any set - it will satisfy the axioms you listed. It's more likely that these pseudo-topologies turn out to be less interesting/useful/familiar than the standard notion of a topology. You may also be interested by sigma algebra if you've never run into one of those before. J Elliot (talk) 21:01, 6 August 2010 (UTC)
- Thanks for your reply, Tango. It's clear that Euclidean space with a metric topology is an intuitive example of a topology. But I was hoping for something more substantial. For example, are the axioms inconsistent if we drop the finiteness of intersections condition? Etc. — Fly by Night (talk) 20:57, 6 August 2010 (UTC)
- (ec) No, there is nothing inconsistent about them. The trivial and discrete topologies both fit your axioms, just to name two easy examples. Your axioms are more restrictive than the standard ones, so anything satisfying your axioms will satisfy the standard ones. It turns out there are lots of interesting results you can get with just the standard ones, so the standard ones are useful and therefore get used. It is possible there are some results that are only true for spaces satisfying your axioms, in which case yours would be useful too as would also get used. --Tango (talk) 21:03, 6 August 2010 (UTC)
- A pseudotopology is essentially the same thing as a complete lattice. Algebraist 00:43, 7 August 2010 (UTC)
See Alexandrov topology. (I mentioned this above, but I think it is more visible when not indented.) PST 07:13, 7 August 2010 (UTC)
August 7
Solve this equation
FIND THE VALUE OF K IF:9K+12K=16K —Preceding unsigned comment added by 122.170.28.77 (talk) 03:57, 7 August 2010 (UTC)
- A simple bit of iteration. When K=1, the left side is greater. When K=2 the right side is greater. so the answer is somehere between the two. Set lower_limit=1, set upper limit=2, try (lower_limit + upper_limit)/2 and if the result has the left side larger than the right replace the lower_limit by the trial value otherwise replace the upper_limit by the trial value. Repeat until the two sides are equal. -- SGBailey (talk) 05:39, 7 August 2010 (UTC)
- So K ≈ 1.67272093446, but is there an analytic solution? -- 119.31.121.93 (talk) 06:04, 7 August 2010 (UTC)
- There is no need to use iteration. In fact, observe the following easy solution. First write the equation as:
- So K ≈ 1.67272093446, but is there an analytic solution? -- 119.31.121.93 (talk) 06:04, 7 August 2010 (UTC)
- Put and note that the above equation can be rewritten as:
- This is a quadratic equation in x and hence can be solved using the quadratic formula; we obtain:
- (We discard the other solution since is positive for all real k.) Hence:
- Recalling that we obtain that:
- Taking logarithms to the base yields the result:
(edit conflict). If 9K+12K=16K then (9/16)K+(12/16)K=1. Then (3/4)2K+(3/4)K=1. Set x=(3/4)K. Then K=log(x)/log(3/4) and x2+x=1. Then K=log((√5−1)/2))/log(3/4)=(log(√5+1)−log(2))/(2log(2)−log(3)) is an analytic solution. Bo Jacoby (talk) 07:32, 7 August 2010 (UTC).
- So it's log4/3φ. Wonderful!-- 119.31.121.78 (talk) 00:51, 8 August 2010 (UTC)
vectors
Why vector division is not defined? —Preceding unsigned comment added by Mahendrasingh4u (talk • contribs) 05:30, 7 August 2010 (UTC)
- See Quaternion#Algebraic_properties. Bo Jacoby (talk) 07:07, 7 August 2010 (UTC).
- First you would have to define "vector multiplication". Then you would deem "vector division" to be the inverse of this operation. But to even speak of "inverses", you need to define a multiplicative identity of this "vector multiplication" operation. What multiplication operation do you propose that has such a multiplicative identity? (The usual inner product does not work since its output is not a vector but a scalar. The usual cross product does not work either since while it does define a product operation on a set of vectors, it does not have a (non-trivial) multiplicative identity.) PST 07:20, 7 August 2010 (UTC)
- Does the cross product have a trivial identity? The cross product is always perpendicular to the vectors being multiplied and no vector is perpendicular to itself (other than the zero vector, I suppose, depending on the details of your definition). --Tango (talk) 03:32, 8 August 2010 (UTC)
- I probably should have been more clear. The cross product certainly does not have an identity when defined on positive dimensional Eucldiean space. It is conceivable that by deleting some "trivial vectors" one can fix this problem, or put differently, that the problem can be fixed by restricting the cross product to some proper subset of Euclidean space. When I said "non-trivial" identity, I meant that the only vector space in which this problem is totally fixed is the zero-dimensional vector space. But that is, of course, a trivial example. PST 06:38, 8 August 2010 (UTC)
- Does the cross product have a trivial identity? The cross product is always perpendicular to the vectors being multiplied and no vector is perpendicular to itself (other than the zero vector, I suppose, depending on the details of your definition). --Tango (talk) 03:32, 8 August 2010 (UTC)
- First you would have to define "vector multiplication". Then you would deem "vector division" to be the inverse of this operation. But to even speak of "inverses", you need to define a multiplicative identity of this "vector multiplication" operation. What multiplication operation do you propose that has such a multiplicative identity? (The usual inner product does not work since its output is not a vector but a scalar. The usual cross product does not work either since while it does define a product operation on a set of vectors, it does not have a (non-trivial) multiplicative identity.) PST 07:20, 7 August 2010 (UTC)
What is Cr topology and Cr distance in the space of differentiable maps Cr(M,N)
in which the domain (M) and codomain (N) are both manifolds. Thanks for your answer.SongJie@NTU (talk) 14:23, 7 August 2010 (UTC)
- You are refering the the Whitney Ck-topologies, named after Hassler Whitney. There isn't an article on Wikipedia about the Whitney Ck-topologies. They use the differences of partial derivatives to define the distances between mappings. Planetmath has an article, see here— Fly by Night (talk) 18:43, 7 August 2010 (UTC)
- Thanks! that's helpful.SongJie@NTU (talk) 02:52, 8 August 2010 (UTC)
Probability question
I understand this is an incredibly simple problem compared to the questions I have seen posted here, but here goes. I have a bet each week on soccer results. I usually look for odds of around 10/1. I am currently on a losing streak of 50 weeks. I figured I have a 90% chance of losing (ignoring the bookies 1-2% advantage) on any one bet, therefore the odds of this losing streak is 0.9^50 (sorry haven't worked out how to do superscripts) or about 1 in 200. I explained this to a friend who said my logic is flawed. Who is right? Si1965 (talk) 23:11, 7 August 2010 (UTC)
- Why do you think you have a 10% chance of winning any one bet? The odds are set to make money for the bookie, so your chances are probably less than 10%. Maybe a lot less. My chance of getting a date with Keira Knightly is certainly less than 1/1000 (more like zero), and a bookie might give 10-to-1 odds against it, but probably would not give 100-to-1 much less 1000-to-1. 75.62.4.94 (talk) 03:35, 8 August 2010 (UTC)
- The OP already said he was ignoring the bookie's advantage which, as he says, is usually only a few percent. --Tango (talk) 03:42, 8 August 2010 (UTC)
- Well, it's not actually 90%, since it's odds of 10 to 1, not a probability of 1 in 10. See odds. So actually your chance of losing is 10/11 or 91% (the difference is more significant for more likely events, eg. odds of 2/1 against isn't 50%, it's 33%). Otherwise, your logic is fine. Did your friend say what the flaw he saw was? --Tango (talk) 03:37, 8 August 2010 (UTC)
- That said, it is worth pointing out that even a small change in the probability you start with can have a big change in the end result. If we use the correct figure of 91% and then add on 2% for the bookie's advantage (using your numbers, I'm not sure exactly what it usually is) to get 93% then we see that 0.93^50=0.027, which is about 1 in 40. So just a 3% difference has taken us from 1 in 200 to 1 in 40. --Tango (talk) 03:42, 8 August 2010 (UTC)
- Why do you consistently choose to bet on the longshots? Is it because, even though you expect the average results to be the same, you'd rather occasionally win big than regularly win small? See Favourite-longshot bias. You and other longshot favoring bettors may be shifting the odds so that while your bet may pay 10:1, the team's chances of winning may be much less than 1/11. This was discussed recently in WP:Reference desk/Archives/Miscellaneous/2010 August 2#Betting on the ponies -- 119.31.121.72 (talk) 05:44, 8 August 2010 (UTC)
- Note also that although this is the correct way of calculating the probability of this losing streak, i.e. losing in all of these 50 weeks, that's not the same as the probability of ever experiencing a losing streak of 50 weeks or more if you've been betting this way for considerably longer. Calculating that is quite a bit more tricky... --Qwfp (talk) 06:50, 8 August 2010 (UTC)
- A bookie's odds are based on measuring (or estimating) collective public perception, not actual odds. For simplicity, suppose A is playing B. The bookie's goal is to get the amount of money bet on A winning to be equal to the expected payout if B wins and vice versa. In other words, there goal is the ensure that losers pay the winners (after taking a cut for the house, which could either be explicitly expressed, or implicit by not having the total odds sum to unity). Getting the accounts to balance on each side is based on judging how likely people are to bet either side given a specific rate of return, and not on how likely an outcome actually is to occur. Hence it is about perception and willingness to bid, rather than true odds. Collective public wisdom is actually pretty good on average, so the offered odds are often similar to the true odds, but it is subject to biases. One of these is the favourite-longshot bias, which says that people tend to overestimate the odds of longshots winning. Because of this, we can generally expect people to bid on a longshot more often than they should statistically. Bookies know this. In order to get the books to balance, they need to reduce the expected payout for the longshot in order to compensate and make their expected payouts balance. To make a long story short, because people tend to overbid longshots, when a bookie gives 10:1 odds, the true odds might be something more like 25:1. Given true odds of 25:1, we would expect a 50 week losing streak to occur roughly 1 time in 8. Hence, it would be somewhat unlikely, but not a surprising event. Dragons flight (talk) 07:50, 8 August 2010 (UTC)
Thanks to you all for your responses, very interesting and helpful. Si1965 (talk) 09:22, 8 August 2010 (UTC)
Strange notation
The article titled binary logarithm contains this:
Can someone translate this into standard language and notation? Michael Hardy (talk) 23:33, 7 August 2010 (UTC)
- Are you questioning the ⌊⌋, the ⌈⌉, or the >>? Note that n>>1 = ⌊n/2⌋ (and n>>k = ⌊n/2k⌋), and that for these positive n, logical shift and arithmetic shift are equivalent. -- 119.31.121.78 (talk) 01:24, 8 August 2010 (UTC)
- The formula is also incorrect, as shown by evaluating with n=7. I believe that it should read:
- and that it was broken by this edit. -- 112.142.28.242 (talk) 03:47, 8 August 2010 (UTC)
- And, of course, all that it is saying is that the rounded up logarithm is one more than the rounded down logarithm, except for exact powers of two where they are equal. -- 112.142.28.242 (talk) 03:51, 8 August 2010 (UTC)
- I've fixed it. I suspect that the editor who broke it was going for the correct formula:
- which is related to the code snippet that follows in the article. -- 119.31.126.83 (talk) 15:09, 8 August 2010 (UTC)
I was not familiar with the "logical shift" denoted by ">>".
I've changed the word "where" to "if". One writes, for example,
- "p + q
where p is the probability of success", or
- "
where n is the sample size", etc. The word "where" then defines the notation. That's the right way to use "where". Michael Hardy (talk) 16:54, 8 August 2010 (UTC)
- The >> notation comes from the C programming language. It's not really appropriate to use it in a general-mathematics context. --Trovatore (talk) 17:46, 8 August 2010 (UTC)
- I think it's probably okay in that context if a line explaining it is put in. Whatever is done one would need an explanation. Dmcq (talk) 18:53, 8 August 2010 (UTC)
- Surely is both simpler and clearer ? Gandalf61 (talk) 20:10, 8 August 2010 (UTC)
- Depends on wether you consider a binary logarithm a mathematics or computer science concept. Much of the material of this article comers from "Hackers Delight", which is all about low level programming. In that context >> is the correct operation to use as it is a much faster operation than other ways of performing division.--Salix (talk): 21:39, 8 August 2010 (UTC)
- It's still kind of language-specific — C and languages that copied it from C. I suppose it's possible that it's been absorbed into CS generally, but I haven't heard about it. --Trovatore (talk) 21:48, 8 August 2010 (UTC)
- It is not an issue here because >> is no longer used in the article other than in a C code snippet. In my (admittedly dated) experience, we used >> freely in both pseudocode and general formula where appropriate in numerical analysis classes. In such contexts ⌊n/2⌋, while mathematically equivalent, is misleading as it suggests a non-integer division followed by a floor. -- 119.31.121.87 (talk) 23:38, 8 August 2010 (UTC)
- It's still kind of language-specific — C and languages that copied it from C. I suppose it's possible that it's been absorbed into CS generally, but I haven't heard about it. --Trovatore (talk) 21:48, 8 August 2010 (UTC)
- Depends on wether you consider a binary logarithm a mathematics or computer science concept. Much of the material of this article comers from "Hackers Delight", which is all about low level programming. In that context >> is the correct operation to use as it is a much faster operation than other ways of performing division.--Salix (talk): 21:39, 8 August 2010 (UTC)
- Surely is both simpler and clearer ? Gandalf61 (talk) 20:10, 8 August 2010 (UTC)
- I think it's probably okay in that context if a line explaining it is put in. Whatever is done one would need an explanation. Dmcq (talk) 18:53, 8 August 2010 (UTC)
- The >> notation comes from the C programming language. It's not really appropriate to use it in a general-mathematics context. --Trovatore (talk) 17:46, 8 August 2010 (UTC)
August 8
What is Cr norm of the space of maps from X to Y
X and Y are both metric space. Thanks a lot! 155.69.135.100 (talk) 12:26, 8 August 2010 (UTC)
elliptic curves
On page 13 0f "Elliptic Curves" by Dale Husemuller (1986) I read the following: "As for cubics, there is no known method for determining, in a finite number of steps, whether there is a rational point on a given cubic curve. This important question is still open."
My question is whether a method has been found, and if that is the case, where do I find such a method?
amri@vianet.ca --66.225.171.69 (talk) 16:23, 8 August 2010 (UTC)
- I have the second edition, 2004, and it says the same thing. I'm pretty sure it's still true and has to do with the fact that finding the rank of an elliptic curve is very hard. This includes even showing that the rank is 0 being difficult. So, assume so elliptic curve has no points of finite order (which I think is not too hard to determine... but don't quote me on that), then the question is, does it have any points of infinite order. And, if you can't see any obvious ones just by looking at the equation (like clearly y^2 = x^3 - 4x has some solutions you can see without doing any work), then it may be very hard to determine if that elliptic curve has zero points or an infinite number and there is no one method that always works to answer the question. StatisticsMan (talk) 18:31, 8 August 2010 (UTC)
Simple Set Theory
The following discussion is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.
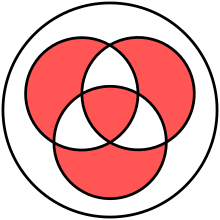
I know that we're lucky to have many talented set theorists on this page, so I'm sure my question will be answered in no time. Given a set X, take two subsets, say A and B, and consider the union A ∪ B and the intersection A ∩ B. For a set C ⊆ A, let A − C = {a ∈ A : a ∉ C}. Let P(X) denote the power set of X. Define a binary operation ƒ : P(X) × P(X) → P(X) given by ƒ(A,B) = (A ∪ B) − (A ∩ B). Notice that this is well defined since A ∩ B ⊆ A ∪ B. Let us write A⋅B in place of ƒ(A,B). I want to show that this binary operation is associative, i.e. for any subsets, A, B and C, of the set X we have (A⋅B)⋅C = A⋅(B⋅C). Explicitly this associativity condition becomes:
- { ( [A ∪ B] − [A ∩ B] ) ∪ C } − { ( [A ∪ B] − [A ∩ B] ) ∩ C } = { A ∪ ( [B ∪ C] − [B ∩ C] ) } − { A ∩ ( [B ∪ C] − [B ∩ C] ) }.
I've done some examples with Venn Diagrams and it seems to be true. The figure that I've included shows (A⋅B)⋅C = A⋅(B⋅C) in red, when A, B and C were solid disks. It doesn't matter which way I do it; I get the same set. I was hoping that someone might be able to help me with the following.
- Does the operation A − C, where C ⊆ A and A − C = {a ∈ A : a ∉ C}, have a name?
- Can we prove formally that (A⋅B)⋅C = A⋅(B⋅C) for all A, B, C ∈ P(X), and if so − how?
I thank you all in advance for what I am sure will be your helpful and well-thought replies. — Fly by Night (talk) 19:53, 8 August 2010 (UTC)
- The first operation is called set difference or set subtraction. Your f is called the symmetric difference. An easy way to see that it's associative is to note that, if you temporarily identify subsets of X with functions from X to {0,1}, where the value is 1 if the element is in the subset and 0 if it isn't, then the symmetric difference corresponds exactly to addition mod 2. --Trovatore (talk) 20:07, 8 August 2010 (UTC)
- Thanks for that, Trovatore. The symmetric difference gives a group operation on P(X). (The identity element is the empty set ∅, and all sets are their own inverses: A⋅A = ∅. Are there any group theoretic results then about P(X)? What about representation theory? (I came up with this idea yesterday while trying to give a group structure to a topology (X,Σ), but that doesn't work because the symmetric difference of open sets need not be open. If you replace Σ – the set of open sets – by P(X) then you're in business). — Fly by Night (talk) 22:10, 8 August 2010 (UTC)
- Well, it's clearly an abelian group. If we consider just finite sets X, then P(X) has a cardinality that is a power of 2, so the classification of finite abelian groups tells us your group is isomorphic to some group (with ). --Tango (talk) 22:31, 8 August 2010 (UTC)
- Thanks for that, Trovatore. The symmetric difference gives a group operation on P(X). (The identity element is the empty set ∅, and all sets are their own inverses: A⋅A = ∅. Are there any group theoretic results then about P(X)? What about representation theory? (I came up with this idea yesterday while trying to give a group structure to a topology (X,Σ), but that doesn't work because the symmetric difference of open sets need not be open. If you replace Σ – the set of open sets – by P(X) then you're in business). — Fly by Night (talk) 22:10, 8 August 2010 (UTC)
- Thanks Tango, but if it's clear – which it is – then there's no point in mentioning it. I was hoping for something interesting and less obvious. For example, do any theorems from group theory translate into non-obvious theorems about set theory, etc. Also, as my reply to Trovatore said: I was trying to give group structures to topologies, so finite sets weren't really what I had in mind. — Fly by Night (talk) 23:18, 8 August 2010 (UTC)
- The point in mentioning it was that the classification theorem I invoked only applies to abelian groups. It's good practice in mathematics to always be explicit about the premises of a theorem being met before invoking the theorem. --Tango (talk) 23:38, 8 August 2010 (UTC)
- True, but irrelevant. You're still no closer to answering my question in a non-trivial way. I appreciate you making the effort to write a reply, but it wasn't really what I was looking for. Thanks again. — Fly by Night (talk) 00:04, 9 August 2010 (UTC)
- Identifying the group has to be the first step in finding out if it can tell you anything useful. --Tango (talk) 00:06, 9 August 2010 (UTC)
- I very much doubt that you will be able to "identify the group". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to learn something new. Better that we leave it here, Tango. Thanks all the same. — Fly by Night (talk) 00:12, 9 August 2010 (UTC)
- Algebraist has identified the group (see below): it's . --Tango (talk) 00:27, 9 August 2010 (UTC)
- Exactly: Algebraist has identified the group. You were talking about finite groups when I had general topologies in mind. That's why I got a frustrated. I apologise for letting things annoy me so easily. — Fly by Night (talk) 22:25, 9 August 2010 (UTC)
- Algebraist has identified the group (see below): it's . --Tango (talk) 00:27, 9 August 2010 (UTC)
- I very much doubt that you will be able to "identify the group". Besides, I was hoping for something more general. Like a theorem in group theory, true for all groups - being translated into the language of set theory. Any way, don't worry. We're obviously not seeing eye to eye on this one. I'm not interested in a tit-for-tat exchange; I was hoping to learn something new. Better that we leave it here, Tango. Thanks all the same. — Fly by Night (talk) 00:12, 9 August 2010 (UTC)
- Identifying the group has to be the first step in finding out if it can tell you anything useful. --Tango (talk) 00:06, 9 August 2010 (UTC)
- True, but irrelevant. You're still no closer to answering my question in a non-trivial way. I appreciate you making the effort to write a reply, but it wasn't really what I was looking for. Thanks again. — Fly by Night (talk) 00:04, 9 August 2010 (UTC)
- The point in mentioning it was that the classification theorem I invoked only applies to abelian groups. It's good practice in mathematics to always be explicit about the premises of a theorem being met before invoking the theorem. --Tango (talk) 23:38, 8 August 2010 (UTC)
- There is an obvious isomorphism between P(X) and the direct product of |X| copies of Z2: just replace sets with their indicator functions, as Trovatore suggested. Algebraist 22:52, 8 August 2010 (UTC)
- Thanks Tango, but if it's clear – which it is – then there's no point in mentioning it. I was hoping for something interesting and less obvious. For example, do any theorems from group theory translate into non-obvious theorems about set theory, etc. Also, as my reply to Trovatore said: I was trying to give group structures to topologies, so finite sets weren't really what I had in mind. — Fly by Night (talk) 23:18, 8 August 2010 (UTC)
- Ah, yes. And that works for infinite X as well, so you've completely identified the group in question for any X. --Tango (talk) 23:15, 8 August 2010 (UTC)
- Here's the thing Algebraist... if it's obvious, then there's no point in mentioning it. StatisticsMan (talk) 02:49, 9 August 2010 (UTC)
- That's not necessarily true. Surely you've seen facts that are "obvious" only after they have been pointed out. —Bkell (talk) 07:21, 9 August 2010 (UTC)
- I know. I am referencing a comment from above by Fly By Night who told Tango he didn't need to point out anything that was clearly true. StatisticsMan (talk) 16:35, 9 August 2010 (UTC)
Thanks to everyone for their answers. I now consider my question to be resolved. Thanks to Trovatore, Tango and Algebraist for their, as ever, insightful comments. I'm also going to archive the thread because I don't think it's moving in such a positive direction. Seeing as the question has been resolved in the OP's eyes, I don't see any problem in archiving. Thanks again to everyone. — Fly by Night (talk) 22:25, 9 August 2010 (UTC)
August 9
Stone-Cech Compactification
Hi, Does anyone have an idea how to calculate the power of the Stone-Cech compactification of a given space X with a given power? Is it 2^X? And if so, how do I show it? Thanks! —Preceding unsigned comment added by Topologia clalit (talk • contribs) 06:17, 9 August 2010 (UTC)
- Certainly not in general. For example βN is the set of ultrafilters on N (with the appropriate topology), so it has cardinality . On the other hand, if X is already compact, then βX is just X (I think). So I don't believe there's a general formula independent of the topology on X. --Trovatore (talk) 06:22, 9 August 2010
(UTC)
Thanks. But can you explain why βN has cardinality ? Why isn't it just ? Topologia clalit (talk) 06:37, 9 August 2010 (UTC)
- Well, on the face of it, an ultrafilter on N is a set of subsets of N, not a subset of N, so you'd kind of expect there to be of them. Of course not every set of subsets of N is an ultrafilter, so this isn't a proof. Nevertheless it's true. It's a theorem of some dude named Pospisil or something like that, with diactritical marks in various places. You can look it up in Jech, Set Theory. --Trovatore (talk) 06:43, 9 August 2010 (UTC)
- Ah, turns out someone had asked about this a long time ago on sci.math, and I wrote up Pospíšil's proof and posted it. You can find it at http://www.math.niu.edu/~rusin/known-math/00_incoming/filters . --Trovatore (talk) 06:48, 9 August 2010 (UTC)
OK Thanks! I'll have a look and try to figure it out. Topologia clalit (talk) 07:12, 9 August 2010 (UTC)
- And of course since you can build the Stone–Čech compactification out of ultrafilters of zero-sets, β of any Tychonoff space X has cardinality at most . Algebraist 09:52, 9 August 2010 (UTC)
- For specific spaces, one can often get a better bound using the same method. For example, there are only zero sets (or even closed sets) in , hence . (In fact, it's easy to see that one can embed βN in βR, hence the cardinality of βR is exactly .)—Emil J. 11:41, 9 August 2010 (UTC)
A question in Topology
Hi, Can anyone see what is the difference between these two definitions?? First definition: A point x is called WFU point if whenever x \in Cl(A)\A thre exists a countable infinite disjpint (CID) family F of finie subsets of A such that for every neighborhood V of x the subfamily {F \in F | F∩V = Ø} is finite. If every point of a space is WFU point, then this space is called WFU -space. Second definition: A point x \in X and a CID familly 'F' of finite subsets of X are said to be in the Reznichenko relation (Rz), written x(Rz)'F', if the following holds:
(Rz) For every neighborhood V of x the subfamily {F \in F | F∩V = Ø}, is finite.
We write x \in A(Rz) if either x \in A or there is a CID family F of finite subsets of A such that x(Rz)'F'. Topologia clalit (talk) 07:03, 9 August 2010
- The first is a property of a point, while the second is a property of a point and a set? In particular, the first says for all with . —Preceding unsigned comment added by 203.97.79.114 (talk) 07:43, 9 August 2010 (UTC)
OK Thanks. I see the difference now. It is just that I'm trying to figure out an example that there exist a countable non-WFU space and I think I keep on missing something here. Here is the example: There exists a countable non-WFU space: Let x be an arbitrary point of the Cech-Stone compactification remainder of the discrete space . Then suppose to be the edesired example. ( X is w union with the set that contains x. X = wU{x}) Of course, it is a countable space. And here is the proof: Let us assume that X is WFU. As , there must be a CID family F such that x(Rz)F. Let A, B be any two infinite subfamilies of F . Then both and must hold. But this is impossiblle if we choose A and B to be disjoint subfamilies of F as in this case and are disjoint subsets of and is an ultrafilter on . The thing which I mostly don't understand in the proof of this example is: How can one be sure that there exists two infinite subfamilies of F? (I Used U as a union, couldn't fugure out how to do it..) Topologia clalit (talk) 08:27, 9 August 2010 (UTC)
- is countable. So number the elements . You can make and . By assumption any open neighborhood of is disjoint from only finitely many of the fs, so if you take , this must hit every open neighborhood of (since it contains infinitely many fs). Similarly . But then and , which is a contradiction, since those are disjoint. (You can make a union using \cup) —Preceding unsigned comment added by 203.97.79.114 (talk) 08:46, 9 August 2010 (UTC)
Thanks!!! Topologia clalit (talk) 08:59, 9 August 2010 (UTC)
Total differential
Good day. As we know, a total differential for
is
but what is the total differential for
? --Merry Rabbit (talk) 14:05, 9 August 2010 (UTC)
- If x, y and t are independent then it is
- On the other hand, if x and y depend on t then it is:
what's wrong with this proof?
What's wrong with this proof? This is not homework. 85.181.49.221 (talk) 21:13, 9 August 2010 (UTC)
P versus NP problem for dummies
OK, I want to understand how this works but I don't actually understand what polynomial time is or all those other bits are. So here's how I think it works and you guys can tell me if I'm right or wrong on the level that I'm working at, which is very low.
Some things are easy to figure out using computers and some things are very hard. Some things are easy to figure out an answer to and easy to prove that an answer is correct for. This is P. On the other hand, some things are easy to prove an answer for but very difficult to figure out an answer to: for example, it's easy to prove that two prime numbers multiply into another number, but it's very tricky to take that number again and figure out the two prime numbers that we started with. These are NP problems. But what the P versus NP problem is is proving that P problems and NP problems are ACTUALLY different and not that we're just stupid and haven't figured out easy ways to do these NP problems yet. Do I have this right? —Preceding unsigned comment added by 88.108.242.37 (talk) 21:50, 9 August 2010 (UTC)
- Almost. The thing you're missing is that all P problems are automatically NP. NP doesn't say that it's hard to figure out the answer; it only says that it's easy to check the answer. NP-complete says it's hard to figure out the answer (or at least as hard as it can be for an NP problem). --Trovatore (talk) 22:16, 9 August 2010 (UTC)
- OK, sweet. 88.108.242.37 (talk) 22:23, 9 August 2010 (UTC)
- ^ Warren Jr., Henry S. (2002), Hacker's Delight, Addison Wesley, pp. pp. 83, ISBN 978-0201914658
{{citation}}:|pages=has extra text (help)



![{\displaystyle [A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79eaa334597b1861f1b08ca0c8fecb3858ebcb12)













![{\displaystyle [\nabla \times {\frac {\mathbf {x} }{r^{3}}}]_{i}=\varepsilon _{ijk}{\frac {\partial }{\partial x_{j}}}{\frac {x_{k}}{r^{3}}}=\varepsilon _{ijk}{\frac {\delta _{jk}}{r^{3}}}-3\varepsilon _{ijk}{\frac {x_{k}}{r^{4}}}{\frac {x_{j}}{r}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6d05cb2dbd1bffeec4aae0a8c3f9fdae0aeb31f)










































































![{\displaystyle x\in [\cup A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3196743d48080a8bfe19c7d1cf9745d7206b5776)
![{\displaystyle x\in [\cup B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3131b6bf38525203378f86d2d96cc65d954b06a4)




