Talk:Constant/Old history: Difference between revisions
Undid revision 171743986 by 75.74.0.121 (talk) |
Randomblue (talk | contribs) |
||
| (460 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
{{otheruses}} |
{{otheruses|constant (disambiguation)}} |
||
In [[mathematics]] and the mathematical [[science]]s, a '''constant''' is a fixed, but possibly unspecified, value. This is in contrast to a [[variable]], which is not fixed. |
|||
'''Constants''' are [[real number|real]] numbers or values which are significantly interesting in some way<ref name="Site 2">{{cite web|url=http://mathworld.wolfram.com/Constant.html|title=Constant|publisher=[[Wolfram MathWorld]]|accessdate=2007-12-09}}</ref>. Constants recur in both [[mathematics]] and [[science]], therefore playing a fundamental role. They may represent universal facts -also called invariants-, link physical quantities within physical theories, check the overall consistency of physical models, simplify notation, or simply be ubiquitous. Constants are very versatile entities as they may be exact or [[approximate]] and [[experimental]]ly determined, [[dimensionless]] or [[dimensional analysis|dimensionful]] with appropriate [[units of measurement]] applied, and even unspecified, when occurring for example in integrals. |
|||
== Unspecified constants == |
|||
When dealing with dimensionfull constants, a set of units must be chosen. Sometimes, one unit is defined in terms of another unit. For example, the [[metre]] is defined as <math>1/(299\ 792\ 458)</math> of a [[Speed of light|light-second]]. This definition implies that, in [[metric unit]]s, the speed of light in vacuum is exactly <math>299\ 792\ 458</math> [[metres per second]]<ref>{{cite web|url=http://physics.nist.gov/cgi-bin/cuu/Value?c |title=Speed of light in vacuum |accessdate=2007-08-08 |author=[[CODATA]]|work=CODATA recommended values |publisher=[[NIST]]}}</ref>. No increase in the [[accuracy and precision|precision]] of the measurement of the speed of light could alter this numerical value expressed in metres per second. |
|||
The most widely mentioned sort of ''constant'' is a fixed, but possibly unspecified [[number]]. For example, consider "''c''" in the [[Pythagorean Theorem]]: ''a''² + ''b''² = ''c''². Here, "''c''" is the [[hypotenuse]] of a right triangle. Though the exact value of "''c''" is unspecified, it always represents the hypotenuse in the Pythagorean Theorem (while ''a'' and ''b'' are interchangeable [as far as the theorem is concerned] and represent the other two sides of the triangle). |
|||
One always talks about [[definable number|definable]], and almost always also, [[computable number|computable]] mathematical constants - [[Chaitin's constant]] being a notable exception. However, there are still some constants -mathematical or not-, like [[Landau's constants]]<ref>{{cite journal|first=Hans|last=Rademacher|authorlink=Hans Rademacher|title=On the Bloch-Landau Constant.|publisher=American Journal of Mathematics|volume=65|pages=387-390|date=1943|accessdate=2007-12-09}}</ref>, [[Erdos' reciprocal sum constants]]<ref>{{cite book|last=Finch|first=Steven|year=2003|title=Mathematical constants|publisher=[[Cambridge University Press]]|page=163|id=ISBN 0-521-81805-3}}</ref> or the [[Fermi coupling constant]] for which only very rough estimates are known. |
|||
Usually the term ''constant'' is used in connection with mathematical [[function (mathematics)|function]]s of one or more [[variable]] [[parameter]]s. These parameters, or other variables, are often called ''x'', ''y'', or ''z'', using lowercase letters from the end of the [[Latin alphabet]]. Constants are, by convention, usually denoted by lowercase letters from the beginning of the Latin alphabet, such as ''a'', ''b'', and ''c''. |
|||
As noted by [[Steven Finch]], "All numbers are not created equal." <ref>{{cite book|last=Finch|first=Steven|year=2003|title=Mathematical constants|publisher=[[Cambridge University Press]]|id=ISBN 0-521-81805-3}}</ref> We shall therefore make the following classification: 'super-universal' constants -those appearing in different parts of science-, universal constants in a certain domain, and the more specific constants: mathematical curiosities, specific physical facts and unspecified constants. |
|||
== Specified constants == |
|||
=== 'Super-universal' constants - occurring in different parts of science === |
|||
Of course, some constants have special symbols, because they ''are'' specified, such as {{num|1}} or [[pi|π]]. A special case of this may be found in [[physics]], [[chemistry]], and related fields, where certain features of the natural world that are described by numbers are found to have the same value at all times and places. |
|||
Ubiquitous in many different fields of science, such recurring constants include [[pi|<math>\pi</math>]], [[e (mathematical constant)|<math>e</math>]] and the [[Feigenbaum constants]] which are linked to the [[mathematical model]]s used to describe physical phenomena, [[Euclidian geometry]], [[mathematical analysis|analysis]] and [[logistic map]]s respectively. However, mathematical constants such as [[Apéry's constant]] and the [[Golden ratio]] occur unexpectedly outside of mathematics. |
|||
For example, in [[Albert Einstein]]'s [[special theory of relativity]], we have the [[mass-energy equivalence]] [[formula]] |
|||
==== Archimedes' constant <math>\pi</math> ==== |
|||
:''E'' = ''mc''². |
|||
[[Image:Pi-unrolled-720.gif|thumb|220px|left|The circumference of a circle with diameter 1 is <math>\pi</math>.]] |
|||
Here, the letter ''c'' stands for the [[speed of light]] in a [[vacuum]], a constant [[physical quantity]] which is the same in all physical situations (to the best of current knowledge). |
|||
[[Pi]], though having a natural [[definition]] in [[Euclidian geometry]] (the [[circumference]] of a [[circle]] of [[diameter]] 1), may be found in many different places in mathematics. Key examples include the [[Gaussian integral]] in [[complex analysis]], n<sup>th</sup> [[roots of unity]] in [[number theory]] and [[Cauchy distribution]]s in [[probability]]. However, its universality is not limited to mathematics. Indeed, various formulas in physics, such as [[Heisenberg's uncertainty principle]], and constants such as the [[cosmological constant]] bear the constant pi. The presence of pi in physical [[principles]], [[law (principle)|laws]] and [[formula]]s can have very simple explanations. For example, [[Coulomb's law]], describing the inverse square proportionality of the [[magnitude]] of the [[electrostatic force]] between two [[electric charge]]s and their distance, states that, in [[SI units]], <math> F = \frac{1}{4\pi\varepsilon_0}\frac{\left|q_1 q_2\right|}{r^2}</math><ref>{{cite web|url=http://mathworld.wolfram.com/Sphere.html|title=Sphere|publisher=[[Wolfram MathWorld]]}}</ref>. |
|||
In contrast, the letter ''m'' stands for the [[mass]] of an object, which could be anything, so it is a variable. |
|||
''E'' stands for the object's rest [[energy]], another variable, and the formula defines a [[function (mathematics)|function]] that gives rest energy in terms of mass. |
|||
==== The exponential growth - or Napier's - constant <math>e</math> ==== |
|||
In computer science, a specified constant is sometimes called an '''immediate'''. Immediates are simply a number, rather than a symbol. For example, in the phrase <code>x=45</code>, "45" is an immediate, while "x" is a variable that is assigned the constant value 45. |
|||
[[Image:Exponential.png|thumb|180px|right|Exponential growth (green) describes many physical phenomena.]] |
|||
== Constant term == |
|||
[[Image:Universe_Expansion_Timeline_(fr).png|thumb|180px|left|The expansion of the universe is described using exponentials.]] |
|||
The [[exponential growth]] constant appears in many parts of applied mathematics. For example, as the [[Swiss]] mathematician [[Jacob Bernoulli]] discovered, e arises in [[compound interest]]. Indeed, an account that starts at $1, and yields <math>1+R\,</math> dollars at simple interest, will yield <math>e^R\,</math> dollars with continuous compounding. <math>e</math> also has applications to [[probability theory]], where it arises in a way not obviously related to exponential growth. Suppose that a gambler plays a slot machine with a one in n probability and plays it n times. Then, for large n (such as a million) the [[probability]] that the gambler will win nothing at all is (approximately) <math>1/e\,</math>. Another application of e, also discovered in part by Jacob Bernoulli along with [[French]] mathematician [[Pierre Raymond de Montmort]] is in the problem of [[derangement]]s, also known as the ''hat check problem''<ref>{{cite web|url=http://www.dartmouth.edu/~chance/teaching_aids/books_articles/probability_book/book.html|title=Introduction to probability theory|authors=Grinstead, C.M. and Snell, J.L.|licence=[[GFDL]]|page=85|accessdate=2007-12-09}}</ref>. Here ''n'' guests are invited to a party, and at the door each guest checks his hat with the butler who then places them into labelled boxes. But the butler does not know the name of the guests, and so must put them into boxes selected at random. The problem of de Montmort is: what is the probability that ''none'' of the hats gets put into the right box. The answer is <math>p_n = 1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\cdots+(-1)^n\frac{1}{n!}</math> and as the number <math>n\,</math> of guests tends to infinity, <math>p_n\,</math> approaches <math>1/e\,</math>. |
|||
A ''constant term'' is a number that appears as an [[addend]] in a [[formula]], such as |
|||
:<math>f(x) = \sin x + c.</math> |
|||
Here the constant ''c'' is the constant term of the [[function (mathematics)|function]] ''f''. |
|||
The value of ''c'' has not been specified in this formula, but it must be a specific value for ''f'' to be a specific function. |
|||
==== The Feigenbaum constants <math>\alpha</math> and <math>\delta</math> ==== |
|||
The constant term may depend on how the formula is written. For example |
|||
:<math>f(x) = x^3+(\sin x)^2 + 4</math> |
|||
and |
|||
:<math>g(x) = x^3-(\cos x)^2 + 5</math> |
|||
are formulae for the same function. |
|||
[[Image:LogisticMap BifurcationDiagram.png|thumb|200px|left|Bifurcation diagram of the logistic map]] |
|||
In a [[polynomial]] (or a generalisation of a polynomial, such as a [[Taylor series]] or [[Fourier expansion]]), the constant term is associated to the [[exponent]] [[0 (number)|zero]]. |
|||
Note that the constant term may be zero, however. |
|||
In a sense, any formula has a constant term, if you allow the constant term to be zero. |
|||
Iterations of continuous maps serve as the simplest examples of models for dynamical systems.<ref>{{cite book|author=Collet & Eckmann|year=1980|title=Iterated maps on the inerval as dynamical systems|publisher=Birkhauser|id=ISBN 3-7643-3026-0}}</ref> The two [[Feigenbaum constants]] appear in such iterative processes: they are mathematical invariants of [[logistic map]]s with quadratic maximum points<ref>{{cite book|last=Finch|first=Steven|year=2003|title=Mathematical constants|publisher=[[Cambridge University Press]]|page=67|id=ISBN 0-521-81805-3}}</ref> and their [[bifurcation diagram]]s. |
|||
For some purposes, the constant is taken to be the value of ''f''(0), but this depends on the function being defined at 0; it would not work for ''f''(''x'')=1-1/''x''. |
|||
The logistic map is a [[polynomial]] mapping, often cited as an archetypal example of how [[chaos theory|chaotic]] behaviour can arise from very simple [[non-linear]] dynamical equations. The map was popularized in a seminal [[1976]] paper by the [[English]] biologist [[Robert May, Baron May of Oxford|Robert May]]<ref>{{cite book|first=Robert|last=May|authorlink=Robert May, Baron May of Oxford|date=1976|title=Theoretical Ecology: Principles and Applications|publisher=Blackwell Scientific Publishers|id=ISBN 0-632-00768-0}}</ref>, in part as a discrete-time demographic model analogous to the logistic equation first created by [[Pierre François Verhulst]]. The difference equation is intended to capture the two effects or reproduction and starvation. |
|||
==== Apéry's constant <math>\zeta(3)</math> ==== |
|||
[[Image:Apéry's constant.png|right]] |
|||
Despite being a special value of the [[Riemann zeta function]], [[Apéry's constant]] arises naturally in a number of physical problems, including in the second- and third-order terms of the [[electron]]'s [[gyromagnetic ratio]], computed using [[quantum electrodynamics]]<ref>{{cite web|url=http://mathworld.wolfram.com/AperysConstant.html|title=Apéry's constant|first=Steven|last=Finch|accessdate=2007-12-08}}</ref>. Also, [[Pascal Wallish]] noted that <math>\sqrt{m_n/m_e}\approxeq\frac{3}{\sqrt{\varphi}-\zeta(3)}</math><ref>{{cite web|url=http://www.eaglemanfoundation.org|title=The Eagleman Prize in Mathematics and Physics}}</ref>, where <math>m_n,m_e,\varphi</math> are the [[neutron]] mass, the [[electron]] mass and the [[Golden ratio]] respectively. |
|||
==== The Golden ratio <math>\varphi</math> ==== |
|||
[[Image:Icosahedron-golden-rectangles.svg|thumb|right|Golden rectangles in an icosahedron]] |
|||
<div class="thumb tleft"> |
|||
<div class="thumbinner" style="width:260px;"><math>F\left(n\right)=\frac{\varphi^n-(1-\varphi)^n}{\sqrt 5}</math> |
|||
<div class="thumbcaption">An explicit formula for the n<sup>th</sup> [[Fibonacci number]] involving the [[Golden ratio]].</div></div></div> |
|||
The number <math>\varphi</math> turns up frequently in [[geometry]], particularly in figures with pentagonal [[symmetry]]. Indeed, the length of a regular [[pentagon]]'s [[diagonal]] is <math>\varphi</math> times its side. The vertices of a regular [[icosahedron]] are those of [[three]] mutually [[orthogonal]] [[golden rectangle]]s. Also, it appears in the [[Fibonacci sequence]], related to growth by [[recursion]]<ref>{{cite book|last=Livio|first=Mario|authorlink=Mario Livio|year=2002|title=The Golden Ratio: The Story of Phi, The World's Most Astonishing Number|publisher=Broadway Books|location=New York|id=ISBN 0-7679-0815-5}}</ref>. |
|||
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the [[stem]]s of plants and of [[vein]]s in leaves. He extended his research to the [[skeleton]]s of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of [[crystal]]s, even to the use of proportion in artistic endeavours. In these phenomena he saw the golden ratio operating as a universal law.<ref>{{cite journal|journal=Nexus Network Journal|first=Richard|last=Padovan|title=Proportion: Science, Philosophy, Architecture|volume=4|number=1|pages=113-122|doi=10.1007/s00004-001-0008-7}}</ref> Zeising wrote in 1854: |
|||
<blockquote>[The Golden Ratio is a universal law] in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all [[structure]]s, [[form]]s and [[proportion]]s, whether cosmic or individual, [[organic]] or [[inorganic]], [[acoustic]] or [[optical]]; which finds its fullest realization, however, in the human form.<ref>{{cite book|first=Adolf|last=Zeising|title=Neue Lehre van den Proportionen des meschlischen Körpers|date=1854|page=preface}}</ref></blockquote> |
|||
=== Universal constants - occurring in general mathematical settings or physical phenomena === |
|||
In mathematics, these constants are invariants of wide classes of objects. For example, <math>\pi</math> is the invariant [[ratio]] of any [[circle]]'s [[circumference]] to its [[diameter]]<ref>{{cite web|url=http://mathforum.org/dr.math/faq/faq.pi.html|title=About Pi|work=Ask Dr. Math FAQ|accessdate=2007-11-27}}</ref>. It is in specific mathematical settings that such natural definitions arise. For example, [[Catalan's constant]] in [[combinatorics]], [[Euler-Mascheroni constant]] in [[analysis]], etc. In physics, universal constants appear in the basic theoretical equations upon which the entire science rests or are the properties of the fundamental particles of physics of which all matter is constituted (the [[electron charge]] <math>e</math>, the [[electron mass]] <math>m_e</math> and the [[fine-structure constant]] <math>\alpha</math>). |
|||
==== The Euler-Mascheroni constant <math>\gamma</math> ==== |
|||
[[Image:Euler-Mascheroni.jpg|thumb|180px|right|The area between the two curves (red) tends to a limit.]] |
|||
The [[Euler-Mascheroni constant]] is a recurring constant in [[number theory]]. The [[French]] mathematician [[De la Vallée Poussin]] proved in 1898 that when taking any positive integer n and dividing it by each positive integer m less than n, the [[average]] fraction by which the quotient n/m falls short of the next integer tends to <math>\gamma</math> as n tends to [[infinity]]. Surprisingly, this average doesn't tend to one half<ref>{{cite web|url=http://www.mathcad.com/library/Constants/euler.htm|title=Euler-Mascheroni constant|first=Steven|last=Finch|publisher=Mathcad|accessdate=2007-12-08}}</ref>. |
|||
The Euler-Mascheroni constant also appears in [[Mertens' theorems|Merten's third theorem]] and has relations to the [[gamma function]], the [[zeta function]] and many different integrals and [[series]]. |
|||
The definition of the Euler-Mascheroni constant exhibits a close link between the [[discrete]] and the [[continuous]] (see curves on the right). |
|||
==== Conway's constant <math>\lambda</math> ==== |
|||
<div class="thumb tleft"> |
|||
<div class="thumbinner" style="width:80px;"><math>\begin{matrix} 1 \\ 11 \\ 21 \\ 1211 \\ 111221 \\ 312211 \\ \vdots \end{matrix}</math> |
|||
<div class="thumbcaption">[[Conway]]'s [[look-and-say sequence]]</div></div></div> |
|||
[[Conway's constant]] is the invariant growth rate of all [[derived string]]s similar to the [[look-and-say sequence]] (except two trivial ones)<ref>{{cite book|last=Finch|first=Steven|year=2003|title=Mathematical constants|publisher=[[Cambridge University Press]]|page=453|id=ISBN 0-521-81805-3}}</ref>. |
|||
It is given by the unique positive real root of a [[polynomial]] of degree 71 with integer coefficients<ref>{{cite web|url=http://mathworld.wolfram.com/ConwaysConstant.html|first=Steven|last=Finch|title=Conway's Constant|publisher=[[Wolfram MathWorld]]|accessdate=2007-12-07}}</ref>. |
|||
==== Khinchin's constant <math>K</math> ==== |
|||
If a real number <math>r\,</math> is written using [[simple continued fraction]] <math>r=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\dots}}}</math>, then, as [[Russian]] mathematician [[Khinchin]] proved in 1934, the [[limit of a sequence|limit]] as <math>n\,</math> tends to [[infinity]] of the [[geometric mean]] <math>(a_1a_2\dots a_n)^{1/n}</math> exists, and, except for a set of [[measure (mathematics)|measure]] 0, this limit is a constant, [[Khinchin's constant]]<ref>{{cite book|first=Kac|title=M. Statistical Independence in Probability, Analysis and Number Theory|publisher=Mathematical Association of America|date=1959}}</ref><ref>{{cite web|url=http://mathworld.wolfram.com/KhinchinsConstant.html|title=Khinchin's Constant|first=Steven|last=Finch|publisher=[[Wolfram MathWorld]]|accessdate=2007-12-08}}</ref>. |
|||
==== The speed of light <math>c</math> and Planck's constant <math>h</math> ==== |
|||
The [[velocity of light]] and [[Planck's constant]] are examples of [[quantity|quantities]] that occur naturally in the mathematical formulation of certain fundamental physical theories, the former in [[James Clerk Maxwell]]'s theory of [[electric field|electric]] and [[magnetic field]]s and [[Albert Einstein]]'s theories of relativity, and the latter in quantum theory. For example, in [[special relativity]], mass and energy are equivalent: [[mass-energy equivalence|<math>E=mc^2\,</math>]]<ref>{{Citation |first=Albert|last=Einstein|authorlink=Albert Einstein|year=1905|title=Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?|url=http://www.physik.uni-augsburg.de/annalen/history/papers/1905_18_639-641.pdf|journal=Annalen der Physik|volume =18|pages =639–643|accessdate=2007-12-09}} See also the [http://www.fourmilab.ch/etexts/einstein/specrel/www english translation].</ref> where <math>c^2\,</math> is the constant of proportionality. In [[quantum mechanics]], the energy and [[frequency]] of a photon are related by <math>E=h\nu\,</math>. |
|||
The speed of light is also used to express other fundamental constants <ref>{{cite web|url=http://physics.nist.gov/cgi-bin/cuu/Category?view=html&Universal.x=15&Universal.y=6 |title=Values of the Fundamental Constants|accessdate=2007-12-09|author=[[CODATA]]|work=CODATA recommended values|publisher=[[NIST]]}}</ref> such as the [[electric constant]] <math>\epsilon_0=(4\pi 10^{-7} c^2)^{-1}\,</math>, [[Coulomb's constant]] <math>k=10^{-7} c^2\,</math> and the [[characteristic impedance of vacuum]] <math>Z_0=4\pi10^{-7}c\,</math>. |
|||
==== The electron charge <math>e</math> and the electron mass <math>m_e</math> ==== |
|||
The [[electron charge]] and the [[electron mass]] are examples of constants that characterize the basic, or elementary, [[particle]]s that constitute matter, such as the [[electron]], [[alpha particle]], [[proton]], [[neutron]], [[muon]], and [[pion]]<ref>{{cite book|title=[[Encyclopaedia Britannica]]|article=Physical Constants|volume=5|page=75|edition=15|publisher=Helen Hemingway Benton|date=1974|ISBN=0-85229-290-2}}</ref>. Many constants can be expressed using the fundamental constants <math>h,\,c,\,e</math>. For example. it is a property of a [[supercurrent]] (superconducting electrical current) that the [[magnetic flux]] passing through any area bounded by such a current is [[quantum|quantized]]. The [[magnetic flux quantum]] <math>\Phi_0=hc/(2e)\,</math> is a physical constant, as it is independent of the underlying material as long as it is a [[superconductor]]. Also, the fundamental [[fine-structure constant]] <math>\alpha=\mu_0ce^2/(2h)\,</math> where the [[permeability of free space]] <math>\mu_0</math> is just a numerical constant equal to <math>4\pi\times 10^{-7}</math>. |
|||
=== Mathematical curiosities, specific physical facts and unspecified constants === |
|||
==== Simple representatives of sets of numbers ==== |
|||
[[Image:Ybc7289-bw.jpg|left|thumb|160px|This [[Babylonian]] clay tablet gives an approximation of <math>\sqrt{2}</math> in four [[sexagesimal]] figures, which is about six [[decimal]] figures <ref>{{cite journal|last=Fowler|first=David|authorlink=David Fowler (mathematician)|coauthors=[[Eleanor Robson]]|year=1998|month=November|title=Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context|journal=Historia Mathematica|volume=25|issue=4 |pages=368|url=http://www.hps.cam.ac.uk/dept/robson-fowler-square.pdf|accessdate=2007-12-09}}<br>[http://it.stlawu.edu/%7Edmelvill/mesomath/tablets/YBC7289.html Photograph, illustration, and description of the ''root(2)'' tablet from the Yale Babylonian Collection]<br>[http://www.math.ubc.ca/%7Ecass/Euclid/ybc/ybc.html High resolution photographs, descriptions, and analysis of the ''root(2)'' tablet (YBC 7289) from the Yale Babylonian Collection]</ref>.]] |
|||
<div class="thumb tright"> |
|||
<div class="thumbinner" style="width:460px;"><math>c=\sum_{j=1}^\infty 10^{-j!}=0.\underbrace{\overbrace{110001}^{3!\,digits}000000000000000001}_{4!\,digits}000\dots\,</math> |
|||
<div class="thumbcaption">[[Liouville's constant]] is a simple example of a [[transcendental number]].</div></div></div> |
|||
Some constants, such as the [[square root of two]], [[Liouville's constant|Liouville's constant]] and [[Champernowne constant|Champernowne constant <math>C_{10} = \color{black}0.\color{blue}1\color{black}2\color{blue}3\color{black}4\color{blue}5\color{black}6\color{blue}7\color{black}8\color{blue}9\color{black}10\color{blue}11\color{black}12\color{blue}13\color{black}14\color{blue}15\color{black}16\dots</math>]] are not important mathematical invariants but retain interest being simple representatives of special sets of numbers, the [[irrational number]]s<ref>{{cite web|url=http://www.cut-the-knot.org/proofs/sq_root.shtml|title=Square root of 2 is irrational|first=Alexander|last=Bogomolny}}</ref>, the [[transcendental number]]s<ref>{{cite journal|title=On Transcendental Numbers|author=Aubrey J. Kempner|journal=Transactions of the American Mathematical Society|volume=17|issue=4|year=Oct 1916|pages=476-482}}</ref> and the [[normal number]]s (in base 10)<ref>{{cite journal|title=The onstruction of decimals normal in the scale of ten|first=david|last=Champernowne|authorlink=D. G. Champernowne|journal=Journal of the London Mathematical Society|volume=8|year=1933|pages=254-260}}</ref> respectively. The discovery of the [[irrational number]]s is usually attributed to the [[Pythagorean]] [[Hippasus of Metapontum]] who proved, most likely geometrically, the irrationality of <math>\sqrt{2}</math> and Liouville's constant, named after [[French]] mathematician [[Joseph Liouville]], was the first transcendental number ever constructed<ref>{{cite web|url=http://mathworld.wolfram.com/LiouvillesConstant.html|title=Liouville's Constant|publisher=[[Wolfram MathWorld]]|accessdate=2007-12-09}}</ref>. |
|||
==== Chaitin's constant <math>\Omega</math> ==== |
|||
In the [[computer science]] subfield of [[algorithmic information theory]], [[Chaitin's constant]] is the real number representing the [[probability]] that a randomly-chosen [[Turing machine]] will halt, formed from a construction due to [[Argentine]]-[[American]] mathematician and [[computer scientist]] [[Gregory Chaitin]]. Amusingly, [[Chaitin's constant]], though not being [[computable]], it has been proven [[transcendental]] and [[normal]]. |
|||
{| class="wikitable" align="right" border="1" cellpadding="2" cellspacing="0" style="margin:0 0 0.5em 0.5em" |
|||
{{Elementbox_section_physicalprop | color1=#ffc0c0 | color2=black }} |
|||
{{Elementbox_density_gpcm3nrt | 19.3 }} |
|||
{{Elementbox_densityliq_gpcm3mp | 17.31 }} |
|||
{{Elementbox_meltingpoint | k=1337.33 | c=1064.18 | f=1947.52 }} |
|||
{{Elementbox_boilingpoint | k=3129 | c=2856 | f=5173 }} |
|||
{{Elementbox_heatfusion_kjpmol | 12.55 }} |
|||
{{Elementbox_heatvaporiz_kjpmol | 324 }} |
|||
{{Elementbox_heatcapacity_jpmolkat25 | 25.418 }} |
|||
{{Elementbox_footer | color1=#ffc0c0 | color2=black }} |
|||
==== Constants representing physical properties of elements ==== |
|||
Such constants represents characteristics of certain physical objects such as the [[chemical element]]s. Examples include [[density]], [[melting point]] and [[heat of fusion]]. Some of the properties of [[gold]] are listed in the box on the right. |
|||
==== Unspecified constants ==== |
|||
When unspecified, constants indicate classes of similar objects, commonly functions, all equal up to a constant - or, technically speaking, similarity up to a constant. Such constants appear frequently when dealing with [[integral]]s and [[differential equation]]s. Though unspecified, they have a specific value, which often isn't important. |
|||
[[Image:Different constants of integration.jpg|thumb|200px|left| Solutions with different constants of integration of <math>y'(x)=-2y+e^{-x}\,</math>.]] |
|||
===== In integrals ===== |
|||
[[Indefinite integral]]s are called indefinite because their solutions are only unique only up to a constant. For example, when working over the [[field (mathematics)|field]] of real numbers <math>\int\cos x\ dx=\sin x+C</math> where <math>C\,</math>, the [[constant of integration]], is an arbitrary fixed real number<ref>{{cite book|title=Calculus with analytic geometry|first=Henry|last=Edwards|author=Henry Edwards|coauthors=David Penney|edition=4e|page=269|publisher=Prentice Hall|id= ISBN 0-13-300575-5}}</ref>. In other words, whatever the value of <math>C\,</math>, [[differential|differentiating]] <math>\sin x+C\,</math> with respect to <math>x\,</math> always yields <math>\cos x\,</math>. |
|||
===== In differential equations ===== |
|||
In a similar fashion, constants appear in the [[solution]]s to differential equations where not enough [[initial value]]s or [[boundary condition]]s are given. For example, the [[ordinary differential equation]] <math>y'(x)=y(x)\,</math> has solution <math>Ce^x\,</math> where <math>C\,</math> is an arbitrary constant. |
|||
When dealing with [[partial differential equations]], the constants may be [[constant function|functions]], '''constant with respect to''' some variables (but not necessarily all of them). For example, the [[PDE]] <math>\frac{\partial f(x,y)}{\partial x}=0</math> has solutions <math>f(x,y)=C(y)\,</math> where <math>C(y)\,</math> is an arbitrary function in the [[variable]] <math>y\,</math>. |
|||
=== Notation === |
|||
==== Representing constants ==== |
|||
Different [[symbol]]s are used to represent and manipulate constants, such as <math>1\,</math>, <math>\pi\,</math> and <math>\epsilon_0\,</math>. It is common, in both mathematics and physics, to express the numerical value of a constant by giving its [[decimal expansion]]. For two reasons this representation may cause problems. First, even though rational numbers all have a finite or ever-repeating decimal expansion, some numbers don't have such an expression and it would hence be impossible to completely give its value using this method. Also, the decimal expansion of a number is not necessarily unique. For example, the numbers [[0.999...]] and 1 are equivalent<ref>{{cite book|last=Rudin |first=Walter |authorlink=Walter Rudin |title=Principles of mathematical analysis |edition=3e |year=1976 |origyear=1953 |publisher=McGraw-Hill |id=ISBN 0-07-054235-X|page=61 |theorem=3.26}}</ref><ref>{{cite book|last=Stewart|first=James|authorlink=James Stewart (mathematician)|title=Calculus: Early transcendentals|edition=4e|year=1999|publisher=Brooks/Cole|id=ISBN 0-534-36298-2|page=706}}</ref>, that is they represent the same constant. |
|||
Note that finding the decimal expansions of constants has often been of interest to many people. Some of the mathematical constant, such as <math>\pi,\,e,\,\sqrt{2}</math> have over <math>10^{11}\,</math> (one hundred billion) known digits and very fast [[algorithm]]s, as for [[Apéry's constant]], have being constructed. In physics, it is important to know the numerical values of the fundamental constants with high accuracy for at least two reasons, the first to achieve accurate quantitative descriptions of the physical universe and the second to test the overall consistency and correctness of the basic theories of physics. |
|||
<div class="thumb tright"> |
|||
<div class="thumbinner" style="width:260px;"><math>G=\left . \begin{matrix} 3 \underbrace{ \uparrow \ldots \uparrow } 3 \\ \underbrace{\vdots } \\ 3 \uparrow\uparrow\uparrow\uparrow 3 \end{matrix} \right \} \text{64 layers}</math> |
|||
<div class="thumbcaption">[[Graham's number]] defined using [[up-arrow notation]].</div></div></div> |
|||
It happens that some constants differ so much from the usual kind that a special notation must be invented to represent them. [[Graham's number]] is such an example when the [[Knuth up-arrow notation]] is used<ref>{{cite journal|journal=Science|last=Knuth|first=Donald|authorlink=Donald Knuth|title=Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations.|volume=194|pages=1235-1242|date=1976}}</ref><ref name="Site 1">{{cite web|url=http://www.po28.dial.pipex.com/maths/constant.htm|title=mathematical constants|accessdate=2007-11-27}}</ref>. |
|||
Commonly, constants in the physical sciences are represented using the [[scientific notation]], with, when appropriate, the inaccuracy - or [[measurement error]] - attached. When writing [[Planck's constant]] <math>h=6.626\ 068\ 96(33) \times 10^{-34}\ \mbox{J}\cdot\mbox{s}</math><ref>{{cite web|url=http://physics.nist.gov/cgi-bin/cuu/Value?h |title=Planck constant|accessdate=2007-12-09|author=[[CODATA]]|work=CODATA recommended values|publisher=[[NIST]]}}</ref> it is meant that <math>h=(6.626\ 068\ 96 \plusmn 0.000\ 000\ 003\ 3)\times 10^{-34}\ \mbox{J}\cdot\mbox{s}\,</math>. Only the [[significant figures]] are shown and a greater [[precision]] would be superfluous, extra figures coming from experimental inaccuracies. When writing [[Isaac Newton]]'s [[gravitational constant]] <math>G = \left(6.67428 \plusmn 0.00067 \right) \times 10^{-11} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2} \,</math><ref>{{cite web|url=http://www.physics.nist.gov/cgi-bin/cuu/Value?bg |title=Newtonian constant of gravitation|accessdate=2007-12-09 |author=[[CODATA]]|work=CODATA recommended values|publisher=[[NIST]]}}</ref> only 6 significant figures are given. |
|||
For mathematical constants, it may be of interest to represent them using [[Mathematical constants (sorted by continued fraction representation)|continued fraction]]s to perform various studies, including statistical analysis. Many mathematical constants have an [[analytic form]], that is they can constructed using well-known operations that lend themselves readily to calculation. However, [[Grossman's constant]] has no known analytic form<ref>{{cite web|url=http://mathworld.wolfram.com/GrossmansConstant.html|title=Grossman's constant|first=Steven|last=Finch|accessdate=2007-12-09}}</ref>. |
|||
==== Symbolizing and naming of constants ==== |
|||
Symbolizing constants with letters is a frequent means of making the [[notation]] more concise. A standard [[Convention (norm)|convention]], instigated by [[Euler]] is the 18th century, is to use [[lowercase]] letters from the beginning of the [[Latin alphabet]] <math>a,b,c,\dots\,</math> or the [[Greek alphabet]] <math>\alpha,\beta,\,\gamma,\dots\,</math> when dealing with constants in general. |
|||
<div class="thumb tright"> |
|||
<div class="thumbinner" style="width:220px;">[[Erdős–Borwein constant]] <math>E_B\,</math><br />[[Embree-Trefethen constant]] <math>\beta*\,</math><br />[[Brun's constant]] for [[twin prime]] <math>B_2\,</math><br />[[Rydberg constant]] <math>R_\infty</math><br />[[cardinal number]] [[aleph naught|aleph naught <math>\aleph_0</math>]] |
|||
<div class="thumbcaption">Different kinds of notation.</div></div></div> |
|||
However, for more important constants, the symbols may be more complex and have an extra letter, an [[asterisk]], a number, a [[lemniscate]] or use different alphabets such as [[Hebrew alphabet|Hebrew]], [[Cyrillic alphabet|Cyrillic]] or [[Gothic alphabet|Gothic]]<ref name="Site 1"/>. |
|||
<div class="thumb tleft"> |
|||
<div class="thumbinner" style="width:420px;"><math>googol=10^{100}\,\ ,\ googolplex=10^{googol}=10^{10^{100}}\,</math> |
|||
</div></div> |
|||
Sometimes, the symbol representing a constant is a whole word. For example, [[United States|American]] mathematician [[Edward Kasner]]'s 9-year-old nephew coined the names [[googol]] and [[googolplex]]<ref>{{cite book|authors=Edward Kasner and James R. Newman|title=Mathematics and the Imagination|publisher=[[Microsoft Press]]|year=1989|page=23}}</ref><ref name="Site 1"/> |
|||
[[Image:Parabolic constant illustration v4.svg|thumb|right|180px|The [[parabolic constant]] is the ratio of the [[arc length]] of the parabolic segment formed by the [[latus rectum]] (red) to its [[focal parameter]] (green).]] |
|||
The names are either related to the meaning of the constant ([[parabolic constant]], [[characteristic impedance of vacuum]], [[twin prime constant]], [[electric constant]], [[conductance quantum]], ...), to a specific person ([[Planck's constant]], [[Sierpiński's constant]], [[Dirac's constant]], [[Josephson constant]], ...) or both ([[Gravitational constant|Newtonian constant of gravitation]], [[Bohr magneton]], [[Fermi coupling constant]]<ref>{{cite web|url=http://physics.nist.gov/cgi-bin/cuu/Value?gf |title=Fermi coupling constant|accessdate=2007-12-09 |author=[[CODATA]]|work=CODATA recommended values|publisher=[[NIST]]}}</ref>,...). |
|||
==== Lumping constants ==== |
|||
A common practice in physics is to [[constant lumping|lump constants]], to simply the equations and algebraic manipulations. For example, [[Coulomb's constant]] <math>\kappa =(4\pi\epsilon_0)^{-1}\,</math><ref>{{cite web|url=http://scienceworld.wolfram.com/physics/CoulombsConstant.html|title=Coulomb's constant|publisher=Wolfram World of Physics|accessdate=2007-12-09}}</ref> is just <math>\epsilon_0\,</math>, <math>\pi\,</math> and <math>4\,</math> lumped together. Also, combining old constants does not necessarily make the new one less fundamental. For example, the -notably- dimensionless [[fine-structure constant]] <math>\alpha=\mu_0ce^2/(2h)\,</math> is a fundamental constant of quantum electrodynamics and in the quantum theory of the interaction among [[electron]]s, [[muon]]s and [[photon]]s. |
|||
==== A notation simplifier : the Avogadro constant <math>N_a</math> ==== |
|||
The [[Avogadro constant]] is the number of entities in one [[mole (unit)|mole]], commonly used in [[chemistry]], where the entities are often [[atom]]s or [[molecule]]s. Its unit is inverse mole. However, the mole being a counting unit, we can consider the [[Avogadro constant]] dimensionless, and, contrary to the speed of light, the Avogadro constant doesn't convert units, but acts as a scaling factor for dealing practically with [[large number]]s. |
|||
=== Mystery and aesthetics behind constants === |
|||
[[Image:Ramanujan.jpg|thumb|left|180px|Srinivasa Ramanujan]] |
|||
[[Image:ParthenonGoldenRatio.png|thumb|right|190px|The [[Parthenon]]'s facade showing an interpretation of [[golden rectangle]]s in its proportions.]] |
|||
<div class="thumb tright"> |
|||
<div class="thumbinner" style="width:150px;"><math>e^{i\pi}+1=0\,</math> |
|||
<div class="thumbcaption">[[Euler's identity]] relating five of the most important mathematical constants.</div></div></div> |
|||
For some authors, constants, either mathematical or physical may be mysterious, beautiful or fascinating. For example, [[England|English]] [[mathematician]] [[James Whitbread Lee Glaisher|Glaisher]] (1915) writes <ref name="Site 2" />: |
|||
"No doubt the desire to obtain the values of these quantities to a great many figures is also partly due to the fact that most of them are interesting in themselves; for <math>e,\,\pi,\,\gamma,\,\log2</math>, and many other numerical quantities occupy a curious, and some of them almost a mysterious, place in mathematics, so that there is a natural tendency to do all that can be done towards their precise determination". |
|||
[[Indian]] mathematician [[Srinivasa Ramanujan]] discovered the following mysterious identity containing pi and Pythogoras' constant <math>\sqrt{2}</math>:<math>\frac{1}{\pi}=\frac{2\sqrt{2}}{9801} \sum^\infty_{k=0}\frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}</math>. |
|||
[[Steven Finch]] writes that "The fact that certain constants appear at all and then echo throughout mathematics, in seemingly independent ways, is a source of fascination."<ref>{{cite book|last=Finch|first=Steven|year=2003|title=Mathematical constants|publisher=[[Cambridge University Press]]|id=ISBN 0-521-81805-3}}</ref> |
|||
During the 1920s until his death, [[British]] [[astrophysicist]] [[Arthur Stanley Eddington|Eddington]] increasingly concentrated on what he called "[[Theory of everything|fundamental theory]]" which was intended to be a unification of [[Quantum mechanics|quantum theory]], [[theory of relativity|relativity]] and [[gravitation]]. At first he progressed along "traditional" lines, but turned increasingly to an almost [[numerology|numerological]] analysis of the dimensionless ratios of fundamental constants. In a similar fashion, [[British]] [[theoretical physicist]] [[Paul Dirac]] studied ratios of fundamental physical constant to build his [[Dirac large numbers hypothesis|large numbers hypothesis]]. |
|||
== See also == |
== See also == |
||
{{Col-begin|class=references}} |
|||
{{Col-3}} |
|||
[[Mathematical constant]]<br />[[Physical constant]]<br />[[Astronomical constant]] |
|||
{{Col-3}} |
|||
[[Scalar]]<br />[[Coefficient]]<br />[[Number]] |
|||
{{Col-3}} |
|||
[[Constant function]]<br />[[Constant of integration]]<br />[[Cosmological constant]] |
|||
{{Col-end}} |
|||
==References== |
|||
{{reflist|2}} |
|||
==Further reading== |
|||
{{Wiktionarypar|constant}} |
{{Wiktionarypar|constant}} |
||
* [[Logical constant]] |
|||
* [[Mathematical constant]] |
|||
* [[Physical constant]] |
|||
* [[Astronomical constant]] |
|||
* {{cite book |
|||
== External links == |
|||
| last = Finch |
|||
*[http://www.talkphp.com/showthread.php?t=1151 Using constants in PHP] |
|||
| first = Steven |
|||
| author = Steven Finch |
|||
| title = Mathematical Constants |
|||
| publisher = [[Cambridge University Press]] |
|||
| date = 2003 |
|||
| isbn = 0-521-81805-2}} |
|||
* {{cite web |
|||
| last = Miller |
|||
| first = Jeff |
|||
| title = Earliest Uses of Symbols for Constants |
|||
| date = 2007 |
|||
| url = http://members.aol.com/jeff570/constants.html}} |
|||
* {{cite book |
|||
| author = [[John H. Conway]] & [[Richard Guy]] |
|||
| title = The book of numbers |
|||
| publisher = Springer-Verlag New York |
|||
| date = 1996 |
|||
| isbn = 0-387-97993-X}} |
|||
==External links== |
|||
[[Category:Elementary mathematics]] |
|||
* [http://www.research.att.com/~njas/sequences/|title= On-Line Encyclopedia of Integer Sequences] |
|||
* [http://pi.lacim.uqam.ca/eng/|title= Plouffe's Inverter] |
|||
* [http://physics.nist.gov/cuu/Constants/index.html|title= Fundamental Physical Constants from NIST] |
|||
* [http://www.codata.org/|title= CODATA] |
|||
[[Category:Elementary mathematics]] |
|||
[[zh-min-nan:Tiāⁿ-sò͘]] |
[[zh-min-nan:Tiāⁿ-sò͘]] |
||
[[bg:Константа]] |
[[bg:Константа]] |
||
Revision as of 23:38, 9 December 2007
Constants are real numbers or values which are significantly interesting in some way[1]. Constants recur in both mathematics and science, therefore playing a fundamental role. They may represent universal facts -also called invariants-, link physical quantities within physical theories, check the overall consistency of physical models, simplify notation, or simply be ubiquitous. Constants are very versatile entities as they may be exact or approximate and experimentally determined, dimensionless or dimensionful with appropriate units of measurement applied, and even unspecified, when occurring for example in integrals.
When dealing with dimensionfull constants, a set of units must be chosen. Sometimes, one unit is defined in terms of another unit. For example, the metre is defined as of a light-second. This definition implies that, in metric units, the speed of light in vacuum is exactly metres per second[2]. No increase in the precision of the measurement of the speed of light could alter this numerical value expressed in metres per second.
One always talks about definable, and almost always also, computable mathematical constants - Chaitin's constant being a notable exception. However, there are still some constants -mathematical or not-, like Landau's constants[3], Erdos' reciprocal sum constants[4] or the Fermi coupling constant for which only very rough estimates are known.
As noted by Steven Finch, "All numbers are not created equal." [5] We shall therefore make the following classification: 'super-universal' constants -those appearing in different parts of science-, universal constants in a certain domain, and the more specific constants: mathematical curiosities, specific physical facts and unspecified constants.
'Super-universal' constants - occurring in different parts of science
Ubiquitous in many different fields of science, such recurring constants include , and the Feigenbaum constants which are linked to the mathematical models used to describe physical phenomena, Euclidian geometry, analysis and logistic maps respectively. However, mathematical constants such as Apéry's constant and the Golden ratio occur unexpectedly outside of mathematics.
Archimedes' constant
Pi, though having a natural definition in Euclidian geometry (the circumference of a circle of diameter 1), may be found in many different places in mathematics. Key examples include the Gaussian integral in complex analysis, nth roots of unity in number theory and Cauchy distributions in probability. However, its universality is not limited to mathematics. Indeed, various formulas in physics, such as Heisenberg's uncertainty principle, and constants such as the cosmological constant bear the constant pi. The presence of pi in physical principles, laws and formulas can have very simple explanations. For example, Coulomb's law, describing the inverse square proportionality of the magnitude of the electrostatic force between two electric charges and their distance, states that, in SI units, [6].
The exponential growth - or Napier's - constant


The exponential growth constant appears in many parts of applied mathematics. For example, as the Swiss mathematician Jacob Bernoulli discovered, e arises in compound interest. Indeed, an account that starts at $1, and yields dollars at simple interest, will yield dollars with continuous compounding. also has applications to probability theory, where it arises in a way not obviously related to exponential growth. Suppose that a gambler plays a slot machine with a one in n probability and plays it n times. Then, for large n (such as a million) the probability that the gambler will win nothing at all is (approximately) . Another application of e, also discovered in part by Jacob Bernoulli along with French mathematician Pierre Raymond de Montmort is in the problem of derangements, also known as the hat check problem[7]. Here n guests are invited to a party, and at the door each guest checks his hat with the butler who then places them into labelled boxes. But the butler does not know the name of the guests, and so must put them into boxes selected at random. The problem of de Montmort is: what is the probability that none of the hats gets put into the right box. The answer is and as the number of guests tends to infinity, approaches .
The Feigenbaum constants and
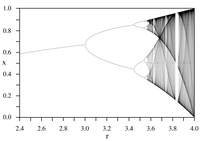
Iterations of continuous maps serve as the simplest examples of models for dynamical systems.[8] The two Feigenbaum constants appear in such iterative processes: they are mathematical invariants of logistic maps with quadratic maximum points[9] and their bifurcation diagrams.
The logistic map is a polynomial mapping, often cited as an archetypal example of how chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a seminal 1976 paper by the English biologist Robert May[10], in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. The difference equation is intended to capture the two effects or reproduction and starvation.
Apéry's constant
Despite being a special value of the Riemann zeta function, Apéry's constant arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio, computed using quantum electrodynamics[11]. Also, Pascal Wallish noted that [12], where are the neutron mass, the electron mass and the Golden ratio respectively.
The Golden ratio

The number turns up frequently in geometry, particularly in figures with pentagonal symmetry. Indeed, the length of a regular pentagon's diagonal is times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Also, it appears in the Fibonacci sequence, related to growth by recursion[13].
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavours. In these phenomena he saw the golden ratio operating as a universal law.[14] Zeising wrote in 1854:
[The Golden Ratio is a universal law] in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.[15]
Universal constants - occurring in general mathematical settings or physical phenomena
In mathematics, these constants are invariants of wide classes of objects. For example, is the invariant ratio of any circle's circumference to its diameter[16]. It is in specific mathematical settings that such natural definitions arise. For example, Catalan's constant in combinatorics, Euler-Mascheroni constant in analysis, etc. In physics, universal constants appear in the basic theoretical equations upon which the entire science rests or are the properties of the fundamental particles of physics of which all matter is constituted (the electron charge , the electron mass and the fine-structure constant ).
The Euler-Mascheroni constant
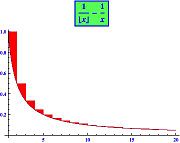
The Euler-Mascheroni constant is a recurring constant in number theory. The French mathematician De la Vallée Poussin proved in 1898 that when taking any positive integer n and dividing it by each positive integer m less than n, the average fraction by which the quotient n/m falls short of the next integer tends to as n tends to infinity. Surprisingly, this average doesn't tend to one half[17]. The Euler-Mascheroni constant also appears in Merten's third theorem and has relations to the gamma function, the zeta function and many different integrals and series. The definition of the Euler-Mascheroni constant exhibits a close link between the discrete and the continuous (see curves on the right).
Conway's constant
Conway's constant is the invariant growth rate of all derived strings similar to the look-and-say sequence (except two trivial ones)[18]. It is given by the unique positive real root of a polynomial of degree 71 with integer coefficients[19].
Khinchin's constant
If a real number is written using simple continued fraction , then, as Russian mathematician Khinchin proved in 1934, the limit as tends to infinity of the geometric mean exists, and, except for a set of measure 0, this limit is a constant, Khinchin's constant[20][21].
The speed of light and Planck's constant
The velocity of light and Planck's constant are examples of quantities that occur naturally in the mathematical formulation of certain fundamental physical theories, the former in James Clerk Maxwell's theory of electric and magnetic fields and Albert Einstein's theories of relativity, and the latter in quantum theory. For example, in special relativity, mass and energy are equivalent: [22] where is the constant of proportionality. In quantum mechanics, the energy and frequency of a photon are related by .
The speed of light is also used to express other fundamental constants [23] such as the electric constant , Coulomb's constant and the characteristic impedance of vacuum .
The electron charge and the electron mass
The electron charge and the electron mass are examples of constants that characterize the basic, or elementary, particles that constitute matter, such as the electron, alpha particle, proton, neutron, muon, and pion[24]. Many constants can be expressed using the fundamental constants . For example. it is a property of a supercurrent (superconducting electrical current) that the magnetic flux passing through any area bounded by such a current is quantized. The magnetic flux quantum is a physical constant, as it is independent of the underlying material as long as it is a superconductor. Also, the fundamental fine-structure constant where the permeability of free space is just a numerical constant equal to .
Mathematical curiosities, specific physical facts and unspecified constants
Simple representatives of sets of numbers

Some constants, such as the square root of two, Liouville's constant and Champernowne constant are not important mathematical invariants but retain interest being simple representatives of special sets of numbers, the irrational numbers[26], the transcendental numbers[27] and the normal numbers (in base 10)[28] respectively. The discovery of the irrational numbers is usually attributed to the Pythagorean Hippasus of Metapontum who proved, most likely geometrically, the irrationality of and Liouville's constant, named after French mathematician Joseph Liouville, was the first transcendental number ever constructed[29].
Chaitin's constant
In the computer science subfield of algorithmic information theory, Chaitin's constant is the real number representing the probability that a randomly-chosen Turing machine will halt, formed from a construction due to Argentine-American mathematician and computer scientist Gregory Chaitin. Amusingly, Chaitin's constant, though not being computable, it has been proven transcendental and normal.
Template:Elementbox section physicalpropTemplate:Elementbox density gpcm3nrtTemplate:Elementbox densityliq gpcm3mpTemplate:Elementbox meltingpointTemplate:Elementbox boilingpointTemplate:Elementbox heatfusion kjpmolTemplate:Elementbox heatvaporiz kjpmolTemplate:Elementbox heatcapacity jpmolkat25Template:Elementbox footerConstants representing physical properties of elements
Such constants represents characteristics of certain physical objects such as the chemical elements. Examples include density, melting point and heat of fusion. Some of the properties of gold are listed in the box on the right.
Unspecified constants
When unspecified, constants indicate classes of similar objects, commonly functions, all equal up to a constant - or, technically speaking, similarity up to a constant. Such constants appear frequently when dealing with integrals and differential equations. Though unspecified, they have a specific value, which often isn't important.

In integrals
Indefinite integrals are called indefinite because their solutions are only unique only up to a constant. For example, when working over the field of real numbers where , the constant of integration, is an arbitrary fixed real number[30]. In other words, whatever the value of , differentiating with respect to always yields .
In differential equations
In a similar fashion, constants appear in the solutions to differential equations where not enough initial values or boundary conditions are given. For example, the ordinary differential equation has solution where is an arbitrary constant.
When dealing with partial differential equations, the constants may be functions, constant with respect to some variables (but not necessarily all of them). For example, the PDE has solutions where is an arbitrary function in the variable .
Notation
Representing constants
Different symbols are used to represent and manipulate constants, such as , and . It is common, in both mathematics and physics, to express the numerical value of a constant by giving its decimal expansion. For two reasons this representation may cause problems. First, even though rational numbers all have a finite or ever-repeating decimal expansion, some numbers don't have such an expression and it would hence be impossible to completely give its value using this method. Also, the decimal expansion of a number is not necessarily unique. For example, the numbers 0.999... and 1 are equivalent[31][32], that is they represent the same constant.
Note that finding the decimal expansions of constants has often been of interest to many people. Some of the mathematical constant, such as have over (one hundred billion) known digits and very fast algorithms, as for Apéry's constant, have being constructed. In physics, it is important to know the numerical values of the fundamental constants with high accuracy for at least two reasons, the first to achieve accurate quantitative descriptions of the physical universe and the second to test the overall consistency and correctness of the basic theories of physics.
It happens that some constants differ so much from the usual kind that a special notation must be invented to represent them. Graham's number is such an example when the Knuth up-arrow notation is used[33][34].
Commonly, constants in the physical sciences are represented using the scientific notation, with, when appropriate, the inaccuracy - or measurement error - attached. When writing Planck's constant [35] it is meant that . Only the significant figures are shown and a greater precision would be superfluous, extra figures coming from experimental inaccuracies. When writing Isaac Newton's gravitational constant [36] only 6 significant figures are given.
For mathematical constants, it may be of interest to represent them using continued fractions to perform various studies, including statistical analysis. Many mathematical constants have an analytic form, that is they can constructed using well-known operations that lend themselves readily to calculation. However, Grossman's constant has no known analytic form[37].
Symbolizing and naming of constants
Symbolizing constants with letters is a frequent means of making the notation more concise. A standard convention, instigated by Euler is the 18th century, is to use lowercase letters from the beginning of the Latin alphabet or the Greek alphabet when dealing with constants in general.
Embree-Trefethen constant
Brun's constant for twin prime
Rydberg constant
cardinal number aleph naught
However, for more important constants, the symbols may be more complex and have an extra letter, an asterisk, a number, a lemniscate or use different alphabets such as Hebrew, Cyrillic or Gothic[34].
Sometimes, the symbol representing a constant is a whole word. For example, American mathematician Edward Kasner's 9-year-old nephew coined the names googol and googolplex[38][34]
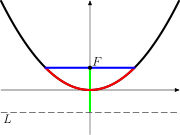
The names are either related to the meaning of the constant (parabolic constant, characteristic impedance of vacuum, twin prime constant, electric constant, conductance quantum, ...), to a specific person (Planck's constant, Sierpiński's constant, Dirac's constant, Josephson constant, ...) or both (Newtonian constant of gravitation, Bohr magneton, Fermi coupling constant[39],...).
Lumping constants
A common practice in physics is to lump constants, to simply the equations and algebraic manipulations. For example, Coulomb's constant [40] is just , and lumped together. Also, combining old constants does not necessarily make the new one less fundamental. For example, the -notably- dimensionless fine-structure constant is a fundamental constant of quantum electrodynamics and in the quantum theory of the interaction among electrons, muons and photons.
A notation simplifier : the Avogadro constant
The Avogadro constant is the number of entities in one mole, commonly used in chemistry, where the entities are often atoms or molecules. Its unit is inverse mole. However, the mole being a counting unit, we can consider the Avogadro constant dimensionless, and, contrary to the speed of light, the Avogadro constant doesn't convert units, but acts as a scaling factor for dealing practically with large numbers.
Mystery and aesthetics behind constants

For some authors, constants, either mathematical or physical may be mysterious, beautiful or fascinating. For example, English mathematician Glaisher (1915) writes [1]: "No doubt the desire to obtain the values of these quantities to a great many figures is also partly due to the fact that most of them are interesting in themselves; for , and many other numerical quantities occupy a curious, and some of them almost a mysterious, place in mathematics, so that there is a natural tendency to do all that can be done towards their precise determination".
Indian mathematician Srinivasa Ramanujan discovered the following mysterious identity containing pi and Pythogoras' constant :.
Steven Finch writes that "The fact that certain constants appear at all and then echo throughout mathematics, in seemingly independent ways, is a source of fascination."[41]
During the 1920s until his death, British astrophysicist Eddington increasingly concentrated on what he called "fundamental theory" which was intended to be a unification of quantum theory, relativity and gravitation. At first he progressed along "traditional" lines, but turned increasingly to an almost numerological analysis of the dimensionless ratios of fundamental constants. In a similar fashion, British theoretical physicist Paul Dirac studied ratios of fundamental physical constant to build his large numbers hypothesis.
See also
|
Constant function |
References
- ^ a b "Constant". Wolfram MathWorld. Retrieved 2007-12-09.
- ^ CODATA. "Speed of light in vacuum". CODATA recommended values. NIST. Retrieved 2007-08-08.
- ^ Rademacher, Hans (1943). "On the Bloch-Landau Constant". 65. American Journal of Mathematics: 387–390.
{{cite journal}}:|access-date=requires|url=(help); Cite journal requires|journal=(help) - ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. p. 163. ISBN 0-521-81805-3.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. ISBN 0-521-81805-3.
- ^ "Sphere". Wolfram MathWorld.
- ^ "Introduction to probability theory". p. 85. Retrieved 2007-12-09.
{{cite web}}: Cite uses deprecated parameter|authors=(help); Unknown parameter|licence=ignored (help) - ^ Collet & Eckmann (1980). Iterated maps on the inerval as dynamical systems. Birkhauser. ISBN 3-7643-3026-0.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. p. 67. ISBN 0-521-81805-3.
- ^ May, Robert (1976). Theoretical Ecology: Principles and Applications. Blackwell Scientific Publishers. ISBN 0-632-00768-0.
- ^ Finch, Steven. "Apéry's constant". Retrieved 2007-12-08.
- ^ "The Eagleman Prize in Mathematics and Physics".
- ^ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ^ Padovan, Richard. "Proportion: Science, Philosophy, Architecture". Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ^ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. p. preface.
- ^ "About Pi". Ask Dr. Math FAQ. Retrieved 2007-11-27.
- ^ Finch, Steven. "Euler-Mascheroni constant". Mathcad. Retrieved 2007-12-08.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. p. 453. ISBN 0-521-81805-3.
- ^ Finch, Steven. "Conway's Constant". Wolfram MathWorld. Retrieved 2007-12-07.
- ^ M. Statistical Independence in Probability, Analysis and Number Theory. Mathematical Association of America. 1959.
{{cite book}}:|first=missing|last=(help) - ^ Finch, Steven. "Khinchin's Constant". Wolfram MathWorld. Retrieved 2007-12-08.
- ^ Einstein, Albert (1905), "Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?" (PDF), Annalen der Physik, 18: 639–643, retrieved 2007-12-09 See also the english translation.
- ^ CODATA. "Values of the Fundamental Constants". CODATA recommended values. NIST. Retrieved 2007-12-09.
- ^ "Physical Constants". Encyclopaedia Britannica. Vol. 5 (15 ed.). Helen Hemingway Benton. 1974. p. 75. ISBN 0-85229-290-2.
- ^ Fowler, David (1998). "Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context" (PDF). Historia Mathematica. 25 (4): 368. Retrieved 2007-12-09.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|month=ignored (help)
Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection
High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection - ^ Bogomolny, Alexander. "Square root of 2 is irrational".
- ^ Aubrey J. Kempner (Oct 1916). "On Transcendental Numbers". Transactions of the American Mathematical Society. 17 (4): 476–482.
- ^ Champernowne, david (1933). "The onstruction of decimals normal in the scale of ten". Journal of the London Mathematical Society. 8: 254–260.
- ^ "Liouville's Constant". Wolfram MathWorld. Retrieved 2007-12-09.
- ^ Edwards, Henry. Calculus with analytic geometry (4e ed.). Prentice Hall. p. 269. ISBN 0-13-300575-5.
{{cite book}}: More than one of|author=and|last=specified (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e ed.). McGraw-Hill. p. 61. ISBN 0-07-054235-X.
{{cite book}}: Unknown parameter|theorem=ignored (help) - ^ Stewart, James (1999). Calculus: Early transcendentals (4e ed.). Brooks/Cole. p. 706. ISBN 0-534-36298-2.
- ^ Knuth, Donald (1976). "Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations". Science. 194: 1235–1242.
- ^ a b c "mathematical constants". Retrieved 2007-11-27.
- ^ CODATA. "Planck constant". CODATA recommended values. NIST. Retrieved 2007-12-09.
- ^ CODATA. "Newtonian constant of gravitation". CODATA recommended values. NIST. Retrieved 2007-12-09.
- ^ Finch, Steven. "Grossman's constant". Retrieved 2007-12-09.
- ^ Mathematics and the Imagination. Microsoft Press. 1989. p. 23.
{{cite book}}: Cite uses deprecated parameter|authors=(help) - ^ CODATA. "Fermi coupling constant". CODATA recommended values. NIST. Retrieved 2007-12-09.
- ^ "Coulomb's constant". Wolfram World of Physics. Retrieved 2007-12-09.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. ISBN 0-521-81805-3.
Further reading
- Finch, Steven (2003). Mathematical Constants. Cambridge University Press. ISBN 0-521-81805-2.
{{cite book}}: More than one of|author=and|last=specified (help) - Miller, Jeff (2007). "Earliest Uses of Symbols for Constants".
- John H. Conway & Richard Guy (1996). The book of numbers. Springer-Verlag New York. ISBN 0-387-97993-X.
External links
- On-Line Encyclopedia of Integer Sequences
- Plouffe's Inverter
- Fundamental Physical Constants from NIST
- CODATA
zh-min-nan:Tiāⁿ-sò͘ bg:Константа da:Konstant de:Konstante et:Konstant es:Constante eo:Konstanto fr:Constante gd:Cunbhal ko:상수 id:Konstanta it:Costante lt:Konstanta nl:Constant (eigenschap) ja:定数 no:Konstant pt:Constante ru:Константа simple:Constant sr:Константа fi:Vakio sv:Konstant th:ค่าคงตัว uk:Константа zh:常数














































































