Jump to content

Ptolemy

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Stoa (talk | contribs) at 15:58, 2 November 2007 (Revert to revision 168490488 dated 2007-11-01 11:54:25 by AdnanSa using popups). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Template:Two other uses

Ptolemy
A medieval artist's rendition of Claudius Ptolemaeus.
Bornafter 83 AD
Roman Province of Egypt
Died161 AD
Roman Province of Egypt
Occupation(s)mathematician, geographer, astronomer, astrologer

Claudius Ptolemaeus (Greek: Κλαύδιος Πτολεμαῖος; after 83 – 161 AD), known in English as Ptolemy, was a Greek[1] or Egyptian[2] mathematician, geographer, astronomer, and astrologer who flourished in Alexandria, Roman Egypt.

Ptolemy was the author of several scientific treatises, three of which would be of continuing importance to later Islamic and European science. The first is the astronomical treatise that is now known as the Almagest (in Greek, Η Μεγάλη Σύνταξις, "The Great Treatise", originally Μαθηματικἠ Σύνταξις, "Mathematical Treatise"). The second is the Geography, which is a thorough discussion of the geographic knowledge of the Greco-Roman world. The third is the astrological treatise known as the Tetrabiblos ("Four books") in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day.

Name

Though considered a member of Alexandria's Greek society, Ptolemy's biographical details were never recorded. Some scholars have assumed that Ptolemy may have been a Greek[1][3] while others have assumed that he may have been a Hellenized Egyptian.[2][3][4][5][6] He was often known in later Arabic sources as "the Upper Egyptian",[7] suggesting that he may have had origins in southern Egypt.[5] Ptolemy is also known to have used Babylonian astronomical data.[8][9]

Ptolemy is a Greek name. It occurs once in Greek mythology, and is of Homeric form. It was quite common among the Macedonian upper class at the time of Alexander the Great, and there are several among Alexander's army, one of whom made himself King of Egypt: Ptolemy I Soter; all the Kings after him, until Rome conquered Egypt, were also Ptolemies. There is no evidence on Ptolemy's ancestry, but most scholars consider it unlikely that Ptolemy was related to the royal family.[citation needed]

Claudius is a Roman name; it implies Ptolemy was a Roman citizen. It would have been customary for the first Ptolemy to be a citizen, whether Ptolemy or an ancestor, to take the nomen from a Roman called Claudius, who was in some sense responsible for the citizenship. If, as was not uncommon, this Roman was the Emperor, the citizenship would have been granted between 14 and 68 AD, when the Claudii were Emperors. The astronomer would also have had a praenomen, which remains unknown. The Persian mathematician, astronomer, and geographer Muhammad ibn Mūsā al-Khwārizmī (ca. 780-850 AD), the founder of algebra, who revised and updated Ptolemy's Geography, was of the opinion that Ptolemy was a descendant of a Roman emperor named Claudius and that was why he and his ancestors possessed that name.

Astronomy

Further information: Almagest

The Almagest is the only surviving comprehensive ancient treatise on astronomy. Babylonian astronomers had developed arithmetical techniques for calculating astronomical phenomena; Greek astronomers such as Hipparchus had produced geometric models for calculating celestial motions; Ptolemy, however, claimed to have derived his geometrical models from selected astronomical observations by his predecessors spanning more than 800 years, though astronomers have for centuries suspected that his models' parameters were adopted independently of observations. Ptolemy presented his astronomical models in convenient tables, which could be used to compute the future or past position of the planets.[10] The Almagest also contains a star catalogue, which is an appropriated version of a catalogue created by Hipparchus. Its list of forty-eight constellations is ancestral to the modern system of constellations, but unlike the modern system they did not cover the whole sky (only the sky Hipparchus could see). Through the Middle Ages it was spoken of as the authoritative text on astronomy, with its author becoming an almost mythical figure, called Ptolemy, King of Alexandria.[11] The Almagest was preserved, like most of Classical Greek science, in Arabic manuscripts (hence its familiar name). Because of its reputation, it was widely sought and was translated twice into Latin in the 12th century, once in Sicily and again in Spain.[12] Ptolemy's model, like those of his predecessors, was geocentric and was almost universally accepted until an equally systematic presentation of a heliocentric geometrical model by Nicolaus Copernicus.

His Planetary Hypotheses went beyond the mathematical model of the Almagest to present a physical realization of the universe as a set of nested spheres,[13] in which he used the epicycles of his planetary model to compute the dimensions of the universe. He estimated the Sun was at an average distance of 1210 Earth radii while the radius of the sphere of the fixed stars was 20,000 times the radius of the Earth.[14]

Ptolemy presented a useful tool for astronomical calculations in his Handy Tables, which tabulated all the data needed to compute the positions of the Sun, Moon and planets, the rising and setting of the stars, and eclipses of the Sun and Moon. Ptolemy's Handy Tables provided the model for later astronomical tables or zījes. In the Phaseis (Risings of the Fixed Stars) Ptolemy gave a parapegma, a star calendar or almanac based on the appearances and disappearances of stars over the course of the solar year.

His model and computational methods were adopted and modified in the Arabic speaking world and in India, since they were of sufficient accuracy to satisfy the needs of astronomers, astrologers, timekeepers, calendar keepers, and navigators.

Geographia

Main article: Geographia (Ptolemy)

Ptolemy's other main work is his Geographia. This too is a compilation of what was known about the world's geography in the Roman Empire during his time. He relied somewhat on the work of an earlier geographer, Marinos of Tyre, and on gazetteers of the Roman and ancient Persian Empire, but most of his sources beyond the perimeter of the Empire were unreliable.

The first part of the Geographia is a discussion of the data and of the methods he used. As with the model of the solar system in the Almagest, Ptolemy put all this information into a grand scheme. Following Marinos, he assigned coordinates to all the places and geographic features he knew, in a grid that spanned the globe. Latitude was measured from the equator, as it is today, but Ptolemy preferred in book 8 to express it as the length of the longest day rather than degrees of arc (the length of the midsummer day increases from 12h to 24h as you go from the equator to the polar circle). In books 2 through 7, he used degrees and put the meridian of 0 longitude at the most western land he knew, the "Blessed Islands", probably the Cape Verde islands (not the Canary Islands, as long accepted) as suggested by the location of the six dots labelled the "FORTUNATA" islands near the left extreme of the blue sea of Ptolemy's map here reproduced.

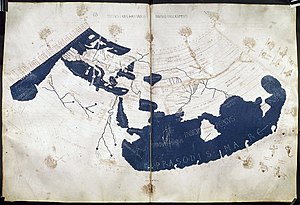
A 15th century manuscript copy of the Ptolemy world map, reconstituted from Ptolemy's Geographia (circa 150), indicating the countries of "Serica" and "Sinae" (China) at the extreme right, beyond the island of "Taprobane" (Sri Lanka, oversized) and the "Aurea Chersonesus" (Malay Peninsula).

Ptolemy also devised and provided instructions on how to create maps both of the whole inhabited world (oikoumenè) and of the Roman provinces. In the second part of the Geographia he provided the necessary topographic lists, and captions for the maps. His oikoumenè spanned 180 degrees of longitude from the Blessed Islands in the Atlantic Ocean to the middle of China, and about 80 degrees of latitude from Thule Shetlands to anti-Meroe (east coast of Africa); Ptolemy was well aware that he knew about only a quarter of the globe, and an erroneous extension of China southward blocked off any awareness of the Pacific Ocean.

The maps in surviving manuscripts of Ptolemy's Geographia, however, date only from about 1300, after the text was rediscovered by Maximus Planudes. It seems likely that the topographical tables in books 2-7 are cumulative texts - texts which were altered and added to as new knowledge became available in the centuries after Ptolemy (Bagrow 1945). This means that information contained in different parts of the Geography is likely to be of different date.

A printed Ptolemaic map from the 16th century

Maps based on scientific principles had been made since the time of Eratosthenes (3rd century BC), but Ptolemy improved projections. It is known that a world map based on the Geographia was on display in Autun, France in late Roman times. In the 15th century Ptolemy's Geographia began to be printed with engraved maps; the earliest printed edition with engraved maps was produced in Bologna in 1477, followed quickly by a Roman edition in 1478 (Campbell, 1987). An edition printed at Ulm in 1482, including woodcut maps, was the first one printed north of the Alps. The maps look distorted as compared to modern maps, because Ptolemy's data were inaccurate. One reason is that Ptolemy estimated the size of the Earth as too small: while Eratosthenes found 700 stadia for a great circle degree on the globe, in the Geographia Ptolemy uses 500 stadia. It is highly probable that these were the same stadion since Ptolemy switched from the former scale to the latter, between the Syntaxis and the Geographia and severely readjusted longitude degrees accordingly. If they both used the Attic stadion of about 185 meters, then the older estimate is 1/6 too large, and Ptolemy's value is 1/6 too small, a difference recently explained as due to ancient scientists' use of simple methods of measuring the earth, which were corrupted either high or low by a factor of 5/6, due to air's bending of horizontal light rays by 1/6 of the earth's curvature. See also Ancient Greek units of measurement and History of geodesy.

Because Ptolemy derived many of his key latitudes from crude longest day values, his latitudes are erroneous on average by roughly a degree (2 degrees for Byzantium, 4 degrees for Carthage), though capable ancient astronomers knew their latitudes to more like a minute. (Ptolemy's own latitude was in error by 14'.) He agreed (Geographia 1.4) that longitude was best determined by simultaneous observation of lunar eclipses, yet he was so out of touch with the scientists of his day that he knew of no such data more recent than 500 years ago (Arbela eclipse). When switching from 700 stadia per degree to 500, he (or Marinos) expanded longitude differences between cities accordingly (a point 1st realized by P.Gosselin in 1790), resulting in serious over-stretching of the earth's east-west scale in degrees, though not distance. Achieving highly precise longitude remained a problem in geography until the invention of the marine chronometer at the end of the 18th century. It must be added that his original topographic list cannot be reconstructed: the long tables with numbers were transmitted to posterity through copies containing many scribal errors, and people have always been adding or improving the topographic data: this is a testimony to the persistent popularity of this influential work in the history of cartography.

Interestingly, some of his maps shown parts of the "new world". This topography fits apparently parts of New England and Canada. Some have seen Antarctica and South America too, misplaced near China. All this always before Columbus travel. This is similar to Piri Reis enigmas. [2]

Astrology

The mathematician Claudius Ptolemy 'the Alexandrian' as imagined by a 16th century artist

Ptolemy's treatise on astrology, the Tetrabiblos, was the most popular astrological work of antiquity and also enjoyed great influence in the Islamic world and the medieval Latin West. The Tetrabiblos is an extensive and continually reprinted treatise on the ancient principles of horoscopic astrology in four books (Greek tetra means "four", biblos is "book"). That it did not quite attain the unrivalled status of the Almagest was perhaps because it did not cover some popular areas of the subject, particularly electional astrology (interpreting astrological charts for a particular moment to determine the outcome of a course of action to be initiated at that time), and medical astrology.

The great popularity that the Tetrabiblos did possess might be attributed to its nature as an exposition of the art of astrology and as a compendium of astrological lore, rather than as a manual. It speaks in general terms, avoiding illustrations and details of practice. Ptolemy was concerned to defend astrology by defining its limits, compiling astronomical data that he believed was reliable and dismissing practices (such as considering the numerological significance of names) that he believed to be without sound basis.

Much of the content of the Tetrabiblos may well have been collected from earlier sources; Ptolemy's achievement was to order his material in a systematic way, showing how the subject could, in his view, be rationalized. It is, indeed, presented as the second part of the study of astronomy of which the Almagest was the first, concerned with the influences of the celestial bodies in the sublunar sphere. Thus explanations of a sort are provided for the astrological effects of the planets, based upon their combined effects of heating, cooling, moistening, and drying.

Ptolemy's astrological outlook was quite practical: he thought that astrology was like medicine, that is conjectural, because of the many variable factors to be taken into account: the race, country, and upbringing of a person affects an individual's personality as much if not more than the positions of the Sun, Moon, and planets at the precise moment of their birth, so Ptolemy saw astrology as something to be used in life but in no way relied on entirely.

Music

Ptolemy also wrote an influential work, Harmonics, on music theory and the mathematics of music. After criticizing the approaches of his predecessors, Ptolemy argued for basing musical intervals on mathematical ratios (in contrast to the followers of Aristoxenus and in agreement with the followers of Pythagoras) backed up by empirical observation (in contrast to the overly theoretical approach of the Pythagoreans). Ptolemy wrote about how musical notes could be translated into mathematical equations and vice versa in Harmonics. This is called Pythagorean tuning because it was first discovered by Pythagoras. However, Pythagoras believed that the mathematics of music should be based on the specific ratio of 3:2 whereas Ptolemy merely believed that it should just generally involve tetrachords and octaves. He presented his own divisions of the tetrachord and the octave, which he derived with the help of a monochord. Ptolemy's astronomical interests also appeared in a discussion of the music of the spheres.

Other works

His Optics, a work which survives only in a poor Arabic translation and in about twenty manuscripts of a Latin translation of the Arabic, made by Eugene of Palermo (circa 1154). In it he writes about properties of light, including reflection, refraction and colour. The work is a significant part of the early history of optics.

Named after Ptolemy

Footnotes

  1. ^ a b enc. Britannica 2007, "Claudius Ptolemaeus" [1]
  2. ^ a b George Sarton (1936). "The Unity and Diversity of the Mediterranean World", Osiris 2, p. 406-463 [429].
  3. ^ a b Victor J. Katz (1998). A History of Mathematics: An Introduction, p. 184. Addison Wesley, ISBN 0321016181.

    "But what we really want to know is to what extent the Alexandrian mathematicians of the period from the first to the fifth centuries C.E. were Greek. Certainly, all of them wrote in Greek and were part of the Greek intellectual community of Alexandria. And most modern studies conclude that the Greek community coexisted [...] So should we assume that Ptolemy and Diophantus, Pappus and Hypatia were ethnically Greek, that their ancestors had come from Greece at some point in the past but had remained effectively isolated from the Egyptians? It is, of course, impossible to answer this question definatively. But research in papyri dating from the early centuries of the common era demonstrates that a significant amount of intermarriage took place between the Greek and Egyptian communities [...] And it is known that Greek marriage contracts increasingly came to resemble Egyptian ones. In addition, even from the founding of Alexandria, small numbers of Egyptians were admitted to the privaleged classes in the city to fulfill numerous civic roles. Of course, it was essential in such cases for the Egyptians to become "Hellenized," to adopt Greek habits and the Greek language. Given that the Alexandrian mathematicians mentioned here were active several hundred years after the founding of the city, it would seem at least equally possible that they were ethnically Egyptian as that they remained ethnically Greek. In any case, it is unreasonable to portray them with purely European features when no physical descriptions exist."
  4. ^ John Horace Parry (1981). The Age of Reconnaissance, p. 10. University of California Press. ISBN 0520042352.
  5. ^ a b Martin Bernal (1992). "Animadversions on the Origins of Western Science", Isis 83 (4), p. 596-607 [602, 606].
  6. ^ Ptolemy, Columbia Encyclopedia, Sixth Edition, 2007.
  7. ^ J. F. Weidler (1741). Historia astronomiae, p. 177. Wittenberg: Gottlieb. (cf. Martin Bernal (1992). "Animadversions on the Origins of Western Science", Isis 83 (4), p. 596-607 [606].)
  8. ^ Asger Aaboe, Episodes from the Early History of Astronomy, New York: Springer, 2001), p. 62-65.
  9. ^ Alexander Jones, "The Adaptation of Babylonian Methods in Greek Numerical Astronomy," in The Scientific Enterprise in Antiquity and the Middle Ages, p. 99.
  10. ^ Bernard R. Goldstein, "Saving the Phenomena: The Background to Ptolemy's Planetary Theory", Journal for the History of Astronomy, 28 (1997): 1-12
  11. ^ S. C. McCluskey, Astronomies and Cultures in Early Medieval Europe, Cambridge: Cambridge Univ. Pr. 1998, pp. 20-21.
  12. ^ Charles Homer Haskins, Studies in the History of Mediaeval Science, New York: Frederick Ungar Publishing, 1967, reprint of the Cambridge, Mass., 1927 edition
  13. ^ Dennis Duke, Ptolemy's Cosmology
  14. ^ Bernard R. Goldstein, ed., The Arabic Version of Ptolemy's Planetary Hypotheses, Transactions of the American Philosophical Society, 57, 4 (1967), pp. 9-12.

See also

References

Texts and translations

  • Berggren, J. Lennart and Jones, Alexander. 2000. Ptolemy's Geography: An Annotated Translation of the Theoretical Chapters. Princeton and Oxford: Princeton University Press. ISBN 0-691-01042-0.
  • Nobbe, C. F. A., ed. 1843. Claudii Ptolemaei Geographia. 3 vols. Leipzig: Carolus Tauchnitus. (The most recent edition of the complete Greek text)
  • Stevenson, Edward Luther. Trans. and ed. 1932. Claudius Ptolemy: The Geography. New York Public Library. Reprint: Dover, 1991. (This is the only complete English translation of Ptolemy's most famous work. Unfortunately, it is marred by numerous mistakes and the placenames are given in Latinised forms, rather than in the original Greek).
  • Stückelberger, Alfred and Graßhoff, Gerd, eds. 2006. Ptolemaios, Handbuch der Geographie, Griechisch-Deutsch. 2 vols. Basel. Schwabe Verlag. ISBN-13 978-3-7965-2148-5. (Massive 1018 pp. scholarly edition by a team of a dozen scholars that takes account of all known manuscripts, with facing Greek and German text, footnotes on manuscript variations, color maps, and a CD with the geographical data)

Other references

  • Bagrow, L. 1945. "The Origin of Ptolemy's Geographia". Geografiska Annaler 27:318-387.
  • Campbell, T. 1987. The Earliest Printed Maps. British Museum Press.
  • Neugebauer, Otto 1975 A History of Ancient Mathematical Astronomy. 3 vols, Berlin and New York: Sprnger Verlag.
  • Taub, Liba Chia 1993 Ptolemy's Universe: The Natural Philosophical and Ethical Foundations of Ptolemy's Astronomy. Chicago: Open Court Press. ISBN 0-8126-9229-2
Wikiquote has quotations related to Ptolemy.
Wikimedia Commons has media related to Ptolemy.

Primary sources

Secondary material

Template:Persondata

Retrieved from "https://en.wikipedia.org/w/index.php?title=Ptolemy&oldid=168748816"