Wikipedia:Reference desk/Mathematics

Welcome to the mathematics section
of the Wikipedia reference desk.

skip to bottom

Select a section:

• Computing
• Entertainment
• Humanities
• Language
• Mathematics
• Science
• Miscellaneous
• Archives

Want a faster answer?

Main page: Help searching Wikipedia

   

How can I get my question answered?

• Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
• Post your question to only one section, providing a short header that gives the topic of your question.
• Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
• Don't post personal contact information – it will be removed. Any answers will be provided here.
• Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
• Note:
  • We don't answer (and may remove) questions that require medical diagnosis or legal advice.
  • We don't answer requests for opinions, predictions or debate.
  • We don't do your homework for you, though we'll help you past the stuck point.
  • We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

• The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

See also:

• Teahouse
• Help desk
• Village pump
• Help manual

February 16

Round 0.45 or 0.49 or 0.50

For 5.55555 would be closer to 6? for 9.45 rounds to 9.5 bt I dunno if 45 cound round the 9 to a 10 or it pulls it back down to 9. In 8th grade math somebody told me .49 or lower I round back down .51 or above I round the number up. Would .50 bring the whole number up or keep it down? --69.229.36.56 (talk) 00:19, 16 February 2010 (UTC)

What? --COVIZAPIBETEFOKY (talk) 01:27, 16 February 2010 (UTC)

This is the famous "primary school mathematics". Most primary school "mathematics textbooks" dictate that 9.45 rounds to 9, and that 5.55555 rounds to 6. The number 9.5 will round to 10 because, for some weird reason, "primary school mathematics" thinks that 9.5 is closer to 10 than it is to 9. So .50 brings the number up but technically speaking, that convention makes little sense. When "rounding numbers" be sure to note that a decimal is rounded to the whole number nearest to it; therefore, .49 or lower is "rounded down" because .49 is closer to 0 than it is to 1, and .51 or above is "rounded up" because .51 is closer to 1 than it is to 0. And your "primary school mathematics teachers" will probably tell you that .50 is rounded up, but they are sure to be clueless if you ask them why (I am clueless as well but I am not the one who created or practiced that convention...). PST 02:18, 16 February 2010 (UTC)

I like to think of it this way: If you're piloting a plane, and you get half way with half a tank of fuel left, are you going to go back to fill up or carry on to your destination? This has no bearing on mathematics, but perhaps the assumptions that underlie the convention (see half-full glass) are related. Or, I might be spouting nonsense. —Anonymous Dissident^Talk 11:59, 16 February 2010 (UTC)

See Rounding. And always rounding up has no great merits compared to rounding down. Rounding to even will give better overall behaviour, there is an interesting story there about a stock exchange always rounding down. Dmcq (talk) 02:29, 16 February 2010 (UTC)

@PST: the obvious answer is that in the absence of any pressing arguments for either direction, rounding .50 up is preferable because it makes a simpler rule ("round it down if the next digit is 0 to 4, and round it up if it is 5 to 9").—Emil J. 11:46, 16 February 2010 (UTC)

I think the poster was thinking that perhaps rounding twice in succession with an intermediate precision should lead to the same result as rounding once to the final precision. There's no reason for that to hold and 'double rounding' is an implementation problem with java on ix86 pc's because of them sometimes holding floating point in registers to higher precision than they store them. Dmcq (talk) 12:00, 16 February 2010 (UTC)

I always used to explain that the rule (for science) is to round up from half-way because the percentage error will then always be smaller, but that, in statistics, a different rule such as "round to even" would help to avoid bias. Dbfirs 22:52, 16 February 2010 (UTC)

By the same idea one can sometimes defend rounding with the division at the geometric mean of the two possibilities so when rounding to either 9 or 10 the mid point is 9.486 Dmcq (talk) 23:08, 16 February 2010 (UTC)

Cauchy Sequence Ring and Null Sequences - Square root of 2

Hi all,

I've been playing around with the Ring of Cauchy Sequences in the rational numbers C and the subset of Null sequences N (tends to 0 as n tends to infinity). I've shown that N is a maximal ideal in C, which means C/N is a field - 2 members in this field are equal if they differ by a null sequence I believe, a.k.a. they share the same limit as n tends to infinity - so we can find a subfield of all the sequences which have a rational limit and identify that with the rationals themselves: however, I'm told that the solution x²=2 has a solution in this field, and I have no idea why. (Assuming I've got the right subfield - the problem i'm doing says deduce C/N is a field with a subfield which can be identified with Q - that must be the limits of the sequences, right?) - So would anyone be able to explain to me why the solution x^2=2 exists in this field, yet of course doesn't in the rationals themselves?

Many thanks, 82.6.96.22 (talk) 08:21, 16 February 2010 (UTC)

Let $x\in \mathbb {R}$ be arbitrary, and let ${(x_{n})}_{n\in \mathbb {N} }$ be a sequence of rational numbers converging to x (any such sequence is necessarily Cauchy). The coset of N (the ideal of null sequences) by ${(x_{n})}_{n\in \mathbb {N} }$ "behaves like" the real number x relative to the other elements in $C\setminus N$. Therefore, we would expect that the field $C\setminus N$ is in fact isomorphic to the field of real numbers (which contains the field of rational numbers as a subfield). Therefore, you are indeed correct that the field of cosets of N by elements in C that have rational limits is isomorphic to $\mathbb {Q}$.

If you would like a more formal proof of $C\setminus N\cong \mathbb {R}$, consider the function $f:\mathbb {R} \to C\setminus N$ defined by $f(r)=s_{r}+N$, where $s_{r}$ is a sequence consisting only of rational terms that converges to (the real number) r. If we consider an arbitrary Cauchy sequence c in C, it must have a real number limit x, whence $s_{x}-c\in N$ (the limit of this difference is zero by standard limit laws); hence the element $c+N\in C\setminus N$ is the image of x under f, and the map f is surjective. By a similar "coset type argument" one can see that the map f is also injective (for completeness, note that $s_{x}-s_{y}$ converges to $x-y$ (and is therefore in N if and only if $x=y$). It should now be clear that f is an isomorphism (being a bijective homomorphism).

Now that $C\setminus N\cong \mathbb {R}$ has been established, it is easy to see that a solution to the equation $x^{2}-2=0$ exists in $C\setminus N$; in fact, it can be shown that "many more" polynomial equations have solutions in this field, as there is nothing special about the given equation in the previous argument. Hope this helps (and feel free to ask any furthur questions if necessary). PST 09:35, 16 February 2010 (UTC)

Oh I see - I tried to phrase the question as the original problem was worded, but it wasn't specific which field it was referring to which had a solution to x^2=2: I assumed they were talking about the subfield isomorphic to Q having a solution to x^2=2; do you think they meant the whole field C/N which is isomorphic to R having a solution? I just assumed it was the subfield because x^2=2 having a solution isn't really remarkable in R, but have I misunderstood things? Thanks very much - 82.6.96.22 (talk) 20:00, 16 February 2010 (UTC)

(I spent the day thinking about it and couldn't work out a way to correspond any rational-limited sequence to x^2=2, so it'd make me feel a lot better to know I'd been trying to answer the wrong question! Although then, it seems more appropriate to ask why would we expect it not to have a solution in the first place?) 82.6.96.22 (talk) 20:08, 16 February 2010 (UTC)

Well, if a field F is isomorphic to $\mathbb {Q}$, it should have "the same algebraic structure as $\mathbb {Q}$". Therefore, if $x\in F$ has the property that $x^{2}=1+1=2$, the image of x under an isomorphism from F to $\mathbb {Q}$ (let us denote an arbitrary such isomorphism by "f") also has the same property (since $[f(x)]^{2}=f(x^{2})=f(2)=f(1)+f(1)=1+1=2$). In particular, the problem would not be correct if it required one to prove that a field isomorphic to $\mathbb {Q}$ contains a solution to the equation $x^{2}-2=0$. Does this answer your questions?

My first thought when you posed the problem was that it had little to do with analytic concepts (such as Cauchy sequences and limits) but more to do with algebra (algebra "disguised" within analysis, if you like). Thus I approached the problem by looking at it algebraically rather than analytically. PST 08:09, 17 February 2010 (UTC)

Yes, I admit when I asked it, I was surprised that there could be something like an isomorphism preserving structure but somehow failing to retain such a fundamental property as the irrationality of square roots in Q - the question makes much more sense that way, thankyou ever so much for the help :) 82.6.96.22 (talk) 08:26, 17 February 2010 (UTC)

If I understand the notation correctly, f does not work; for C is the ring of Cauchy sequences over the rationals, so (for example) $f(\pi )=(\pi ,\pi ,\ldots ,)+N$ is not a member of $C/N$. As for actually finding an isomorphism between $C/N$ and $\mathbb {R}$, this would depend on how $\mathbb {R}$ is defined (seeing as I would define it as being equal to C / N that makes the problem very easy for me...). Eric. 131.215.159.171 (talk) 23:58, 17 February 2010 (UTC)

You are right; apologies to the OP for that silly mistake on my part. The assertion, namely that $C/N\cong \mathbb {R}$, remains correct; we merely need replace $f(x)=(x,x,x,\cdots )$ by a sequence with rational terms converging to x (such a sequence exists by the density of the space of rational numbers in the space of real numbers). The mistake is now corrected above. Thanks Eric, PST 00:43, 18 February 2010 (UTC)

Solving sin(x^2)

A few days ago a student who I was tutoring had to find all solutions to $\sin(3t)={\frac {\sqrt {3}}{2}}$. That was no problem, but it had occured to me that the only way I knew to solve something like $\sin(x^{2})={\frac {1}{2}}$ was by treating it as a composition of functions. So I'm curious is there another relatively elementary way to solve this? A math-wiki (talk) 08:37, 16 February 2010 (UTC)

Could you please clarify what exactly you mean? If we determine the set of all z such that the sine of z is ${\frac {1}{2}}$, the set of all square roots of elements in this set would be the solution set of $\sin(x^{2})={\frac {1}{2}}$ (which is, I think, what you meant by "solving the equation by treating it as a composition of functions"). Other than this method, I do not think that there exists an elementary method to solve these sorts of equations (and even if such an elementary method existed for $\sin(x^{2})={\frac {1}{2}}$, it is unlikely it would generalize to $\sin(g(x))={\frac {1}{2}}$ for an arbitrary function g whose inverse exists and is explicitly known). PST 09:45, 16 February 2010 (UTC)

I think I partially answered my own question, wouldn't taking the arcsin (as a multivalued function?, i.e. taking ALL solutions not just the ones the proper inverse function would give) then taking the square root of both sides accounting for +/- solutions to the root on the side without the variable work? That is;

$\arcsin(\sin(x^{2}))=\arcsin({\frac {1}{2}})$ (arcsin here is NOT the usual inverse function but rather a different operator all together that give the whole solution set for sin(x)=1/2)

$x^{2}={\frac {\pi }{6}}+2n\pi ,{\frac {5\pi }{6}}+2n\pi$

$x=\pm {\sqrt {{\frac {\pi }{6}}+2n\pi }},\pm {\sqrt {{\frac {5\pi }{6}}+2n\pi }}$

The one problem i have with this is its essentially solving it in the follow manner, just written differently.

Let $f(x)=\sin {x}$ and $g(x)=x^{2}$, solve $f(x)={\frac {1}{2}}$ for x.

Then for all solutions C of $f(x)={\frac {1}{2}}$, solve $x^{2}=C$.

This is what I meant by solving it as a composition of function (e.g. $f(g(x))={\frac {1}{2}}$ was our original problem and all the solutions to $x^{2}=C$ are precisely the solutions to $f(g(x))={\frac {1}{2}}$) A math-wiki (talk) 09:12, 17 February 2010 (UTC)

Sum of reciprocals of cubics

I need to find the sum of the series ${\frac {1}{2\times 5\times 8}}+{\frac {1}{5\times 8\times 11}}+{\frac {1}{8\times 11\times 14}}+...$

It's pretty obvious that the nth term is ${\frac {1}{(3n-1)(3n+2)(3n+5)}}$ but I'm not sure if that helps me find the sum to n terms, and the sum to infinity.--220.253.101.175 (talk) 08:43, 16 February 2010 (UTC)

I think you can write out that general term as a partial fraction decomposition giving you a sum like A/(3n-1) + B/(3n+2) + C/(3n+5) (you have to solve for the coefficients) and then you can handle those series one at a time. (Hmm, wait, that's probably no good, they would all diverge). There are powerful ways of doing these sums with contour integrals but that's probably not what you want, and I don't remember anything about how to do it any more. 66.127.55.192 (talk) 10:34, 16 February 2010 (UTC)

No continue on with that fractional decomposition idea and write down the first few terms decomposed that way. You should spot something about the terms which makes things easy. Dmcq (talk) 11:44, 16 February 2010 (UTC)

More details. This case is particularly simple because the coefficients A B C above give you a telescoping series (write the partial sum for n from 1 to m as a linear combination of the three partial sums, respectively with coefficients A B C; observe that they are in fact the same partial sum, up to a shift and up to the first and the last terms, and note that A+B+C=0). So this is just a three-term version of the easier telescopic sum of 1/n(n+1) shown in the link, and you can even write an analog closed formula for the sum for n from 1 to m. The analog, more general situation, where you don't have cancellations, may be treated using the logarithmic asymptotics for the finite sums $\scriptstyle \sum _{n=1}^{N}1/(an+b)$, that produces an exact value for the sum of the series. (1/60) --pma 15:26, 16 February 2010 (UTC)

What's the name for a holomorphic function (e.g. a logarithmic function) not included in any other holomorphic function?

HOOTmag (talk) 09:31, 16 February 2010 (UTC)

What do you mean by "included"? Staecker (talk) 15:27, 16 February 2010 (UTC)

If "included" refers to inclusion of graphs, that is extension, I'd say "maximally defined" or "maximally extended" or "defined on a maximal domain of analyticity of its". Check also domain of holomorphy for related concepts. --pma 15:43, 16 February 2010 (UTC)

I mean a holomorphic function which can't be more extended analytically. Is the term "maximally" a common usage for holomorphic functions which can't be more extended analytically? And why shouldn't we call them simply: "maximal holomorphic functions"? HOOTmag (talk) 16:28, 16 February 2010 (UTC)

As far as I see, the adjective "maximal" with "function" or so, usually refers to other partial orders than extension, and I suspect that "maximal holomorphic function" may leave some doubts on its meaning (although personally I would vote for it). By the way, "maximal solution" in the context of ODEs also sounds ambiguous (some use it the sense of extension, some in the sense of pointwise order). "Maximal holomorphic extension" (of a function/germ) or "maximally extended holomorphic function" is longer but doesn't seem to need explanation, and in fact reflects a standard general usage (e.g. "maximally extended" gets more than 20,000 google results). So, if you need a short form to be used several times e.g. in a paper I'd suggest to give the explicit definition first. Of course, the best should be finding an expression from an authoritative source. --pma 17:55, 16 February 2010 (UTC)

In Google, the expression "maximally extended" appears in various contexts, including physics (like in "maximally extended universes"), geometry (like in "maximally extended polygons"), and the like. However, if you say that this expression "reflects a standard general usage" (in our context of holomorphic functions) then I accept your testimony.

How about: "maximally extended analytically"? Is it a common expression as well? Anyways, it's less ambiguous, isn't it? HOOTmag (talk) 18:31, 16 February 2010 (UTC)

Yes.. Also in google "maximal holomorphic extension" gives a hundred of results, among which some books and papers that may give you some hint, e.g. [1]--pma 21:59, 16 February 2010 (UTC)

THANKXS. HOOTmag (talk) 01:42, 17 February 2010 (UTC)

Sobbmub (talk) 15:47, 16 February 2010 (UTC)How can we solve it?Method please

18*4/6+77-5

Get a calculator. Turn it on. Type 18. Press x. Type 4. Press ÷. Type 6. Press +. Type 77. Press -. Type 5. Press =. I believe the calculator will display 84. -- kainaw™ 15:49, 16 February 2010 (UTC)

Not if it is a reverse Polish notation calculator! Nimur (talk) 15:54, 16 February 2010 (UTC)

Depending on the reason the question was asked, order of operations might help. - Jarry1250 ^{[Humorous? Discuss.]} 15:58, 16 February 2010 (UTC)

Sobbmub, please do not re-post the same question multiple times. You've already received answers here. Nimur (talk) 16:06, 16 February 2010 (UTC)

If you search using google just stick the expression in as your search. The nice people at google will quickly work it out on their calculators and send the result back to you. Much easier and faster than asking the wikipedia reference desk. Dmcq (talk) 17:06, 16 February 2010 (UTC)

Aren't they supposed to be imps?—Emil J. 17:18, 16 February 2010 (UTC)

Cancel the 18 and the 6 to get 3, BEFORE multiplying. It's not strictly necessary to do it that way, but in some contexts it's useful, so I make a habit of it. Michael Hardy (talk) 22:05, 16 February 2010 (UTC)

math conversion

is there a website where I can learn how to convert a fraction into a percentage, convert percentage into a fraction, convert percentage into a decimal, convert decimal into percentage, convert decimal into fraction and convert into fraction into decimal? —Preceding unsigned comment added by 74.14.118.34 (talk) 16:20, 16 February 2010 (UTC)

Try one of these, perhaps: [2] [3] [4]. Or just search for it. —Bkell (talk) 16:56, 16 February 2010 (UTC)

• convert fraction into decimal - Divide numerator by denominator. ex: 3/4 = 3 divided by 4 --> .75
• convert decimal into percentage - Multiply the number by 100. ex: .75 * 100 = 75%
• convert fraction into a percentage - Convert fraction to decimal, then decmial to percentage. ex: 3/4 = .75. .75 * 100 = 75%
• convert decimal into fraction - in the simplest terms, just put the decimal as the numerator. ex: .341 = .341/1. This can then (sometimes) be simplified. ex: .5 = .5/1. .5/1 * (2/2) = 1/2, but sometimes the decimal over 1 is the best you can do.
• convert percentage into a fraction - Divide percentage by 100 ex: 75% = 75/100
• convert percentage into a decimal - convert percentage to fraction, then convert fraction to decimal. ex: 75% = 75/100 = .75

Though I'm sure some of those sites describe it better. Hope this helps! Chris M. (talk) 17:54, 17 February 2010 (UTC)

Least squares and oscillating solutions

Hi all,

I'm running a least squares algorithm for multilateration compensating for error and noise, meaning I have an overdetermined system. The algorithm is on this paper.

Picture

The target is the middle black dot (0.6,0.8) and there are 4 sensors in a square from (0,0) to (1,1). The circles indicate the samples from the sensors, sampled from a normal distribution with mean the distance between the sensor and target and common variance.

In this scenario the solver oscillates between the two solutions $S_{1}$ and $S_{2}$ (after 10,000 iterations at least). I suspect it may be because the fourth circle doesn't intersect with any of the others so there are multiple solutions.

Is there a way to obtain a solution that converges to a single solution when such a scenario arises? Is it even meaningful?

Thanks in advance. x42bn6 Talk Mess 16:29, 16 February 2010 (UTC)

Two possibilities emerge to explain your oscillation: (1) failure to converge for numerical reasons (i.e., incorrectly implemented or inefficiently slow converging LSQR algorithm); and/or (2) failure to converge because of physical problem setup (i.e., actual existence of two global minima).

If you have four receivers, you have an overdefined system. This means you have a null space which defines that set of solutions that are least incorrect - and you are solving for the least squares error. I think the solution should be well-defined - a single, unique point with minimal error. LSQR should be navigating that nullspace to converge at a specific point. One way to tell if the issue is your descent algorithm or your problem formulation is to print the value of the error (residual) at every iteration. Is it decreasing, or is it remaining the same when you iterate up to 10,000 steps? If it continues to decrease, you have a slow convergence, and you might switch to a better solver (such as a conjugate gradient solver). If the residual is not decreasing, you have identified the null-space of your physical problem, and must specify some other stop-condition (e.g. maximum iteration number) or redefine the error-criteria for your physical problem. Sometimes in such source-location-detection problems, your setup is symmetric - meaning that there is an inherent ambiguity between (for example) sources directly in front and sources directly behind your receiver array. Do your S1 and S2 solutions show some kind of physical symmetry like that? Nimur (talk) 17:00, 16 February 2010 (UTC)

Another thing to check - are you using double-precision or single-precision math? In practice, a lot of oscillation and instability is caused by machine roundoff. This can occur even if you have the appropriate accuracy in single-precision to describe your data - but your residual may be inaccurately calculated, screwing the algorithm up. Nimur (talk) 17:02, 16 February 2010 (UTC)

I'm using double-precision, Java doubles. The errors $\|T-c\|$ where c is the current "guess" oscillate between 0.246303038971375.. and 0.253732400873977.. but don't seem to go down or converge. I may have simply programmed it wrong.

Except for these irritating cases I get something which is sensible. A 2D histogram gives a normal distribution-like 3D surface centred about the true position, so I know the algorithm works in some sense. x42bn6 Talk Mess 17:14, 16 February 2010 (UTC)

Hm. I'll take a look at that paper in a little more detail to decipher the algorithm and see if I can't spot an obvious trouble-spot. Have you tried other simulation inputs and obtained the same oscillation? Nimur (talk) 22:50, 16 February 2010 (UTC)

Mathmatical formula for infinity symbol

I have a 3D application that allows me to draw different waveforms with the variables X(t),Y(t), and Z(t). I can also plug numbers into Tmix and Tmax. Based on this, how could I draw a figure-8 infinity symbol? (Googling 'infinity symbol math formula' doesn't give me anything relevant. --70.167.58.6 (talk) 17:51, 16 February 2010 (UTC)

It's called a Lemniscate. Black Carrot (talk) 18:21, 16 February 2010 (UTC)

Mathworld has the parametric equations for one version of the lemniscate. Black Carrot (talk) 18:22, 16 February 2010 (UTC)

Alternate Law of Cosines

1.) c² = a² + b² -2ab cosC,
2.) a² = b² + c² -2bc cosA,
3.) b² = a² + c² -2ac cosB,
Add 2.) and 3.):
a² + b² = a² + b² +2c² -2bc cosA -2ac cosB.
Terms in a² and b² cancel, leaving
2c² -2bc cosA -2ac cosB = 0.
Divide out the common factor 2c and move terms:
4.) c = a cosB + b cosA, similarly:
5.) b = a cosC + c cosA,
6.) a = b cosC + c cosB.

Are not equations 4, 5 and 6 alternative forms of the law of cosines? Should they not be mentioned in the article on that law? —Preceding unsigned comment added by 71.105.162.193 (talk) 17:54, 16 February 2010 (UTC)

I thought the law of cosines was most useful when you knew the lengths of two sides and the angle between them. If you know two sides (WLOG a and b) and two angles (WLOG A and B), then the sine rule is the fastest, using 180°=A+B+C. x42bn6 Talk Mess 18:01, 16 February 2010 (UTC)

Glancing at it for a few seconds, it looks correct. Whether the law of cosines can be deduced from these identities is another question. What else besides that can be deduced from them is yet another; in particular, might one use them in solving triangles or for other purposes? Michael Hardy (talk) 18:14, 16 February 2010 (UTC)

It's that they contain redundant information: If you know e.g. two of the angles A and B you can deduce the third and only need to know one side to work out all the others. Not only is this wasteful (you have to do extra work measuring four things) but is also more complex as how do you deal with e.g. the values not all agreeing because you measure angles better than lengths? You can do extra calculations to be sure they agree, but then you've done at least as much work as the original formula.--JohnBlackburne^words_deeds 18:18, 16 February 2010 (UTC)

Equation 4 can be deduced immediately by drawing the perpendicular from C to c, and similarly for the other equations. But there is a proof of the law of cosines here if you take your derivation in reverse.--RDBury (talk) 00:08, 18 February 2010 (UTC)

In fact this is one of the proofs of the law of cosines given in the article.--RDBury (talk) 00:10, 18 February 2010 (UTC)

Here's another way to derive it. Recall that the law of sines says that

${\sin A \over a}={\sin B \over b}={\sin C \over c},$

so that for some constant d we must have

$d\sin A=a,\quad d\sin B=b,\quad d\sin C=c$

(the constant of proportionality, d, is actually the diameter of the circumscribed circle, but we won't need that fact here). So then

$a\cos B+b\cos A=d\left(\sin A\cos B+\sin B\cos A\right)=d\sin(A+B),\,$

and since A + B + C = half-circle, it follows that sin(A + B) = sin(C). Consequently

$a\cos B+b\cos A=d\sin(A+B)=d\sin C=c,\,$

and hence

$a\cos B+b\cos A=c.\,$

Michael Hardy (talk) 23:53, 16 February 2010 (UTC)

One last question on principal ideals

Hi there everyone,

Another one from me, this is my last question on Ring theory for the fortnight (hooray) and it's a toughie unfortunately.

Let F be a field, and let R=F[X,Y] be the polynomial ring in 2 variables. i) Let I be the principal ideal generated by the element X-Y in R. Show $R/I\cong F[x]$ ii) What can you say about R/I when I is the principal ideal generated by $X^{2}+Y$? iii) [Harder] What can you say about R/I when I is the principal ideal generated by $X^{2}-Y^{2}$?

The first was fine, I used the isomorphism theorem for rings with the homomorphism taking f(x,y) to f(x,x), which has kernel (X-Y), and for the second I took the same approach, setting f(x,y)=f(x,-x^2) - I got the same solution as (i), is that right? It's the third part of the question I'm having the problems with, since obviously we can't just set $x^{2}=y^{2}$, because that has ambiguities, and x=y or x=-y aren't valid either. Could anyone suggest what I should do to evaluate R/I in this case?

Thanks very much all :) 82.6.96.22 (talk) 21:43, 16 February 2010 (UTC)

You'll have to decide what you mean by "evaluating" R/I. It's certainly not isomorphic to k[x]. Try writing down a basis for R/I as an F-vector space, that might give you a feel for what the ring is like Tinfoilcat (talk) 23:27, 16 February 2010 (UTC)

Well, if I could find an obvious analogue to F[x] to which R/I would be isomorphic, then that would be great, but I'm not sure whether one actually exists - I'll try and fathom out a basis and see if I can get anywhere with it. 82.6.96.22 (talk) 08:28, 17 February 2010 (UTC)

(Consider the following in the context of (iii); it may provide a different way of analyzing the problem) Let $p(X,Y)=X+Y$ and let $q(X)=X-Y$, and consider the cosets $r=p(X,Y)+I$ and $s=q(X,Y)+I$ in $F[X,Y]/(X^{2}-Y^{2})$. Note that $rs=0$, ${\frac {r+s}{2}}=X$, and ${\frac {r-s}{2}}=Y$. Consider the ring $F[X,Y]/(XY)$. PST 11:08, 17 February 2010 (UTC)

In other words, use the ring version of the Chinese remainder theorem.—Emil J. 12:26, 17 February 2010 (UTC)

It's not really the CRT, which only applies if the two ideals are coprime. There's something slightly different going on though: what you get, as PST observes, is a fibre product (pullback). This example should be an instance of a more general result about fibre products, something like: let R be a ring with max ideal m such that R/m=F. Let I,J be ideals such that I+J=m. Then R/IJ is iso to the fibre product of R/I and R/J 129.67.37.143 (talk) 21:16, 17 February 2010 (UTC)

LaTeX question, columns

I want to type up a list of derivatives and integrals, just like the table that is in the front or back cover of a lot of calculus textbooks. That is, a one page sheet, one-sided sheet with just the standard derivatives and integrals, up through arcsine and such, but not hyperbolic functions and their inverses. Any way, what I have in mind is Derivatives on top with 2 columns and then Integrals on the bottom half with 2 columns. Does any one know a good way to do this? I used something called "multicols" but it doesn't line up well. That is, if some formula is taller than others, the two columns don't line up well. I want 1. to be in the exact same vertical position as 10 (or whatever number), then 2 and 11, 3 and 12, and so on. Any help would be appreciated. Thanks. NumberTheorist (talk) 22:29, 16 February 2010 (UTC)

Hmm, I guess I could just do a table. That might work nicely and it's simple. Well, if you have any great ideas, I'd love to hear them but otherwise I'll just do a table. NumberTheorist (talk) 22:50, 16 February 2010 (UTC)

I am not sure why you'd want to align rows exactly, especially if the formulas had very different heights, but that is your call. A table would do that. You can always permute the formulas to approximately match heights within each row. Baccyak4H (Yak!) 19:25, 17 February 2010 (UTC)

It's not that they have very different heights. It's that they have slightly different heights and most are a standard height. But, with multicols, a few with slightly different heights adds up and then the rows aren't lined up well at all. Also, in this case, I want the formulas in a certain order that makes sense, like all the trig derivatives will be in a group at the bottom and sin and cos go first as far as those go, and other things like this. I think a table is a perfect idea and I don't know why I didn't think of it sooner. NumberTheorist (talk) 20:52, 17 February 2010 (UTC)

Depending on what exactly you are going for the AMS-math "align" environment might work also. Although it's generally used for lining up a single column of equations, it supports multiple columns as well. See Wikipedia:Reference desk/Archives/Mathematics/2009 September 7 for an example. Eric. 131.215.159.171 (talk) 23:39, 17 February 2010 (UTC)

February 17

Proof for this example on the Lambert W function?

The Lambert W function has several examples, but only has proof for the first one.

Does anyone have a proof for example 3? —Preceding unsigned comment added by Luckytoilet (talk • contribs) 05:05, 17 February 2010 (UTC)

By continuity of exponentiation, the limit c satisfies c = z^c = e^{c log z}. Rearranging it a bit gives (−c log z)e^{−c log z} = −log z, thus W(−log z) = −c log z, and c = W(−log z)/(−log z). Not quite sure why the example talks about the "principal branch of the complex log function", the branch of log used simply has to be the same one as is employed for the iterated base-z exponentiation in the definition of the limit. Also, note that the W function is multivalued, but only one of its values can give the correct value of the limit (which is unique (or nonexistent) once log z is fixed).—Emil J. 15:04, 17 February 2010 (UTC)

Follow up: the name for the argument of the logarithmic function

When reading the exponential term a^x, one can say "exponentiation - of a - to the exponent n". However, one can also use the explicit name "base" for a, and say: "exponentiation - of the base a - to the exponent n". My question is about whether one can also use any explicit name for x - when reading the logarithmic term log_ax, i.e. by saying something like: "logarithm - of the blablabla x - to the base a"... HOOTmag (talk) 08:02, 17 February 2010 (UTC)

I would reckon a correct term would be argument (but this is quiet general as it would apply to any such function/monomial operator). Also note it would most likely be read as "logarithm base a of the argument x" A math-wiki (talk) 08:56, 17 February 2010 (UTC)

• Why have you posted this again? There is an ongoing discussion above. I suggest that the term for the argument of log is just argument and that it's most sensible to say "the logarithm of x to the base a". Why much there be a technical term? —Anonymous Dissident^Talk 09:01, 17 February 2010 (UTC)

@A math-wiki, @Anonymous Dissident: Sorry, but just as the function of exponentiation has two arguments: the "base", and the "exponent", so too does the function of logarithm have two arguments: the "base", and the other argument (whose name is still unknown), so I can't see how the term "argument" may solve the problem, without a confusion. The problem is as follows: does the function of logarithm have a technical term for the second argument (not only for the first one), just as the function of exponentiation has a technical term for the second argument (not only for the first one)? HOOTmag (talk) 14:27, 17 February 2010 (UTC)

I believe you have got your answer. No it has no special name that anyone here knows of. The closest you'll come to a name is argument. Dmcq (talk) 15:05, 17 February 2010 (UTC)

If you've read my previous section, you've probably realized that the term "argument" can't even be close to answering my question. Also note that I didn't ask whether "it has a special name that anyone here knows of", but rather whether "it has a special name", and I'll be glad if anybody here know of such a name, and may answer me by "yes" (if they know that there is a special name) or by "no" (if they know that there isn't a special name). HOOTmag (talk) 17:50, 17 February 2010 (UTC)

Er, the "that anyone here knows of" part is inherent in the process of answering questions by humans. People cannot tell you about special names that they do not know of, by the definition of "know". If you have a problem with that, you should ask at the God Reference Desk rather than the Wikipedia Reference Desk.—Emil J. 18:02, 17 February 2010 (UTC)

If you answer me "I don't know of a special name", then you've replied to the question "Do you know of a special name". If you answer me: "Nobody here knows of a special name", then you've replied to the question: "Does anyone here know of a special name". However, none of those questions was my original question, since I'm not interested in knowing whether anyone here knows of a special name, but rather in knowing whether there is a special name. I'll be glad if anybody here know of such a name, and may answer me by: "yes, there is" (if they know that there is a special name) or by: "no, there isn't" (if they know that there isn't a special name). HOOTmag (talk) 18:22, 17 February 2010 (UTC)

No one can positively know that there isn't a name. You can't get a better answer than what Dmcq wrote (unless, of course, there is such a name after all).—Emil J. 18:33, 17 February 2010 (UTC)

I can positively know that there is a special name for each argument of the function of exponentiation (the special names are "base" and "exponent"), and I can also positively know that there isn't a special name for the argument of functions having exactly 67 elements in their domain. HOOTmag (talk) 18:49, 17 February 2010 (UTC)

Trying to dictate to a reference desk how they should reply to you is not a good idea if you want answers to further questions. Dmcq (talk) 19:44, 17 February 2010 (UTC)

Dictate? never! I've just said that any answer like "Nobody here knows of a special name" - doesn't answer my original question, which was not: "Does anyone here know of a special name", but rather was: "Is there a special name". As I've already said: "I will be glad if anybody here know of such a name, and may answer me by 'YES' (if they know that there is a special name) or by: 'NO' (if they know that there isn't a special name)".

Note that - to be "glad" - doesn't mean: to try to dictate... HOOTmag (talk) 20:31, 17 February 2010 (UTC)

Ah, but there is a special name for the argument of a function that has exactly 67 elements in its domain. Such an argument is called a "septensexagesimand." Erdős used the term in "On the edge-couplet hyperpartitions of uniregular antitransitive trigraphs," J. Comb. Omni. Math. Acad. 61(3):1974, 201–212. —Bkell (talk) 22:26, 17 February 2010 (UTC)

When you review the article you see that the name was slightly different: "trisexagesimand", and that it was for 63 elements only. As for 67 elements, I know for sure that there's no special name. HOOTmag (talk) 08:27, 18 February 2010 (UTC)

Oops, sorry, my mistake. —Bkell (talk) 09:00, 18 February 2010 (UTC)

In an attempt to answer your question in an acceptable manner, I will first note that I (like everyone else here) have never heard a special term for this, but just taking a stab in the dark I searched for "logarithmand" and found that this word has apparently been used at least once in history (though many of the results seem to be false positives resulting from the phrase "logarithm and"). In particular, Martin Ohm used the word in his 1843 book The spirit of mathematical analysis: and its relation to a logical system. So there you are. —Bkell (talk) 09:37, 18 February 2010 (UTC)

Here are some more usages of the term: George Peacock, 1842, A treatise on algebra; Hermann Schubert and Thomas J. McCormack, 1898, Mathematical Essays and Recreations (in which is also offered the technical term "number"; see also the Project Gutenberg edition); and the German Wikipedia entry on Logarithmus. —Bkell (talk) 09:53, 18 February 2010 (UTC)

That was quite some stab in the dark, congratulations. I guess that's why my wife is better at crosswords than me :) Dmcq (talk) 11:03, 18 February 2010 (UTC)

By the way if you like that I'm sure you'll like logarithmancy which is divination using Napier's logarithm tables Dmcq (talk) 11:14, 18 February 2010 (UTC)

Hahaha… And logarithmandering, the establishment of political boundaries so as to resemble a nautilus shell? —Bkell (talk) 11:27, 18 February 2010 (UTC)

Oh, wait, you were serious—logarithmancy is actually a real thing. Well, whaddya know. —Bkell (talk) 11:30, 18 February 2010 (UTC)

Thank you, Bkell, for your discovery! I appreciate that! I think it's a good idea to add this information to the English Wikipedia, (in logarithm). HOOTmag (talk) 12:31, 18 February 2010 (UTC)

I doubt it is of current interest and wikipedia isn't a dictionary. But it should go in wiktionary I guess if that other word is there. Dmcq (talk) 12:38, 18 February 2010 (UTC)

As Bkell has pointed out, it is - already - in the German Wikipedia. HOOTmag (talk) 12:54, 18 February 2010 (UTC)

The use in German has no relevance. Dmcq (talk) 13:12, 18 February 2010 (UTC)

The use of this term is not just in German, it's in English too, as appearing in the sources Bkell indicated. I mentioned the German Wikipedia - not for showing the German term (since it's a universal term) - but rather for showing that the very information about the special (universal) name for the argument of logarithm appears in other wikipedias as well (not only in wiktionaries). HOOTmag (talk) 13:44, 18 February 2010 (UTC)

I question your claim that it's a "universal" term. As far as I can see, the term is primarily used in German; the only sources we have in English are from the 19th century, two of which were written by German authors (one of them in the German language, so the translator, lacking an English equivalent, probably just kept the German word) and the last of which only mentions it in a footnote and cites a German work. Yes, it has been used in English, but it is extraordinarily rare and seems to have failed to gain acceptance in any significant way. —Bkell (talk) 13:53, 18 February 2010 (UTC)

In fact, for what it's worth, during my brief explorations trying to find a term for the argument of the logarithm function, I found more sources that called it the "number" than that called it the "logarithmand" (this includes two of the four sources I gave for "logarithmand"). So if you're going to mention that the argument is sometimes called the logarithmand, you should be honest and also say that it is more commonly called the "number" and even more commonly not called anything at all. —Bkell (talk) 14:00, 18 February 2010 (UTC)

According to your treatise, the first auther to have used this term is George Peacock (in "A treatise on algebra", 1842), right? His name doesn't sound German... HOOTmag (talk) 14:07, 18 February 2010 (UTC)

Did you read that link? The term appears in a footnote that ends with, "See Ohm's Versuch eines vollkommen consequenten system der mathematick, Vol. 1." That's why I said, "…the last of which only mentions it in a footnote and cites a German work." —Bkell (talk) 14:13, 18 February 2010 (UTC)

Even the German wikipedia says it isn't used nowadays. Dmcq (talk) 15:36, 18 February 2010 (UTC)

First/second order languages

1. How should we call a first/second order language, whose all symbols are logical (like connectives quantifiers variables and brackets and identity), i.e. when it contains neither constants nor function symbols nor predicate symbols (but does contain the identity symbol)?

1. If a given open well-formed formula contains signs of variables ranging over individuals, as well as signs of variables ranging over functions, while all quantifications are used therein over variables ranging over individuals only (hence without quantifications over variables ranging over functions), then: is it a first order formula, or a second order formula?

Note that such open formulae can be used (e.g.) for defining correspondences (e.g. bijections) between classes of functions (e.g. by corresponding every invertible function to its inverse function).

HOOTmag (talk) 17:53, 17 February 2010 (UTC)

I'm a novice so I'm not sure if my answers are correct. Your 1st question: if there are no predicate symbols, there would be no atomic formulas and hence no wfs. Your 2nd question: it a second order formula because first order can only have variables over the universe of discourse. Your note: I think function are coded as sets in set theories, hence defining a bijection would be a 1st order formula because variables/quantifies are over sets (the objects in our domain). Money is tight (talk) 18:12, 17 February 2010 (UTC)

There are plenty of formulas in languages without nonlogical symbols. In first-order logic, apart from $\bot$, $\top$ (if they are included in the particular formulation of first-order logic) you have also atomic formulas using equality, and therefore the language is sometimes called the "language of pure equality". In second-order logic, there are also atomic formulas using predicate variables. One could probably call it the language of pure equality as well, but there is little point in distinguishing it: any formula in a richer language may be turned into a formula without nonlogical symbols by replacing all predicate and function symbols with variables (and quantifying these away if a sentence is desired). As for the second question, the formula is indeed a second-order formula, but syntactically it is pretty much indistinguishable from the first-order formula obtained by reinterpreting all the second-order variables as function symbols.—Emil J. 18:28, 17 February 2010 (UTC)

Sorry, but I couldn't figure out your following statement:

• any formula in a richer language may be turned into a formula without nonlogical symbols by replacing all predicate and function symbols with variables (and quantifying these away if a sentence is desired).

Realy? If I use a richer language, containing a function symbol - which (in a given model) receives a colour and returns it's negative colour, so how can I replace that function symbol by a function variable without losing my original interpretation for the function?

HOOTmag (talk) 13:02, 18 February 2010 (UTC)

A language is entirely syntactic, it does not include an interpretation, which is a separate matter. Emil is saying that the formula "a - b" can be viewed either as a first-order formula with a function symbol "-" and free variables a and b, or as a second-order formula with variables a and b of type 0 and a free variable "-" of higher type. The formula, being just a string of symbols, does not know whether "-" is meant to be a function symbol or a function variable. The same holds for the "=" predicate, actually. — Carl (CBM · talk) 13:36, 18 February 2010 (UTC)

The atomic formula "x=x" has no non-logical predicate symbols (note that the identity sign is logical): all of its symbols are logical (including the symbol of identity)

Note that the universe of discourse is the set of individuals and of functions ranging over those individuals.

HOOTmag (talk) 18:35, 17 February 2010 (UTC)

A first order theory with equality is one that has a predicate symbol that also has axioms of reflexivity and substitutivity. I'm not sure why you say x=x has no non logical symbols. Clearly the only logical connectives are for all, there exist, not, or, and, material implication. And the universe of discourse only contains the individuals D in our question, not functions with domain D^n. The functions are called 'terms', which are used to build atomic formulas and then wfs. Money is tight (talk) 18:43, 17 February 2010 (UTC)

In first-order logic with equality, the equality symbol is considered a logical symbol, the reason being that its semantics is fixed by the logic (in a model you are not allowed to assign it a binary relation of your choice, it's always interpreted by the identity relation). Anyway, the OP made it clear that he intended the question that way, so it's pointless to argue about it.—Emil J. 19:24, 17 February 2010 (UTC)

@Money is tight: Your comment regarding the domain of discourse is correct. Sorry for my mistake. HOOTmag (talk) 13:13, 18 February 2010 (UTC)

The contents of the domain(s) of discourse will depend on what semantics are used. See second-order logic for an explanation. — Carl (CBM · talk) 13:24, 18 February 2010 (UTC)

Note that in higher-order languages for arithmetic, equality of higher types is very often not taken as a logical symbol.

In the context of higher-order arithmetic, a formula with no higher-order quantifiers (but possibly higher-order variables) is called "arithmetical". For example, the formula $\exists n(F(n)=0)$ is an arithmetical formula with a free variable F of type 0→0.

As for "first-order languages" versus "second-order languages", this distinction breaks down upon closer inspection. One cannot tell which semantics are being used merely by looking at syntactic aspects of a formula, and so the very same syntactical language can be both a first-order language and a second-order language. The language of the theory named second-order arithmetic is an example of this: the usual semantics for this theory are first-order semantics, and so in that sense the language is a first-order language (with two sorts).

However, classical usage has led to several different informal meanings for "higher-order language" in the literature, which are clear to experts but not formally defined. — Carl (CBM · talk) 13:23, 18 February 2010 (UTC)

Homomorphism

I'm looking for two homomorphisms f:S2->S3, g:S3->S2 such that the composition gf is the identity on S2 (the S means the 2nd and 3rd symmetric groups). Does two such homomorphism exist? I know everything is finite so I can brute force my way but I don't like that approach. Thanks Money is tight (talk) 18:00, 17 February 2010 (UTC)

If gf is the identity, then g is a surjection. Thus its kernel must be a normal subgroup of index 2. Can you find one? This will give you g, and then constructing the matching f should be easy.—Emil J. 18:14, 17 February 2010 (UTC)

Perhaps I am confused; wouldn't the kernel of g need to have index 3? Eric. 131.215.159.171 (talk) 23:21, 17 February 2010 (UTC)

Yes, you're confused. The index of the kernel is the same as the order of the image. Perhaps you're confusing index with order? Algebraist 23:24, 17 February 2010 (UTC)

You're right, I am confused. My thoughts were S2 has order 2, S3 has order 6, so "index" is 3... oops. Eric. 131.215.159.171 (talk) 00:29, 18 February 2010 (UTC)

It may be helpful to analyze this problem more generally: For which m and n do there exist homomorphisms $f:S_{n}\to S_{m}$ and $g:S_{m}\to S_{n}$ such that the composition $gf$ is the identity on $S_{n}$? If you use EmilJ's method, you should solve this general problem; however, it might also be necessary to precisely determine the normal subgroups of $S_{x}$ for all natural x (and this is not too hard to do if you are equipped with the right theorems). PST 01:10, 18 February 2010 (UTC)

Let H be the subgroup consisting of e, k1, k2, where e is the identity and k1 k2 are the two elements with each other as inverse (for example k1 is the function f(1)=2, f(2)=3, f(3)=1). I think this is the subgroup EmilJ is to talking about. Now map everything in H to the identity i in S2, and the rest to the other element in S2. I think this is a homomorphism g. Then define f to be the map that sends i to e and the other element in S2 to one of the three elements in S3 with itself as inverse. Correct? Money is tight (talk) 06:09, 18 February 2010 (UTC)

Correct. You might like to see the article alternating group; every non-trivial permutation group $S_{n}$ has a unique subgroup of index 2, and this is referred to as the alternating group $A_{n}$ (perhaps more concretely, an element of $S_{n}$ is in $A_{n}$ if and only if it is the product of an even number of transpositions). Using your notation, the alternating subgroup $A_{3}$, the unique subgroup of $S_{3}$ with index 2, is simply $\{e,k_{1},k_{2}\}$. There are other useful results about alternating groups that can help you to solve generalizations of this problem; for instance, $A_{n}$ is normal in $S_{n}$ for all natural n (since, of course, any subgroup of index 2 in a group must be normal). Therefore, if we define $g:S_{n}\to S_{2}$ by setting g to be the identity of $S_{2}$ for all elements in $A_{n}$, and the (unique) non-identity element of $S_{2}$ for all elements outside $A_{n}$, g is a homomorphism on $S_{n}$ with kernel $A_{n}$. If we define $f:S_{2}\to S_{n}$ by setting f to be an element of order 2 outside $A_{n}$ on the (unique) non-identity element of $S_{2}$, and the identity element of $S_{n}$ on the identity of $S_{2}$, f is also a homomorphism and $gf$ is the identity on $S_{2}$. In case you are studying permutation groups at the moment (are you?), you might find this interesting. PST 08:49, 18 February 2010 (UTC)

You are probably already aware of this, but it may also help to explicitly write down the elements of $S_{3}$: $S_{3}=\{e,(123),(132),(12),(13),(23)\}$ where we use cycle notation to describe the individual elements. Of course, this will become too cumbersome should we investigate higher order permutation groups, and thus the above method (described by EmilJ) is more appropriate. PST 08:58, 18 February 2010 (UTC)

Ominus

What's the conventional meaning and usage of the symbol encoded by the LaTeX markup "\ominus"? (i.e. $\ominus$). There doesn't currently seem to be a ominus Wikipedia page yet. -- 140.142.20.229 (talk) 18:50, 17 February 2010 (UTC)

Mainly this: if $X\subset Y$ are closed linear subspaces of a Hilbert space, $Y\ominus X$ denotes the orthogonal subspace $Z$ of $X$ relative to $Y$, that is $Z:=Y\cap X^{\perp }$. It comes of course from the notation for the orthogonal sum, $Y=X\oplus Z.$ As you see, it doesn't seem so theoretically relevant to deserve an article of its own; but as a notation is nice and of some use. --pma 19:08, 17 February 2010 (UTC)

It is also used in loads of other places like removing parts of a graph or when reasoning about computer floating point where there is a vaguely subtraction type of operator and the person wants a symbol for it. Basically a generally useful extra symbol. Dmcq (talk) 19:36, 17 February 2010 (UTC)

Note that "ominus" isn't meant to be a single word; it's meant to be read as "O minus", suggesting a minus sign within an O. Likewise there are \oplus $\oplus$, \otimes $\otimes$, \odot $\odot$, etc. The official term for the symbol, if there is one, is probably something like "circled minus sign"; but \ominus is shorter to type, and that's what Knuth called it when he wrote TeX. —Bkell (talk) 07:47, 18 February 2010 (UTC)

The respective Unicode 5.2 character code chart Mathematical Operators calls it "CIRCLED MINUS" (code point 2296_hex). —Tobias Bergemann (talk) 09:27, 18 February 2010 (UTC)

Spherical harmonic functions

I'm looking for the normal modes of a uniform sphere. I have a classic text on solid mechanics, by A. E. H. Love, but I can't quite make sense of the math. He gives a formula for the mode shape in terms of "spherical solid harmonics" and "spherical surface harmonics," which he uses and discusses in a way that doesn't seem to match Wikipedia's description of spherical harmonics. Can you help me identify these functions? The following facts seem to be important:

• The general case of a "spherical solid harmonic" is denoted $V_{n}$. Note the presence of only one index, rather than two.
• $V_{n}(r,\theta ,\phi )=r^{n}S_{n}(\theta ,\phi )$, where $S_{n}$ is a "spherical surface harmonic." I would expect S to be equivalent to Y, except that it's missing one index.
• Unlike the regular spherical harmonics Y, the "spherical solid harmonics" V apparently come in many classes, three of which are important to his analysis and denoted $\omega _{n}$, $\phi _{n}$, and $\chi _{n}$. The description of the distinction between these classes makes zero sense to me.
• Several vector-calculus identities involving V are given. I can type these up if anyone wants to see them.

Does anyone know what these functions V or S are? --Smack (talk) 18:59, 17 February 2010 (UTC)

S is surely just Y with $n\equiv \ell$ and the m index suppressed (perhaps azimuthal variations are less important here?), which makes V a (regular) solid harmonic R with the same index variations. I don't know what the classes of solid harmonics are supposed to be, unless he's denoting the different values of m as different classes (0 and ±1, or 0/1/2?). --Tardis (talk) 20:51, 17 February 2010 (UTC)

Thanks; that answers my question except for the problem of the missing m index. I can't see why azimuthal variation would be less important, since the subject is the mechanics of a sphere. Thinking out loud for a minute, I can come up with the following possibilities:

• According to your guess, the three classes correspond to m = 0, ±1, ±2. In this case, I would expect to find an equation using ω, and be able to substitute φ or χ to get a different mode. However, the mode shape equation uses both ω and φ, which makes substitution difficult.
• m can take any arbitrary value ($\leq n\equiv \ell$). This makes no sense in light of the frequency equation, which has n all over it (as it should), but does not use any other index (which it also should).
• m is fixed to a single value, most likely $m=0$ or $m=n$. This would be silly in a text claiming to discuss all of the modes of a sphere. (The original work was published in 1882. Surely both indices of the Y function had been discovered by then?)

--Smack (talk) 22:34, 17 February 2010 (UTC)

math conversion two

is there a website where I can convert litre into mililitre, convert litre into pint, convert into gallon, convert litre into kilogram, litre into decalitre and such? —Preceding unsigned comment added by 74.14.118.209 (talk) 20:22, 17 February 2010 (UTC)

Google will do most of that for you, e.g. type "2 litres in pints". Litre to kilogram though would be dependent on the density of what you are measuring. Note that some of your conversions are simply multiplication or division based on the prefix (litre to millilitre, for example). --LarryMac | Talk 20:32, 17 February 2010 (UTC)

For anything beyond Google's capabilities, check out Online Conversion. --Smack (talk) 22:36, 17 February 2010 (UTC)

Be aware that there are different kinds of pints, gallons, etc. Google assumes by default that you want US liquid measure; if you want Imperial, you have to say "2 liters in imperial pints" or similar. Or perhaps this depends on what country it thinks you are in. Similar issues arise with other units, such as tons. --Anonymous, 06:19 UTC, December 18, 2010.

No need to go to a website. Just pull up an xterm and run units. 58.147.58.28 (talk) 10:21, 18 February 2010 (UTC)

Minkowski paper on L1 distance

I know that L1 distance is often referred to as Minkowski distance. I'm trying to find out where (in which paper/book) did Minkowski introduce L1 distance. I can only find many references stating that he introduced the topic, but no references to a specific paper or book. Does anyone here know the name of the paper/book? -- kainaw™ 20:59, 17 February 2010 (UTC)

Looked around, and also found it was a frustrating question to find out directly, could only find at best references to his collected works, implying a trip to the library, sooo second millennium. So guess/vague memory that it was from his Geometry of numbers led to this nice paper or [5], with this ref: H. Minkowski, Sur les propriétés des nombres entiers qui sont dérivées de l’intuition de l’espace, Nouvelles Annales de Mathematiques, 3e série 15 (1896), Also in Gesammelte Abhandlungen, 1. Band, XII, pp. 271–277. Also mentions that Riemann mentioned L4 in his famous Habilitationsschrift.John Z (talk) 01:55, 19 February 2010 (UTC)

Thanks. I also went to the library and was directed to a German copy of "Raum und Zeit", which appears to be a collection of his talks on L-space. I found a German copy online and used Babelfish to make sense of it - which wasn't too bad considering it is a physics/math book. -- kainaw™ 02:00, 19 February 2010 (UTC)

Thanks again - the history section of that first paper is great. -- kainaw™ 02:02, 19 February 2010 (UTC)

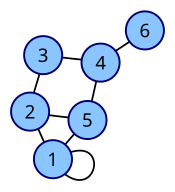
LaTeX matrices

In this figure there would have $a_{1},a_{2},a_{3}$ instead of the red and blue arrows.

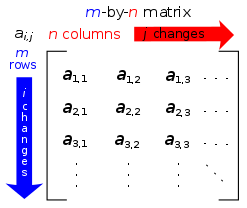
Is there any way of creating matrices in LaTeX where you display the name of each individual row and column on the left and top of the matrix respectively? Drawing an adjacency matrix would look something like this:

Labeled graph	Adjacency matrix
	${\begin{pmatrix}1&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{pmatrix}}$

only with $1,2,3,4,5,6$ on the top of the matrix and the same on it's side- because the matrix doesn't say which vertices of the graph relates to which row or column in it's current state. Is this an odd request? I could have sworn I've seen people do this (especially when the names of the vertices are odd) --BiT (talk) 21:46, 17 February 2010 (UTC)

One way to do something somewhat similar:

$M:{\begin{array}{c|c|c|c|c|c|}1&2&3&4&5&6\\\hline 1&1&2&3&4&5\\\end{array}}$

or in two dimensional case:

$M:{\begin{array}{c|c|c|c|c|c|}&1&2&3&4&5\\\hline 1&1&2&3&4&5\\\hline 2&1&2&3&4&5\\\hline 3&1&2&3&4&5\\\hline \end{array}}$

It only looks reasonably nice in case of a one-dimensional array, but it's still better than nothing... --Martynas Patasius (talk) 22:57, 17 February 2010 (UTC)

In plain TeX there is a macro called \bmatrix \bordermatrix that will do what you want. Searching for latex bordermatrix will hopefully lead you to something. —Bkell (talk) 07:53, 18 February 2010 (UTC)

Thank you very much Bkell, that was exactly what I was looking for. --BiT (talk) 15:29, 18 February 2010 (UTC)

Integral of 1/x

User:Daqu mentioned a problem with the usual expression for the real number integral of 1/x on the page Talk:Range (mathematics). The usual answer is

$\int {1 \over x}\,dx=\ln \left|x\right|+C$

The problem I see is if someone integrates over an interval including 0. Should one just say the value is indeterminate, use the complex logarithm, or just accept that people might come up with 0 when integrating between −1 and +1? after all one might consider the two areas as canceling even if they are both infinite! Has anyone seen a book that actually mentions this problem? Dmcq (talk) 22:44, 17 February 2010 (UTC)

You can't integrate right through 0 even in the complex case, I'm pretty sure, at least without getting into careful analysis of what kind of integral you mean (e.g. the Henstock-Kurzweil integral might be able to handle it). Of course the contour integral is well-defined for any other path, with the Cauchy integral formula describing what happens for closed loops around the origin. 66.127.55.192 (talk) 23:47, 17 February 2010 (UTC)

Technically the above formula is an indefinite integral and really all it says is that the derivative of $\ln \left|x\right|$ is $1 \over x$, with the restriction x ≠ 0 implicit from the domains of the functions involved. What you're really saying is that there is a problem when you try to apply the fundamental theorem of calculus with this formula, but the conditions required for the FTC would eliminate cases where the interval of integration is not a subset of the domain, as would be the case here. So actually everything is correct here but if I was teaching a calculus class I would be careful to point out to students that due care is needed when applying this formula.--RDBury (talk) 00:00, 18 February 2010 (UTC)

So just add a warning about not integrating at 0, sounds good to me. Thanks Dmcq (talk) 01:01, 18 February 2010 (UTC)

One of the basic properties of the Henstock–Kurzweil integral is that whenever $\int _{a}^{b}f(x)\,dx$ exists, then $\int _{c}^{d}f(x)\,dx$ exists for any a ≤ c ≤ d ≤ b as well. Thus 1/x is not Henstock–Kurzweil integrable over any interval containing 0. As far as I can see, the only way to make the integral converge is to use the Cauchy principal value.—Emil J. 13:50, 18 February 2010 (UTC)

Is it an indefinite integral? At the freshman level, one makes no distinction between indefinite integrals and antiderivatives, but is that the right level for the context? Michael Hardy (talk) 04:03, 18 February 2010 (UTC)

The integral in question does have a Cauchy principal value.

I have an issue with the assertion that

$\int {dx \over x}=\ln |x|+C,$

if that is taken to identify all antiderivatives. It should say

$\int {dx \over x}=\ln |x|+{\begin{cases}A&{\text{if }}x>0;\\B&{\text{if }}x<0.\end{cases}}$

Michael Hardy (talk) 03:59, 18 February 2010 (UTC)

Farly old problem solved before infinitesimals were such a problem. inf-inf=indeterminate or which infinity is greater? The area under 1/x where x<0 or the area under 1/x where x>0? See [[6]] —Preceding unsigned comment added by 68.25.42.52 (talk) 15:34, 18 February 2010 (UTC)

As I said, there's a Cauchy principal value in this case. And it's 0. Michael Hardy (talk) 03:10, 19 February 2010 (UTC)

Thanks. I've put something at Lists_of_integrals#Integrals_of_simple_functions based on that to see the reaction but I would like a citation. Dmcq (talk) 14:02, 23 February 2010 (UTC)

Consistency of arithmetic Mod N

The consistency of ordinary arithmetic has not yet been satifactorily settled. What is the upper limit for N such that arithmetic modulo N is known to be consistent? Count Iblis (talk) 23:55, 17 February 2010 (UTC)

(Sorry, messed up the page history somehow. Eric. 131.215.159.171 (talk) 00:01, 18 February 2010 (UTC))

I think you need to specify what framework you want to consistency to be proven within. However, if you can prove it for any N I would expect you can prove it for all N. --Tango (talk) 00:03, 18 February 2010 (UTC)

Arithmetic mod N has a finite model so in principle you can check the axioms against it directly. Whether the consistency of arithmetic is settled is of course subject to debate, but Gentzen's consistency proof (using what amounts to structural induction on formulas, don't flip out at the term "transfinite induction" since there are no completed infinities involved) and Gödel's functional proof (which does use infinitistic objects of a limited sort) are both generally accepted. 66.127.55.192 (talk) 01:15, 18 February 2010 (UTC)

You didn't specify what axiom system for arithmetic modulo n you have in mind, and you didn't specify the power of your metatheory. As for the axiomatization, Th(A) is finitely axiomatizable for any finite model A in a finite language, so let me just assume that you fix any finite complete axiomatization Z_n of Th(Z/nZ) in the (functionally complete, in this case) language of rings (the particular choice of the axioms does not matter, since the equivalence of two finitely axiomatized theories is a $\Sigma _{1}^{0}$-statement, and is thus verifiable already in Robinson arithmetic whenever it is true).

Now, what metatheory suffices to prove the consistency of Z_n? In the case n = 2, Z₂ is a notational variant of the quantified propositional sequent calculus, hence questions on its consistency strength belong to propositional proof complexity. The answer is that its consistency is known to be provable in Buss's theory $U_{2}^{1}$. The proof basically amounts to constructing a truth predicate for QBF, which in turn relies on the fact that the truth predicate is computable in PSPACE. Now, exactly the same argument applies to any fixed finite first-order structure, such as Z/nZ. Thus, $U_{2}^{1}$ proves the consistency of Z_n for every fixed n. $U_{2}^{1}$ is a variant of bounded arithmetic, and as such it is interpretable on a definable cut in Robinson's arithmetic Q; thus the consistency proof is finitistic even according to strict standards of people like Nelson. And, in case it is not obvious from the above, the consistency of arithmetic modulo n for each n has nothing to do with the consistency of Peano arithmetic.—Emil J. 15:06, 18 February 2010 (UTC)

I should also stress that conversely, the power of $U_{2}^{1}$ (or a similar PSPACE theory) is more or less required to prove the consistency of Z_n. More precisely, if T is any first-order theory which has no models of cardinality 1 (such as Z_n), then over a weak base theory the consistency of T implies the consistency of the quantified propositional sequent calculus, which in turn implies all $\forall \Sigma _{0}^{b}$-sentences provable in $U_{2}^{1}$ (note that consistency statements are themselves $\forall \Sigma _{0}^{b}$).—Emil J. 16:10, 18 February 2010 (UTC)

February 18

Standard Deviation and Semi-Interquartile Range

Hello. How can I prove that a set of data cannot have a standard deviation smaller than its semi-interquartile range? Thanks in advance. --Mayfare (talk) 10:47, 18 February 2010 (UTC)

What you want is the Law of total variance. To get the minimum standard deviation you want as small a variance as possible on both sides of the medians giving the interquartile range. Which means you need to bunch each side to a single point so you have values only at -x 0 and +y, this quickly works out to needing values only at -x 0 and +x for the minimum standard deviation compared to the semi interquartile range. Dmcq (talk) 11:34, 18 February 2010 (UTC)

I followed the link to see if it confirmed my interpretation of the assertion that the question implies, but am still unsure. Is it true that, for any data set, the standard deviation is equal to or greater than half of the interquartile range? --NorwegianBlue ^talk 19:32, 19 February 2010 (UTC)

Actually it is false. Try it out with just over a quarter of the values at -1, the same amount at +1 and just under half the total at 0. The interquartile range is 2. The semi-interquartile range is 1. The standard deviation is sqrt((-1)²*1/4+0*1/2+1²*1/4) = 1/sqrt(2) which is less than 1. Dmcq (talk)

Alternation Operator

Hello. I'm currently reading a book on manifolds and I've gotten confused by a really simple exercise, or I'm missing something. The book defines an action for permutations of k symbols on k-linear maps via pF(v1,...vk) = F(vp(1),...vp(k)). It, then, defines Alt f = the sum of all terms sgn(p)(pf), where p ranges over the symmetric group. The exercise is to consider Alt f in the case that f is 3-linear. I arrived at the following: 123, 312, and 231 are even permutations and 213, 321, 132 are odd; thus, we should have Alt f(v1, v2, v3) = f(v1 + v3 + v2 - v2 - v3 - v1, v2 + v1 + v3 -...etc = f(0, 0, 0) = 0. Clearly, this isn't acurate since the wedge of a 3-linear f and a constant c should be cf, which isn't 0. What did I screw up? Thanks for any help:) 67.165.56.56 (talk) 16:10, 18 February 2010 (UTC)

It was indeed a stupid error, for whatever reason I was assuming f(a,b,c) + f(x,y,z) = f(a+x,b+y,c+z)...obviously not the case...:) 67.165.56.56 (talk) 16:32, 18 February 2010 (UTC)

February 19

No questions were asked today

February 20

Sinusoidal function of time

Its well known that if a sinusoidal function of time is squared (multiplied by itself), there will be produced a sinusoidal function at twice the original frequency. My question is: what if you try to take the square root of a sine function assuming that its instantaneous value never becomes negative? And does the answer depend upon the zero frequency offset (ie the constant) added to the sine function. Will the result be half of the original frequency? This is my personal interest and is not homework of any sort. —Preceding unsigned comment added by 79.76.244.151 (talk) 01:32, 20 February 2010 (UTC)

You can give it a try on a graphing calculator, such as [this online one]. Successively graph sin(x), 1 + sin(x) and sqrt(1 + sin(x)), then starting fresh, successive graph sin(x), abs(sin(x)), and sqrt(abs(sin(x))), and finally consider sin(x), (sin(x))^2 and sqrt((sin(x))^2). Don't just look at the results, but work through what is happening in your mind so that you could make a sketch graph of the functions without a calculator. You may then understand that the frequency is not so much due to the power (squared, square root, etc.) of the sine function as it is of how the function which originally yielded both positive and negative values was modified to yield only positive ones. (Your question was an excellent one, reflecting an inquisitive nature. Math should be explored, not just learned.) 58.147.58.28 (talk) —Preceding undated comment added 02:10, 20 February 2010 (UTC).

Also, note that sqrt(1 + sin(x)) is equal to sqrt(2) * abs( sin(0.5 * x + pi/4) ). So taking the square root of a sine function that was lifted up to just above x-axis does give the absolute value of a sinusoidal function with half the frequency. The trouble is that the sqrt function always returns the principal square root -- the positive one. If it somehow knew to return the negative value half the time then you would the function you originally asked about. So I suppose that the answer to your original question is "sort of".58.147.58.28 (talk) 06:11, 20 February 2010 (UTC)

The original poster wrote:

Its well known that if a sinusoidal function of time is squared (multiplied by itself), there will be produced a sinusoidal function at twice the original frequency.

But that's not true. It's true if the mean value of the original sine function is zero. But it's not true more generally. Try graphing this:

$y=\left(1+{\frac {3}{4}}\sin x\right)^{2}$

The frequency is only that of the original function, and the shape differs visibly from a sinusoid. Michael Hardy (talk) 04:23, 20 February 2010 (UTC)

Yes I forgot to put that condition in my original statement. Sorry! —Preceding unsigned comment added by 79.76.244.151 (talk) 10:52, 20 February 2010 (UTC)

Pi

Why most of the programmers use 4*atan(1)as a value of pi instead of 3.14159..... ? Does not the former way takes a long calculation time? —Preceding unsigned comment added by Amrahs (talk • contribs) 03:18, 20 February 2010 (UTC)

It is possible that an optimizing compiler can recognize that 4*atan(1) is constant and replace it with the appropriate constant value at compile time, so that there is no effect on the run time. Also, it is easier to remember 4*atan(1) than to remember π to the necessary number of decimal places (and it is less error-prone). Finally, the specifications for the atan function probably guarantee that the returned value will be as precise as possible given the target computer's representation of real numbers. —Bkell (talk) 04:41, 20 February 2010 (UTC)

INot sure why and havent seen it much but it may have to do with the intel floating point implementation which internally has 80 bits but if you specified pi directly would only be 64 bits. If you use the expression and it doesn't truncate the value it will be using a higher precision value in its calculation. Actually the IEEE 754-2008 specification also lists functions with pi factors in so they would also give higher accuracy if they were used. Dmcq (talk) 13:25, 20 February 2010 (UTC)

Are there many situations where you would need more than 64 bits of pi? --Tango (talk) 13:59, 20 February 2010 (UTC)

I think Dmcq is right, why not start with 80 digits when you can do it just as easily. But the x87 already has a load pi instruction built in so I'm not sure why you'd use atan instead.--RDBury (talk) 17:59, 20 February 2010 (UTC)oogle I found [http://www.derekroconnor.net/Software/Ng--ArgReduction.pdf

I just had a look up about this and the chip hoilds 66 significant bits plus the exponent. On google I got this Argument Reduction for Huge Arguments as my first reponse for'argument reduction sin'. They talk about needing 1144 significant bits! Dmcq (talk) 20:54, 20 February 2010 (UTC)

Unless the whole calculation, up to the point of comparing it with something, is done in registers, the extra precision will be lost when it gets rounded for writing to a 64-bit location in memory. Paul Stansifer 03:17, 22 February 2010 (UTC)

An arctangent calculation takes on the order of 100 machine cycles on a modern x86 with floating point hardware, i.e. usually less than 1/10th of a microsecond. That adds up if you do it a lot of times in some inner loop of a program, but for initializing a static value where you only do it once when the program starts, it's insignificant. On (say) an embedded ARM processor with no hardware floating point, the initialization would be a lot slower (several microseconds even) but still probably less significant than the possible code bloat of bringing in an arctangent routine that's not being used anywhere else. It is of course best if the compiler recognizes the arctangent function and precomputes it (partial evaluation) but if you're developing in a context where this is an issue, you should check the generated assembly code to make sure the compiler is doing what you hope. 75.62.109.146 (talk) 23:15, 20 February 2010 (UTC)

This is the Mathematics desk, but if you don't mind, and since you did use the word "programmers" in the question, I'll give more of a Computing-desk answer.

The answer does have as much to do with programming style and Software Engineering as it does with mathematics. Consider these four expressions:

1. float pi = 3.14;
2. float pi = 3.141592653589763238462;
3. float pi = 3.14159265358979323846264338327950288;
4. float pi = 4*atan(1);

Now, the first line has an obvious bug. It doesn't have enough significant digits; it will yield pretty significantly wrong answers in subsequent calculations. The second line, on the other hand, has a very non-obvious bug, one that might never be noticed. The third line is probably fine, for any reasonable application, but it might be a nuisance to type (if, for example, you didn't have Wikipedia's pi article handy, or if you were unclear on the copy of cut and paste); the third line is also a nuisance for anyone else to verify. The fourth line, however, is (with one exception) perfect: it is guaranteed to give you a value of pi which is exactly right, out to the numerical limit of whatever processor your code happens to be running on. The code is easy for you to type, and equally easy for your successor to verify. The only possible objection is efficiency, but if you're computing it just once and then assigning it to a variable (as in my example), or if you're a practitioner of "make it right before you make it fast", you can pretty easily see your way clear to going ahead and writing it that way, and changing it only if the efficiency problem is found to be significant. —Steve Summit (talk) 02:59, 23 February 2010 (UTC)

I've found the reason out, it's horrible. The constant M_PI has been in most math.h include files in C since year zero but it has not been included in some of the standards. I haven't worked out why yet and it seems really silly to me, the computing desk might know. You will be able to include it if you set some compiler switch or include something in the source but it won't be standard. Using 4*atan(1) conforms tot he standard. With a good compiler it won't be too bad because it'll evaluate it at compile time but that might only happen with a high level of optimization. Dmcq (talk) 09:55, 23 February 2010 (UTC)

4 * atan(1) has two problems that I see. One is performance: even a highly optimising compiler may not eliminate the calculation at compile time if atan() is provided by a library linked in at link time. Some compilers have switches to enable compile time elimination of math library functions, but not all compilers and not all functions. It's not part of the C or C++ standard so varies between implementations, and is something you need to check on each platform you're targeting.

The other problem might be accuracy. If you have e.g. "doubles are always floats" set, a performance option on most compilers, then all maths calculations are done with floats and so only 23 bits of accuracy. Every calculation done will introduce inaccuracies, including the above one. So 4 * atan(1) will probably be less accurate than typing out the digits.

So this is what I've always done, if someone hasn't already done it in the code I'm working on: define a constant (#define in C, const in C++) equal to 3.14159265358979323846, i.e. with more than enough digits (which I learned a long time ago) that it's accurate for whatever degree of accuracy is needed.--JohnBlackburne^words_deeds 12:16, 23 February 2010 (UTC)

Well, you could always put const double pi=4*atan(1); at file scope. Maybe it wouldn't evaluate it at compile time, but at the very least it should evaluate it only once per execution of the program. (For anyone worried about globals, my opinion is that global variables are a problem, global constants are not. --Trovatore (talk) 19:32, 23 February 2010 (UTC)

Composite number

Resolved

Okay, my name is NumberTheorist, but think of the restriction "in training". In fact, the best I had was an independent study in number theory as an undergrad and I didn't do a whole lot. But, I really want to learn this stuff. I'm just going through some problems from William Chen's lecture notes and I am not sure what to do on this one.

Show $n^{4}+4$ is composite for all $n>1$. I have figured out if $n\not \equiv 0\mod 5$, then it's easy as $n^{4}\equiv 1$ so that $5\mid n^{4}+4$. And, clearly if $n$ is even, the expression is composite. But, if $n$ is an odd multiple of 5, I don't know where to go. If you consider the first few, $n=5$ gives 629 = 17 * 37, $n=15$ gives 50629 = 197 * 257, $n=25$ gives 390629 = 577 * 677 so there is no small number that goes into these guys necessarily. Any ideas? This is only problem 3 in Chapter 1 of William Chen's "Elementary Number Theory" so it shouldn't be that hard. NumberTheorist (talk) 14:32, 20 February 2010 (UTC)

$n^{4}+4=(n^{2}-2n+2)(n^{2}+2n+2)$ Gandalf61 (talk) 14:29, 20 February 2010 (UTC)

Yea, I just figured that out :) Thanks for your help though. NumberTheorist (talk) 14:32, 20 February 2010 (UTC)

Getting to the South Pole

Assume that the earth is a perfect sphere. It is intuitively obvious that if one starts on the equator and maintains a constant bearing with a southwards component, one will eventually reach an arbitrarily small distance from the South Pole. If the bearing is 0.1° south of west, say, there will be a spiral path with many "circuits" of the southern hemisphere. For a bearing of 0.1° west of south, I've difficulty in visualising the path but think that it won't go too far from the line of original longitude - but will it again spiral round the pole, this time starting much closer to it? Is it possible to derive an explicit function of longitude in terms of latitude for a path of constant bearing? 81.131.164.207 (talk) 16:12, 20 February 2010 (UTC)

Yes, it will spiral round the pole. Since the bearing is closer to south than north, each step you take will take you closer to the pole, but since you aren't travelling due south you will never actually get to the pole. That results in a spiral. Of course, in real life you would eventually get closer to the pole than can be meaningfully distinguished from being at the pole. The best way to find the function would be to use something like the Mercator projection where Rhumb lines (which the line you are talking about is) are straight lines. The formula for a straight line is easy, so you just need to compose it with the projection and its inverse (see the projection's article for those formulae). --Tango (talk) 16:24, 20 February 2010 (UTC)

It's not the case that you never get to the south pole. The rate at which your latitude changes is constant and so the path length is finite. Rckrone (talk) 17:14, 20 February 2010 (UTC)

The rate at which your latitude changes as a function of time is constant, but not as a function of longitude, which is what we are talking about. If the path is finite in space, then what longitude would you have just before you reach the south pole? The time taken to reach the south pole is finite, so to say you never get there isn't really accurate (since "never" usually refers to time), you are right, but the path is not finite - the south pole is some kind of singularity. --Tango (talk) 17:30, 20 February 2010 (UTC)

Well, that's not right either... the length is finite, but the path doesn't have an end-point. My use of language leaves something to be desired... --Tango (talk) 17:33, 20 February 2010 (UTC)

Another way of representing the path might be as a logarithmic spiral round the south pole on a stereographic projection round there. Dmcq (talk) 17:57, 20 February 2010 (UTC)

You would wind infinitely many times around the pole, but the length of the path to the pole is still finite. Michael Hardy (talk) 18:09, 20 February 2010 (UTC)

(please WP:INDENT; this is a response to the OP) From a basic differential equation treatment, I get that ${\frac {d\phi }{d\theta }}={\frac {\tan a}{\sin \theta }}$, where θ is colatitude (π at the south pole), φ is longitude, and a is your angle east of south. We can directly integrate this to get $\phi (\theta )=\phi _{0}-\tan a\,\ln(\csc \theta +\cot \theta )$. This is of course equivalent to the statements in the articles Tango mentioned, but I thought this different approach interesting. --Tardis (talk) 18:36, 20 February 2010 (UTC)

Thanks to all. 81.131.164.207 (talk) 19:30, 20 February 2010 (UTC)

Complex Radius of Convergence

Hi all.

On the 'radius of convergence' page, it says that "The radius of convergence of a power series f centered on a point a is equal to the distance from a to the nearest point where f cannot be defined in a way that makes it holomorphic". Can anyone direct me to a proof of that? Now with say, tan(z) for example, obviously the function is well-behaved until we hit pi/2, but how do we show that f 'can't be defined to make it holomorphic'? I think the very concept of this confuses me - surely the function is defined erm... by its definition. Is this the same as saying we just can't define any power series which agrees with f on every point of radius R from a? How can it 'agree with f' anyway if that is the case - surely if we can't define f as a power series, then how can we define it in cases like tan(z), etc? In that case, how do we show that? Perhaps if I saw a proof of whatever theorem they're referring to then things would be clearer - any insight would be great - thanks very much.

Estrenostre (talk) 18:34, 20 February 2010 (UTC)

See holomorphic functions are analytic. The fact being proved there is different but the same method of proof is applicable to your question. Also see Lars Ahlfors' book on the topic (or any of a few dozen others.... Michael Hardy (talk) 21:47, 20 February 2010 (UTC)

...as for your other questions (besides where to find a proof): One cannot extend the tangent function by defining its value to be some particular complex number at π/2 in such a way that the new function extending the tangent function is holomorphic at that point (nor even continuous, in this case). Michael Hardy (talk) 21:51, 20 February 2010 (UTC)

Yes. I would like to add that just because tan has a power series around 0 doesn't mean the value of that series agree with tan everywhere; its only valid in the maximal open disc containing 0 at which tan is differentiable. Money is tight (talk) 21:53, 20 February 2010 (UTC)

For your question of how do we define tan; first define the exponential function exp(z) as the standard power series, then define sin(z)=(exp(iz)-exp(-iz))/2i, cos(z)=(exp(iz)+exp(-iz))/2, tan(z)=sin(z)/cos(z). Money is tight (talk) 21:58, 20 February 2010 (UTC)

Ah, that makes sense, the definition is much clearer in the article you suggested - thankyou! Estrenostre (talk) 21:12, 21 February 2010 (UTC)

Probability Question

Consider an urn with 6 red balls and 3 blue balls. There are three people (A,B,C) who will each draw one ball from the urn. What is the probability of drawing a blue ball for each individual?

My thought is that each one has the same probability regardless of order, and my calculations seem to show this to be true. However, I have trouble explaining why this is the case. I know this seems like a homework question, but it actually has to do with simplification of a computer algorithm. 199.111.191.177 (talk) 19:51, 20 February 2010 (UTC)

If they draw with replacement, you just cube the probability of one of them doing it (because they're independent). If they draw without replacement, the order still doesn't matter (they are exchangeable events), but they're not independent, so you have to handle it differently. Here it's just that one of the many ways to pick 3 objects from 9 is a success, and all the others are failure. Either way, this experiment is a simple random sample. --Tardis (talk) 20:15, 20 February 2010 (UTC)

To convince yourself, you may wish to consider the conditional probabilities. P(B draws red) = P(A draws red) * P(B draws red given A draws red) + P(A draws blue) * P(B draws red given A draws blue). Knowing what A drew tells you how may balls of each color are available for B to draw from. 58.147.58.28 (talk) 20:57, 20 February 2010 (UTC)

Thanks for the links. However, I seem to have found something even more puzzling. Let's return to the original example and instead of using the given urn, we used a basket containing 8 red balls and 1 blue ball. If each of three people (A,B,C) draw one ball (without replacement) from the basket, it seems to be intuitively true that whoever draws first has a higher chance of drawing the blue ball. Yet, when computing the probabilities, they all worked out to be the same once again! Assuming, A draws first, his chances are obviously (1/9). Then, if B draws second, B's chances are (8/9)*(1/8)=(1/9). Lastly, C's chances are (8/9)(7/8)(1/7)=(1/9). I have come to understand this to mean that even though B will only have a chance 8 out of 9 times of drawing the blue ball, his overall chance is the same due to his improved odds due to the presence of one less red ball in each of those 8 times. This is also similarly true for C.

I tried one last case, which is the same as the last example with the exception that the first two people get to draw four times without replacement. After going through the calculations, A has a (4/9) chance, B has a (4/9) chance and C has a (1/9) chance. I think I am beginning to understand this. 199.111.191.177 (talk) 23:06, 20 February 2010 (UTC)

I don't think the intuition is valid. Say you write a number on each ball, so the blue ball is #5 and the other numbers are on red balls. Then you permute the balls at random. The blue ball will end up in position 1, 2, 3, etc. with equal probability. The drawing-without-replacement process just means permuting the balls, then giving the ball in position 1 to A, the ball in position 2 to B, and the ball in position 3 to C. Each has equal probability of getting the blue ball. 75.62.109.146 (talk) 23:23, 20 February 2010 (UTC)

I have come to understand this to mean that even though B will only have a chance 8 out of 9 times of drawing the blue ball, his overall chance is the same due to his improved odds due to the presence of one less red ball in each of those 8 times. Right! I would think that it would be intuitive that A's draw has a certain probability of increasing B's chances and a certain probability of decreasing (in this case ruining) B's chances. What might not be intuitive is that when you do the calculations the fractions work their way to give equal probabilities for all three players. I would think that the general presence (or lack) of an intuitive sense of equal probabilities here is important to the tradition of drawing lots. We do not read of Jonas first drawing lots to determine the order of drawing lots. Psychologically, the impact of going last could depend on whether the drawn lots are concealed until all have been drawn. I'd hate to be the sixth man and receive the revolver in a game of Russian roulette where the cylinder is not spun between tries. It only had a 1/6 chance of occurring, but I know what is going to happen when I pull the trigger. 58.147.58.28 (talk) 03:07, 21 February 2010 (UTC)

I was just thinking that some of the same issues of intuition are involved in the Monty Hall problem. I am convinced that the majority of its controversy was due to the ill defined problem where it is not explicitly stated that the host intentionally chooses a goat to draw out the tension of the contest. (The mathematicians who wrote in objecting to vos Savant's answer assumed that the door which happened to reveal a goat was chosen at random, as most such problems which are presented in the study of probability explicitly state the bias where it exists. The revealed door chosen on the game show is almost certainly not chosen at random, but it is possible that the show is running over budget that week, and the host will intentionally open the door with the car if the contestant had not initially chosen correctly. In that case a goat is only revealed to attempt to lead the contestant away from the prize, and the best strategy is to stand pat.) I am shocked that our Monty Hall problem article (a featured article, nonetheless) says in its lead Some critics pointed out that the Parade version of the problem leaves certain aspects of the host's behavior unstated, for example, whether the host must open a door and must make the offer to switch. However, such possible behaviors had little or nothing to do with the controversy that arose, and the intended behavior was clearly implied by the author. That may be verifiable, but it is patently false. (It would be better to concentrate on the motivation of the host's choice in choosing which door to reveal, that is, whether it was a random choice or not.) 58.147.58.28 (talk) 03:35, 21 February 2010 (UTC) I'd be thrilled to win a goat. I love goats!

Exhaust sound

 Hello

I've been dealing with honda bike for more than 2 decades

I'm currently designing sports bike as a result.

One of the huge challenges I'm facing, is about exhaust sound.

I need help.

I look forward to your response

IBRAHIM ABDOULLAHI from Cameroon —Preceding unsigned comment added by 195.24.193.34 (talk) 20:13, 20 February 2010 (UTC)

Well you'll already know more than anybody here I'd guess but have you seen the muffler article. I'd have though nowadays one could do active noise cancellation as well. Dmcq (talk) 21:08, 20 February 2010 (UTC)

February 21

How to find the domain and range of this function?

A function f(x) has domain {x e R | x ≥ -4} and range {y e R | y < -1}. Determine the domain and range of this function:

y = -2f ( -x + 5 ) + 1

Apparently, the answer is

domain {x e R | x ≤ 9}, range { y e R | y > 3}

but I'm not sure how to arrive at this answer. I don't even know where to begin! If anyone could help, I would greatly appreciate it. Could someone tell me what steps would be necessary to get to the answer? -- —Preceding unsigned comment added by 74.12.20.185 (talk) 04:46, 21 February 2010 (UTC)

Perhaps the confusion comes from the use of x and y in two separate equations. (This is perfectly valid, but it can been disorienting.) Let's restate the second half of the problem as:

Define the function g(t) = -2f(-t+5) + 1. What are the domain and range of g(t)?

The domain of g(t) are the permissible values for t. You know the domain of f(x), so you know the permissible values for the argument of the function f, and in this case the argument is -t + 5. So, what values can t be if -t + 5 ≥ -4? The range of g(t) are the possible values that the function can obtain. You know the range of the function f(x), which is the same as the range of f(-x + 5) [Does that make sense? It is still just the function f.] so what values can -2f(-x + 5) + 1 obtain if f(-x + 5) < -1?

Relevant articles are range, domain, function composition, inequalities. 58.147.58.28 (talk) 05:16, 21 February 2010 (UTC)

Integration

Suppose we wanted to calculate the work done in going around a small rectange in the xy plane with dimensions Δx and Δy, with (Δx,Δy)-->0 (the two top sides are parallel to the x-axis). So we start by looking at the work done in travelling through the paths parallel to the x-axis. This is equal to $\int _{x,y}^{x+\Delta x,y}\!F_{x}(x,y)\,dx$ + $\int _{x+\Delta x,y+\Delta y}^{x,y+\Delta y}\!F_{x}(x,y)\,dx.$ Because Δx is said to be small, F_x is assumed to be roughly constant over the interval x to x+Δx. Thus, we get W=F_x(x,y)Δx - F_x(x,y+Δy)Δx, which we say is NOT equal to zero. Thus, the we are allowing for the fact that y is different between the two paths but are ignoring the variation of x along each of the paths. In other words, we are saying that the variation of F_x isn't significant in comparison to Δy. Why would this be true? 173.179.59.66 (talk) 05:34, 21 February 2010 (UTC)

Basically it's like using just the first term of a Taylor series, which is ok when the interval is small. Suppose you want to include a second-order correction: you end up with terms like $F_{xx}(\Delta x)^{2}$ and so forth, where since $\Delta x$ is so small, its square is swamped out by the first-order term. Try writing it out that way and seeing what the limit looks like as $\Delta x$ and $\Delta y$ approach zero. 75.62.109.146 (talk) 07:01, 21 February 2010 (UTC)

Hmm, I seem to be having trouble seeing how to write the integral as a Taylor series. Can you please show me? Thanks! —Preceding unsigned comment added by 173.179.59.66 (talk) 08:08, 21 February 2010 (UTC)

I don't mean literally write a Taylor series, I just mean it's the same idea. The Taylor series says f(x+h)=f(x)+hf'(x)+(h²/2)f''(x)+... . The integral you showed is a first-order approximation, so try writing out a few of the second-order correction terms and seeing what they look like. The point is that when h is small, h² is very small. 75.62.109.146 (talk) 21:41, 21 February 2010 (UTC)

You can though. $\int _{x,y}^{x+\Delta x,y}\!F_{x}(x,y)\,dx$ = F(x+Δx,y) - F(x,y). The Taylor expansion of F(x+Δx,y) is F + ΔxF_x + Δx²F_xx/2! +..., so we get F(x+Δx,y) - F(x,y) = ΔxF_x + Δx²F_xx/2! +...

For the second integral we get F(x,y+Δy) - F(x+Δx,y+Δy) = -ΔxF_x(x,y+Δy) - Δx²F_xx(x,y+Δy)/2! -...

The sum of those two is Δx(F_x(x,y) - F_x(x,y+Δy)) + Δx²(F_xx(x,y) - F_xx(x,y+Δy))/2! +...

Then we use a Taylor series over y to get -Δx(ΔyF_xy + Δy²F_xyy/2! +...) - Δx²(ΔyF_xxy + Δy²F_xxyy/2! +...)/2! -...

All the subsequent terms are dominated by -ΔxΔyF_xy as Δx and Δy get small. Treating F_x as constant over the x interval is equivalent to ignoring the terms with Δx², which is good. But treating F_x as constant over the y interval is equivalent to ignoring the terms with Δy, which is bad because that's everything. Rckrone (talk) 22:30, 21 February 2010 (UTC)

Schlafli symbol

Should the Schlafli symbol {6/2} be interpreted as a polygon compound or as a doubly-wound triangle? 4 T C 07:03, 21 February 2010 (UTC)

It's a hexagram. That Schlafli symbol tells you to take 6 evenly spaced vertices and connect every second one. Rckrone (talk) 07:27, 21 February 2010 (UTC)

are there any free & meritorious statistics lessons/courses to be found online?

Through various quirks of scheduling, a bit of self-study, and odd luck I managed to complete a BS in Geology and an MS in Environmental Policy without ever once taking a course in statistics, not even in high school. At this point in my life it is a source of inward embarrassment and occasionally a professional impediment. As such, I'd like to fill this gap in my knowledge on my own time. I would be grateful if someone could point me towards a reputable online source for statistics instruction from basically scratch? 218.25.32.210 (talk) 08:29, 21 February 2010 (UTC)

http://ocw.mit.edu/OcwWeb/Mathematics/index.htm seems to have some. 75.62.109.146 (talk) 21:38, 21 February 2010 (UTC)

name of method for generating a circular path in x, y plane

Hi!
Does anyone know the name for the method of generating a circular path using the two equations
(1) x += y / R
(2) y -= x / R ?

I remember reading about this years ago in wikipedia and now the name of the method escapes me.
It's got to be something simple, but looking under the list of List_of_numerical_analysis_topics I can't find it again... It's based on starting from a known point (x, y) anywhere on the circle of radius R, and moving to another spot on the circle by adding a velocity vector V = ( y/R, -x/R). Actually, the velocity vector V's magnitude |V| can be any fractional component. It's a nifty way to generate sine and cosine values.

Just to clarify, R is the radius of the circle plotted. Fex, a circle of radius R = 10 would go like this...

Step	x	y
0	10	0
1	10	-0.1
2	9.9	-1.09

Thanks! --InverseSubstance (talk) 22:45, 21 February 2010 (UTC)

CORDIC Dmcq (talk) 23:22, 21 February 2010 (UTC)

You might also be interested in Midpoint circle algorithm if doing circles Dmcq (talk) 23:26, 21 February 2010 (UTC)

February 22

Modal logic

From the article, just trying to understand the semantics.

We have a non-empty set (frame) $G$, and $v,w\in G$ are worlds. We have a accessibility relation $R$, such that $vRw$ means that $v$ is possible in $w$.

As an example:

$p$ = it is snowing

$w$ is $\Box p$. $v$ is $\Diamond p$.

Therefore $vRw$.

Does this mean $R$ is like an equality relation, or a kind of "is a subset of" relation? —Preceding unsigned comment added by 81.149.255.225 (talk) 10:29, 22 February 2010 (UTC)

It does not make sense to say that "v is possible in w". You can ask whether a statement (formula) is possible in a world, but there is no concept of a world being possible in another world. The intuitive meaning of the accessibility relation v R w is actually that every statement that is true in w is possible in v. However, it's not really defined like that, it's a primitive notion: you are given a set of worlds, an accessibility relation, and truth values of atomic statements in each world, and all this together determines the truth values of compound statements (which may involve the $\Box$ and $\Diamond$ operators), see Kripke semantics. Your example does not make much sense as is, but even if we read it as "$\Box p$ is true in w and $\Diamond p$ is true in v", this is insufficient information to determine whether v R w or not. The accessibility relation can be an arbitrary binary relation, in general it does not have to be transitive or reflexive, hence neither equality nor "subset of" is an adequate analogy.—Emil J. 14:52, 22 February 2010 (UTC)

The double turnstile ⊨ is read 'models' rather than 'is', where models here means the right hand side proposition is true for the world given by the left hand side. p is a proposition and w is a world. I think your business about inclusion is where you are thinking of R as implementing the most common system, what the article calls the strongest logic S5, but this isn't necessarily so. Dmcq (talk) 15:16, 22 February 2010 (UTC)

What more do we need to know in order to Identify a function

If we know f(n)=(1/n^2) for all integers n, and f is analytic in the complex plane except for possibly at some singularities, then what more would we need to know in order to establish g exactly? Obviously you could have g(z)=cos(2piz)/(z^2) or something similar so it needn't necessarily be g(z)=1/z^2 at this point - but I can't see how we can classify all possible g which take the appropriate values at integers, in order to work out what more information we need to know to identify g. Could anyone suggest anything?

Thanks all very much! 82.6.96.22 (talk) 13:34, 22 February 2010 (UTC)

Your condition on g is equivalent to g(z) = 1/z² + h(z), where h is a function meromorphic in C (assuming that's what you mean by "analytic except for possibly at some singularities") which vanishes in all integer points. You can thus ignore the 1/z² part, and concentrate on the (less messy, if not really easier) task of classifying such h.—Emil J. 14:59, 22 February 2010 (UTC)

Centre of a group algebra

Why do the conjugacy class sums of a group, G, form a basis of the center of the group algebra, FG, for some field F? I've tried it out for a few concrete examples, and it worked, but I can't really see why. The closest I could come was taking h to be in the centre - then hz = zh for all z in the algebra, so $h=z^{-1}hz$, which introduces conjugation, but that's only true when z has an inverse in the algebra. I know also that the class sums are invariant under conjugation by the elements of G (i.e. the basis elements of FG), but I can't seem to string it altogether. The notes I'm working with only dedicate one line to the explanation, so I feel I'm missing something pretty obvious. Thanks, as always! Icthyos (talk) 18:02, 22 February 2010 (UTC)

I think you're over thinking the problem. Let z be in the center of the group algebra and write

$z=\sum z_{g}g$

Then

$z^{h}=\sum z_{g}g^{h}=\sum z_{g^{h^{-1}}}g$

where the second sum is obtained by reindexing the first one. But z=z^h for all h so matching coefficients

$z_{g}=z_{g^{h^{-1}}}$

for all h. In other words the value of z_g depends only on the conjugacy class of g. So z can be written

$z=\sum z_{C}C$

where the sum runs over the conjugacy classes C of the group. The Cs are obviously linearly independent and they are in the center, so they form a basis. The proof is kind of obvious if you've been working with these sums long enough, but probably not if you never seen them before. My group theory book (W.R. Scott) gives the proof in 7 lines, slightly different than the one here.

A-hah, I see now - thanks for the help. Icthyos (talk) 21:37, 22 February 2010 (UTC)

Math Help

Yes- I realize you won't help me with my homework, but I have no idea where to start here.

Can someone give me the equations?

Arriana bought two kinds of stamps, 50cent stamps, and 65cent stamps. She bought 40% more 50cent stamps then 65 cent stamps, spending a total of $50.56. How many of each type did she buy? There is a 7% tax on stamp sales.

Thanks in advance. —Preceding unsigned comment added by 174.112.38.185 (talk) 21:55, 22 February 2010 (UTC)

Start by giving a name to everything you dont know. these are called variable for some reason

x for the number of 50c stamps

y for the number of 65c stamps

and then write them in like 40% more 50c stamps means take y and 40% of y and you get x or shorter

(1 + 40/100)y = x

All you do is write down the x ory instead of the actual amounts in each of the other statements as well and you've got some equations. Dmcq (talk) 22:07, 22 February 2010 (UTC)

(ec)Variables are useful here. When you want to manipulate some number, but you don't know what the number is, place a variable in its stead; this gives you information about the variable which later may allow you to determine its value.

Let x be the number of 65 cent stamps that she bought. Then answer the following questions in terms of x. How much did the 65 cents stamps she purchased cost? How many 50 cent stamps did she purchase? How much did they cost? What is the total cost (before tax) of all the stamps she purchased? How much did she spend (after tax)?

You know that the answer to the last question is $50.56 from the problem statement. Once you've answered the last question in terms of x (using your previous answers), you will have an equation for x. This will allow you to calculate x and solve the problem from there. Eric. 131.215.159.171 (talk) 22:11, 22 February 2010 (UTC)

Everyone acts as if mathematics is the only way to solve these problems, when sometimes the humanities will suffice. (I suppose that's what you get when you ask such a question in a mathematics forum. When your only tool is a hammer, ...) In this case a little detective work will do. I followed Arriana to the post office when she mailed off her wedding invitations, and she crossed a name off her list as she put a stamp on each envelope. I pulled that list out of the trash after she left and found out that the total number of guests receiving invitations happens to be the same as the lim sup of the largest finite subgroup of the mapping class group of a genus $g$ surface divided by $g$. More over, the number of guests who lived locally, and not over the border in Canada (and thus requiring the higher international postage), was the square of the largest prime factor of the total number of guests. 58.147.60.130 (talk) 01:50, 23 February 2010 (UTC)

Indeed I must admit I was wondering why they couldn't just ask Arriana or look at the stamps, and why did they want to know anyway? Surely you'd only want to know how any stamps you've got left. Dmcq (talk) 12:00, 23 February 2010 (UTC)

February 23

98765321 / 1233456789

98765321 / 1233456789 —Preceding unsigned comment added by 71.143.224.27 (talk) 05:08, 23 February 2010 (UTC)

What is your question? Any calculator will give you a value of about 0.8. Are you wondering why there are two 3's in the denominator? Are you wondering what / means? Are you wondering why your computer didn't instamagically speak the answer to you when you randomly typed numbers into some random website that you stumbled upon? -- kainaw™ 05:17, 23 February 2010 (UTC)

Perhaps it was a typo and the OP meant to ask about the progress of the sequence 1₂/1₂, 21₃/12₃, 321₄/123₄, 4321₅/1234₅, ..., specifically the fact that $\lim _{b\to \infty }{\frac {1}{b-2}}{\frac {\sum _{n=1}^{b}nb^{n-1}}{\sum _{n=1}^{b}nb^{b-n}}}=1$. 58.147.60.130 (talk) 06:50, 23 February 2010 (UTC)

I thik they probably duplicated the 3 in the second number. Perhaps this is some sort of alien maze test on the reference desk to see how it scurries around when presented with random stuff? I've noticed mopre and more of these type questions where they just enter some random search query with random keywords as if querying google. I think the answer is they should enter it into google. Dmcq (talk) 12:07, 23 February 2010 (UTC)

One sometimes sees it mentioned that 123456789 × 8 = 987654312, just because the pattern in the digits is amusing. Michael Hardy (talk) 13:26, 23 February 2010 (UTC)

Problem 323 in The Moscow Puzzles by Boris A. Kordemsky presents the following four numbers, each of which is an arrangement of the ten digits 0 through 9:

2,438,195,760; 4,753,869,120; 3,785,942,160; 4,876,391,520.

Each of these numbers is divisible by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, and 18. —Bkell (talk) 22:52, 23 February 2010 (UTC)

Inversion in a Galois Field

Hello, for a computer science project, I am looking for an algorithm that will invert any given element (zero maps to zero) in the Galois Field GF(2^128) and give me its multiplicative inverse. The problem is that my background in abstract algebra/number theory is very limited (one undergrad course in each) so can anyone please point me to a good resource on the internet that I can use to write my own source code. Something fast and efficient preferably. If somebody has an m file laying around that already does this or if someone known how to do this on MATLAB for example, it would be appreciated. This is just one of the steps in a larger scheme. Oh and I also have an irreducible polynomial given as the modulus. Thanks! 174.29.98.151 (talk) 07:10, 23 February 2010 (UTC)

If you just want a straightforward implementation, use the extended Euclidean algorithm. If you want highly optimized code, web search on "finite field inversion". A huge amount of work has been done to optimize that operation, for elliptic curve cryptography and other reasons. 75.62.109.146 (talk) 07:22, 23 February 2010 (UTC)

Woah, that works for all finite fields? I thought it only worked for $\mathbb {Z} /n\mathbb {Z}$. 174.29.98.151 (talk) 07:29, 23 February 2010 (UTC)

How do you represent the finite field F = GF(p^d) with p prime? You fix an irreducible polynomial f(x) over $\mathbb {Z} /p\mathbb {Z}$ of degree d, you define F to consist of all polynomials of degree less than d, you add them as usual, and you multiply them modulo f. Computing an inverse in F then amounts to computing an inverse polynomial modulo f, and that's what the extended Euclidean algorithm (for polynomials in $(\mathbb {Z} /p\mathbb {Z} )[x]$, not for integers) does. In order to implement it, you have to do computations in $\mathbb {Z} /p\mathbb {Z}$, and in particular to compute inverses in $\mathbb {Z} /p\mathbb {Z}$ you'll also need the extended Euclidean algorithm, this time for integers. But these two are separate issues.—Emil J. 11:43, 23 February 2010 (UTC)

Bijection

Let's assume that our domain of discourse is the set of real numbers.

So, is Ln(X^2) a bijection between the set of positive numbers and the domain of discourse?

Let me explain my question:

On one hand, Ln(X^2) does seem to be a bijection between the set of positive numbers and the domain of discourse, because for every two positive numbers, a,b, if Ln(a^2)=Ln(b^2) then a=b.

On the other hand, Ln(X^2) does not seem to be a bijection between the set of positive numbers and the domain of discourse, because if Ln(k^2) is a number belonging to the domain of discourse, then k is unnecessarily a positive number!

I have a technical question about either option which will turn out to be true:

On one hand, if the first option is correct, and Ln(X^2) is really a bijection between the positive numbers and the domain of discourse, although when Ln(k^2) belongs to the domain of discourse then k is unnecessarily a positive number, then how should I briefly express the fact that: f(X) is a bijection between the set A and the domain of discourse, so that every k (belonging to the domain of discourse) is correspondent - by the inverse correspondence of f - to a single number, and this number belongs to A?

On the other hand, if the second option is correct, and Ln(X^2) is not a bijection between the set of positive numbers and the domain of discourse, because if Ln(k^2) is a number belonging to the domain of discourse then k is unnecessarily a positive number, then how sould I briefly express the fact that: f is a function, whose domain is A, and whose image is the domain of discourse (i.e. f is on the range), so that for every two numbers a,b belonging to A, if f(a)=f(b) then a=b?

HOOTmag (talk) 09:23, 23 February 2010 (UTC)

$\ln(x^{2})$ by itself is not a function. To define a function you need to specify its domain. Usually it is understood that the domain is implicitly specified to be the largest domain possible for the expression, but in your question this seems to be a source of confusion. The function $f:(0,+\infty )\to \mathbb {R} ,x\mapsto \ln(x^{2})$ is injective, while $g:\mathbb {R} \backslash \{0\}\to \mathbb {R} ,x\mapsto \ln(x^{2})$ is not. They are both surjective, and thus f is bijective. -- Meni Rosenfeld (talk) 09:47, 23 February 2010 (UTC)

By "bijection" I meant "one to one correspondence". I'm unnecessarily talking about a function, although every one to one function is also a one to one correspondence.

A correspondence, as well as a one to one correspondence, must have a domain of discourse. In our case, the domain of discourse is the set of real numbers.

My question is about how to interpret the phrase "one to one correspondence between A and B".

Does the phrase "one to one correspondence between A and B" mean that every a belonging to A may indeed be correspondent (by that correspondence) to many elements, of which one single element only - is in B, and that every b belonging to B may indeed be correspondent (by the inverse correspondence) to many elements, of which one single element only - is in A, or: does the phrase "one to one correspondence between A and B" mean that every a belonging to A is correspondent (by that correspondence) to one single element b only, and that b is in B, and that every b belonging to B is correspondent (by the inverse correspondence) to one single element a - only, and that a is in A?

The same question may be asked about a "one to one function between A and B": Does it mean that every b belonging to B is correspondent (by the inverse correspondence) to many elements, of which one single element only - is in A, or: does the phrase "one to one function between A and B" mean that every b belonging to B is correspondent (by the inverse correspondence) to one single element a - only, and that a is in A?

HOOTmag (talk) 12:25, 23 February 2010 (UTC)

Have you read Binary relation? The larger universe (or domain of discourse) has no impact on the characteristics (injective, surjective, bijective, etc.) of a correspondence or function. As Meni Rosenfeld stated above, a function is defined by its domain, its range, and a rule mapping between them; changing the domain or range can change characteristics of the function because it means defining a new function, even it that new function seems a natural extension of the old one. Likewise a correspondence between sets A and B does not depend on the larger universe. So when you speak of a correspondence between A and B it makes no sense to talk of a corresponding to b if a is not an element of A or if b is not an element of B. There may be what seems to you a natural extension of the correspondence to a larger universe, but that is immaterial for considerations of the correspondence itself. 58.147.60.130 (talk) 15:23, 23 February 2010 (UTC)

Also, when you write "correspondence", do you mean a "binary relation that is both left-total and right-total" as defined in Binary relation#Special types of binary relations? 58.147.60.130 (talk) 16:01, 23 February 2010 (UTC)

Note that you may define a function $f:\mathbb {Z} \to \mathbb {Z}$ by $x\mapsto x+1$, or $x\mapsto 1+x$, or $x\mapsto x\cos(2\pi x)+1$, and it is all the same function. Were you to expand the domain and range onto the reals, then using the first two rules would give you a bijection; using the third rule would not. This does not change the fact that $f$ with its original domain and range is bijective if defined by any of the the three rules, because with that original domain the rules are equivalent. 58.147.60.130 (talk) 16:01, 23 February 2010 (UTC)

Let's put it this way: F is a function, and A,B,C are sets. Is there a simple phrase expressing the following two pieces of information (at once)?

When the domain of F is taken to be A, and the codomain of F is taken to be B, then:

1. For every a,b belonging to the domain of F, if F(a)=F(b) then a=b.
2. The image of F is C.

Do you see now my problem? If I simply say that F is a surjective from A onto C (thus informing that C is the image of F), then I miss the first information (i.e. the information that when the domain of F is taken to be A, and the codomain of F is taken to be B, then: for every a,b belonging to the domain of F, if f(a)=f(b) then a=b). However, if I simply say that F is a bijection between A and C (or is an injection from A to B, or to C), then I miss the second information (i.e. the information that when the domain of F is taken to be A, and the codomain of F is taken to be B, then the image of F is C).

HOOTmag (talk) 17:35, 23 February 2010 (UTC)

I am trying, but no, I am not seeing your problem yet. For a function to be bijective is equivalent to it being both injective and surjective. So saying that $f:D\to B$ is a bijection satisfies both your 1. and your 2. What am I missing? If $f:D\to A$ and $B\subseteq A$, then saying that the image of $f$ is $B$ is equivalent to saying that $f$ with its codomain restricted to $B$ is surjective. (I doubt that this is the problem, but you do know, don't you, that a one-to-one function is another name for an injective function, but a one-to-one correspondence is another name for a bijective function.) 58.147.60.130 (talk) 18:05, 23 February 2010 (UTC)

You've replied to an old version of my question. I'd changed my question before you answered (but after you saw the old version). Please review my question again. Anyways, If I simply say that F is a bijection between A and C (or is an injection from A to B, or to C), then I miss the second information, i.e. the information that when the domain of F is taken to be A, and the codomain of F is taken to be B, then the image of F is C. HOOTmag (talk) 18:18, 23 February 2010 (UTC)

Do you agree that if f is a bijection (or even just a surjection) from A to C then then C is the image of any function f redefined by simply changing its codomain? (The codomain of a function is always a superset of its image.) If so, then doesn't saying that f is a bijection between A and C give your second statement? Likewise, if you take any function f from A to B and restrict the codomain of the function to the image, then that new function is surjective. Are we still chasing each other in circles here? Rereading you question 3 outdents above, yes, saying that f is a surjective function from A onto C gives you item 2. but does miss item 1. Saying that f is a bijection from A to C gives 1. (because bijection implies injection) but it also gives you 2. (because bijection implies surjection). (Note the comment in my previous reply about the ambiguities of one-to-one.)58.147.60.130 (talk) 18:48, 23 February 2010 (UTC)

I don't accept your first assumption, because changing the codomain may change the image. For example, when the domain is the set of positive numbers, and F(x) is defined to be the number whose absoloue value is x, then the image of F is the set of positive/negative numbers - when the codomain is the set of positive/negative numbers respectively. Hence, the image is dependent on the codomain (not only on the domain).

To sum up, if I simply say that F is a bijection between A and C (or is an injection from A to B, or to C), then I miss the information that when the domain of F is taken to be A, and the codomain of F is taken to be B, then the image of F is C.

HOOTmag (talk) 21:21, 23 February 2010 (UTC)

There is a slippery semantic slope (one that I may have already crossed) to beware of when speaking of redefining a function by changing its domain or codomain, because, as Meni Rosenfeld pointed out, they are integral to the definition of the function. (See Binary relation#Is a relation more than its graph?) When I spoke of redefining the codomain I was implying that both the "before" and "after" codomains were subsets of some larger codomain where we had still defined a function, but as you point out this need not be the case.

Consider your inverse absolute value binary relation on the reals so that x inv_abs y iff x = abs(y). This is not a function because 1. it is not left-total (there is no y so that -1 inv_abs y) and 2. it is not functional (2 inv_abs 2 and 2 inv_abs -2). If we restrict the domain to the positive reals (as you suggested) it becomes left-total. If we then restrict the codomain to either the positive reals or the negative reals it becomes functional and is in fact a bijection. 58.147.60.130 (talk) 02:25, 24 February 2010 (UTC)

(←)So I believe that I do get a sense of where your unease originates, but I think that with precise language no contradiction appears. I have reread this section, and I believe that all your questions, as stated, are properly answered "bijection". So can you precisely restate your problem with a well defined function or relation? I suggest that for clarity we stick with terms such a function, relation, domain, codomain, injection, surjection, and bijection, avoiding the terms correspondence, range, one-to-one, and domain of discourse unless we specifically define them here. (I have been guilty of using range as a synonym for codomain instead of image -- a minority usage that I will eschew.) 58.147.60.130 (talk) 02:25, 24 February 2010 (UTC)

It seems what HOOTmag has in mind is not a function or a relation, but rather a formula. For example, the formula $\varphi (x,y)=(|y|=x)$. Given a domain A and codomain B, the formula induces a relation $\{(x,y)|x\in A,y\in B,\varphi (x,y)\}$. The question is about the property of $\varphi$, "The relation induced by $\varphi$ from A to B is bijective from A to C". This looks like a short way to describe it, but any shorter one will depend on a convention for denoting the induced relation, of which I am not aware. -- Meni Rosenfeld (talk) 08:30, 24 February 2010 (UTC)

Exponential function

I have seen e defined as limit of (1-1/n)^n as n-->∞, but from this definition how one arrive at the equation e^x=lim(1+x/n)^n as n-->∞. I've googled it, but couldn't find a proof anywhere. —Preceding unsigned comment added by 173.179.59.66 (talk) 12:10, 23 February 2010 (UTC)

One way of seeing it is:

$e^{x}=[\lim _{n\to \infty }(1+{\frac {1}{n}})^{n}]^{x}$

$=\lim _{n\to \infty }[(1+{\frac {1}{n}})^{n}]^{x}$

$=\lim _{n\to \infty }(1+{\frac {1}{n}})^{nx}$

$=\lim _{n\to \infty }(1+{\frac {x}{nx}})^{nx}$

$=\lim _{m\to \infty }(1+{\frac {x}{m}})^{m}$

Where the last step is substituting m = nx. The first step can be justified by continuity of exponentiation, and the last step is only justified if we recognize that the limit is taken over the entire real numbers, as opposed to just over the integers. --COVIZAPIBETEFOKY (talk) 13:07, 23 February 2010 (UTC)

Two books you might look at are

• Walter Rudin's Principles of Mathematical Analysis;
• Leonhard Euler's Introductio in Analysin Infinitorum.

Note that it's

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

with "+" rather than "−".

Also, you can make "COVIZAPIBETEFOKY"'s TeX display look better by doing it like this:

${\begin{aligned}e^{x}&=\left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]^{x}\\[6pt]&=\lim _{n\to \infty }\left[\left(1+{\frac {1}{n}}\right)^{n}\right]^{x}\\[6pt]&=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{nx}\\[6pt]&=\lim _{n\to \infty }\left(1+{\frac {x}{nx}}\right)^{nx}\\[6pt]&=\lim _{m\to \infty }\left(1+{\frac {x}{m}}\right)^{m}.\end{aligned}}$

Michael Hardy (talk) 13:18, 23 February 2010 (UTC)

Also, I suggest you the following alternative path.

1. Prove that for all real x the sequence (1+x/n)ⁿ (n a positive integer) is eventually increasing; precisely, as soon as n>-x (use the inequality between the arithmetic and geometric means).

2. Prove that it is bounded (just observe that 0≤(1+x/n)ⁿ(1-x/n)ⁿ≤1 as soon as n>|x| and use 1).

3. Therefore it converges for any real x: define exp(x) to be the limit of (1+x/n)ⁿ as n tends to infinity.

4. Prove that if x_n→x then also (1+x_n/n)ⁿ→exp(x).

5. Use 4 to prove exp(x)exp(y)=exp(x+y) for all x and y, which justifes the notation exp(x)=e^x.

6. Prove that exp:R→R₊ is increasing and bijective, define the inverse to be log(x) ("natural logarithm").

7. Prove that log(x)=∫₁^x dt/t for all x>0.

8. Prove that exp(x) is the sum of the exponential series.

(...) --pma 16:13, 23 February 2010 (UTC)

In 5 it should be exp(x+y)=exp(x)exp(y), of course. -- Meni Rosenfeld (talk) 16:47, 23 February 2010 (UTC) whatth...corrected! --pma 20:56, 23 February 2010 (UTC)

Square roots

How would I be able to approximate a square root, like (5.23)^.5, with a taylor series. I know the Taylor series for (1+x)^(1/2), but that only converges for 0<x<1... —Preceding unsigned comment added by 173.179.59.66 (talk) 12:49, 23 February 2010 (UTC)

Well you can always approximate the square root of the inverse of x and then invert again as the series converges for |x| < 1. The convergence will be slow though. Why do you want to do it and why is using the Taylor series important since most any calculator will give the result? Dmcq (talk) 13:07, 23 February 2010 (UTC)

You might expand about the point 5.29 = 2.3² rather than about 0. Michael Hardy (talk) 13:30, 23 February 2010 (UTC)

See also Methods of computing square roots#Taylor series. -- Meni Rosenfeld (talk) 13:34, 23 February 2010 (UTC)

The square root of 5.23 was just an example. Actually, I question was inspired by how calculator's are able to evaluate roots, which I believe is through a Taylor series. Is there a way to write a taylor series for the expression (a+x)^1/2?

A calculator almost certainly would not use the Taylor series. That article Methods of computing square roots says calculators would normally do it via log and exp. Dmcq (talk) 23:06, 23 February 2010 (UTC)

Ooh okay, didn't see that article. But one last question (to make sure that I understand Taylor series), is the equation

${\sqrt {N^{2}+d}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!d^{n}}{(1-2n)n!^{2}4^{n}N^{2n-1}}}=N+{\frac {d}{2N}}-{\frac {d^{2}}{8N^{3}}}+{\frac {d^{3}}{16N^{5}}}-{\frac {5d^{4}}{128N^{7}}}+\cdots$

exact for all d<1? —Preceding unsigned comment added by 173.179.59.66 (talk) 02:33, 24 February 2010 (UTC)

It's exact for all $-N^{2}<d<N^{2}$. Anyway, an excellent and simple way to compute square roots is the Babylonian method. -- Meni Rosenfeld (talk) 07:31, 24 February 2010 (UTC)

Integration

How to integrate e^sin(x)? Chirsgayle (talk) 16:36, 23 February 2010 (UTC)

This function has no elementary antiderivative. You can still calculate definite integrals of it numerically. -- Meni Rosenfeld (talk) 16:44, 23 February 2010 (UTC)

You can also calculate antiderivatives of it numerically. E.g. Runge–Kutta or the like. Michael Hardy (talk) 17:46, 23 February 2010 (UTC)

Just curious, but is there any way to show that a particular function, such as the one given here, has no elementary antiderivative, or is it simply a matter of not being able to come up with one using know methods if integration? 58.147.60.130 (talk) 19:39, 23 February 2010 (UTC)

I believe the Risch algorithm can be used for this. -- Meni Rosenfeld (talk) 20:30, 23 February 2010 (UTC)

Digit by digit root calculation

The method for calculating square roots at Methods_of_computing_square_roots#Digit_by_digit_calculation is currently blowing my mind -- although my friends are less impressed having apparently learned it in grade school. At any rate, what is the proof that it works? Also, I see that it can be generalized to nth roots, when n is an integer -- which lets you calculate nth roots when n is rational -- is there any way to generalize again so a similar method can produce roots for any real number? —Preceding unsigned comment added by 71.70.143.134 (talk) 23:04, 23 February 2010 (UTC)

It's easy to see why this is true, but for a rigorous proof you need to be careful with respect to the decimal point (and perhaps some induction). It boils down to having a current guess p and wanting to find x such that $(p+x)^{2}=S$ which means $p^{2}+2px+x^{2}=S$ or equivalently $(2p+x)x=S-p^{2}$. $S-p^{2}$ is what is denoted there c, and $(2p+x)x$ corresponds to $(20p+x)x$ (up to the decimal point). Since you want only one digit at a time, you take the greatest digit x for which $(2p+x)x\leq S-p^{2}$.

I don't think it can be generalized to irrational-order roots in any meaningful way. Using exp and log is the way to go for general powers. -- Meni Rosenfeld (talk) 07:43, 24 February 2010 (UTC)

The hardest Math question

I can not figure this out.

Ralph likes 25 but not 24; he likes 400 but not 300; he likes 144 but not 145. Which does he like:

	10,   50,   124,   200,   1600,  —Preceding unsigned comment added by Skivvyboy-5 (talk • contribs) 07:03, 24 February 2010 (UTC) 

Hint: Think about factors. Rckrone (talk) 07:08, 24 February 2010 (UTC)

<sarcasm>Isn't it obvious? Ralph like numbers for which $(x-350)(2x-289)(2x-49)>0$. So he likes 50, 124 and 1600. </sarcasm>-- Meni Rosenfeld (talk) 07:58, 24 February 2010 (UTC)

Hint: Which of the choices is a perfect square? PST 08:28, 24 February 2010 (UTC)

You should also be aware that there is no such thing as "the hardest question" and that mathematics is broader than that which you may encounter in these sorts of problems; mathematics requires a diverse range of skills (in fact, there exist skills and ideas in mathematics of which people are unaware), and is most certainly not restricted to "pattern-finding" (which is the skill this question tests).

On the same note, the problem is imprecise (to an extent) as Meni Rosenfeld points out; it is likely that the question looks for a property that the numbers 25, 400 and 144 satisfy, but that 24, 300 and 145 do not. However, there are many such properties, and that leaves the solver "guessing" what the questioner intends (put differently, this question is essentially a test of one's guessing ability rather than one's ability to think mathematically). Given that there are only certain "types of numbers" of which potential solvers are aware (such as "perfect squares", "prime numbers" etc.), a solver can be somewhat certain that his/her guess as to what the questioner intends is correct.

Succinctly, it is not necessarily a "bad question" but you should be aware that it does not really require mathematics to solve. In fact, it is helpful to be aware of this, because if you approach these questions by not "thinking too hard", you should arrive at the answer quickly, but if you do think too hard, you are likely to not be "guessing", and "guessing" is what many of these questions test. PST 08:28, 24 February 2010 (UTC)

For those who intend to criticize the above post: I included a response to the OP (a hint) before digressing on another topic, and thus the OP can decide whether or not he/she will read the post subsequent to the hint. Irrespective of whether he/she does so, his/her question will be answered upon reading the first nine words of my post (the hint). PST 08:33, 24 February 2010 (UTC)

multivariable simultaneous algebra

This one problem is stumping me. I'm supposed to solve for K and a.

$4.4781={K}\times 400^{a}$

$2.2581={K}\times 200^{a}$

I'm interested in how you would do this, not only the answer. Thank you very much! 198.188.150.134 (talk) 08:54, 24 February 2010 (UTC)