Principal component analysis
| Part of a series on |
| Machine learning and data mining |
|---|
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
The data is linearly transformed onto a new coordinate system such that the directions (principal components) capturing the largest variation in the data can be easily identified.
The principal components of a collection of points in a real coordinate space are a sequence of unit vectors, where the -th vector is the direction of a line that best fits the data while being orthogonal to the first vectors. Here, a best-fitting line is defined as one that minimizes the average squared perpendicular distance from the points to the line. These directions (i.e., principal components) constitute an orthonormal basis in which different individual dimensions of the data are linearly uncorrelated. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points.[1]

Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science.
Overview
[edit]When performing PCA, the first principal component of a set of variables is the derived variable formed as a linear combination of the original variables that explains the most variance. The second principal component explains the most variance in what is left once the effect of the first component is removed, and we may proceed through iterations until all the variance is explained. PCA is most commonly used when many of the variables are highly correlated with each other and it is desirable to reduce their number to an independent set. The first principal component can equivalently be defined as a direction that maximizes the variance of the projected data. The -th principal component can be taken as a direction orthogonal to the first principal components that maximizes the variance of the projected data.
For either objective, it can be shown that the principal components are eigenvectors of the data's covariance matrix. Thus, the principal components are often computed by eigendecomposition of the data covariance matrix or singular value decomposition of the data matrix. PCA is the simplest of the true eigenvector-based multivariate analyses and is closely related to factor analysis. Factor analysis typically incorporates more domain-specific assumptions about the underlying structure and solves eigenvectors of a slightly different matrix. PCA is also related to canonical correlation analysis (CCA). CCA defines coordinate systems that optimally describe the cross-covariance between two datasets while PCA defines a new orthogonal coordinate system that optimally describes variance in a single dataset.[2][3][4][5] Robust and L1-norm-based variants of standard PCA have also been proposed.[6][7][8][5]
History
[edit]PCA was invented in 1901 by Karl Pearson,[9] as an analogue of the principal axis theorem in mechanics; it was later independently developed and named by Harold Hotelling in the 1930s.[10] Depending on the field of application, it is also named the discrete Karhunen–Loève transform (KLT) in signal processing, the Hotelling transform in multivariate quality control, proper orthogonal decomposition (POD) in mechanical engineering, singular value decomposition (SVD) of X (invented in the last quarter of the 19th century[11]), eigenvalue decomposition (EVD) of XTX in linear algebra, factor analysis (for a discussion of the differences between PCA and factor analysis see Ch. 7 of Jolliffe's Principal Component Analysis),[12] Eckart–Young theorem (Harman, 1960), or empirical orthogonal functions (EOF) in meteorological science (Lorenz, 1956), empirical eigenfunction decomposition (Sirovich, 1987), quasiharmonic modes (Brooks et al., 1988), spectral decomposition in noise and vibration, and empirical modal analysis in structural dynamics.
Intuition
[edit]PCA can be thought of as fitting a p-dimensional ellipsoid to the data, where each axis of the ellipsoid represents a principal component. If some axis of the ellipsoid is small, then the variance along that axis is also small.
To find the axes of the ellipsoid, we must first center the values of each variable in the dataset on 0 by subtracting the mean of the variable's observed values from each of those values. These transformed values are used instead of the original observed values for each of the variables. Then, we compute the covariance matrix of the data and calculate the eigenvalues and corresponding eigenvectors of this covariance matrix. Then we must normalize each of the orthogonal eigenvectors to turn them into unit vectors. Once this is done, each of the mutually-orthogonal unit eigenvectors can be interpreted as an axis of the ellipsoid fitted to the data. This choice of basis will transform the covariance matrix into a diagonalized form, in which the diagonal elements represent the variance of each axis. The proportion of the variance that each eigenvector represents can be calculated by dividing the eigenvalue corresponding to that eigenvector by the sum of all eigenvalues.
Biplots and scree plots (degree of explained variance) are used to interpret findings of the PCA.

Details
[edit]PCA is defined as an orthogonal linear transformation on a real inner product space that transforms the data to a new coordinate system such that the greatest variance by some scalar projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on.[12]
Consider an data matrix, X, with column-wise zero empirical mean (the sample mean of each column has been shifted to zero), where each of the n rows represents a different repetition of the experiment, and each of the p columns gives a particular kind of feature (say, the results from a particular sensor).
Mathematically, the transformation is defined by a set of size of p-dimensional vectors of weights or coefficients that map each row vector of X to a new vector of principal component scores , given by
in such a way that the individual variables of t considered over the data set successively inherit the maximum possible variance from X, with each coefficient vector w constrained to be a unit vector (where is usually selected to be strictly less than to reduce dimensionality).
The above may equivalently be written in matrix form as
where , , and .
First component
[edit]In order to maximize variance, the first weight vector w(1) thus has to satisfy
Equivalently, writing this in matrix form gives
Since w(1) has been defined to be a unit vector, it equivalently also satisfies
The quantity to be maximised can be recognised as a Rayleigh quotient. A standard result for a positive semidefinite matrix such as XTX is that the quotient's maximum possible value is the largest eigenvalue of the matrix, which occurs when w is the corresponding eigenvector.
With w(1) found, the first principal component of a data vector x(i) can then be given as a score t1(i) = x(i) ⋅ w(1) in the transformed co-ordinates, or as the corresponding vector in the original variables, {x(i) ⋅ w(1)} w(1).
Further components
[edit]The k-th component can be found by subtracting the first k − 1 principal components from X:
and then finding the weight vector which extracts the maximum variance from this new data matrix
It turns out that this gives the remaining eigenvectors of XTX, with the maximum values for the quantity in brackets given by their corresponding eigenvalues. Thus the weight vectors are eigenvectors of XTX.
The k-th principal component of a data vector x(i) can therefore be given as a score tk(i) = x(i) ⋅ w(k) in the transformed coordinates, or as the corresponding vector in the space of the original variables, {x(i) ⋅ w(k)} w(k), where w(k) is the kth eigenvector of XTX.
The full principal components decomposition of X can therefore be given as
where W is a p-by-p matrix of weights whose columns are the eigenvectors of XTX. The transpose of W is sometimes called the whitening or sphering transformation. Columns of W multiplied by the square root of corresponding eigenvalues, that is, eigenvectors scaled up by the variances, are called loadings in PCA or in Factor analysis.
Covariances
[edit]XTX itself can be recognized as proportional to the empirical sample covariance matrix of the dataset XT.[12]: 30–31
The sample covariance Q between two of the different principal components over the dataset is given by:
where the eigenvalue property of w(k) has been used to move from line 2 to line 3. However eigenvectors w(j) and w(k) corresponding to eigenvalues of a symmetric matrix are orthogonal (if the eigenvalues are different), or can be orthogonalised (if the vectors happen to share an equal repeated value). The product in the final line is therefore zero; there is no sample covariance between different principal components over the dataset.
Another way to characterise the principal components transformation is therefore as the transformation to coordinates which diagonalise the empirical sample covariance matrix.
In matrix form, the empirical covariance matrix for the original variables can be written
The empirical covariance matrix between the principal components becomes
where Λ is the diagonal matrix of eigenvalues λ(k) of XTX. λ(k) is equal to the sum of the squares over the dataset associated with each component k, that is, λ(k) = Σi tk2(i) = Σi (x(i) ⋅ w(k))2.
Dimensionality reduction
[edit]The transformation T = X W maps a data vector x(i) from an original space of p variables to a new space of p variables which are uncorrelated over the dataset. However, not all the principal components need to be kept. Keeping only the first L principal components, produced by using only the first L eigenvectors, gives the truncated transformation
where the matrix TL now has n rows but only L columns. In other words, PCA learns a linear transformation where the columns of p × L matrix form an orthogonal basis for the L features (the components of representation t) that are decorrelated.[13] By construction, of all the transformed data matrices with only L columns, this score matrix maximises the variance in the original data that has been preserved, while minimising the total squared reconstruction error or .
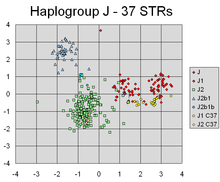
PCA has successfully found linear combinations of the markers that separate out different clusters corresponding to different lines of individuals' Y-chromosomal genetic descent.
Such dimensionality reduction can be a very useful step for visualising and processing high-dimensional datasets, while still retaining as much of the variance in the dataset as possible. For example, selecting L = 2 and keeping only the first two principal components finds the two-dimensional plane through the high-dimensional dataset in which the data is most spread out, so if the data contains clusters these too may be most spread out, and therefore most visible to be plotted out in a two-dimensional diagram; whereas if two directions through the data (or two of the original variables) are chosen at random, the clusters may be much less spread apart from each other, and may in fact be much more likely to substantially overlay each other, making them indistinguishable.
Similarly, in regression analysis, the larger the number of explanatory variables allowed, the greater is the chance of overfitting the model, producing conclusions that fail to generalise to other datasets. One approach, especially when there are strong correlations between different possible explanatory variables, is to reduce them to a few principal components and then run the regression against them, a method called principal component regression.
Dimensionality reduction may also be appropriate when the variables in a dataset are noisy. If each column of the dataset contains independent identically distributed Gaussian noise, then the columns of T will also contain similarly identically distributed Gaussian noise (such a distribution is invariant under the effects of the matrix W, which can be thought of as a high-dimensional rotation of the co-ordinate axes). However, with more of the total variance concentrated in the first few principal components compared to the same noise variance, the proportionate effect of the noise is less—the first few components achieve a higher signal-to-noise ratio. PCA thus can have the effect of concentrating much of the signal into the first few principal components, which can usefully be captured by dimensionality reduction; while the later principal components may be dominated by noise, and so disposed of without great loss. If the dataset is not too large, the significance of the principal components can be tested using parametric bootstrap, as an aid in determining how many principal components to retain.[14]
Singular value decomposition
[edit]The principal components transformation can also be associated with another matrix factorization, the singular value decomposition (SVD) of X,
Here Σ is an n-by-p rectangular diagonal matrix of positive numbers σ(k), called the singular values of X; U is an n-by-n matrix, the columns of which are orthogonal unit vectors of length n called the left singular vectors of X; and W is a p-by-p matrix whose columns are orthogonal unit vectors of length p and called the right singular vectors of X.
In terms of this factorization, the matrix XTX can be written
where is the square diagonal matrix with the singular values of X and the excess zeros chopped off that satisfies . Comparison with the eigenvector factorization of XTX establishes that the right singular vectors W of X are equivalent to the eigenvectors of XTX, while the singular values σ(k) of are equal to the square-root of the eigenvalues λ(k) of XTX.
Using the singular value decomposition the score matrix T can be written
so each column of T is given by one of the left singular vectors of X multiplied by the corresponding singular value. This form is also the polar decomposition of T.
Efficient algorithms exist to calculate the SVD of X without having to form the matrix XTX, so computing the SVD is now the standard way to calculate a principal components analysis from a data matrix,[15] unless only a handful of components are required.
As with the eigen-decomposition, a truncated n × L score matrix TL can be obtained by considering only the first L largest singular values and their singular vectors:
The truncation of a matrix M or T using a truncated singular value decomposition in this way produces a truncated matrix that is the nearest possible matrix of rank L to the original matrix, in the sense of the difference between the two having the smallest possible Frobenius norm, a result known as the Eckart–Young theorem [1936].
Further considerations
[edit]The singular values (in Σ) are the square roots of the eigenvalues of the matrix XTX. Each eigenvalue is proportional to the portion of the "variance" (more correctly of the sum of the squared distances of the points from their multidimensional mean) that is associated with each eigenvector. The sum of all the eigenvalues is equal to the sum of the squared distances of the points from their multidimensional mean. PCA essentially rotates the set of points around their mean in order to align with the principal components. This moves as much of the variance as possible (using an orthogonal transformation) into the first few dimensions. The values in the remaining dimensions, therefore, tend to be small and may be dropped with minimal loss of information (see below). PCA is often used in this manner for dimensionality reduction. PCA has the distinction of being the optimal orthogonal transformation for keeping the subspace that has largest "variance" (as defined above). This advantage, however, comes at the price of greater computational requirements if compared, for example, and when applicable, to the discrete cosine transform, and in particular to the DCT-II which is simply known as the "DCT". Nonlinear dimensionality reduction techniques tend to be more computationally demanding than PCA.
PCA is sensitive to the scaling of the variables. If we have just two variables and they have the same sample variance and are completely correlated, then the PCA will entail a rotation by 45° and the "weights" (they are the cosines of rotation) for the two variables with respect to the principal component will be equal. But if we multiply all values of the first variable by 100, then the first principal component will be almost the same as that variable, with a small contribution from the other variable, whereas the second component will be almost aligned with the second original variable. This means that whenever the different variables have different units (like temperature and mass), PCA is a somewhat arbitrary method of analysis. (Different results would be obtained if one used Fahrenheit rather than Celsius for example.) Pearson's original paper was entitled "On Lines and Planes of Closest Fit to Systems of Points in Space" – "in space" implies physical Euclidean space where such concerns do not arise. One way of making the PCA less arbitrary is to use variables scaled so as to have unit variance, by standardizing the data and hence use the autocorrelation matrix instead of the autocovariance matrix as a basis for PCA. However, this compresses (or expands) the fluctuations in all dimensions of the signal space to unit variance.
Mean subtraction (a.k.a. "mean centering") is necessary for performing classical PCA to ensure that the first principal component describes the direction of maximum variance. If mean subtraction is not performed, the first principal component might instead correspond more or less to the mean of the data. A mean of zero is needed for finding a basis that minimizes the mean square error of the approximation of the data.[16]
Mean-centering is unnecessary if performing a principal components analysis on a correlation matrix, as the data are already centered after calculating correlations. Correlations are derived from the cross-product of two standard scores (Z-scores) or statistical moments (hence the name: Pearson Product-Moment Correlation). Also see the article by Kromrey & Foster-Johnson (1998) on "Mean-centering in Moderated Regression: Much Ado About Nothing". Since covariances are correlations of normalized variables (Z- or standard-scores) a PCA based on the correlation matrix of X is equal to a PCA based on the covariance matrix of Z, the standardized version of X.
PCA is a popular primary technique in pattern recognition. It is not, however, optimized for class separability.[17] However, it has been used to quantify the distance between two or more classes by calculating center of mass for each class in principal component space and reporting Euclidean distance between center of mass of two or more classes.[18] The linear discriminant analysis is an alternative which is optimized for class separability.
Table of symbols and abbreviations
[edit]| Symbol | Meaning | Dimensions | Indices |
|---|---|---|---|
| data matrix, consisting of the set of all data vectors, one vector per row | | ||
| the number of row vectors in the data set | scalar | ||
| the number of elements in each row vector (dimension) | scalar | ||
| the number of dimensions in the dimensionally reduced subspace, | scalar | ||
| vector of empirical means, one mean for each column j of the data matrix | |||
| vector of empirical standard deviations, one standard deviation for each column j of the data matrix | |||
| vector of all 1's | |||
| deviations from the mean of each column j of the data matrix | | ||
| z-scores, computed using the mean and standard deviation for each column j of the data matrix | | ||
| covariance matrix | | ||
| correlation matrix | | ||
| matrix consisting of the set of all eigenvectors of C, one eigenvector per column | | ||
| diagonal matrix consisting of the set of all eigenvalues of C along its principal diagonal, and 0 for all other elements ( note used above ) | | ||
| matrix of basis vectors, one vector per column, where each basis vector is one of the eigenvectors of C, and where the vectors in W are a sub-set of those in V | | ||
| matrix consisting of n row vectors, where each vector is the projection of the corresponding data vector from matrix X onto the basis vectors contained in the columns of matrix W. | |
Properties and limitations
[edit]Properties
[edit]Some properties of PCA include:[12][page needed]
- Property 1: For any integer q, 1 ≤ q ≤ p, consider the orthogonal linear transformation
- where is a q-element vector and is a (q × p) matrix, and let be the variance-covariance matrix for . Then the trace of , denoted , is maximized by taking , where consists of the first q columns of is the transpose of . ( is not defined here)
- Property 2: Consider again the orthonormal transformation
- with and defined as before. Then is minimized by taking where consists of the last q columns of .
The statistical implication of this property is that the last few PCs are not simply unstructured left-overs after removing the important PCs. Because these last PCs have variances as small as possible they are useful in their own right. They can help to detect unsuspected near-constant linear relationships between the elements of x, and they may also be useful in regression, in selecting a subset of variables from x, and in outlier detection.
- Property 3: (Spectral decomposition of Σ)
Before we look at its usage, we first look at diagonal elements,
Then, perhaps the main statistical implication of the result is that not only can we decompose the combined variances of all the elements of x into decreasing contributions due to each PC, but we can also decompose the whole covariance matrix into contributions from each PC. Although not strictly decreasing, the elements of will tend to become smaller as increases, as is nonincreasing for increasing , whereas the elements of tend to stay about the same size because of the normalization constraints: .
Limitations
[edit]As noted above, the results of PCA depend on the scaling of the variables. This can be cured by scaling each feature by its standard deviation, so that one ends up with dimensionless features with unital variance.[19]
The applicability of PCA as described above is limited by certain (tacit) assumptions[20] made in its derivation. In particular, PCA can capture linear correlations between the features but fails when this assumption is violated (see Figure 6a in the reference). In some cases, coordinate transformations can restore the linearity assumption and PCA can then be applied (see kernel PCA).
Another limitation is the mean-removal process before constructing the covariance matrix for PCA. In fields such as astronomy, all the signals are non-negative, and the mean-removal process will force the mean of some astrophysical exposures to be zero, which consequently creates unphysical negative fluxes,[21] and forward modeling has to be performed to recover the true magnitude of the signals.[22] As an alternative method, non-negative matrix factorization focusing only on the non-negative elements in the matrices, which is well-suited for astrophysical observations.[23][24][25] See more at Relation between PCA and Non-negative Matrix Factorization.
PCA is at a disadvantage if the data has not been standardized before applying the algorithm to it. PCA transforms original data into data that is relevant to the principal components of that data, which means that the new data variables cannot be interpreted in the same ways that the originals were. They are linear interpretations of the original variables. Also, if PCA is not performed properly, there is a high likelihood of information loss.[26]
PCA relies on a linear model. If a dataset has a pattern hidden inside it that is nonlinear, then PCA can actually steer the analysis in the complete opposite direction of progress.[27][page needed] Researchers at Kansas State University discovered that the sampling error in their experiments impacted the bias of PCA results. "If the number of subjects or blocks is smaller than 30, and/or the researcher is interested in PC's beyond the first, it may be better to first correct for the serial correlation, before PCA is conducted".[28] The researchers at Kansas State also found that PCA could be "seriously biased if the autocorrelation structure of the data is not correctly handled".[28]
PCA and information theory
[edit]Dimensionality reduction results in a loss of information, in general. PCA-based dimensionality reduction tends to minimize that information loss, under certain signal and noise models.
Under the assumption that
that is, that the data vector is the sum of the desired information-bearing signal and a noise signal one can show that PCA can be optimal for dimensionality reduction, from an information-theoretic point-of-view.
In particular, Linsker showed that if is Gaussian and is Gaussian noise with a covariance matrix proportional to the identity matrix, the PCA maximizes the mutual information between the desired information and the dimensionality-reduced output .[29]
If the noise is still Gaussian and has a covariance matrix proportional to the identity matrix (that is, the components of the vector are iid), but the information-bearing signal is non-Gaussian (which is a common scenario), PCA at least minimizes an upper bound on the information loss, which is defined as[30][31]
The optimality of PCA is also preserved if the noise is iid and at least more Gaussian (in terms of the Kullback–Leibler divergence) than the information-bearing signal .[32] In general, even if the above signal model holds, PCA loses its information-theoretic optimality as soon as the noise becomes dependent.
Computation using the covariance method
[edit]The following is a detailed description of PCA using the covariance method[33] as opposed to the correlation method.[34]
The goal is to transform a given data set X of dimension p to an alternative data set Y of smaller dimension L. Equivalently, we are seeking to find the matrix Y, where Y is the Karhunen–Loève transform (KLT) of matrix X:
-
Organize the data set
Suppose you have data comprising a set of observations of p variables, and you want to reduce the data so that each observation can be described with only L variables, L < p. Suppose further, that the data are arranged as a set of n data vectors with each representing a single grouped observation of the p variables.
- Write as row vectors, each with p elements.
- Place the row vectors into a single matrix X of dimensions n × p.
-
Calculate the empirical mean
- Find the empirical mean along each column j = 1, ..., p.
- Place the calculated mean values into an empirical mean vector u of dimensions p × 1.
-
Calculate the deviations from the mean
Mean subtraction is an integral part of the solution towards finding a principal component basis that minimizes the mean square error of approximating the data.[35] Hence we proceed by centering the data as follows:
- Subtract the empirical mean vector from each row of the data matrix X.
- Store mean-subtracted data in the n × p matrix B. where h is an n × 1 column vector of all 1s:
In some applications, each variable (column of B) may also be scaled to have a variance equal to 1 (see Z-score).[36] This step affects the calculated principal components, but makes them independent of the units used to measure the different variables.
-
Find the covariance matrix
- Find the p × p empirical covariance matrix C from matrix B: where is the conjugate transpose operator. If B consists entirely of real numbers, which is the case in many applications, the "conjugate transpose" is the same as the regular transpose.
- The reasoning behind using n − 1 instead of n to calculate the covariance is Bessel's correction.
-
Find the eigenvectors and eigenvalues of the covariance matrix
- Compute the matrix V of eigenvectors which diagonalizes the covariance matrix C: where D is the diagonal matrix of eigenvalues of C. This step will typically involve the use of a computer-based algorithm for computing eigenvectors and eigenvalues. These algorithms are readily available as sub-components of most matrix algebra systems, such as SAS,[37] R, MATLAB,[38][39] Mathematica,[40] SciPy, IDL (Interactive Data Language), or GNU Octave as well as OpenCV.
- Matrix D will take the form of an p × p diagonal matrix, where is the jth eigenvalue of the covariance matrix C, and
- Matrix V, also of dimension p × p, contains p column vectors, each of length p, which represent the p eigenvectors of the covariance matrix C.
- The eigenvalues and eigenvectors are ordered and paired. The jth eigenvalue corresponds to the jth eigenvector.
- Matrix V denotes the matrix of right eigenvectors (as opposed to left eigenvectors). In general, the matrix of right eigenvectors need not be the (conjugate) transpose of the matrix of left eigenvectors.
-
Rearrange the eigenvectors and eigenvalues
- Sort the columns of the eigenvector matrix V and eigenvalue matrix D in order of decreasing eigenvalue.
- Make sure to maintain the correct pairings between the columns in each matrix.
-
Compute the cumulative energy content for each eigenvector
- The eigenvalues represent the distribution of the source data's energy[clarification needed] among each of the eigenvectors, where the eigenvectors form a basis for the data. The cumulative energy content g for the jth eigenvector is the sum of the energy content across all of the eigenvalues from 1 through j:[citation needed]
-
Select a subset of the eigenvectors as basis vectors
- Save the first L columns of V as the p × L matrix W: where
- Use the vector g as a guide in choosing an appropriate value for L. The goal is to choose a value of L as small as possible while achieving a reasonably high value of g on a percentage basis. For example, you may want to choose L so that the cumulative energy g is above a certain threshold, like 90 percent. In this case, choose the smallest value of L such that
-
Project the data onto the new basis
- The projected data points are the rows of the matrix
Derivation using the covariance method
[edit]Let X be a d-dimensional random vector expressed as column vector. Without loss of generality, assume X has zero mean.
We want to find a d × d orthonormal transformation matrix P so that PX has a diagonal covariance matrix (that is, PX is a random vector with all its distinct components pairwise uncorrelated).
A quick computation assuming were unitary yields:
Hence holds if and only if were diagonalisable by .
This is very constructive, as cov(X) is guaranteed to be a non-negative definite matrix and thus is guaranteed to be diagonalisable by some unitary matrix.
Covariance-free computation
[edit]In practical implementations, especially with high dimensional data (large p), the naive covariance method is rarely used because it is not efficient due to high computational and memory costs of explicitly determining the covariance matrix. The covariance-free approach avoids the np2 operations of explicitly calculating and storing the covariance matrix XTX, instead utilizing one of matrix-free methods, for example, based on the function evaluating the product XT(X r) at the cost of 2np operations.
Iterative computation
[edit]One way to compute the first principal component efficiently[41] is shown in the following pseudo-code, for a data matrix X with zero mean, without ever computing its covariance matrix.
r = a random vector of length p r = r / norm(r) do c times: s = 0 (a vector of length p) for each row x in X s = s + (x ⋅ r) x λ = rTs // λ is the eigenvalue error = |λ ⋅ r − s| r = s / norm(s) exit if error < tolerance return λ, r
This power iteration algorithm simply calculates the vector XT(X r), normalizes, and places the result back in r. The eigenvalue is approximated by rT (XTX) r, which is the Rayleigh quotient on the unit vector r for the covariance matrix XTX . If the largest singular value is well separated from the next largest one, the vector r gets close to the first principal component of X within the number of iterations c, which is small relative to p, at the total cost 2cnp. The power iteration convergence can be accelerated without noticeably sacrificing the small cost per iteration using more advanced matrix-free methods, such as the Lanczos algorithm or the Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) method.
Subsequent principal components can be computed one-by-one via deflation or simultaneously as a block. In the former approach, imprecisions in already computed approximate principal components additively affect the accuracy of the subsequently computed principal components, thus increasing the error with every new computation. The latter approach in the block power method replaces single-vectors r and s with block-vectors, matrices R and S. Every column of R approximates one of the leading principal components, while all columns are iterated simultaneously. The main calculation is evaluation of the product XT(X R). Implemented, for example, in LOBPCG, efficient blocking eliminates the accumulation of the errors, allows using high-level BLAS matrix-matrix product functions, and typically leads to faster convergence, compared to the single-vector one-by-one technique.
The NIPALS method
[edit]Non-linear iterative partial least squares (NIPALS) is a variant the classical power iteration with matrix deflation by subtraction implemented for computing the first few components in a principal component or partial least squares analysis. For very-high-dimensional datasets, such as those generated in the *omics sciences (for example, genomics, metabolomics) it is usually only necessary to compute the first few PCs. The non-linear iterative partial least squares (NIPALS) algorithm updates iterative approximations to the leading scores and loadings t1 and r1T by the power iteration multiplying on every iteration by X on the left and on the right, that is, calculation of the covariance matrix is avoided, just as in the matrix-free implementation of the power iterations to XTX, based on the function evaluating the product XT(X r) = ((X r)TX)T.
The matrix deflation by subtraction is performed by subtracting the outer product, t1r1T from X leaving the deflated residual matrix used to calculate the subsequent leading PCs.[42] For large data matrices, or matrices that have a high degree of column collinearity, NIPALS suffers from loss of orthogonality of PCs due to machine precision round-off errors accumulated in each iteration and matrix deflation by subtraction.[43] A Gram–Schmidt re-orthogonalization algorithm is applied to both the scores and the loadings at each iteration step to eliminate this loss of orthogonality.[44] NIPALS reliance on single-vector multiplications cannot take advantage of high-level BLAS and results in slow convergence for clustered leading singular values—both these deficiencies are resolved in more sophisticated matrix-free block solvers, such as the Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) method.
Online/sequential estimation
[edit]In an "online" or "streaming" situation with data arriving piece by piece rather than being stored in a single batch, it is useful to make an estimate of the PCA projection that can be updated sequentially. This can be done efficiently, but requires different algorithms.[45]
Qualitative variables
[edit]In PCA, it is common that we want to introduce qualitative variables as supplementary elements. For example, many quantitative variables have been measured on plants. For these plants, some qualitative variables are available as, for example, the species to which the plant belongs. These data were subjected to PCA for quantitative variables. When analyzing the results, it is natural to connect the principal components to the qualitative variable species. For this, the following results are produced.
- Identification, on the factorial planes, of the different species, for example, using different colors.
- Representation, on the factorial planes, of the centers of gravity of plants belonging to the same species.
- For each center of gravity and each axis, p-value to judge the significance of the difference between the center of gravity and origin.
These results are what is called introducing a qualitative variable as supplementary element. This procedure is detailed in and Husson, Lê & Pagès 2009 and Pagès 2013. Few software offer this option in an "automatic" way. This is the case of SPAD that historically, following the work of Ludovic Lebart, was the first to propose this option, and the R package FactoMineR.
Applications
[edit]Intelligence
[edit]The earliest application of factor analysis was in locating and measuring components of human intelligence. It was believed that intelligence had various uncorrelated components such as spatial intelligence, verbal intelligence, induction, deduction etc and that scores on these could be adduced by factor analysis from results on various tests, to give a single index known as the Intelligence Quotient (IQ). The pioneering statistical psychologist Spearman actually developed factor analysis in 1904 for his two-factor theory of intelligence, adding a formal technique to the science of psychometrics. In 1924 Thurstone looked for 56 factors of intelligence, developing the notion of Mental Age. Standard IQ tests today are based on this early work.[46]
Residential differentiation
[edit]In 1949, Shevky and Williams introduced the theory of factorial ecology, which dominated studies of residential differentiation from the 1950s to the 1970s.[47] Neighbourhoods in a city were recognizable or could be distinguished from one another by various characteristics which could be reduced to three by factor analysis. These were known as 'social rank' (an index of occupational status), 'familism' or family size, and 'ethnicity'; Cluster analysis could then be applied to divide the city into clusters or precincts according to values of the three key factor variables. An extensive literature developed around factorial ecology in urban geography, but the approach went out of fashion after 1980 as being methodologically primitive and having little place in postmodern geographical paradigms.
One of the problems with factor analysis has always been finding convincing names for the various artificial factors. In 2000, Flood revived the factorial ecology approach to show that principal components analysis actually gave meaningful answers directly, without resorting to factor rotation. The principal components were actually dual variables or shadow prices of 'forces' pushing people together or apart in cities. The first component was 'accessibility', the classic trade-off between demand for travel and demand for space, around which classical urban economics is based. The next two components were 'disadvantage', which keeps people of similar status in separate neighbourhoods (mediated by planning), and ethnicity, where people of similar ethnic backgrounds try to co-locate.[48]
About the same time, the Australian Bureau of Statistics defined distinct indexes of advantage and disadvantage taking the first principal component of sets of key variables that were thought to be important. These SEIFA indexes are regularly published for various jurisdictions, and are used frequently in spatial analysis.[49]
Development indexes
[edit]PCA has been the only formal method available for the development of indexes, which are otherwise a hit-or-miss ad hoc undertaking.
The City Development Index was developed by PCA from about 200 indicators of city outcomes in a 1996 survey of 254 global cities. The first principal component was subject to iterative regression, adding the original variables singly until about 90% of its variation was accounted for. The index ultimately used about 15 indicators but was a good predictor of many more variables. Its comparative value agreed very well with a subjective assessment of the condition of each city. The coefficients on items of infrastructure were roughly proportional to the average costs of providing the underlying services, suggesting the Index was actually a measure of effective physical and social investment in the city.
The country-level Human Development Index (HDI) from UNDP, which has been published since 1990 and is very extensively used in development studies,[50] has very similar coefficients on similar indicators, strongly suggesting it was originally constructed using PCA.
Population genetics
[edit]In 1978 Cavalli-Sforza and others pioneered the use of principal components analysis (PCA) to summarise data on variation in human gene frequencies across regions. The components showed distinctive patterns, including gradients and sinusoidal waves. They interpreted these patterns as resulting from specific ancient migration events.
Since then, PCA has been ubiquitous in population genetics, with thousands of papers using PCA as a display mechanism. Genetics varies largely according to proximity, so the first two principal components actually show spatial distribution and may be used to map the relative geographical location of different population groups, thereby showing individuals who have wandered from their original locations.[51]
PCA in genetics has been technically controversial, in that the technique has been performed on discrete non-normal variables and often on binary allele markers. The lack of any measures of standard error in PCA are also an impediment to more consistent usage. In August 2022, the molecular biologist Eran Elhaik published a theoretical paper in Scientific Reports analyzing 12 PCA applications. He concluded that it was easy to manipulate the method, which, in his view, generated results that were 'erroneous, contradictory, and absurd.' Specifically, he argued, the results achieved in population genetics were characterized by cherry-picking and circular reasoning.[52]
Market research and indexes of attitude
[edit]Market research has been an extensive user of PCA. It is used to develop customer satisfaction or customer loyalty scores for products, and with clustering, to develop market segments that may be targeted with advertising campaigns, in much the same way as factorial ecology will locate geographical areas with similar characteristics.[53]
PCA rapidly transforms large amounts of data into smaller, easier-to-digest variables that can be more rapidly and readily analyzed. In any consumer questionnaire, there are series of questions designed to elicit consumer attitudes, and principal components seek out latent variables underlying these attitudes. For example, the Oxford Internet Survey in 2013 asked 2000 people about their attitudes and beliefs, and from these analysts extracted four principal component dimensions, which they identified as 'escape', 'social networking', 'efficiency', and 'problem creating'.[54]
Another example from Joe Flood in 2008 extracted an attitudinal index toward housing from 28 attitude questions in a national survey of 2697 households in Australia. The first principal component represented a general attitude toward property and home ownership. The index, or the attitude questions it embodied, could be fed into a General Linear Model of tenure choice. The strongest determinant of private renting by far was the attitude index, rather than income, marital status or household type.[55]
Quantitative finance
[edit]In quantitative finance, PCA is used[56] in financial risk management, and has been applied to other problems such as portfolio optimization.
PCA is commonly used in problems involving fixed income securities and portfolios, and interest rate derivatives. Valuations here depend on the entire yield curve, comprising numerous highly correlated instruments, and PCA is used to define a set of components or factors that explain rate movements,[57] thereby facilitating the modelling. One common risk management application is to calculating value at risk, VaR, applying PCA to the Monte Carlo simulation. [58] Here, for each simulation-sample, the components are stressed, and rates, and in turn option values, are then reconstructed; with VaR calculated, finally, over the entire run. PCA is also used in hedging exposure to interest rate risk, given partial durations and other sensitivities. [57] Under both, the first three, typically, principal components of the system are of interest (representing "shift", "twist", and "curvature"). These principal components are derived from an eigen-decomposition of the covariance matrix of yield at predefined maturities; [59] and where the variance of each component is its eigenvalue (and as the components are orthogonal, no correlation need be incorporated in subsequent modelling).
For equity, an optimal portfolio is one where the expected return is maximized for a given level of risk, or alternatively, where risk is minimized for a given return; see Markowitz model for discussion. Thus, one approach is to reduce portfolio risk, where allocation strategies are applied to the "principal portfolios" instead of the underlying stocks. A second approach is to enhance portfolio return, using the principal components to select companies' stocks with upside potential. [60] [61] PCA has also been used to understand relationships [56] between international equity markets, and within markets between groups of companies in industries or sectors.
PCA may also be applied to stress testing,[62] essentially an analysis of a bank's ability to endure a hypothetical adverse economic scenario. Its utility is in "distilling the information contained in [several] macroeconomic variables into a more manageable data set, which can then [be used] for analysis."[62] Here, the resulting factors are linked to e.g. interest rates – based on the largest elements of the factor's eigenvector – and it is then observed how a "shock" to each of the factors affects the implied assets of each of the banks.
Neuroscience
[edit]A variant of principal components analysis is used in neuroscience to identify the specific properties of a stimulus that increases a neuron's probability of generating an action potential.[63][64] This technique is known as spike-triggered covariance analysis. In a typical application an experimenter presents a white noise process as a stimulus (usually either as a sensory input to a test subject, or as a current injected directly into the neuron) and records a train of action potentials, or spikes, produced by the neuron as a result. Presumably, certain features of the stimulus make the neuron more likely to spike. In order to extract these features, the experimenter calculates the covariance matrix of the spike-triggered ensemble, the set of all stimuli (defined and discretized over a finite time window, typically on the order of 100 ms) that immediately preceded a spike. The eigenvectors of the difference between the spike-triggered covariance matrix and the covariance matrix of the prior stimulus ensemble (the set of all stimuli, defined over the same length time window) then indicate the directions in the space of stimuli along which the variance of the spike-triggered ensemble differed the most from that of the prior stimulus ensemble. Specifically, the eigenvectors with the largest positive eigenvalues correspond to the directions along which the variance of the spike-triggered ensemble showed the largest positive change compared to the variance of the prior. Since these were the directions in which varying the stimulus led to a spike, they are often good approximations of the sought after relevant stimulus features.
In neuroscience, PCA is also used to discern the identity of a neuron from the shape of its action potential. Spike sorting is an important procedure because extracellular recording techniques often pick up signals from more than one neuron. In spike sorting, one first uses PCA to reduce the dimensionality of the space of action potential waveforms, and then performs clustering analysis to associate specific action potentials with individual neurons.
PCA as a dimension reduction technique is particularly suited to detect coordinated activities of large neuronal ensembles. It has been used in determining collective variables, that is, order parameters, during phase transitions in the brain.[65]
Relation with other methods
[edit]Correspondence analysis
[edit]Correspondence analysis (CA) was developed by Jean-Paul Benzécri[66] and is conceptually similar to PCA, but scales the data (which should be non-negative) so that rows and columns are treated equivalently. It is traditionally applied to contingency tables. CA decomposes the chi-squared statistic associated to this table into orthogonal factors.[67] Because CA is a descriptive technique, it can be applied to tables for which the chi-squared statistic is appropriate or not. Several variants of CA are available including detrended correspondence analysis and canonical correspondence analysis. One special extension is multiple correspondence analysis, which may be seen as the counterpart of principal component analysis for categorical data.[68]
Factor analysis
[edit]
Principal component analysis creates variables that are linear combinations of the original variables. The new variables have the property that the variables are all orthogonal. The PCA transformation can be helpful as a pre-processing step before clustering. PCA is a variance-focused approach seeking to reproduce the total variable variance, in which components reflect both common and unique variance of the variable. PCA is generally preferred for purposes of data reduction (that is, translating variable space into optimal factor space) but not when the goal is to detect the latent construct or factors.
Factor analysis is similar to principal component analysis, in that factor analysis also involves linear combinations of variables. Different from PCA, factor analysis is a correlation-focused approach seeking to reproduce the inter-correlations among variables, in which the factors "represent the common variance of variables, excluding unique variance".[69] In terms of the correlation matrix, this corresponds with focusing on explaining the off-diagonal terms (that is, shared co-variance), while PCA focuses on explaining the terms that sit on the diagonal. However, as a side result, when trying to reproduce the on-diagonal terms, PCA also tends to fit relatively well the off-diagonal correlations.[12]: 158 Results given by PCA and factor analysis are very similar in most situations, but this is not always the case, and there are some problems where the results are significantly different. Factor analysis is generally used when the research purpose is detecting data structure (that is, latent constructs or factors) or causal modeling. If the factor model is incorrectly formulated or the assumptions are not met, then factor analysis will give erroneous results.[70]
K-means clustering
[edit]It has been asserted that the relaxed solution of k-means clustering, specified by the cluster indicators, is given by the principal components, and the PCA subspace spanned by the principal directions is identical to the cluster centroid subspace.[71][72] However, that PCA is a useful relaxation of k-means clustering was not a new result,[73] and it is straightforward to uncover counterexamples to the statement that the cluster centroid subspace is spanned by the principal directions.[74]
Non-negative matrix factorization
[edit]
Non-negative matrix factorization (NMF) is a dimension reduction method where only non-negative elements in the matrices are used, which is therefore a promising method in astronomy,[23][24][25] in the sense that astrophysical signals are non-negative. The PCA components are orthogonal to each other, while the NMF components are all non-negative and therefore constructs a non-orthogonal basis.
In PCA, the contribution of each component is ranked based on the magnitude of its corresponding eigenvalue, which is equivalent to the fractional residual variance (FRV) in analyzing empirical data.[21] For NMF, its components are ranked based only on the empirical FRV curves.[25] The residual fractional eigenvalue plots, that is, as a function of component number given a total of components, for PCA have a flat plateau, where no data is captured to remove the quasi-static noise, then the curves drop quickly as an indication of over-fitting (random noise).[21] The FRV curves for NMF is decreasing continuously[25] when the NMF components are constructed sequentially,[24] indicating the continuous capturing of quasi-static noise; then converge to higher levels than PCA,[25] indicating the less over-fitting property of NMF.
Iconography of correlations
[edit]It is often difficult to interpret the principal components when the data include many variables of various origins, or when some variables are qualitative. This leads the PCA user to a delicate elimination of several variables. If observations or variables have an excessive impact on the direction of the axes, they should be removed and then projected as supplementary elements. In addition, it is necessary to avoid interpreting the proximities between the points close to the center of the factorial plane.
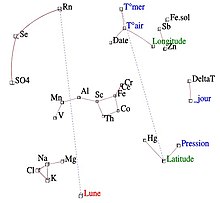
The iconography of correlations, on the contrary, which is not a projection on a system of axes, does not have these drawbacks. We can therefore keep all the variables.
The principle of the diagram is to underline the "remarkable" correlations of the correlation matrix, by a solid line (positive correlation) or dotted line (negative correlation).
A strong correlation is not "remarkable" if it is not direct, but caused by the effect of a third variable. Conversely, weak correlations can be "remarkable". For example, if a variable Y depends on several independent variables, the correlations of Y with each of them are weak and yet "remarkable".
Generalizations
[edit]Sparse PCA
[edit]A particular disadvantage of PCA is that the principal components are usually linear combinations of all input variables. Sparse PCA overcomes this disadvantage by finding linear combinations that contain just a few input variables. It extends the classic method of principal component analysis (PCA) for the reduction of dimensionality of data by adding sparsity constraint on the input variables. Several approaches have been proposed, including
- a regression framework,[75]
- a convex relaxation/semidefinite programming framework,[76]
- a generalized power method framework[77]
- an alternating maximization framework[78]
- forward-backward greedy search and exact methods using branch-and-bound techniques,[79]
- Bayesian formulation framework.[80]
The methodological and theoretical developments of Sparse PCA as well as its applications in scientific studies were recently reviewed in a survey paper.[81]
Nonlinear PCA
[edit]
Most of the modern methods for nonlinear dimensionality reduction find their theoretical and algorithmic roots in PCA or K-means. Pearson's original idea was to take a straight line (or plane) which will be "the best fit" to a set of data points. Trevor Hastie expanded on this concept by proposing Principal curves[85] as the natural extension for the geometric interpretation of PCA, which explicitly constructs a manifold for data approximation followed by projecting the points onto it. See also the elastic map algorithm and principal geodesic analysis.[86] Another popular generalization is kernel PCA, which corresponds to PCA performed in a reproducing kernel Hilbert space associated with a positive definite kernel.
In multilinear subspace learning,[87][88][89] PCA is generalized to multilinear PCA (MPCA) that extracts features directly from tensor representations. MPCA is solved by performing PCA in each mode of the tensor iteratively. MPCA has been applied to face recognition, gait recognition, etc. MPCA is further extended to uncorrelated MPCA, non-negative MPCA and robust MPCA.
N-way principal component analysis may be performed with models such as Tucker decomposition, PARAFAC, multiple factor analysis, co-inertia analysis, STATIS, and DISTATIS.
Robust PCA
[edit]While PCA finds the mathematically optimal method (as in minimizing the squared error), it is still sensitive to outliers in the data that produce large errors, something that the method tries to avoid in the first place. It is therefore common practice to remove outliers before computing PCA. However, in some contexts, outliers can be difficult to identify. For example, in data mining algorithms like correlation clustering, the assignment of points to clusters and outliers is not known beforehand. A recently proposed generalization of PCA[90] based on a weighted PCA increases robustness by assigning different weights to data objects based on their estimated relevancy.
Outlier-resistant variants of PCA have also been proposed, based on L1-norm formulations (L1-PCA).[6][4]
Robust principal component analysis (RPCA) via decomposition in low-rank and sparse matrices is a modification of PCA that works well with respect to grossly corrupted observations.[91][92][93]
Similar techniques
[edit]Independent component analysis
[edit]Independent component analysis (ICA) is directed to similar problems as principal component analysis, but finds additively separable components rather than successive approximations.
Network component analysis
[edit]Given a matrix , it tries to decompose it into two matrices such that . A key difference from techniques such as PCA and ICA is that some of the entries of are constrained to be 0. Here is termed the regulatory layer. While in general such a decomposition can have multiple solutions, they prove that if the following conditions are satisfied :
- has full column rank
- Each column of must have at least zeroes where is the number of columns of (or alternatively the number of rows of ). The justification for this criterion is that if a node is removed from the regulatory layer along with all the output nodes connected to it, the result must still be characterized by a connectivity matrix with full column rank.
- must have full row rank.
then the decomposition is unique up to multiplication by a scalar.[94]
Discriminant analysis of principal components
[edit]Discriminant analysis of principal components (DAPC) is a multivariate method used to identify and describe clusters of genetically related individuals. Genetic variation is partitioned into two components: variation between groups and within groups, and it maximizes the former. Linear discriminants are linear combinations of alleles which best separate the clusters. Alleles that most contribute to this discrimination are therefore those that are the most markedly different across groups. The contributions of alleles to the groupings identified by DAPC can allow identifying regions of the genome driving the genetic divergence among groups[95] In DAPC, data is first transformed using a principal components analysis (PCA) and subsequently clusters are identified using discriminant analysis (DA).
A DAPC can be realized on R using the package Adegenet. (more info: adegenet on the web)
Directional component analysis
[edit]Directional component analysis (DCA) is a method used in the atmospheric sciences for analysing multivariate datasets.[96] Like PCA, it allows for dimension reduction, improved visualization and improved interpretability of large data-sets. Also like PCA, it is based on a covariance matrix derived from the input dataset. The difference between PCA and DCA is that DCA additionally requires the input of a vector direction, referred to as the impact. Whereas PCA maximises explained variance, DCA maximises probability density given impact. The motivation for DCA is to find components of a multivariate dataset that are both likely (measured using probability density) and important (measured using the impact). DCA has been used to find the most likely and most serious heat-wave patterns in weather prediction ensembles ,[97] and the most likely and most impactful changes in rainfall due to climate change .[98]
Software/source code
[edit]- ALGLIB – a C++ and C# library that implements PCA and truncated PCA
- Analytica – The built-in EigenDecomp function computes principal components.
- ELKI – includes PCA for projection, including robust variants of PCA, as well as PCA-based clustering algorithms.
- Gretl – principal component analysis can be performed either via the
pcacommand or via theprincomp()function. - Julia – Supports PCA with the
pcafunction in the MultivariateStats package - KNIME – A java based nodal arranging software for Analysis, in this the nodes called PCA, PCA compute, PCA Apply, PCA inverse make it easily.
- Maple (software) – The PCA command is used to perform a principal component analysis on a set of data.
- Mathematica – Implements principal component analysis with the PrincipalComponents command using both covariance and correlation methods.
- MathPHP – PHP mathematics library with support for PCA.
- MATLAB – The SVD function is part of the basic system. In the Statistics Toolbox, the functions
princompandpca(R2012b) give the principal components, while the functionpcaresgives the residuals and reconstructed matrix for a low-rank PCA approximation. - Matplotlib – Python library have a PCA package in the .mlab module.
- mlpack – Provides an implementation of principal component analysis in C++.
- mrmath – A high performance math library for Delphi and FreePascal can perform PCA; including robust variants.
- NAG Library – Principal components analysis is implemented via the
g03aaroutine (available in both the Fortran versions of the Library). - NMath – Proprietary numerical library containing PCA for the .NET Framework.
- GNU Octave – Free software computational environment mostly compatible with MATLAB, the function
princompgives the principal component. - OpenCV
- Oracle Database 12c – Implemented via
DBMS_DATA_MINING.SVDS_SCORING_MODEby specifying setting valueSVDS_SCORING_PCA - Orange (software) – Integrates PCA in its visual programming environment. PCA displays a scree plot (degree of explained variance) where user can interactively select the number of principal components.
- Origin – Contains PCA in its Pro version.
- Qlucore – Commercial software for analyzing multivariate data with instant response using PCA.
- R – Free statistical package, the functions
princompandprcompcan be used for principal component analysis;prcompuses singular value decomposition which generally gives better numerical accuracy. Some packages that implement PCA in R, include, but are not limited to:ade4,vegan,ExPosition,dimRed, andFactoMineR. - SAS – Proprietary software; for example, see[99]
- scikit-learn – Python library for machine learning which contains PCA, Probabilistic PCA, Kernel PCA, Sparse PCA and other techniques in the decomposition module.
- Scilab – Free and open-source, cross-platform numerical computational package, the function
princompcomputes principal component analysis, the functionpcacomputes principal component analysis with standardized variables. - SPSS – Proprietary software most commonly used by social scientists for PCA, factor analysis and associated cluster analysis.
- Weka – Java library for machine learning which contains modules for computing principal components.
See also
[edit]- Correspondence analysis (for contingency tables)
- Multiple correspondence analysis (for qualitative variables)
- Factor analysis of mixed data (for quantitative and qualitative variables)
- Canonical correlation
- CUR matrix approximation (can replace of low-rank SVD approximation)
- Detrended correspondence analysis
- Directional component analysis
- Dynamic mode decomposition
- Eigenface
- Expectation–maximization algorithm
- Exploratory factor analysis (Wikiversity)
- Factorial code
- Functional principal component analysis
- Geometric data analysis
- Independent component analysis
- Kernel PCA
- L1-norm principal component analysis
- Low-rank approximation
- Matrix decomposition
- Non-negative matrix factorization
- Nonlinear dimensionality reduction
- Oja's rule
- Point distribution model (PCA applied to morphometry and computer vision)
- Principal component analysis (Wikibooks)
- Principal component regression
- Singular spectrum analysis
- Singular value decomposition
- Sparse PCA
- Transform coding
- Weighted least squares
References
[edit]- ^ Jolliffe, Ian T.; Cadima, Jorge (2016-04-13). "Principal component analysis: a review and recent developments". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 374 (2065): 20150202. Bibcode:2016RSPTA.37450202J. doi:10.1098/rsta.2015.0202. PMC 4792409. PMID 26953178.
- ^ Barnett, T. P. & R. Preisendorfer. (1987). "Origins and levels of monthly and seasonal forecast skill for United States surface air temperatures determined by canonical correlation analysis". Monthly Weather Review. 115 (9): 1825. Bibcode:1987MWRv..115.1825B. doi:10.1175/1520-0493(1987)115<1825:oaloma>2.0.co;2.
- ^ Hsu, Daniel; Kakade, Sham M.; Zhang, Tong (2008). A spectral algorithm for learning hidden markov models. arXiv:0811.4413. Bibcode:2008arXiv0811.4413H.
- ^ a b Markopoulos, Panos P.; Kundu, Sandipan; Chamadia, Shubham; Pados, Dimitris A. (15 August 2017). "Efficient L1-Norm Principal-Component Analysis via Bit Flipping". IEEE Transactions on Signal Processing. 65 (16): 4252–4264. arXiv:1610.01959. Bibcode:2017ITSP...65.4252M. doi:10.1109/TSP.2017.2708023. S2CID 7931130.
- ^ a b Chachlakis, Dimitris G.; Prater-Bennette, Ashley; Markopoulos, Panos P. (22 November 2019). "L1-norm Tucker Tensor Decomposition". IEEE Access. 7: 178454–178465. arXiv:1904.06455. doi:10.1109/ACCESS.2019.2955134.
- ^ a b Markopoulos, Panos P.; Karystinos, George N.; Pados, Dimitris A. (October 2014). "Optimal Algorithms for L1-subspace Signal Processing". IEEE Transactions on Signal Processing. 62 (19): 5046–5058. arXiv:1405.6785. Bibcode:2014ITSP...62.5046M. doi:10.1109/TSP.2014.2338077. S2CID 1494171.
- ^ Zhan, J.; Vaswani, N. (2015). "Robust PCA With Partial Subspace Knowledge". IEEE Transactions on Signal Processing. 63 (13): 3332–3347. arXiv:1403.1591. Bibcode:2015ITSP...63.3332Z. doi:10.1109/tsp.2015.2421485. S2CID 1516440.
- ^ Kanade, T.; Ke, Qifa (June 2005). "Robust L₁ Norm Factorization in the Presence of Outliers and Missing Data by Alternative Convex Programming". 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Vol. 1. IEEE. pp. 739–746. CiteSeerX 10.1.1.63.4605. doi:10.1109/CVPR.2005.309. ISBN 978-0-7695-2372-9. S2CID 17144854.
- ^ Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space". Philosophical Magazine. 2 (11): 559–572. doi:10.1080/14786440109462720. S2CID 125037489.
- ^ Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417–441, and 498–520.
Hotelling, H (1936). "Relations between two sets of variates". Biometrika. 28 (3/4): 321–377. doi:10.2307/2333955. JSTOR 2333955. - ^ Stewart, G. W. (1993). "On the early history of the singular value decomposition". SIAM Review. 35 (4): 551–566. doi:10.1137/1035134. hdl:1903/566.
- ^ a b c d e Jolliffe, I. T. (2002). Principal Component Analysis. Springer Series in Statistics. New York: Springer-Verlag. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- ^ Bengio, Y.; et al. (2013). "Representation Learning: A Review and New Perspectives". IEEE Transactions on Pattern Analysis and Machine Intelligence. 35 (8): 1798–1828. arXiv:1206.5538. doi:10.1109/TPAMI.2013.50. PMID 23787338. S2CID 393948.
- ^ Forkman J., Josse, J., Piepho, H. P. (2019). "Hypothesis tests for principal component analysis when variables are standardized". Journal of Agricultural, Biological, and Environmental Statistics. 24 (2): 289–308. doi:10.1007/s13253-019-00355-5.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Boyd, Stephen; Vandenberghe, Lieven (2004-03-08). Convex Optimization. Cambridge University Press. doi:10.1017/cbo9780511804441. ISBN 978-0-521-83378-3.
- ^ A. A. Miranda, Y. A. Le Borgne, and G. Bontempi. New Routes from Minimal Approximation Error to Principal Components, Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer
- ^ Fukunaga, Keinosuke (1990). Introduction to Statistical Pattern Recognition. Elsevier. ISBN 978-0-12-269851-4.
- ^ Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). "Measuring systematic changes in invasive cancer cell shape using Zernike moments". Integrative Biology. 8 (11): 1183–1193. doi:10.1039/C6IB00100A. PMID 27735002.
- ^ Leznik, M; Tofallis, C. 2005 Estimating Invariant Principal Components Using Diagonal Regression.
- ^ Jonathon Shlens, A Tutorial on Principal Component Analysis.
- ^ a b c Soummer, Rémi; Pueyo, Laurent; Larkin, James (2012). "Detection and Characterization of Exoplanets and Disks Using Projections on Karhunen-Loève Eigenimages". The Astrophysical Journal Letters. 755 (2): L28. arXiv:1207.4197. Bibcode:2012ApJ...755L..28S. doi:10.1088/2041-8205/755/2/L28. S2CID 51088743.
- ^ Pueyo, Laurent (2016). "Detection and Characterization of Exoplanets using Projections on Karhunen Loeve Eigenimages: Forward Modeling". The Astrophysical Journal. 824 (2): 117. arXiv:1604.06097. Bibcode:2016ApJ...824..117P. doi:10.3847/0004-637X/824/2/117. S2CID 118349503.
- ^ a b Blanton, Michael R.; Roweis, Sam (2007). "K-corrections and filter transformations in the ultraviolet, optical, and near infrared". The Astronomical Journal. 133 (2): 734–754. arXiv:astro-ph/0606170. Bibcode:2007AJ....133..734B. doi:10.1086/510127. S2CID 18561804.
- ^ a b c Zhu, Guangtun B. (2016-12-19). "Nonnegative Matrix Factorization (NMF) with Heteroscedastic Uncertainties and Missing data". arXiv:1612.06037 [astro-ph.IM].
- ^ a b c d e f Ren, Bin; Pueyo, Laurent; Zhu, Guangtun B.; Duchêne, Gaspard (2018). "Non-negative Matrix Factorization: Robust Extraction of Extended Structures". The Astrophysical Journal. 852 (2): 104. arXiv:1712.10317. Bibcode:2018ApJ...852..104R. doi:10.3847/1538-4357/aaa1f2. S2CID 3966513.
- ^ "What are the Pros and cons of the PCA?". i2tutorials. September 1, 2019. Retrieved June 4, 2021.
- ^ Abbott, Dean (May 2014). Applied Predictive Analytics. Wiley. ISBN 9781118727966.
- ^ a b Jiang, Hong; Eskridge, Kent M. (2000). "Bias in Principal Components Analysis Due to Correlated Observations". Conference on Applied Statistics in Agriculture. doi:10.4148/2475-7772.1247. ISSN 2475-7772.
- ^ Linsker, Ralph (March 1988). "Self-organization in a perceptual network". IEEE Computer. 21 (3): 105–117. doi:10.1109/2.36. S2CID 1527671.
- ^ Deco & Obradovic (1996). An Information-Theoretic Approach to Neural Computing. New York, NY: Springer. ISBN 9781461240167.
- ^ Plumbley, Mark (1991). Information theory and unsupervised neural networks.Tech Note
- ^ Geiger, Bernhard; Kubin, Gernot (January 2013). "Signal Enhancement as Minimization of Relevant Information Loss". Proc. ITG Conf. On Systems, Communication and Coding. arXiv:1205.6935. Bibcode:2012arXiv1205.6935G.
- ^ See also the tutorial here
- ^ "Engineering Statistics Handbook Section 6.5.5.2". Retrieved 19 January 2015.
- ^ A.A. Miranda, Y.-A. Le Borgne, and G. Bontempi. New Routes from Minimal Approximation Error to Principal Components, Volume 27, Number 3 / June, 2008, Neural Processing Letters, Springer
- ^ Abdi. H. & Williams, L.J. (2010). "Principal component analysis". Wiley Interdisciplinary Reviews: Computational Statistics. 2 (4): 433–459. arXiv:1108.4372. doi:10.1002/wics.101. S2CID 122379222.
- ^ "SAS/STAT(R) 9.3 User's Guide".
- ^ eig function Matlab documentation
- ^ "Face Recognition System-PCA based". www.mathworks.com. 19 June 2023.
- ^ Eigenvalues function Mathematica documentation
- ^ Roweis, Sam. "EM Algorithms for PCA and SPCA." Advances in Neural Information Processing Systems. Ed. Michael I. Jordan, Michael J. Kearns, and Sara A. Solla The MIT Press, 1998.
- ^ Geladi, Paul; Kowalski, Bruce (1986). "Partial Least Squares Regression:A Tutorial". Analytica Chimica Acta. 185: 1–17. doi:10.1016/0003-2670(86)80028-9.
- ^ Kramer, R. (1998). Chemometric Techniques for Quantitative Analysis. New York: CRC Press. ISBN 9780203909805.
- ^ Andrecut, M. (2009). "Parallel GPU Implementation of Iterative PCA Algorithms". Journal of Computational Biology. 16 (11): 1593–1599. arXiv:0811.1081. doi:10.1089/cmb.2008.0221. PMID 19772385. S2CID 1362603.
- ^ Warmuth, M. K.; Kuzmin, D. (2008). "Randomized online PCA algorithms with regret bounds that are logarithmic in the dimension" (PDF). Journal of Machine Learning Research. 9: 2287–2320.
- ^ Kaplan, R.M., & Saccuzzo, D.P. (2010). Psychological Testing: Principles, Applications, and Issues. (8th ed.). Belmont, CA: Wadsworth, Cengage Learning.
- ^ Shevky, Eshref; Williams, Marilyn (1949). The Social Areas of Los Angeles: Analysis and Typology. University of California Press.
- ^ Flood, J (2000). Sydney divided: factorial ecology revisited. Paper to the APA Conference 2000, Melbourne, November and to the 24th ANZRSAI Conference, Hobart, December 2000.[1]
- ^ "Socio-Economic Indexes for Areas". Australian Bureau of Statistics. 2011. Retrieved 2022-05-05.
- ^ Human Development Reports. "Human Development Index". United Nations Development Programme. Retrieved 2022-05-06.
- ^ Novembre, John; Stephens, Matthew (2008). "Interpreting principal component analyses of spatial population genetic variation". Nat Genet. 40 (5): 646–49. doi:10.1038/ng.139. PMC 3989108. PMID 18425127.
- ^ Elhaik, Eran (2022). "Principal Component Analyses (PCA)‑based findings in population genetic studies are highly biased and must be reevaluated". Scientific Reports. 12 (1). 14683. Bibcode:2022NatSR..1214683E. doi:10.1038/s41598-022-14395-4. PMC 9424212. PMID 36038559. S2CID 251932226.
- ^ DeSarbo, Wayne; Hausmann, Robert; Kukitz, Jeffrey (2007). "Restricted principal components analysis for marketing research". Journal of Marketing in Management. 2: 305–328 – via Researchgate.
- ^ Dutton, William H; Blank, Grant (2013). Cultures of the Internet: The Internet in Britain (PDF). Oxford Internet Institute. p. 6.
- ^ Flood, Joe (2008). "Multinomial Analysis for Housing Careers Survey". Paper to the European Network for Housing Research Conference, Dublin. Retrieved 6 May 2022.
- ^ a b See Ch. 9 in Michael B. Miller (2013). Mathematics and Statistics for Financial Risk Management, 2nd Edition. Wiley ISBN 978-1-118-75029-2
- ^ a b §9.7 in John Hull (2018). Risk Management and Financial Institutions, 5th Edition. Wiley. ISBN 1119448115
- ^ §III.A.3.7.2 in Carol Alexander and Elizabeth Sheedy, eds. (2004). The Professional Risk Managers’ Handbook. PRMIA. ISBN 978-0976609704
- ^ example decomposition, John Hull
- ^ Libin Yang. An Application of Principal Component Analysis to Stock Portfolio Management. Department of Economics and Finance, University of Canterbury, January 2015.
- ^ Giorgia Pasini (2017); Principal Component Analysis for Stock Portfolio Management. International Journal of Pure and Applied Mathematics. Volume 115 No. 1 2017, 153–167
- ^ a b See Ch. 25 § "Scenario testing using principal component analysis" in Li Ong (2014). "A Guide to IMF Stress Testing Methods and Models", International Monetary Fund
- ^ Chapin, John; Nicolelis, Miguel (1999). "Principal component analysis of neuronal ensemble activity reveals multidimensional somatosensory representations". Journal of Neuroscience Methods. 94 (1): 121–140. doi:10.1016/S0165-0270(99)00130-2. PMID 10638820. S2CID 17786731.
- ^ Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000).
- ^ Jirsa, Victor; Friedrich, R; Haken, Herman; Kelso, Scott (1994). "A theoretical model of phase transitions in the human brain". Biological Cybernetics. 71 (1): 27–35. doi:10.1007/bf00198909. PMID 8054384. S2CID 5155075.
- ^ Benzécri, J.-P. (1973). L'Analyse des Données. Volume II. L'Analyse des Correspondances. Paris, France: Dunod.
- ^ Greenacre, Michael (1983). Theory and Applications of Correspondence Analysis. London: Academic Press. ISBN 978-0-12-299050-2.
- ^ Le Roux; Brigitte and Henry Rouanet (2004). Geometric Data Analysis, From Correspondence Analysis to Structured Data Analysis. Dordrecht: Kluwer. ISBN 9781402022357.
- ^ Timothy A. Brown. Confirmatory Factor Analysis for Applied Research Methodology in the social sciences. Guilford Press, 2006
- ^ Meglen, R.R. (1991). "Examining Large Databases: A Chemometric Approach Using Principal Component Analysis". Journal of Chemometrics. 5 (3): 163–179. doi:10.1002/cem.1180050305. S2CID 120886184.
- ^ H. Zha; C. Ding; M. Gu; X. He; H.D. Simon (Dec 2001). "Spectral Relaxation for K-means Clustering" (PDF). Neural Information Processing Systems Vol.14 (NIPS 2001): 1057–1064.
- ^ Chris Ding; Xiaofeng He (July 2004). "K-means Clustering via Principal Component Analysis" (PDF). Proc. Of Int'l Conf. Machine Learning (ICML 2004): 225–232.
- ^ Drineas, P.; A. Frieze; R. Kannan; S. Vempala; V. Vinay (2004). "Clustering large graphs via the singular value decomposition" (PDF). Machine Learning. 56 (1–3): 9–33. doi:10.1023/b:mach.0000033113.59016.96. S2CID 5892850. Retrieved 2012-08-02.
- ^ Cohen, M.; S. Elder; C. Musco; C. Musco; M. Persu (2014). Dimensionality reduction for k-means clustering and low rank approximation (Appendix B). arXiv:1410.6801. Bibcode:2014arXiv1410.6801C.
- ^ Hui Zou; Trevor Hastie; Robert Tibshirani (2006). "Sparse principal component analysis" (PDF). Journal of Computational and Graphical Statistics. 15 (2): 262–286. CiteSeerX 10.1.1.62.580. doi:10.1198/106186006x113430. S2CID 5730904.
- ^ Alexandre d'Aspremont; Laurent El Ghaoui; Michael I. Jordan; Gert R. G. Lanckriet (2007). "A Direct Formulation for Sparse PCA Using Semidefinite Programming" (PDF). SIAM Review. 49 (3): 434–448. arXiv:cs/0406021. doi:10.1137/050645506. S2CID 5490061.
- ^ Michel Journee; Yurii Nesterov; Peter Richtarik; Rodolphe Sepulchre (2010). "Generalized Power Method for Sparse Principal Component Analysis" (PDF). Journal of Machine Learning Research. 11: 517–553. arXiv:0811.4724. Bibcode:2008arXiv0811.4724J. CORE Discussion Paper 2008/70.
- ^ Peter Richtarik; Martin Takac; S. Damla Ahipasaoglu (2012). "Alternating Maximization: Unifying Framework for 8 Sparse PCA Formulations and Efficient Parallel Codes". arXiv:1212.4137 [stat.ML].
- ^ Baback Moghaddam; Yair Weiss; Shai Avidan (2005). "Spectral Bounds for Sparse PCA: Exact and Greedy Algorithms" (PDF). Advances in Neural Information Processing Systems. Vol. 18. MIT Press.
- ^ Yue Guan; Jennifer Dy (2009). "Sparse Probabilistic Principal Component Analysis" (PDF). Journal of Machine Learning Research Workshop and Conference Proceedings. 5: 185.
- ^ Hui Zou; Lingzhou Xue (2018). "A Selective Overview of Sparse Principal Component Analysis". Proceedings of the IEEE. 106 (8): 1311–1320. doi:10.1109/JPROC.2018.2846588.
- ^ A. N. Gorban, A. Y. Zinovyev, "Principal Graphs and Manifolds", In: Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods and Techniques, Olivas E.S. et al Eds. Information Science Reference, IGI Global: Hershey, PA, USA, 2009. 28–59.
- ^ Wang, Y.; Klijn, J. G.; Zhang, Y.; Sieuwerts, A. M.; Look, M. P.; Yang, F.; Talantov, D.; Timmermans, M.; Meijer-van Gelder, M. E.; Yu, J.; et al. (2005). "Gene expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer". The Lancet. 365 (9460): 671–679. doi:10.1016/S0140-6736(05)17947-1. PMID 15721472. S2CID 16358549. Data online
- ^ Zinovyev, A. "ViDaExpert – Multidimensional Data Visualization Tool". Institut Curie. Paris. (free for non-commercial use)
- ^ Hastie, T.; Stuetzle, W. (June 1989). "Principal Curves" (PDF). Journal of the American Statistical Association. 84 (406): 502–506. doi:10.1080/01621459.1989.10478797.
- ^ A.N. Gorban, B. Kegl, D.C. Wunsch, A. Zinovyev (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007. ISBN 978-3-540-73749-0
- ^ Vasilescu, M.A.O.; Terzopoulos, D. (2003). Multilinear Subspace Analysis of Image Ensembles (PDF). Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03). Madison, WI.
- ^ Vasilescu, M.A.O.; Terzopoulos, D. (2002). Multilinear Analysis of Image Ensembles: TensorFaces (PDF). Lecture Notes in Computer Science 2350; (Presented at Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark). Springer, Berlin, Heidelberg. doi:10.1007/3-540-47969-4_30. ISBN 978-3-540-43745-1.
- ^ Vasilescu, M.A.O.; Terzopoulos, D. (June 2005). Multilinear Independent Component Analysis (PDF). Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’05). Vol. 1. San Diego, CA. pp. 547–553.
- ^ Kriegel, H. P.; Kröger, P.; Schubert, E.; Zimek, A. (2008). "A General Framework for Increasing the Robustness of PCA-Based Correlation Clustering Algorithms". Scientific and Statistical Database Management. Lecture Notes in Computer Science. Vol. 5069. pp. 418–435. CiteSeerX 10.1.1.144.4864. doi:10.1007/978-3-540-69497-7_27. ISBN 978-3-540-69476-2.
- ^ Emmanuel J. Candes; Xiaodong Li; Yi Ma; John Wright (2011). "Robust Principal Component Analysis?". Journal of the ACM. 58 (3): 11. arXiv:0912.3599. doi:10.1145/1970392.1970395. S2CID 7128002.
- ^ T. Bouwmans; E. Zahzah (2014). "Robust PCA via Principal Component Pursuit: A Review for a Comparative Evaluation in Video Surveillance". Computer Vision and Image Understanding. 122: 22–34. doi:10.1016/j.cviu.2013.11.009.
- ^ T. Bouwmans; A. Sobral; S. Javed; S. Jung; E. Zahzah (2015). "Decomposition into Low-rank plus Additive Matrices for Background/Foreground Separation: A Review for a Comparative Evaluation with a Large-Scale Dataset". Computer Science Review. 23: 1–71. arXiv:1511.01245. Bibcode:2015arXiv151101245B. doi:10.1016/j.cosrev.2016.11.001. S2CID 10420698.
- ^ Liao, J. C.; Boscolo, R.; Yang, Y.-L.; Tran, L. M.; Sabatti, C.; Roychowdhury, V. P. (2003). "Network component analysis: Reconstruction of regulatory signals in biological systems". Proceedings of the National Academy of Sciences. 100 (26): 15522–15527. Bibcode:2003PNAS..10015522L. doi:10.1073/pnas.2136632100. PMC 307600. PMID 14673099.
- ^ Liao, T.; Jombart, S.; Devillard, F.; Balloux (2010). "Discriminant analysis of principal components: a new method for the analysis of genetically structured populations". BMC Genetics. 11: 11:94. doi:10.1186/1471-2156-11-94. PMC 2973851. PMID 20950446.
- ^ Jewson, S. (2020). "An Alternative to PCA for Estimating Dominant Patterns of Climate Variability and Extremes, with Application to U.S. and China Seasonal Rainfall". Atmosphere. 11 (4): 354. Bibcode:2020Atmos..11..354J. doi:10.3390/atmos11040354.
- ^ Scher, S.; Jewson, S.; Messori, G. (2021). "Robust Worst-Case Scenarios from Ensemble Forecasts". Weather and Forecasting. 36 (4): 1357–1373. Bibcode:2021WtFor..36.1357S. doi:10.1175/WAF-D-20-0219.1. S2CID 236300040.
- ^ Jewson, S.; Messori, G.; Barbato, G.; Mercogliano, P.; Mysiak, J.; Sassi, M. (2022). "Developing Representative Impact Scenarios From Climate Projection Ensembles, With Application to UKCP18 and EURO-CORDEX Precipitation". Journal of Advances in Modeling Earth Systems. 15 (1). doi:10.1029/2022MS003038. S2CID 254965361.
- ^ "Principal Components Analysis". Institute for Digital Research and Education. UCLA. Retrieved 29 May 2018.
Further reading
[edit]- Jackson, J.E. (1991). A User's Guide to Principal Components (Wiley).
- Jolliffe, I. T. (1986). Principal Component Analysis. Springer Series in Statistics. Springer-Verlag. pp. 487. CiteSeerX 10.1.1.149.8828. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- Jolliffe, I. T. (2002). Principal Component Analysis. Springer Series in Statistics. New York: Springer-Verlag. doi:10.1007/b98835. ISBN 978-0-387-95442-4.
- Husson François, Lê Sébastien & Pagès Jérôme (2009). Exploratory Multivariate Analysis by Example Using R. Chapman & Hall/CRC The R Series, London. 224p. ISBN 978-2-7535-0938-2
- Pagès Jérôme (2014). Multiple Factor Analysis by Example Using R. Chapman & Hall/CRC The R Series London 272 p
External links
[edit]- University of Copenhagen video by Rasmus Bro on YouTube
- Stanford University video by Andrew Ng on YouTube
- A Tutorial on Principal Component Analysis
- A layman's introduction to principal component analysis on YouTube (a video of less than 100 seconds.)
- StatQuest: StatQuest: Principal Component Analysis (PCA), Step-by-Step on YouTube
- See also the list of Software implementations



































![{\displaystyle \mathbf {X} =[X_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4daaf2305609bbd2142de16bbb6cb774218d22)






![{\displaystyle \mathbf {u} =[u_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95df093fae62b2ab6dfa4527c69d1cbd3b9d553f)

![{\displaystyle \mathbf {s} =[s_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf19191b22b96e131d03b5b3d1ce7dde1cc877ba)
![{\displaystyle \mathbf {h} =[h_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0ef2db0dd2d098b4893574eca8b44d04fde0653)

![{\displaystyle \mathbf {B} =[B_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c8b8dd810252420486677821841d9c24c7cf58d)
![{\displaystyle \mathbf {Z} =[Z_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/924bacc6ac643a5165b78f62aa36ec85f3e94cd8)
![{\displaystyle \mathbf {C} =[C_{jj'}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1652c6b60c22140c190acfa8f49084ccc4ca8f9c)


![{\displaystyle \mathbf {R} =[R_{jj'}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecc703ef34aa1c05d4b86462435d9eef3dbadde)
![{\displaystyle \mathbf {V} =[V_{jj'}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebedde6d7a291b8a304447f9467f85c6325d4755)
![{\displaystyle \mathbf {D} =[D_{jj'}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5a835ec95447679384c75da973ebdb23fcb0d56)

![{\displaystyle \mathbf {W} =[W_{jl}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95c3a7bd748ee5e1b0ebbddc41e61fa6d16d26a5)


![{\displaystyle \mathbf {T} =[T_{il}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/684b2536b0cdea539fc13d7d4b92b40557727609)
















































![{\displaystyle {\begin{aligned}\operatorname {cov} (PX)&=\operatorname {E} [PX~(PX)^{*}]\\&=\operatorname {E} [PX~X^{*}P^{*}]\\&=P\operatorname {E} [XX^{*}]P^{*}\\&=P\operatorname {cov} (X)P^{-1}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e4800248eafcc33b2c22c5613f06b0c2455faad)





